抛物非球面零位干涉检测的补偿器设计
闫钧华,胡子佳,朱德燕,陈 阳,张 寅,范君杰
(1.南京航空航天大学空间光电探测与感知工业和信息化部重点实验室,江苏南京 211106;2.南京航空航天大学航天学院,江苏南京 211106)
与球面相比,非球面在光学系统中有扩大视场角度、减少系统能量损失、透光性好、简化系统等优点[1]。随着国家航天技术的进步,光电探测、地面遥感等领域对光学系统更高的要求,基于非球面的光学系统在航天领域具有普遍而重要的应用,例如导弹的共形光学系统、飞行器的光电载荷系统等[2]。光电载荷作为无人机的“眼睛”需要清晰地完成对空中的侦查、测量等任务,以便快速提供精准、可靠的信息。在光电载荷系统中,非球面作为核心部件起到了关键性的作用。
对非球面高精度的检测是加工高质量非球面的保障。当前,轮廓检测和干涉检测是非球面检测的主要手段。轮廓检测动态范围大,不需要辅助装置,操作简单,但检测精度低,不能满足高精度要求,干涉检测中子孔径拼接法精度较高,但检测时间长,对机械结构要求高而且数据处理复杂[3-5]。无像差点法精度高但有局限性,需要大的辅助镜且有中心遮拦[2]。零位干涉中的计算全息(Computer-Generated Hologram,CGH)检测精度高,检测速度快,但对于特定的非球面,特制的CGH 设计过程复杂[6-8]。零位干涉补偿检测法中常见的补偿器有Offner 型补偿器、Dall 型补偿器、反射镜补偿器等[9-11]。Offner 型补偿器无遮拦且没有彗差影响,检测精度高,可靠性强。
该文针对具体口径为800 mm,曲率半径为1 400 mm的抛物非球面,分析并设计了Offner 型补偿器结构。利用Zemax 软件对给定的抛物非球面进行优化,完成对非球面高精度的检测及公差分析。
1 待测非球面的光学特点
非球面的参数性质决定了补偿器的结构,非球面大多数情况下为旋转对称型,表达式如下:


图1 非球面几何性质图
在坐标系ZOY中固定非球面,非球面顶点在原点O上,OZ轴表示为光轴。在非球面上取一点b′,坐标为(z,y),C点为非球面法线b′C与光轴的交点,ϕ为非球面法线b′C与光轴间的倾角。根据非球面顶点O和交点C的位置得出顶点球面和最佳拟合球面的位置,在光轴上,C0点为顶点球面的曲率中心,R0为顶点球面的曲率半径,C1点为最佳拟合球面的曲率中心,非球面的法线分别与最佳拟合球面和顶点球面交于点b和b″。θ为b′C1与光轴间的倾角,δ为非球面法线b′C与b′C1的夹角。b′C0与b′C1在光轴上的距离X1为最佳拟合球面与顶点球面曲率中心的偏移量。Ln为非球面的轴向球差[12]。
计算公式如式(2)所示:
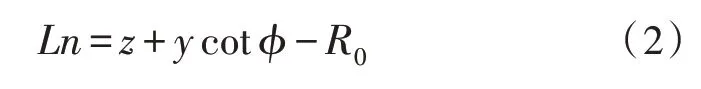
由解析几何求得:
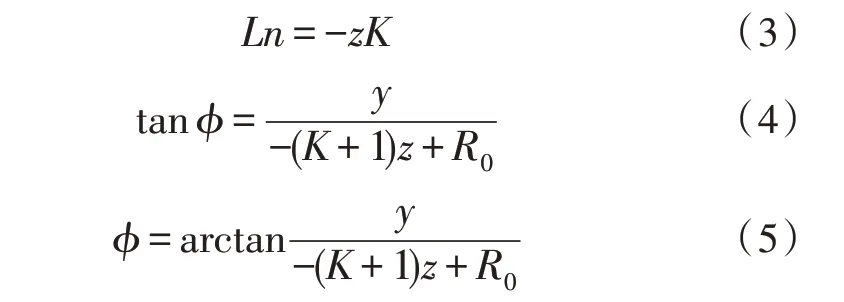
非球面与顶点球面在法线方向上的偏移量b′b″可以根据轴向球差Ln求解得到。需要选择一个最佳拟合球面,使非球面度即非球面表面与拟合球面的偏移量尽量小。最佳拟合球面与非球面法线方向上的偏移量为bb′,可以用非球面法线与光轴交点C与最佳拟合球面的曲率中心C1之间的距离CC1(CC1=Ln-X1)来表示[13]。根据几何光学中球差与波像差之间的关系有以下公式:
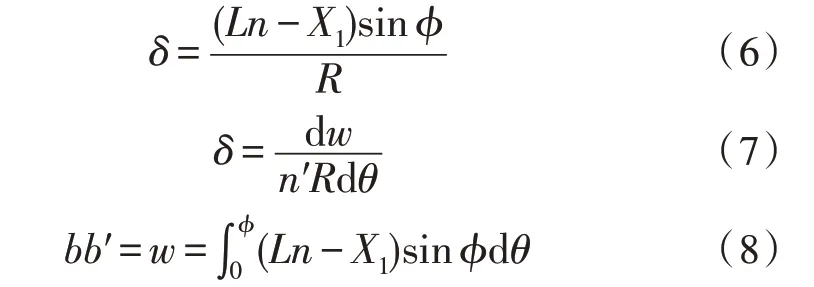
式(6)~(8)中,w为非球面度,从图1 可知θ=ϕ+δ,所 以有dθ=dϕ+dδ。令R≈R0,,对于抛物面,K=-1,可得式(9):
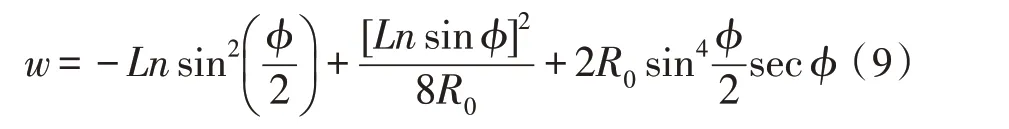
该文需要检测的非球面的各项参数如表1所示。

表1 非球面参数
根据表1的非球面的参数和式(1)~(9)得出:非球面的非球面度曲线如图2 所示,非球面与最佳拟合球曲线切线的斜率(非球面梯度曲线)如图3所示。
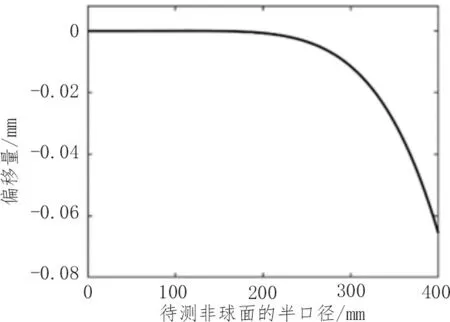
图2 非球面度曲线
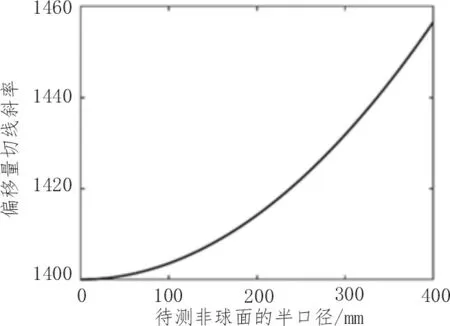
图3 非球面梯度曲线
2 Offner型补偿器的设计
非球面检测的难易程度由非球面梯度曲线反映,该斜率值的最大值反映了难度大小。针对该结构特点,采用Offner 型补偿器,干涉仪所用的波长为632.8 nm,发出的球面波前经过补偿镜和场镜,将转换的与非球面匹配的非球面波前成像在非球面上,被非球面反射回干涉仪,与标准波前进行干涉,可以由干涉图像获得非球面的全口径信息[11],设计图如图4 所示。
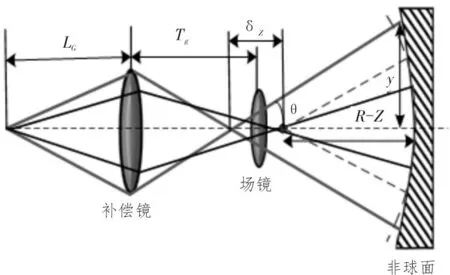
图4 Offner补偿器设计图
2.1 Offner型补偿器参数的计算
设计的补偿器需要产生刚好与非球面所带的球差相抵消的球差。以反射抛物非球面为例,整体放大率为-1,由被检测的非球面所产生的轴向球面像差W040A表示为[14-15]:
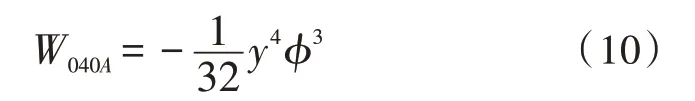
式(10)中,y为非球面的半口径,ϕ为光焦度,法线像差表示如式(11)所示:

按照图4 所示原理图求得Offner 补偿器初始结构。y是补偿镜口径的一半,Tg是补偿镜与场镜之间的距离,R为曲率半径,yG、fG、LG分别是补偿镜的半口径、焦距和距离物点的距离,计算公式如式(12)~(14)所示:
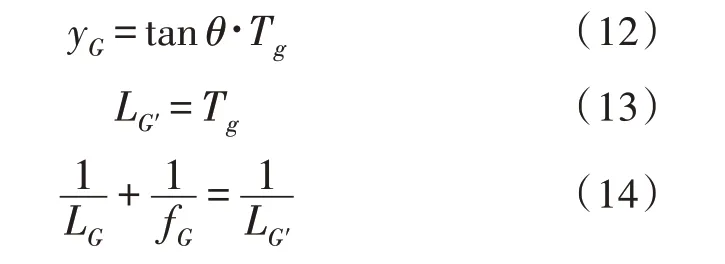
求得补偿镜的焦距fG后即可求曲率半径,计算公式如式(15)和式(16):
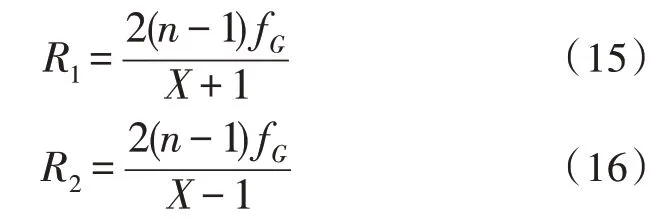
式(15)~(16)中,X为形状因子,对于平凸透镜,当平面对着光源时,X=-1;当凸面对着光源时,X=1;对于双凸透镜,则X=0。
2.2 利用Zemax构建Offner型补偿器
针对给定的曲率半径1 400 mm,口径为800 mm的抛物非球面,首先采用逆向设计,建立折射率为0的虚拟玻璃。在设计补偿器的过程中,关键问题是需要经过补偿器的波前可以刚好沿法线入射。提出建立虚拟玻璃的设计思路,根据Snell 折射定律,有式(17)的等式:
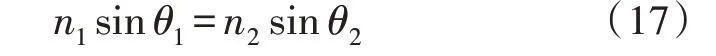
式(17)中折射介质的折射率n2不为0,以不同角度由介质射入到非球面的光线要沿着法线方向射出,意味着折射角θ2为0,从而等式右边为0。等式左边与等式右边需要相等,入射角度θ1不为0,因此入射介质n1为0。原理图如图5 所示。
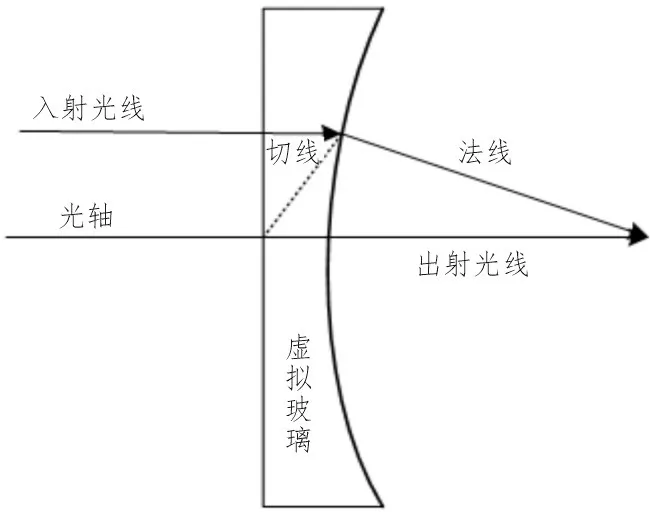
图5 玻璃原理图
在Zemax光学设计软件中自定义名字为ZERO的新的折射率为0的玻璃,然后根据式(10)~(16)计算得到轴向球差W040A为-2.332 mm,得出Offner 补偿器的结构参数,建立起单光路补偿器的初始结构。将曲率半径和厚度设为变量,以波像差为0 作为目标进行优化,得到单光路补偿器的设计,如图6 所示。由于光路可逆性原则,用Pickup 控制出射的光路与从非球面返回的光路曲率半径相同,厚度相同但为相反符号,设计出双光路检测系统即Offner 型补偿器,结构参数如表2 所示,Offner 型补偿器设计图如图7 所示。
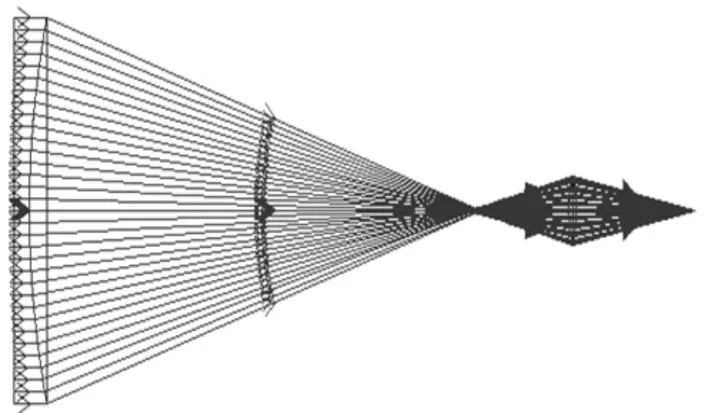
图6 单光路补偿器设计图
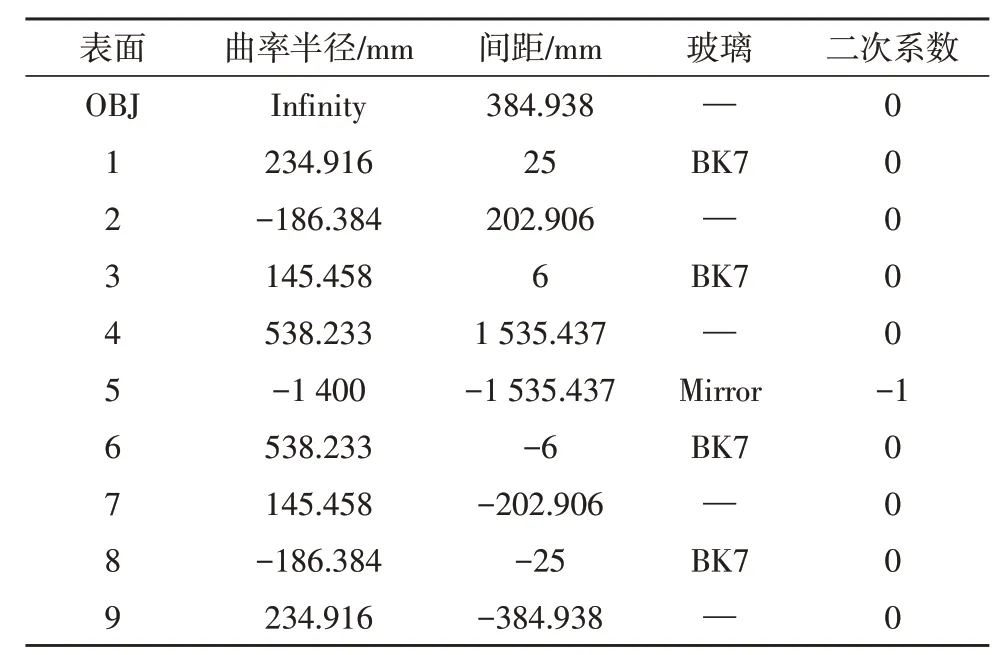
表2 Offner型补偿器设计结果

图7 Offner型补偿器设计图
非球面的反射波前与参考波前产生的干涉条纹如图8 所示,当被测非球面的像差能被补偿器补偿,存在面型误差小时,探测器得到的是直条纹。

图8 干涉图
非球面检测系统波像差为PV=0.014 8λ,RMS=0.003 6λ,如 图9所示,设计结果满足PV<0.25λ,RMS<0.02λ的高精度要求。
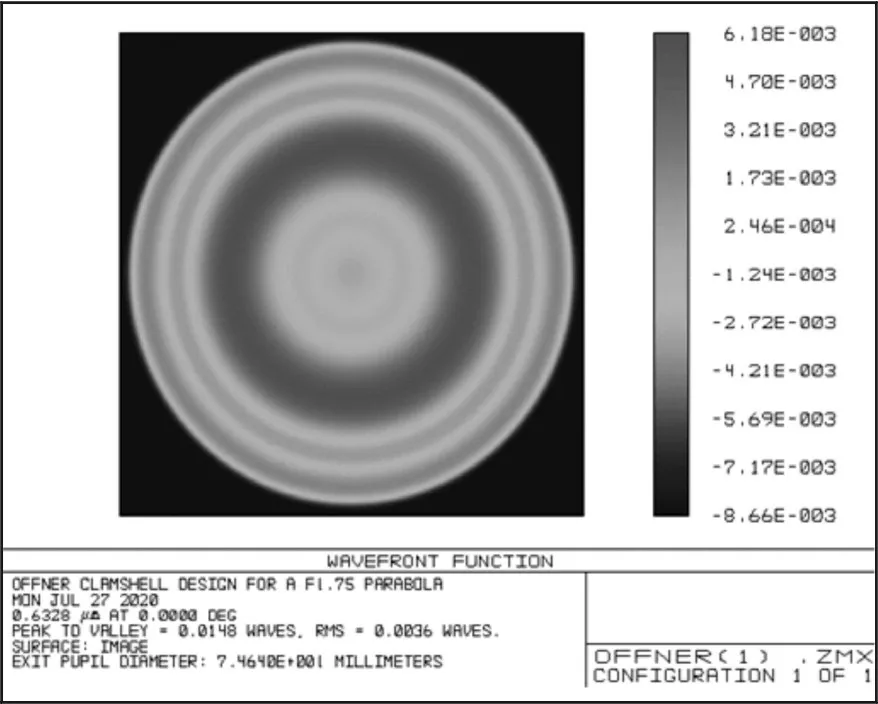
图9 Offner型补偿器检测设计残差
3 公差分析
公差分析可以得到补偿器在加工及其装配的过程中产生元件的厚度误差、元件的偏心误差等各种误差,从而提高补偿器的精度。由于检测系统波长为单色波长,所以阿贝数不需要考虑。系统采用均匀性好、折射率高的BK7 玻璃,从而提高波面质量。将场镜和补偿镜之间的距离、补偿器最后一面到被检测非球面之间的距离和后焦距作为公差的补偿[16]。各个参数的公差容限如表3 所示,表4 第二列为补偿器的结构数据,第三列为透镜曲率半径及厚度的加工误差,第四列为相应的波像差变化。

表3 结构参数的公差容限
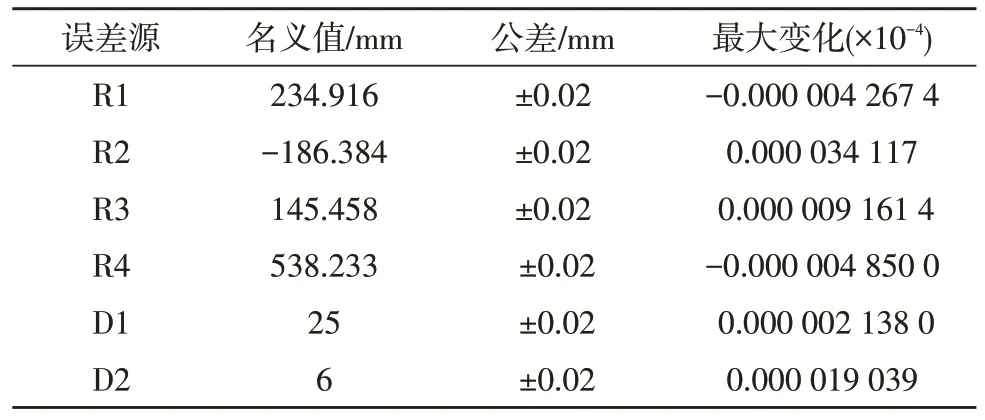
表4 部分结构公差预定值
如表5所示,蒙特卡罗分析[17]结果表明,模拟20次补偿器实际加工后,波前差有90%概率达到0.02λ。如果选择标准面误差RMS 小于0.01λ的干涉仪时,最后补偿器残留的波像差RMS 变化量约为:
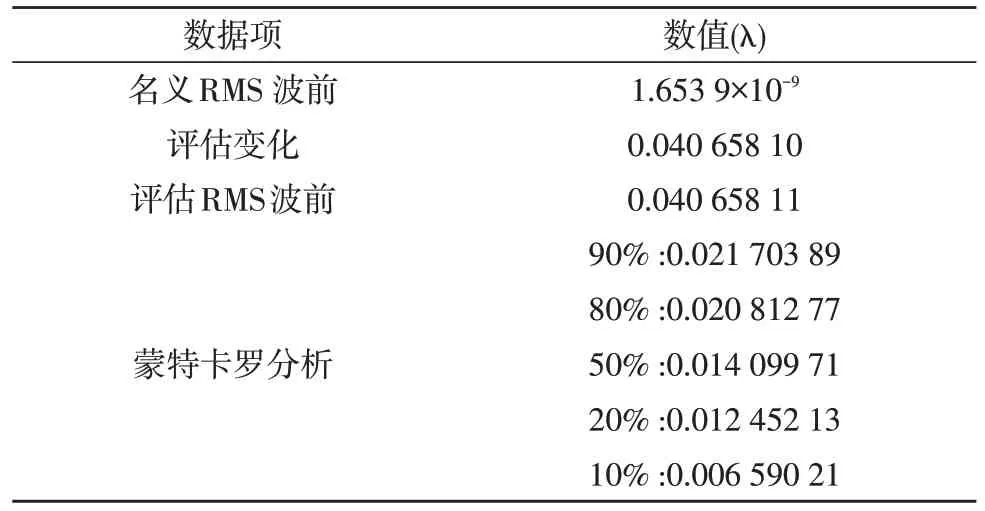
表5 公差分析结果
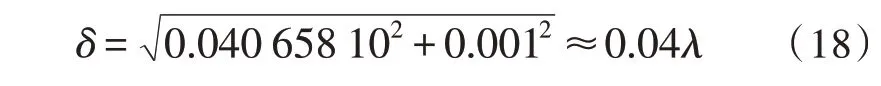
系统残留波像差约为:

被检镜表面为反射面,面形精度要求为0.02λ,在干涉测量时被放大两倍为0.04λ,所以补偿器精度满足要求。
4 结论
该文针对口径为800 mm,曲率半径为1 400 mm的抛物非球面,设计了零位干涉补偿器中的Offner型补偿器进行补偿。基于像差理论计算得到Offner型补偿器结构参数后,利用Zemax,采用逆向设计思路定义了折射率为0,命名为ZERO的虚拟玻璃,解决了光线沿法线方向出射的关键问题。优化所建立的初始结构,得到单光路补偿器。根据光路可逆性原则,得出了Offner 型补偿器检测系统。检测系统的设计 结果 为PV=0.014 8λ,RMS=0.003 6λ,达 到PV<0.25λ、RMS<0.02λ的高精度要求。最后进行公差分析,得到了补偿器结构的残余波像差,表明公差在合适的范围内,验证了设计的可行性。

