光学自由曲面面形检测技术

张 磊，刘 东，师 途，杨甬英，李劲松，俞本立

(1.安徽大学 光电信息获取与控制教育部重点实验室，安徽 合肥 230601; 2. 浙江大学 现代光学仪器国家重点实验室，浙江 杭州 310027)

光学自由曲面面形检测技术

张 磊1*，刘 东2，师 途2，杨甬英2，李劲松1，俞本立1

(1.安徽大学 光电信息获取与控制教育部重点实验室，安徽 合肥 230601; 2. 浙江大学 现代光学仪器国家重点实验室，浙江 杭州 310027)

光学自由曲面因其表面自由度较大，可以针对性地提供或矫正不同的轴上或轴外像差，同时满足现代光学系统高性能、轻量化和微型化的要求，逐渐成为现代光学工程领域的热点。自由曲面的检测技术已经成为制约其应用的最重要因素，而目前精密光学自由曲面的检测手段仍然沿用非球面检测方法。本文回顾了近年来的自由曲面检测发展历程，对目前主流的非接触式检测方法(微透镜阵列法，结构光三维检测法，相干层析术，干涉检测法)进行了重点介绍；总结了非球面检测方法运用到自由曲面检测中的技术难点，同时结合这些技术难点，展望了自由曲面检测的未来发展新趋势，主要集中在非旋转对称像差的动态补偿、分区域像差的回程误差校准及子孔径拼接技术。

自由曲面检测；干涉检测法；子孔径拼接；非旋转对称像差补偿

1 引 言

光学自由曲面元件其表面自由度较大，可以针对性地提供或矫正不同的轴上或轴外像差，同时满足现代光学系统高性能、轻量化和微型化的要求，逐渐成为现代光学研究领域和工业及商业领域的新宠。广义的光学自由曲面包括回转对称非球面和非回转对称非球面，狭义的光学自由曲面仅指非旋转对称非球面，其口径内各处曲率半径各不相同，很难在全口径内使用统一的数学方程描述[1]。自由曲面一般具有不规则形状，可以提供较高的像差自由度，或者复杂的光线出射方向以及照度分布，因此对于照明，显示和成像等领域具有极大的吸引力。自20世纪90年代起，照明和显示光学系统中已经开始采用自由曲面设计[2-5]，可以根据需求合理控制光线散射角度与光强分布。在成像光学系统中，自由曲面的应用刚刚起步，并不如显示和照明系统成熟，尤其对于一些高精度成像领域，仅在一些大型研究机构中才能出现自由曲面的身影，如美国航天局(NASA)研制的三反成像系统[6]。欧洲南方天文台超大望远镜中的光谱仪(VLT)中便采用了多块象散镜[7]。

目前成像光学系统中自由曲面应用主要包括离轴非球面、象散面、复曲面、柱面、Zernike曲面、微结构光学曲面等。其中离轴非球面主要用在各种离轴三反光学系统中；复曲面是指正交子午线对称，且在子午线上存在曲面曲率半径的最大值和最小值的曲面，可以在正交方向上提供不同的像差校正；象散面主要为光学系统提供不同方向的象散，例如VLT中便采用了多块象散镜；Zernike曲面是由不同形式的Zernike多项式描述并构造的曲面，现已被应用在离轴三反和高光谱成像系统中；微结构光学曲面主要是指微透镜阵列、菲涅尔透镜、全息透镜和微型V槽上的微结构曲面。

正是由于成像领域对于光学元件面形的高精度要求限制了自由曲面的大规模应用。在过去的几十年中，非球面的设计和加工检测均获得了长足进步，而自由曲面设计加工和检测发展则相对缓慢，尤其是自由曲面的检测技术已经成为制约其应用的最重要因素。本文针对适用于成像系统的面形连续变化自由曲面检测技术进行总结与分析，并根据其检测难点展望未来发展趋势。

2 精密光学自由曲面检测方法

自由曲面的检测方法主要分为接触式和非接触式[8]，其中接触式检测法采用逐点扫描的方式进行测量，其中具有代表性的是坐标测量机法(Coordinate Measurement Machine，CMM)和轮廓仪法[9]。目前CMM法由于测头容易造成被测光学元件表面划伤，不能一次性检测全口径面形误差，因而速度较慢，且单点数据经拼接后精度仅停留在微米量级，限制了其在成像自由曲面检测中的应用。轮廓仪法也仅能检测某一轮廓线的误差，不属于真正的自由曲面面形检测。经过抛光之后的光学自由曲面对测量的超高精度要求以及在检测过程中必须兼顾测量精度和测量范围之间的矛盾使得传统的接触式测量已经无法满足要求。受到非球面检测方法的启发，研究人员逐渐将各种非接触式非球面检测方法应用到自由曲面检测的研究中，并取得了一定的进展。目前受到广泛关注的光学自由曲面面形非接触式检测方法主要有微透镜阵列法、结构光三维测量法、相干层析法和干涉测量法，下面针对这几种典型检测方法进行相关介绍。

2.1 微透镜阵列法

微透镜阵列相较于传统单个透镜，可以将入射的被测波面分割为多个子波前区域，使得每个子波前区域的畸变在探测器的检测范围之内，进而重构整个被测波面。根据微透镜阵列在光学系统中不同的位置和不同的波前重构方法，目前的微透镜阵列自由曲面检测法可分为两大类：夏克-哈特曼波前探测法和倾斜波干涉仪法,其中倾斜波干涉仪法将在干涉检测的内容中详述，此处仅介绍夏克-哈特曼波前探测法。

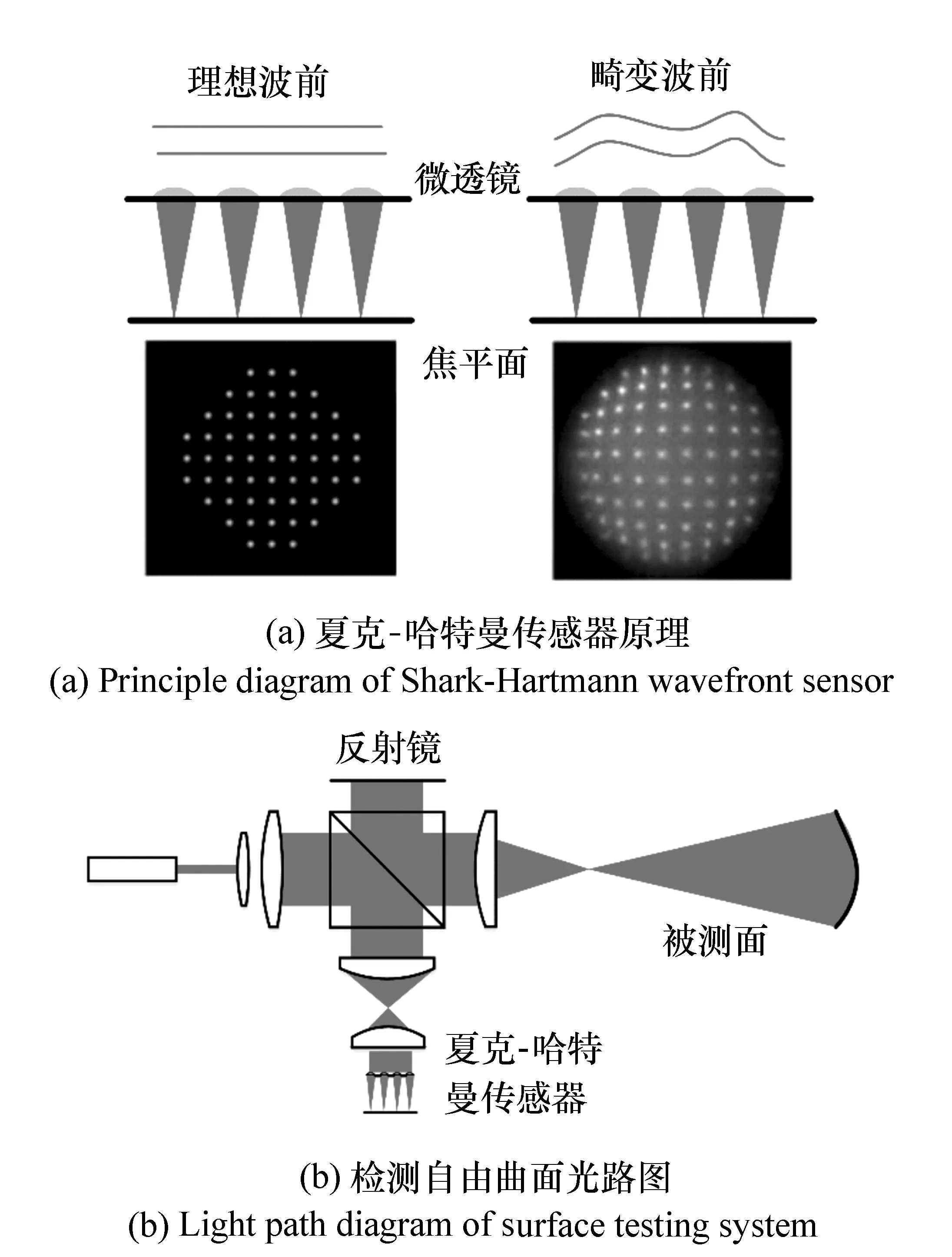
图1 夏克-哈特曼传感法检测自由曲面原理 Fig.1 Principle of Shark-Hartmann wavefront sensor in free-form surface test

夏克-哈特曼波前探测法是一种利用夏克-哈特曼波前传感器进行波前斜率测量的方法。夏克-哈特曼波前传感器主要由微透镜阵列和位于微透镜焦距处的CCD相机构成，其中微透镜阵列由上百个相同尺寸和相同焦距的微透镜按一定的规律紧密排列而成，其工作原理如图1(a)所示。在传感器中，用微透镜阵列将入射波前分割成许多子波前, 平面波入射时，像面上呈现均匀排列的光斑，当入射波前存在变形，则变形部分的子波前经对应微透镜后在像面的汇聚点将偏离理想像点，在全口径像面上形成非均匀光斑排列。探测被测波前的子波前光斑相对标定光斑的偏移量就能测量各个子孔径内波前在x和y方向上的子波前斜率，根据这些斜率数据经过波前复原算法即可以重构出被测波前的相位信息。图1(b)所示为夏克-哈特曼传感器检测自由曲面典型光路。该光学系统结构使得标准平面波前经被测自由曲面反射后，波前相位信息受到自由曲面面形调制，通过夏克哈特曼传感器重构受调制波前相位，即可反演出被测曲面面形。

20世纪末，桑迪亚国家实验室率先将夏克哈特曼探测器用来测量光学元件的面形误差[10]；2002年，Paul D.Pulaski[11]等人利用夏克哈特曼探测器对微透镜阵列进行了面形测量；2005年，美国罗彻斯特大学将夏克哈特曼探测器用于薄透镜和隐形眼镜等光学元件的测量[12]；2012年新加坡W．Guo等人[13]提出一种自适应光斑中心判定法，使得夏克哈特曼波前探测法在自由曲面面形检测中的精度达到了27 nm rms。国内天津大学[14]利用夏克哈特曼波前探测法检测口径2 mm的立方相位板，检测结果与Veeco白光干涉仪比对精度达到0.2%。

图2 夏克-哈特曼传感的检测限制 Fig.2 Testing limitation of Shark-Hartmann wavefront sensor

然而，夏克哈特曼波前探测法由于探测器接收面积有限，受到其微透镜阵列个数的限制，因采样率低获得的波前斜率数据有限，如图2所示，导致其横向分辨率不高；另外，其动态范围也受到微透镜尺寸限制，在对大曲率半径表面检测时像面光斑偏离过大，可能相互混叠，甚至会超出CCD成像范围，造成波前恢复错误。

2.2 结构光三维测量法

结构光三维测量法是采用不同类型的结构光投射至物体上，利用摄影系统采集自由曲面调制光图样；通过光场受调制情况推演光场相位或强度信息的变化，进而换算为被测面高度起伏信息，从而重构出被测面三维面形信息。结构光三维测量法种类繁多，按照投射光源的不同可分为点结构光法、线结构光法、编码结构光法以及面结构光法等。其中，仅有面结构光法可以一次性获得全场面形信息而受到广泛关注。面结构光三维测量方法[15-38]将面阵条纹图像投影至被测物，可实现全场的高精度测量，其中主流的方法包括条纹投影法和条纹反射法等[15]。二者基本原理一致，如图3所示。

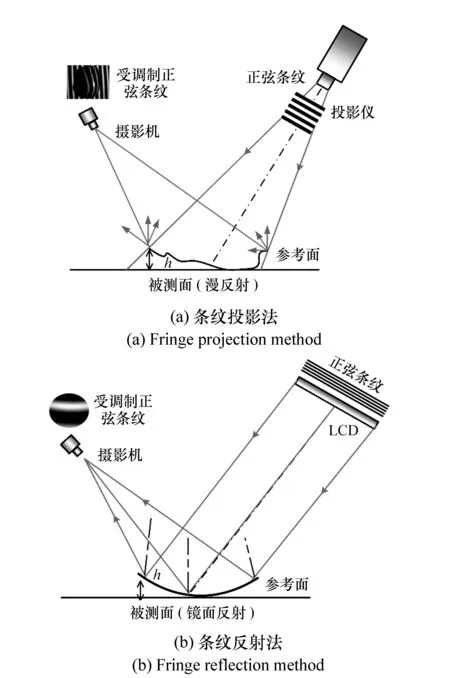
图3 面结构光三维检测基本原理 Fig.3 Principle of surface structured light 3D measurement

利用光栅投影或激光干涉产生高质量条纹(或计算机产生的标准正弦条纹)，将其投射至物体上，利用摄影系统采集收到自由曲面调制而变形的条纹图样，通过对受调制条纹图进行解调，解包裹等处理得到受调制相位分布；再通过相位和被测面起伏高度之间的数学关系将相位换算为被测面表面起伏梯度，进而通过数值积分得到被测面三维面形分布；二者的主要区别在于适用范围不同，条纹投影法适用于测量漫反射曲面，而条纹反射法则适用于测量镜面反射曲面。由图3可见条纹反射法仅能在被测曲面的镜面反射方向采集受调制条纹。

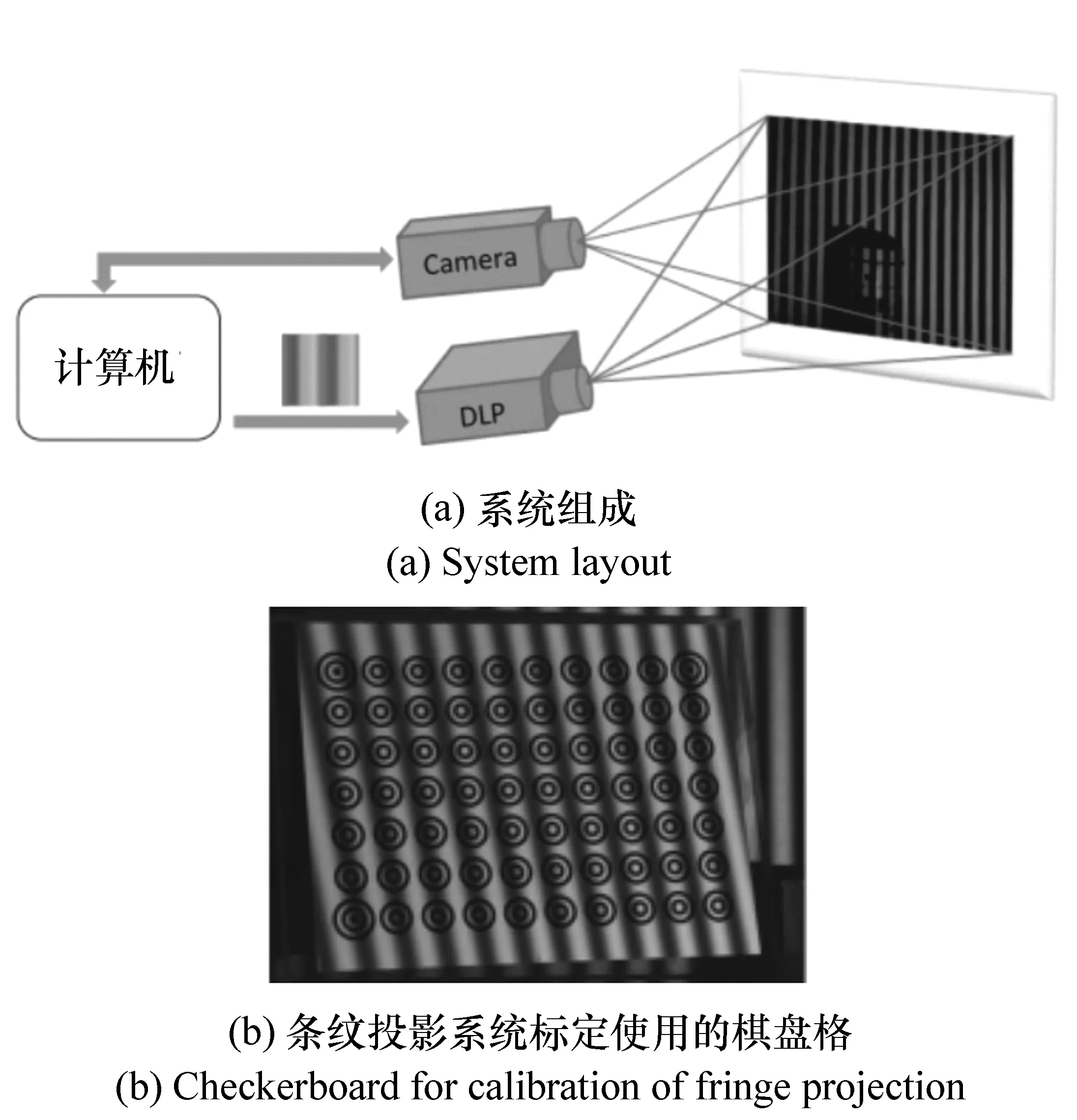
图4 美国Catholic大学条纹投影技术设备 Fig.4 Device of fringe projection in Catholic university

条纹投影三维形貌测量技术的研究和应用在国外比较成熟。目前的研究热点集中在系统标定、位相解调、相位高度转换算法上。美国Catholic大学Wang Zhaoyang教授团队[16-23]长期致力于利用该技术工业自由曲面实时测量研究，研制了高精度条纹投影重构设备，如图4(a)所示，提出了高精度的棋盘格加控制方程标定方法[19-20](图4(b))、高精度快速相位恢复方法[23]以及相位高度换算方法[17]，目前已经达到检测速度22.5 fps，相对检测精度0.01%[16]；哈佛大学S.Zhang和 P.S.Huang 等人[24-26]研制的条纹投影设备也已经达到了检测速度40 fps，相对检测精度0.025%。很多商业产品也陆续出现，代表国际先进水平的有德国的Gom公司开发的便携式Atos系列三维扫描仪[27-28],首创参考点拼合并应用先进的摄像机定位技术，在测量时候自动拼接，提高大型件的扫描精度。国内条纹投影三维形貌测量技术目前还处于起步阶段，一些高校和公司已经开始了这方面的研究。南京理工大学[29]使用改进的DLP投影仪和可编程控制电路板研制成功了集成条纹投影设备，达到速度120 fps，检测精度0.527%。1992年，四川大学开始该领域的研究，主要集中在改进投影产生和获取的方法以及改进条纹分析方法，目前检测精度达到1%(0.3 mm/33 mm)[30-31]。

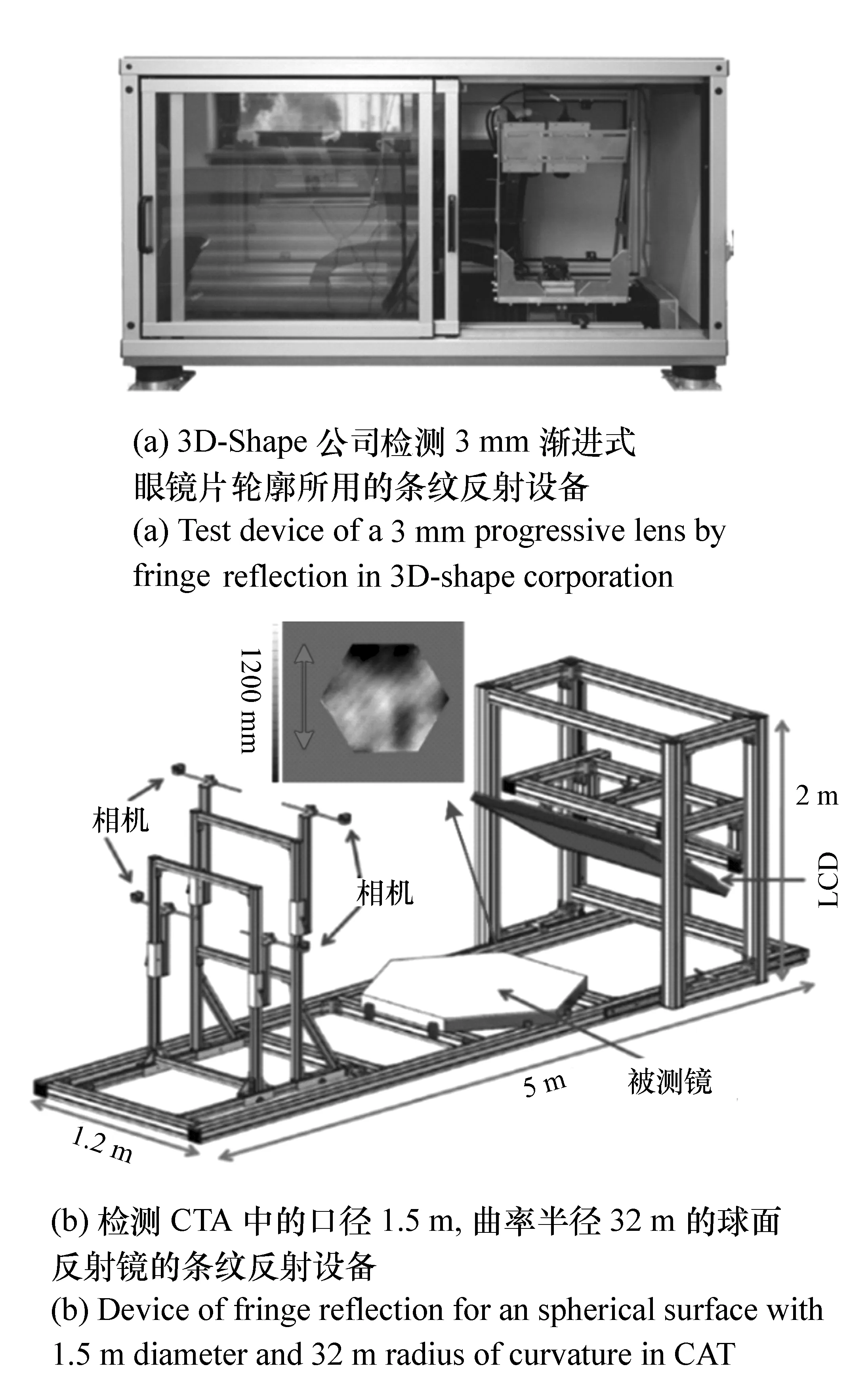
图5 条纹反射设备 Fig.5 Devices of fringe reflection

上述条纹技术均是针对一般的漫反射自由曲面进行检测。受其启发，人们利用条纹反射检测自由曲面光学元件轮廓的研究也未曾停步。尤其对于非球面和自由曲面光学元件的检测不需要任何光学补偿，使得众多科研工作者从传统干涉检测将目光转向了这一技术领域。德国3D-Shape公司利用条纹反射技术检测3 mm渐进式眼睛片轮廓已经达到20 nm精度[39](图5(a))。Krobot R等人利用该技术检测Cherenkov Telescope Array(CTA)中的口径1.5 m，曲率半径32 m的球面反射镜，精度达到10 μm(图5 (b))[32]。另外，美国Arizona大学[33]、德国Saarland大学[34]、新加坡南洋理工大学[35]、国内的清华大学[36-37]、四川大学[30]、中科院成都光电所[38]等单位也都对该技术进行了研究并取得一定成果,对非球面检测最高精度达到0.01%。目前对于真正意义上的光学自由曲面检测的报道依然很少，且基本处于实验室研究阶段。

2.3 相干层析技术

光学相干层析技术是利用当参考光脉冲和信号光的某个脉冲经过相等光程，同时到达探测器发生干涉。移动参考镜，使参考光脉冲与不同深度的信号光脉冲发生干涉，记录下相应的参考镜位置，便可反映被测样品不同的深度信息；另一方面，光束在样品表面做二维扫描得到横向信息，综合可得样品立体层析图像。目前将光学层析技术成功应用于自由曲面检测的典型是罗切斯特大学的扫频光学层析术(Swept source optical coherence tomography,SS-OCT)[40-42]，其检测结构为图6(a)所示的马赫曾德干涉结构，扫频激光经过分束后，一部分进入参考路，参考路中光栅用来补偿光源色散；一部分进入检测路的振镜扫描系统，完成对被测曲面的二维扫描。

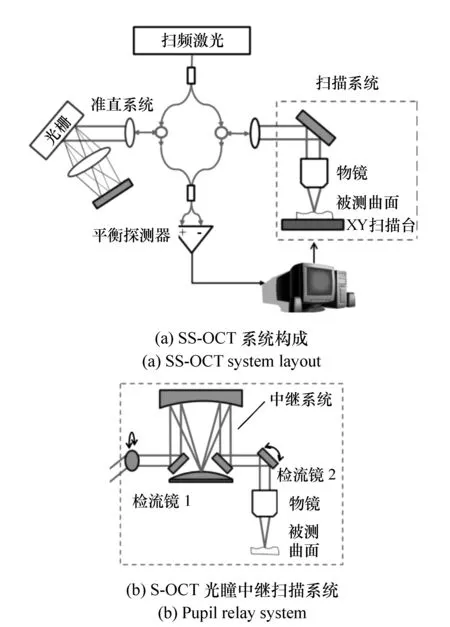
图6 SS-OCT系统原理 Fig.6 Principle diagram of SS-OCT system

图6(a)中所示扫描系统的xy机械平移台由于移动误差，难免造成获取的表面面形数据含有扫描痕迹，造成表面数据平滑度降低。因此，罗切斯特大学研究人员又提出了一种改进的光瞳中继扫描系统[41]，如图6(b)所示，采用两个对称的反射式检流镜的偏转代替xy扫描台，同时采用中继系统使得两块检流镜处于物镜光瞳面，形成远心光路以完成无像差检测。罗切斯特大学研究人员利用SS-OCT检测的自由曲面样品表面矢高达400 μm。目前，SS-OCT技术正处于试验阶段，其检测精度还有待进一步验证。

2.4 干涉测量法

干涉法是检测精度最高的光学元件检测手段，ZYGO公司研制的平面和球面干涉仪已经达到世界公认的检测精度。而非球面光学元件由于其口径内曲率半径各不相同导致检测十分困难。基于非球面检测的精度与通用性的权衡，出现了零位检测与非零位检测，以及子孔径拼接等干涉检测方法[43]。零位检测法主要是设计可以完全补偿非球面法线像差的补偿器，如Offner补偿镜[44]、Dall补偿镜[45]、计算全息补偿器(CGH)[46]等，使得经过被测非球面的光线能够按原路返回，实现和平面或球面类似的“零位”检测。虽然零位检测精度较高，但需要为每一块被测非球面量身定制补偿器，而零位补偿器本身的设计和调整又十分困难。因此，非零位检测法逐渐成为人们关注的焦点，非零位检测不再遵循零位条件，即允许检测光线不沿原路返回，只需要控制探测器接收到的波前像差导致的干涉条纹不超过其分辨极限即可。也就是说一块补偿器可以补偿一系列偏差不大的非球面，大大增加了检测动态范围。然而，正是由于背离了零位条件，非零位检测将为检测结果引入回程误差[47]，需要特定的误差校正算法消除回程误差。另一类干涉检测方法进一步拓宽了非球面检测的动态范围，即子孔径拼接法。该方法将被测面划分为若干子孔径，使得每个子孔径的非球面度大大降低，再利用干涉仪对每个子孔径分别进行检测。有效提高了检测动态范围的同时增加了空间分辨率。对于光学自由曲面的干涉检测目前仍是基于非球面检测思想，下面就几种典型方法的介绍自由曲面干涉检测的发展。

2.4.1 计算全息法

传统光学全息图是在感光材料上记录物光波和参考光波叠加后形成的干涉图样。假如物体并不存在，只知道光波的数学描述，可以利用计算机模拟干涉图样并绘制和复制在透明胶片上，称为计算全息图(Computer-Generated Hologram,CGH)。1971年，CGH开始首次被用于非球面检测[46]。CGH检测非球面的原理如图7所示，球面波或平面波经CGH后不断传播，在被测面处成为与其面形一致的波前，经被测面反射后沿原路返回，形成典型的零位检测法。CGH法检测的技术难点主要集中CGH元件的设计加工与装调。目前采用电子束直写方法加工的CGH，具有很高的空间分辨率，最小线宽能达到10～30 nm[48]；利用激光直写的CGH检测非球面的实验精度已达0.01λrms。CGH的装调目前主要依赖于在主CGH周围设计的辅助装调子CGH图样[49]。

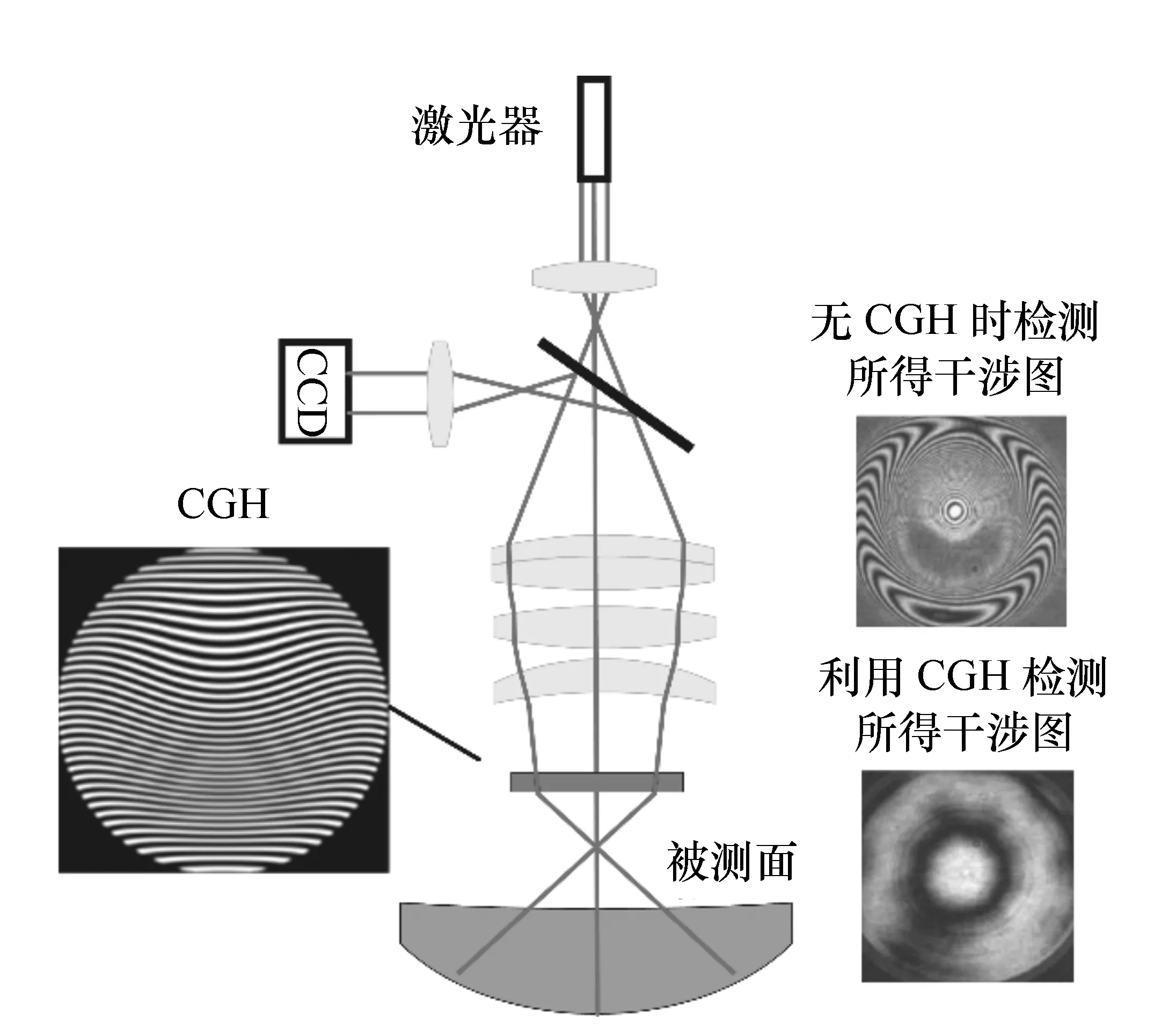
图7 计算全息法检测非球面原理 Fig.7 Principle of aspheric surfaces metrology by CGH

经过多年的发展，CGH技术已经成为非球面检测最为有效的手段之一。国际上，美国的Arizona大学光学中心[50-51]和德国斯图加特大学[52-53]等研究机构在CGH的非球面检验应用中率先展开了深入研究；国内，中科院成都光电所[54-55]、长春光机所[56-57]以及南京理工大学[58-59]等单位也均在该领域取得了重要的成果。

图8 典型CGH示意图 Fig.8 Examples of CGH

由于计算全息法在非球面检测中的成功应用以及高测量精度的优势，众多研究机构都将目光转向了利用CGH进行自由曲面元件面形测量的研究工作。如Arizona大学已成功利用CGH(图8(a))检测了New Solar Telescope(NTS)中的离轴抛物面主镜[51]。日本名古屋大学也成功利用CGH(图8(b))检测望远镜中3.8 m离轴非球面主镜[60]，精度达到80 nm(PV值)。清华大学已经对自由曲面检测的计算全息图制作进行了相关研究[61]。长春光机所针对凸非球面检测所需的CGH设计和制作进行了相关研究[62-63]，并利用计算全息术测量了三次相位板的面形，检测结果(rms 0.068λ)与非零位检测结果一致[64]，同时利用激光直写和离子刻蚀制作得到相位型CGH对口径为846 mm×630 mm的自由曲面进行检测，取得了较好的效果[65]。南京理工大学对CGH法测量自由曲面的不确定度进行了详细分析，并利用相位型CGH检测非旋转对称自由曲面精度达到0.1λ[66]。

但是计算全息术在自由曲面的检测应用中也有其技术瓶颈。零位补偿CGH加工成本高并且由于检测的一对一特性导致测量通用性差，测量动态范围有限，当被检面的面形梯度变化过大时， CGH的刻线会很密，这就加大了加工的难度和误差，使测量精度下降。目前国内外的各个研究机构都是在小梯度变化的光学自由曲面元件上实现了计算全息法检验，但是在实际应用中是大量的梯度变化非常大的自由光学面(如战术头盔中的自由曲面成像镜)，因此CGH在面对大曲率变化自由曲面的检测中受到限制。

2.4.2 部分零位补偿法

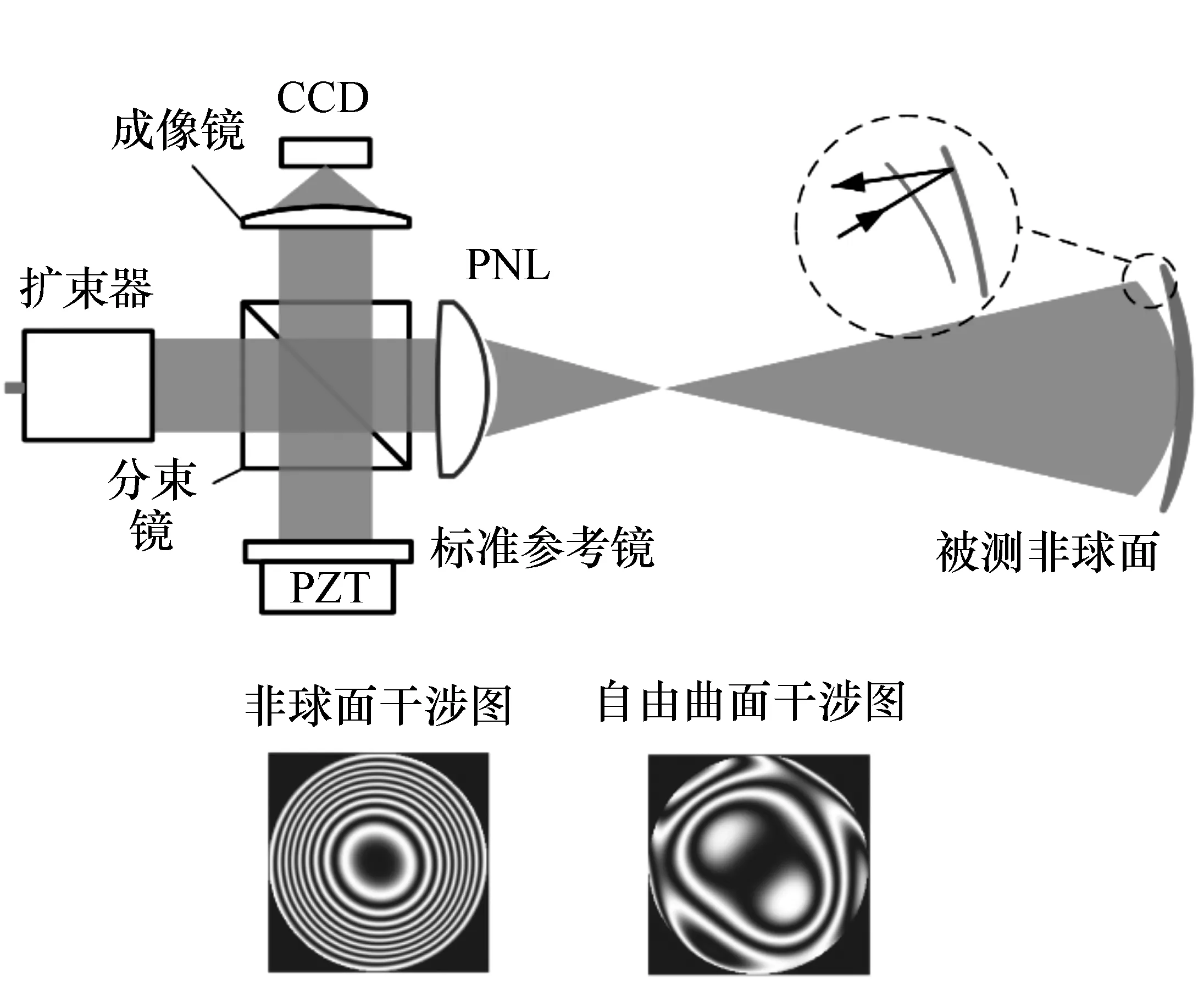
图9 部分零位干涉检测原理 Fig.9 Principle of partial null interferometry

部分零位补偿法起初是针对非球面检测所提出的检测方案[67-69]，如图9所示，在泰曼格林干涉检测结构中利用部分零位镜(Partial null lens,PNL)代替消球差透射球面镜，以补偿非球面的部分法线像差，具有一定的动态范围，所得干涉图如图9左下角所示。但由此将产生一定的回程误差，即入射到被测面的光线不能按原路返回，CCD接收到的被测波前减去被测面理论方程与入射波前方程之差所得到的波前数据和被测面面形误差之间已经失去了传统的“2倍关系”，干涉结构越偏离零位条件，回程误差越大。

浙江大学研究人员曾提出一种基于系统建模的逆向优化重构技术[70-71]可有效地矫正回程误差，该方法通过对干涉机构的精确建模，将实验所得携带回程误差的波前输入模型作为优化目标，将模型中被测面面形误差作为变量(初始值为零，理论面形)，通过该系统模型的迭代光线追迹优化，可以Zernike多项式的形式直接恢复出被测面面形误差。该方法理论上可以对大非球面度、大面形误差非球面实现较准确的面形重构，具有很强的技术通用性。 该部分零位补偿法也可适用于梯度较小的自由曲面检测，所得干涉图如图9右下角所示，利用逆向优化重构技术也可有效地矫正回程误差。然而，值得注意的是，在部分零位法检测大梯度的非球面时，干涉图会出现径向畸变，如图10所示，通过径向映射关系可实现矫正。在检测大梯度的自由曲面时(干涉结构偏离零位程度大)，即使所得干涉图在干涉仪分辨能力范围内，所得到的干涉图由于其波前像差的非旋转对称性将造成干涉图自身非旋转对称形变，该形变将很难进行矫正。由此可见，部分零位法对于自由曲面的检测范围有限，精度还有待进一步验证。

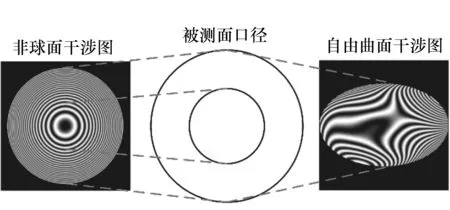
图10 部分零位干涉检测的干涉图畸变 Fig.10 Distortion of interferograms in the partial null interferometry

2.4.3 倾斜波前法

2007年，德国斯图加特大学研究人员提出了倾斜波前补偿非球面的干涉检测思想[72]。其基本原理如图11(a)所示，入射平面波经过微透镜阵列后，引入了与微透镜数目相当的子波前，除轴上子波前以外，其他子波前均以不同的倾角向被测非球面传播，从而补偿非球面不同区域的子区域像差，使得每个子区域的返回的波前像差很小，与参考波发生干涉后的子干涉图可以被探测器分辨，得到可以分辨的干涉图阵列，如图11(b)所示。最后，通过波前恢复算法将被测面面形恢复。

图11 TWI 原理与设备 Fig.11 Principle and device of TWI

国际上以斯图加特大学Wolfgang Osten团队为代表的研究机构对TWI进行了深入研究，该团队2008年利用TWI对900 μm非球面度的非球面检测精度达到0.13λ[73]。2013年，该团队又提出了针对TWI的高精度被测面失调误差优化校正方法[74]，进一步提高了检测精度。2014年，该团队利用TWI对一单点金刚石车削加工的象散自由曲面检测精度达到λ/5PV[75]。国内南京理工大学研究人员[76-77]也对该TWI技术进行了研究，提出了“黑匣子”逆向光路设计法，其对一渐进式眼镜片(顶点曲率半径为142.8 mm，口径为60 mm，最大梯度偏差角为6.273 50°)检测精度达到0.1λPV。

但是从图11(b)中可以明显看出，其干涉图结构复杂，并且每个子波前均明显偏离零位条件，携带巨大的回程误差，为TWI的数据处理带来极大的挑战，在被测面梯度较大时极大地影响检测精度。

2.4.4 子孔径拼接法

上世纪80年代，子孔径拼接干涉检测技术(Subaperture Stitching Interferometry，SSI)逐渐进入人们的视野，1981年，美国Arizona光学中心的C.J.Kin率先提出了子孔径测试概念[78]。通过将被测面或波前分割为不同的子孔径区域分别检测，克服了传统干涉仪的检测限制。SSI将被测面分割为若干个子孔径区域，变换干涉仪检测波前与被测面的相对空间位置，每次仅检测个别子孔径区域，使得被检子孔径区域返回的波前斜率满足奈奎斯特定律，依次恢复各个子孔径面形，进而利用拼接算法重建全口径面形。目前通用的SSI检测技术主要分为圆形子孔径拼接干涉检测(Circular Subaperture Stitching Interferometry，CSSI)[79-86]和环形子孔径拼接干涉检测(Annular Subaperture Stitching Interferometry，ASSI)[87-98]，均是针对非球面光学元件的检测。下面分别介绍这两种技术的应用。

CSSI指的是将利用干涉仪与非球面的相对位置移动(沿轴平移，垂轴平移，绕轴旋转)对不同的圆形子孔径区域进行分别检测进而拼接成全口径面形的检测技术，图12(a)中所示的子孔径布局具有一定的重叠区，是为了后续基于重叠区域最小二乘拟合拼接算法。国外对于CSSI的研究由来已久，商业化设备也日趋成熟，其中以QED公司的SSI系列子孔径拼接干涉仪为代表，图12(b)所示为QED公司的SSI干涉仪设备局部图，可见在CSSI中，一般需要六轴工作台以保证干涉仪对被测面各个子孔径的检测，机构较为复杂，容易产生调整误差。虽然如此，配合误差校准算法，QED公司目前开发的SSI-A已经将可测非球面度拓展至1000λ[79]。

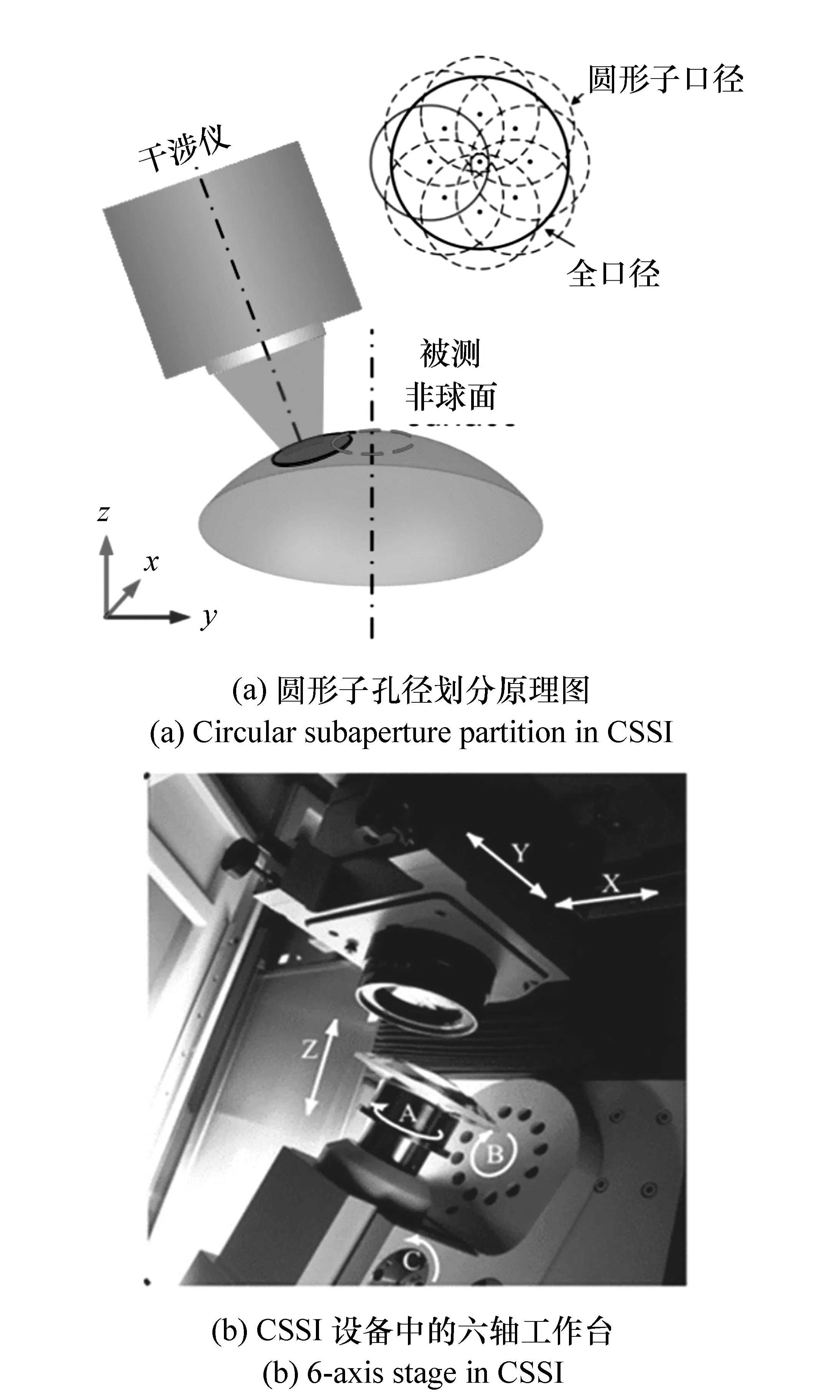
图12 QED公司CSSI设备原理 Fig.12 CSSI device of QED

2010年，ZYGO公司利用两块楔形镜组成可变零位器(Variable Optical Null，VON)[83-84](图13(a)所示)，通过旋转两块楔形镜的角度，为子孔径提供波前倾斜，降低了每个子孔径的条纹密度(图13(b)所示)，提高了横向分辨率，可以检测非球面度达到100λ的深度非球面。

图13 可变零位器及其对子孔径干涉图的影响 Fig.13 VON and the subaperture interferograms

国内的中科院长春光机所[85]、国防科技大学[86-92]等单位均对CSSI技术做出大量的研究工作。但是由于受六轴工作台的机械精度限制，CSSI方法面形拼接精度将受到很大程度的影响，需要辅以非常复杂的误差补偿算法。

相比于CSSI系统的六轴工作台，ASSI仅需要一维移动，大大减小了调整误差来源，同时极大地简化了系统结构。ASSI是采用透射球(Transmission Sphere，TS)产生不同曲率半径的参考球面波，用来匹配被测面不同环形子孔径区域，其原理如图14所示，图14(a)中的被测面可以沿轴向平移，使得不同曲率半径的入射波前与被测面不同环带部分相切，产生可以被干涉仪分辨的环形子孔径干涉图区域(图14(b)所示)。

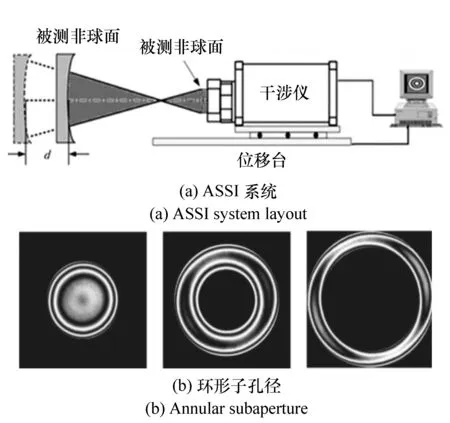
图14 ASSI原理 Fig.14 ASSI principle

ASSI目前被广泛应用于检测旋转对称面(平面、球面及非球面)。以Zygo公司的Verifire[94]型子孔径扫描干涉仪为例，其采用几何扫描拼接方法，目前可测非球面口径达130 mm，非球面度达800 μm，可测面形误差达10 μm。

国内外均对ASSI展开了大量研究，Liu等人[87]最早提出了基于泽尼克圆形多项式的拼接算法。随后，Melozzi等人[88]和Granados-Agustin等人[89]分别提出了基于泽尼克环形多项式的逐次拼接法和全局拼接法，利用重叠区域校正子孔径之间的相对调整误差从而得到全口径数据。国内的子孔径拼接算法研究也取得了很大的进步，中科院成都光电所[90-91]进行了环形Zernike多项式对非球面进行了子孔径拼接研究算法。浙江大学[95-98]采用非球面波前作为参考波前，对每个子孔径进行非零位检测，大大减少了子孔径数目，提高了检测精度的同时扩展了检测动态范围，并采用一种全局逆向优化拼接算法[98]同时完成了子孔径拼接与回程误差去除。

虽然CSSI和ASSI已被成功运用于非球面检测，但对于缺乏旋转对称性的自由曲面的运用依然鲜见报道，目前仅出现对于离轴非球面子孔径拼接的相关报道[99]，值得注意的是，圆形或环形子孔径形状已经不再适用于非旋转对称自由曲面检测，因此对于一般光学自由曲面的SSI技术研究依然没有突破。

3 自由曲面检测难点分析与展望

根据对现行自由曲面检测技术的回顾，并借鉴非球面检测的经验可知，自由曲面的检测依然面临着检测的精度与动态范围之间的矛盾，并且其检测挑战远大于非球面。其主要原因在于:

(1)自由曲面的非旋转对称性质，使得在其在干涉检测机构中不仅面临着旋转对称像差的补偿，而且涉及非对称像差的补偿，而普通的光学元件则难以提供丰富的非对称像差补偿；

(2)虽然区域化的检测方法(哈特曼传感法、TWI、子孔径拼接法)能有效地减小每个检测的子区域像差，但仍然面临着动态范围受被测面梯度所限的难题，并且每个子区域的检测均面临着严重的回程误差影响。

总结上述两大难题即可提炼出对自由曲面检测未来发展的展望：

3.1 非旋转对称像差准零位补偿

自由曲面干涉检测主要面临着非旋转对称像差的补偿。QED公司在非球面检测中曾使用两块楔形板组成的可变零位镜(VON)来补偿边缘的圆形子孔径的非旋转对称像差，如图13所示[83-84]，通过两块楔形平板的之间不同的旋转角度和倾斜角度，可提供不同的低阶像差(如图15所示)，将对于一般自由曲面的低阶非对称像差具有补偿作用，有望实现某些小梯度自由曲面的准零位检测。

国内的国防科技大学也曾做过类似的尝试[100]，使用两块反向旋转的Zernike面板用于补偿离轴的非球面子孔径的彗差和像散，如图16所示。其中每块Zernike板均为CGH，通过相对旋转，可产生不同的彗差和像散用以补偿离轴子孔径像差，扩展非球面子孔径检测的动态范围。

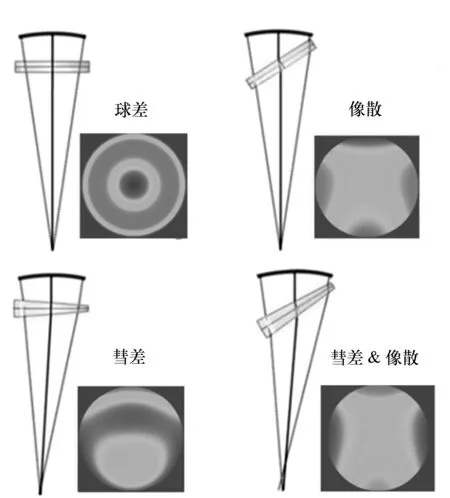
图15 VON可提供的像差补偿 Fig.15 Aberrations compensation of VON

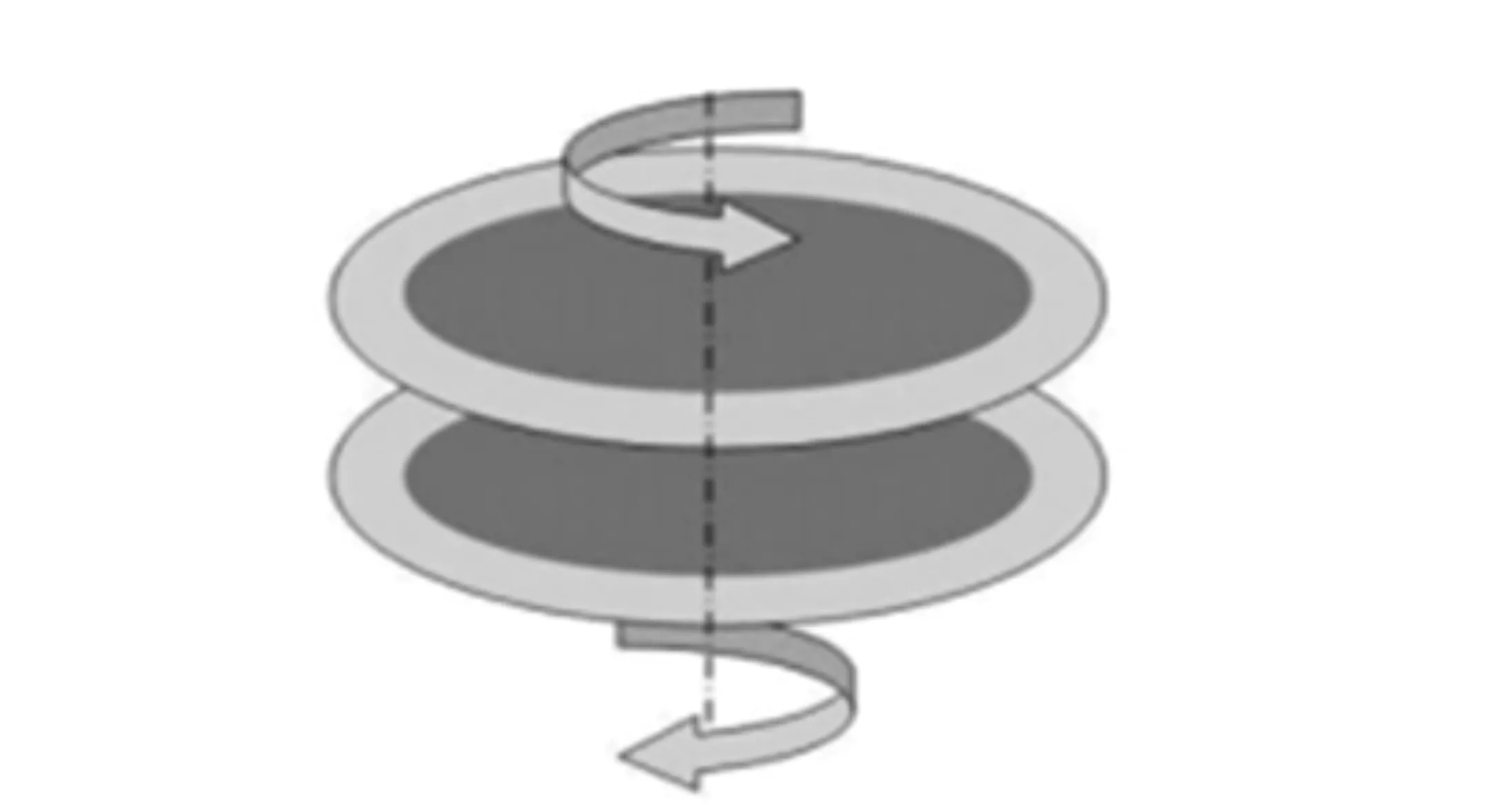
图16 反向旋转的Zernike面板示意图 Fig.16 Schematic diagram of counter-rotating Zernike plates

3.2 子孔径(波前)拼接&回程误差矫正

TWI和子孔径拼接法技术若完成每个子波前(子孔径)的回程误差高精度矫正，将有望在自由曲面通用化高精度检测的道路上更进一步，但是环形子孔径和圆形子孔径的形式明显不再适合自由曲面的子孔径划分。2016年，浙江大学研究人员提出了一种基于非常规子孔径划分的自由曲面子孔径拼接干涉检测(Free form surface subaperture stitching interferometry,FSSI)技术[101-102]。根据被测自由曲面的特征，利用非常规形状的子孔径进行干涉拼接检测，如图17(a)所示，解决了圆形和环形子孔径形状不适用于自由曲面检测的问题；同时，提出一种基于系统模型的多孔径同步逆向优化重构算法用于非常规子孔径拼接,可有效矫正各个子孔径的回程误差。利用该FSSI技术对一口径30 mm的双圆锥面进行了扇形子孔径拼接实验，如图17(b)所示，其检测结果纵向截面轮廓与Taylor Hobson轮廓仪检测结果对比结果一致，检测精度约为1/50λ(rms)。该方法有望在高精度的光学自由曲面检测中得到广泛应用。

图17 非常规子孔径 Fig.17 Irregular subapertures

4 结束语

光学自由曲面因其表面自由度较大，可以针对性地提供或矫正不同的轴上或轴外像差，同时满足现代光学系统高性能，轻量化和微型化的要求，从而逐渐开始成为现代光学工程领域的热点。虽然在设计、加工、检测等方面稳步发展，但成像领域对于光学元件面形的高精度要求却限制了自由曲面的大规模应用。尤其是自由曲面的检测技术已经成为制约其应用的最重要因素。

相比于接触式检测，非接触式检测方法由于可以实现全场无损检测而受到广泛关注。目前大多非接触式自由曲面检测方法的灵感来源于非球面检测，其中夏克-哈特曼传感器法和倾斜波干涉仪虽然可以达到一个很高的测量精度但其动态范围受到微透镜尺寸限制，而且对于大偏离量的自由曲面检测能力不足。结构光三维测量法对工业自由曲面的检测能力较强，而对高精度光学自由曲面的检测精度仍然有待提高。干涉测量法作为目前精度最高的检测手段之一，已经在光学平面、球面乃至非球面的检测领域得到了一致公认。借助于专门设计的补偿器，可以实现高精度的零位干涉检测，但是零位补偿器的设计、检测和装调都会引入误差。而对于那些非规则、非旋转对称的光学自由曲面，则根本无法通过传统的零位补偿器进行补偿，必须使用专门的CGH，而CGH元件加工的高成本，高难度和较难于调整等特性使其测量范围和测量精度均受到限制。以浙江大学为代表的研究机构提出的部分零位法可以提高检测动态范围，但仅限于梯度很小的自由曲面。以罗切斯特大学为代表的研究机构尝试将光学层析法用于自由曲面检测，但其研制的SS-OCT系统较为复杂，对于自由曲面的检测精度还有待进一步验证。基于上述难题，人们将目光转向了子孔径拼接技术，虽然CSSI和ASSI在大口径球面和中度非球面的检测中呈现出高检测精度的特点，但是由于其子孔径特征，使得其在非旋转对称的自由曲面检测中的应用依然没有实质性的突破。而非常规形状的子孔径拼接技术将是一个很好的选择，有望在未来的自由曲面检测中发挥巨大潜力。另外类似于QED公司用于补偿边缘子孔径像差的VON和国防科技大学所使用反向旋转的Zernike面板等离轴像差补偿器也有望成为自由曲面检测的一个重要选择。

[1] TRICARD M. Practical examples of freeform optics[C]. Renewable Energy and the Environment Congress,OSA,2013,FT3B.2:T2B-T3B.

[3] ASLANOV E,DOSKOLOVICH L L,MOISEEV M A. Thin LED collimator with free-form lens array for illumination applications[J].Appl.Optics,2012,51(30):7200-7205.

[4] HUA H. Past and future of wearable augmented reality displays and their applications[J].SPIE,2014,9186:918600-918612.

[5] CURATU C,HONG H,ROLLAND J. Dual-purpose lens for an eye-tracked projection head-mounted display[J].SPIE,2007,6342:63420X-7.

[6] HOWARD J M,WOLBACH S. Improving the performance of three-mirror imaging systems with Freeform Optics[C]. Freeform Optics,OSA,2013,FT2B.6:T2B-T6B.

[7] ROLT S,KIRBY A K,ROBERTSON D J. Metrology of complex astigmatic surfaces for astronomical optics[J].SPIE,2010,7739:139-144.

[8] 张新，许英朝.光学自由曲面的检测方法[J].中国光学,2008,1(1):92-99. ZHANG X,XU Y. Study on free-form optical testing[J].ChineseOptics,2008,1(1):92-99.(in Chinese)

[9] 李圣怡，陈善勇，戴一帆.自由曲面光学器件检测技术[J].纳米技术与精密工程,2005,3(2):126-136. LI SH Y,CHEN SH Y,DAI Y F. Inspection of free-form optics[J].NanotechnologyandPrecisionEngineering,2005,3(2):126-136.(in Chinese)

[10] NEAL D R,ARMSTRONG D J,TURNER W T. Wavefront sensors for control and process monitoring in optics manufacture[J].SPIE,1997,2993:211-220.

[11] PULASKI P D,ROLLER J P,NEAL D R. Measurement of aberrations in microlenses using a Shack-Hartmann wavefront sensor[J].SPIE,2002,4767:44-52.

[12] JEONG T M,MENON M,YOON G. Measurement of wave-front aberration in soft contact lenses by use of a Shack-Hartmann wave-front sensor[J].Appl.Optics,2005,44(21):4523-4527.

[13] GUO W,ZHAO L,TONG C S,etal.. Adaptive centroid-finding algorithm for freeform surface measurements[J].Appl.Optics,2013,52(10):75-83.

[14] 吴青青，张效栋，房丰洲，等.基于波前传感法的立方相位板面形测量[J].光学技术,2014(2):105-112. WU Q,ZHANG X,FANG F,etal.. Shape measurement of the cubic phase plate with wavefront sensing technology[J].OpticalTechnique,2014(2):105-112.(in Chinese)

[15] 赵必玉.高精度面结构光三维测量方法研究[D].成都:电子科技大学,2015. ZHAO B Y. High acuracy surface structured light projection three dimensional measurement[D]. Chengdu: University of Electronic Science and Technology of China,2015.(in Chinese)

[16] NGUYEN H,NGUYEN D,WANG Z,etal.. Real-time, high-accuracy 3D imaging and shape measurement[J].Appl.Optics,2014,54(1):A9-A17.

[17] WANG Z,DU H,BI H. Out-of-plane shape determination in generalized fringe projectionprofilometry[J].Opt.Express,2006,14(25):12122-12133.

[18] DU H,WANG Z. Three-dimensional shape measurement with an arbitrarily arranged fringe projection profilometry system[J].Opt.Lett.,2007,32(16):2438-2440.

[19] HOANG T,PAN B,NGUYEN D,etal.. Generic gamma correction for accuracy enhancement in fringe-projection profilometry[J].Opt.Lett.,2010,35(12):1992-1994.

[20] VO M,WANG Z,HOANG T,etal.. Flexible calibration technique for fringe-projection-based three-dimensional imaging[J].Opt.Lett.,2010,35(19):3192-3194.

[21] WANG Z,NGUYEN D A,BARNES J C. Some practical considerations in fringe projection profilometry[J].Optics&LasersinEngineering,2010,48(2):218-225.

[22] WANG Z,DU H,PARK S,etal.. Three-dimensional shape measurement with a fast and accurate approach[J].Appl.Optics,2009,48(6):1052-1061.

[23] WANG Z,HANB. Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms[J].Opt.Lett.,2004,29(14):1671-1673.

[24] ZHANG S,HUANG P S. Novel method for structured light system calibration[J].Opt.Eng.,2006,45(8):83601.

[25] ZHANG S,HUANG P S. Phase error compensation for a 3-D shape measurement system based on the phase-shifting method[J].SPIE,2005,6000:60000E-12.

[26] HUANG P S,ZHANG C,CHIANG F P. High-speed 3-D shape measurement based on digital fringe projection[J].Opt.Eng.,2003,42(1):163-168.

[27] 徐红兵，任乃飞.基于Atos的光学扫描测量[J].工具技术,2006,40(11):74-77. XU H,REN N. Measuring based on Atos optical scanner[J].ToolEngineering,2006,40(11):74-77.(in Chinese)

[28] 张潇予.基于ATOS扫描的异形件形貌检测与逆向技术研究[D].长春:长春理工大学,2014. ZHANG X Y. Based on the atos profiled morphorpholgy detection and reverse technology research[D]. Changchun:Changchun University of Science and Technology,2014.(in Chinese)

[29] ZUO C,CHEN Q,GU G,etal.. High-speed three-dimensional profilometry for multiple objects with complex shapes[J].Opt.Express,2012,20(17):19493-19510.

[30] ZHONG M,SU X,CHEN W,etal.. Modulation measuring profilometry with auto-synchronous phase shifting and vertical scanning[J].Opt.Express,2014,22(26):31620-31634.

[31] XIAO Y L,XUE J,SU X. Robust self-calibration three-dimensional shape measurement in fringe-projection photogrammetry[J].Opt.Lett.,2013,38(5):694-696.

[32] OLESCH E,HUSLER G,WÖRNLEIN A,etal.. Deflectometric measurement of large mirrors[J].AdvancedOpticalTechnologies,2014,3(3):335-343.

[33] SU T,MALDONADO A,SU P,etal.. Instrument transfer function of slope measuring deflectometry systems[J].Appl.Optics,2015,54(10):2981-2990.

[34] SPECK A,ZELZER B,KANNENGIEβER M,etal.. Inspection of freeform intraocular lens topography by phase measuring deflectometric methods[J].Appl.Optics,2013,52(18):4279-4286.

[35] HUANG L,NG C S,ASUNDI A K. Fast full-field out-of-plane deformation measurement using fringe reflectometry[J].Optics&LasersinEngineering,2012,50(4):529-533.

[36] PAN B,XIE H,WANG Z. Equivalence of digital image correlation criteria for pattern matching[J].Appl.Optics,2010,49(28):5501-5509.

[37] PAN B,XIE H,WANG Z,etal.. Study on subset size selection in digital image correlation for speckle patterns[J].Opt.Express,2008,16(10):7037-7048.

[38] TANG Y,SU X,HU S. Measurement based on fringe reflection for testing aspheric optical axis precisely and flexibly[J].Appl.Optics,2011,50(31):5944-5948.

[40] YAO J,ROLLAND J P. Freeform optics metrology using optical coherence tomography[C]. Optical Fabrication and Testing,2014,DOI:10.1364/OFT2014.OW3B.4:W3B-W4B.

[41] YAO J,XU D,ROLLAND J P. Freeform metrology using swept-source optical coherence tomography with custom pupil-relay precision scanning configuration[J].SPIE,2015,9633:96331A.

[42] DI X,YAO J,ZHAO N,etal.. Scanning customized Swept-source Optical Coherence Tomography(SS-OCT) for the metrology of freeform optical surfaces[C]. Frontiers in Optics,2016,DOI:10.1364/FIO.2016.FW5H.6.

[43] 师途，杨甬英，张磊，等.非球面光学元件的面形检测技术[J].中国光学,2014,7(1):26-46. SHI T,YANG Y,ZHANG L,etal.. Surface testing methods of aspheric optical elements[J].ChineseJ.Optics,2014,7(1):26-46.(in Chinese)

[44] OFFNER A. A null corrector for paraboloidal mirrors[J].Appl.Optics,1963,2(2):153-155.

[45] VEZIN W R. Wavefront errors in the small lens dall null-test-corrigendum[J].J.BritishAstronomicalAssociation,1982:92.

[46] MACGOVERN A J,WYANT J C. Computer generated holograms for testing optical elements[J].Appl.Optics,1971,10(3):619-624.

[47] LIU D,YANG Y,TIAN C,etal.. Practical methods for retrace error correction in nonnull aspheric testing[J].Opt.Express,2009,17(9):7025-7035.

[48] 高峰，朱建华，黄奇忠，等.电子束直写计算全息图[J].中国激光,2001,28(6):556-558. GAO F,ZHU J,HUANG Q,etal.. Computer-generated hologram fabricated by electron-beam direct-writing[J].ChineseJ.Lasers,2001,28(6):556-558.(in Chinese)

[49] 李明.基于CGH的非球面混合补偿检测及离轴光学系统装调的关键技术研究[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2015. LI M. Research on key technology of hybrid null testing of aspheric mirror and off-axis optical system alignment based on CGH[D]. Changchun:Changchun Institute of optics,fine mechanics and Physics,2015.(in Chinese)

[50] ZHOU P,BURGE J H. Fabrication error analysis and experimental demonstration for computer-generated holograms[J].Appl.Optics,2007,46(5):657-663.

[51] ZHAO C,ZEHNDER R,BURGE J H,etal.. Testing an off-axis parabola with a CGH and a spherical mirror as null lens[J].OpticalManufacturing&TestingVI,2005:5869.

[53] REICHELT S,PRUSS C,TIZIANI H J. Absolute interferometric test of aspheres by use of twin computer-generated holograms[J].Appl.Optics,2003,42(22):4468-4479.

[54] FENG J,DENG C,XING T. Design of aspheric surfaces testing system based on computer-generated holograms[J].SPIE,2012,8418:84180R-9.

[55] FENG J,DENG C,XING T. Design and location deviation of the computer generated holograms used for aspheric surface testing[J].SPIE,2013,8788:878820-7.

[56] 赵龙波，张志宇，朱德燕，等.用于非球面检验的激光直写高精度计算全息图制作[J].激光与光电子学进展,2014(11):122-128. ZHAO L B,ZHANG ZH Y,ZHU D Y,etal.. Fabrication of high precision computer generated hologram for aspheric surface testing by laser-direct writing[J].Laser&OptoelectronicsProgress,2014(11):122-128.(in Chinese)

[57] 卢振武，李凤有，刘华，等.利用曲面计算全息图进行凸面非球面检测[J].光电子·激光,2004,15(9):1088-1090. LU ZH W,LI F Y,LIU H,etal.. Testing the convex aspheric surface by using CGH on curved surface[J].J.Optoelectronics·Laser,2004,15(9):1088-1090.(in Chinese)

[58] 席庆奎，朱日宏，陈磊，等.计算全息用于非球面检测的方法[J].激光杂志,2004,25(6):67-69. XI Q K,ZHU R H,CHEN L,etal.. Methods on testing an aspheric with a computer generated hologram[J].LaserJournal,2004,25(6):67-69.(in Chinese)

[59] 王小鹏，高志山，马骏，等.非球面测量中零位计算全息的测量不确定度分析研究[J].光学学报,2011,31(1):111-115. WANG X P,GAO ZH SH,MA J,etal.. Investigation of measurement uncertainty of aspheric surface based on null-computer-generated holography[J].ActaOpticaSinica,2011,31(1):111-115.(in Chinese)

[60] KINO M,KURITA M. Interferometric testing for off-axis aspherical mirrors with computer-generated holograms[J].Appl.Optics,2012,51(19):4291-4297.

[61] 苏萍，谭峭峰，康果果，等.自由曲面零补偿计算全息图离散相位的B样条拟合[J].光学学报,2010(6):1767-1771. SU P,TAN Q F,KANG G G,etal.. B-spline interpolation of scattered phase data of computer generated hologram for null test of freeform surface[J].ActaOpticaSinica,2010(6):1767-1771.(in Chinese)

[62] LIU H,LU Z,LI F,etal.. Using curved hologram to test large-aperture convex surface[J].Opt.Express,2004,12(14):3251-3256.

[63] LIU H,LU Z,LI F,etal.. Design of a novel hologram for full measurement of large and deep convex aspheric surfaces[J].Opt.Express,2007,15(6):3120-3126.

[64] 黎发志，郑立功，闫锋，等.自由曲面的CGH光学检测方法与实验[J].红外与激光工程,2012,41(4):1052-1056. LI F ZH,ZHENG L G,YAN F,etal.. Optical testing method and its experiment on freeform surface with computer-generated hologram[J].InfraredandLaserEngineering,2012,41(4):1052-1056.(in Chinese)

[65] 朱德燕，张学军.高精度相位型计算全息图的设计[J].光学学报,2015,35(7):174-180. ZHU D,ZHANG X. Design of high-precision phase computer-generated-hologram[J].ActaOpticaSinica,2015,35(7):174-180.(in Chinese)

[66] 黄亚，马骏，朱日宏，等.基于计算全息的光学自由曲面测量不确定度分析[J].光学学报,2015(11):156-164. HUANG Y,MA J,ZHU R H,etal.. Investigation of measurement uncertainty of optical freeform surface based on computer-generated hologram[J].ActaOpticaSinica,2015(11):156-164.(in Chinese)

[67] LIU H,ZHU Q,HAO Q. Design of novel part-compensating lens used in aspheric testing[J].SPIE,2003,5253:480-484.

[68] SULLIVAN J J,GREIVENKAMP J E. Design of partial nulls for testing of fast aspheric surfaces[J].SPIE,2007,6671:66710W.

[69] LIU D,YANG Y,LUO Y,etal.. Non-null interferometric aspheric testing with partial null lens and reverse optimization[J].SPIE,2009,7426:74260M-8.

[70] LIU D,SHI T,ZHANG L,etal.. Reverse optimization reconstruction of aspheric figure error in a non-null interferometer[J].Appl.Optics,2014,53(24):5538-5546.

[71] 师途，刘东，张磊，等.非球面非零位检测的逆向优化面形重构[J].光学学报,2014(6):143-150. SHI T,LIU D,ZHANG L,etal.. Reverse optimization reconstruction method for aspheric testing in a nonnull interferometer[J].ActaOpticaSinica,2014(6):143-150.(in Chinese)

[72] GARBUSI E,PRUSS C,LIESENER J,etal.. New technique for flexible and rapid measurement of precision aspheres[J].SPIE,2007,6616:661629-11.

[73] GARBUSI E,PRUSS C,OSTEN W. Interferometer for precise and flexible asphere testing[J].Opt.Lett.,2008,33(24):2973-2975.

[74] BAER G,SCHINDLER J,PRUSS C,etal.. Correction of misalignment introduced aberration in non-null test measurements of free-form surfaces[J].J.EuropeanOpticalSocietyRapidPublications,2013,8(23):6480-6484.

[75] BAER G,SCHINDLER J,PRUSS C,etal.. Fast and flexible non-null testing of aspheres and free-form furfaces with the tilted-wave-interferometer[J].Int.J.Optomechatroni.,2014,8(4):242-250.

[76] 荣四海.点光源阵列多重波面自由曲面检测系统设计与研究[D].南京:南京理工大学,2013. RONG S H. Design and research of the point source multi-wavefront interferometer system[D]. Nanjing:Nanjing University of Science&Technology,2013.(in Chinese)

[77] 沈华.基于多重倾斜波面的光学自由曲面非零位干涉测量关键技术研究[D].南京:南京理工大学,2014. SHEN H.Research on key techniques of tilted wave Interferometer used in the measurement of freeform surfaces[D]. Nanjing:Nanjing University of Science & Technology,2014.(in Chinese)

[78] KIN C J,WYANT J C. Subaperture test of a large flat or a fast aspheric surface[J].J.OpticalSocietyofAmerica,1981,71:1587.

[79] MURPHY P,FLEIG J,FORBES G,etal.. Subaperture stitching interferometry for testing mild aspheres[J].Optics&Photonics,2006:62930J.

[80] CHOW WW,LAWRENCE G N. Method for subaperture testing interferogram reduction[J].Opt.Lett.,1983,8(9): 68-470.

[81] MURPHY P,FORBES G,FLEIG J,etal.. Stitching interferometry:a flexible solution for surface metrology[J].Optics&PhotonicsNews,2003,14(5):38-43.

[82] 程灏波.精密光学元件先进测量与评价[M].北京:科学出版社,2014. CHENG H B.AdvancedMeasurementandEvaluateofPrecisionOpticalElements[M]. Beijing:Science Press,2014.(in Chinese)

[83] TRICARD M,KULAWIEC A,BAUER M,etal.. Subaperture stitching interferometry of high-departure aspheres by incorporating a variable optical null[J].CIRPAnnals-ManufacturingTechnology,2010,59(1):547-550.

[84] MURPHY P,DEVRIES G,FLEIG J,etal.. Measurement of high-departure aspheric surfaces using subaperture stitching with variable null optics[J].SPIE,2009,7426:74260P-10.

[85] 闫力松.子孔径拼接干涉检测光学镜面算法的研究[D].北京:中国科学院大学,2015. YAN L S. Research on the algorithm testing optical mirror by subaperture stitching interferometry[D]. Beijing:University of Chinese Academy of Sciences,2015.(in Chinese)

[86] 陈善勇.非球面子孔径拼接干涉测量的几何方法研究[D].长沙:国防科学技术大学,2006. CHEN SH Y. Geometrical approach to subaperture stitching interferometry for aspheric surfaces[D]. Changsha:National University of Defense Technology,2006.(in Chinese)

[87] LIU Y M,LAWRENCE G N,KOLIOPOULOS C L. Subaperture testing of aspheres with annular zones[J].Appl.Optics,1988,27(21):4504-4513.

[88] MELOZZI A M,PEZZATI L,MAZZONI A. Testing aspheric surfaces using multiple annular interferograms[J].Opt.Eng.,1993,32(32):1073-1079.

[89] GRANADOS-AGUST IAN F I,ESCOBAR-ROMERO J F,CORNEJO-RODR IAGUEZ A. Testing Parabolic Surfaces with Annular Subaperture Interferograms[J].Opt.Rev.,2004,11(2):82-86.

[90] HOU X,WU F,YANG L,etal.. Full-aperture wavefront reconstruction from annular subaperture interferometric data by use of Zernike annular polynomials and a matrix method for testing large aspheric surfaces[J].Appl.Optics,2006,45(15):3442-3455.

[91] HOU X,WU F,YANG L,etal.. Experimental study on measurement of aspheric surface shape with complementary annular subaperture interferometric method[J].Opt.Express,2007,15(20):12890-12899.

[92] CHEN S,LI S,DAI Y,etal.. Experimental study on subaperture testing with iterative stitching algorithm[J].Opt.Express,2008,16(7):4760-4765.

[93] 王孝坤，王丽辉，张学军.子孔径拼接干涉法检测非球面[J].光学 精密工程,2007,15(2):192-198. WANG X K,WANG L H,ZHANG X J. Testing asphere by subaperture stitching interferometric method[J].Opt.PrecisionEng.,2007,15(2):192-198.(in Chinese)

[94] KÜCHEL M F. Interferometric measurement of rotationally symmetric aspheric surfaces[J].SPIE,2009,7389:738916-11.

[95] 张磊，田超，刘东，等.非球面非零位环形子孔径拼接干涉检测技术[J].光学学报,2014,34(8):156-164. ZHANG L,TIAN CH,LIU D,etal.. Non-null annular subaperture stitching interferometry for aspheric test[J].ActaOpticaSinica,2014,34(8):156-164.(in Chinese)

[96] 田超.非球面非零位环形子孔径拼接干涉检测技术与系统研究[D].杭州:浙江大学,2013. TIAN CH. Measurement of Aspheric Surfaces by Non-null Annular Subaperture Stitching Interferometry[D]. Hangzhou:Zhejiang University,2013.(in Chinese)

[97] ZHANG L,TIAN C,LIU D,etal.. Non-null annular subaperture stitching interferometry for steep aspheric measurement[J].Appl.Optics,2014,53(25):5755-5762.

[98] ZHANG L,LIU D,SHI T,etal.. Aspheric subaperture stitching based on system modeling[J].Opt.Express,2015,23(15):19176-19188.

[99] WANG X,ZHENG L,ZHANG B,etal.. Test of an off-axis asphere by subaperture stitching interferometry[J].SPIE,2009,7283:72832J-6.

[100] CHEN S,ZHAO C,DAI Y,etal.. Reconfigurable optical null based on counter-rotating Zernike plates for test of aspheres[J].Opt.Express,2014,22(2):1381-1386.

[101] 张磊.光学自由曲面子孔径拼接干涉检测技术[D].杭州:浙江大学,2016. ZHANG L.Optical free-form surface subaperture stitching interferometry[D]. Hangzhou:Zhejiang University,2016.(in Chinese)

[102] LIU D,ZHOU Y,BAI J,etal.. Aspheric and free-form surfaces test with non-null subaperture stitching interferometry[C]. SPIE/COS Photonics Asia2016,2016:10021N.

Optical free-form surfaces testing technologies

ZHANG Lei1*, LIU Dong2, SHI Tu2, YANG Yong-ying2, LI Jing-song1, YU Ben-li1

(1.KeyLaboratoryofOpto-electronicinformationAcquisitionandManipulationMinistryofEducation,AnhuiUniversity,Hefei230601,China; 2.StateKeyLabofModernOpticalInstrumentation,ZhejiangUniversity,Hangzhou310027,China)

With great degrees of freedom, optical free form surfaces would provide the axial aberrations and off axis ones. Meanwhile, they meet requirements of modern optical systems in high-performance, light weight and micromation, and gradually becomes the hot topic in modern optical engineering. However， their applications have been limited by testing technology of optical free form surface. Most testing methods are still follow those of aspheric surfaces yet. In this paper, we introduce the mathematic description, fabrication and testing of free-form surfaces, especially focusing on several non-contact metrology, such as micro-lenses methods, 3D test with structured light, coherence tomography and interferometry. The technique difficult and development tendency stressing on flexible compensation for rotationally asymmetric aberration and subaperture stitching based on retrace error correction of the regional aberration are introduced as well.

free-form surface testing;interferometry;subaperture stitching;rotationally asymmetric aberration compensation

2017-01-24；

2017-03-01

国家自然科学基金资助项目(No.61675005, No.61440010);安徽省自然科学基金资助项目(No.1508085MF118)；安徽省科技攻关项目(No.1501041136)；国家重点研发专项(No.2016YFC0302202)；安徽大学博士科研启动项目(No.J01003208) Supported by National Natural Science Foundation of China(No.61675005, No.61440010); Anhui Natural Science Foundation(No.1508085MF118); Science and Technology Key Project of Anhui Province(No.1501041136); National Key Research and Development Projects(No.2016YFC0302202); The Doctoral Start-up Foundation of Anhui University(No.J01003208)

2095-1531(2017)03-0283-17

TQ171.65; TN247; TH741

A

10.3788/CO.20171003.0283

张 磊(1987—)，男，安徽舒城人，博士，讲师，主要从事非球面和自由曲面检测、干涉仪研制及应用、光学设计等方面的研究。E-mail:optzl@ahu.edu.cn

*Correspondingauthor,E-mail:optzl@ahu.edu.cn