弹射救生系统延期机构指标极限状态分析评估

李辉，余书山

弹射救生系统延期机构指标极限状态分析评估

李辉1，余书山2

（1.航宇救生装备有限公司应用技术研究部，湖北襄樊441003；2.空军驻航宇公司代表室，湖北襄樊441003）

运用正态分布理论对某型弹射救生装置指令弹射系统中的程序延期机构A和B的延期指标极限状态进行分析，评估出“某型弹射救生装置正、副驾驶员座椅弹射间隔不大于0.67 s”这一事件发生的概率，为由于弹射间隔过小而带来的多座弹射干扰问题的总体决策提供必要理论支持。

正态分布；延期时间；极限状态评估；多座干扰

某型弹射救生装置是由多台火箭弹射座椅和指令弹射系统组成[1-2]。应急弹射时，根据弹射指令座舱内前舱副驾驶员座椅将在程序延期机构A经过0.75 s～0.95 s的延时后弹射出舱，而座舱内前舱左侧正驾驶员座椅最快可在延期机构B经过1.62 s～1.98 s延时后弹射出舱。如取上述数据的极限状态加以简单分析不难看出，“某型弹射救生装置正、副驾驶员座椅弹射间隔最小值为0.67 s（1.62-0.95）”这一事件存在发生的可能，然而如果某型弹射救生装置各座椅之间弹射时间间隔过小则会带来弹射干扰从而影响多座飞机乘员安全救生。因此，本次计算主要对“某型弹射救生装置正、副驾驶员座椅弹射时间间隔不大于0.67 s”这一事件发生概率进行评估，以便设计师系统决策是否需要采取必要措施加以防止。

1 数据及来源

用于本次评估的数据主要由防护救生研发部和火工品部提供。其中包括程序延期机构A用的A1延期管低温试验100发，高温试验100发，延迟时间曲线如图1所示。延期机构B用的B1延期弹高、低温试验各30发，延迟时间曲线如图2所示。

图1 A1延期管延迟时间高、低温试验数据曲线

图2 B1延期管延迟时间高、低温试验数据曲线

2 分析评估

根据试验数据，可分别计算出对应于高、低温条件下的A1延期管延迟时间和延期弹B1延迟时间的样本最大值、样本最小值、样本平均值X¯和样本标准差S，具体计算结果参见表1.其中样本平均值X¯和样本标准差S计算公式[3]如下：

样本平均值：

样本标准差：

表1 A1延期管延迟时间X1、B1延期弹延迟时间X2评估值

由表1中数据简单分析可知，高温条件下，A1延期管延迟时间X1与延期弹B1延迟时间X2之差最小值为0.793 s，而低温条件下，A1延期管延迟时间X1与延期弹B1延迟时间X2之差最小值为0.787 s，均大于0.75 s.

由概率论可知，样本平均值X¯和样本标准差S分别是随机变量的数学期望μ和均方差σ的无偏估计[4]，因此一般都取X¯作为μ的估计量，取S作为σ的估计量。假设A1延期管延迟时间X1服从数学期望为μ1，均方差为σ1的正态分布，即X1～N（μ1，σ12），而延期弹B1的延迟时间X2服从数学期望为μ2，均方差为σ2的正态分布，即X2～N（μ2，σ22）。由概率论可知，延期弹B1与A1延期管延迟时间之差X3=X2-X1应服从数学期望为μ2-μ1，均方差为的正态分布，即X3～N（μ2-μ1，σ12+σ22），其概率密度函数通用形式为：

分布函数通用形式为：

将表1中的A1延期管高、低温延迟时间分别代入公式（3）～（4）中，可计算出高、低温条件下A1延期管各延迟时间对应的概率密度和分布，并绘制成曲线，参见图3、图4.同理将表2中的B1延期弹高、低温延迟时间分别代入公式（3）～（4）中，也可计算出高、低温条件下B1延期弹各延迟时间对应的概率密度和分布。

图3 A1延期管延迟时间X1概率密度曲线

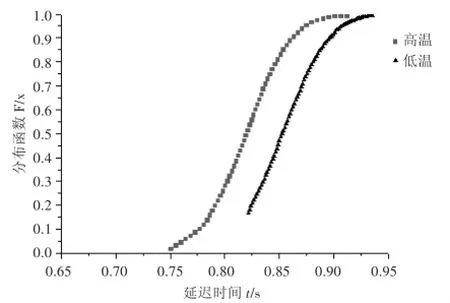
图4 A1延期管延迟时间X1分布曲线

另外，如前所述，由于延期弹B1与延期管A1延迟时间之差X3服从数学期望为μ2-μ1，均方差为的正态分布，即X3～N（μ2-μ1，σ12+σ22），由表3中数据可计算出高温条件下延期弹B1与延期管A1延迟时间之差X3～N（0.918 065，0.001 841 5），低温条件下延期弹B1与延期管A1延迟时间之差X3～N（0.975 097，0.002 427 1）。根据正态分布理论将上述数据代入（4）式中计算得到：

低温条件下，{延期弹B1与延期管A1延迟时间之差X3不大于0.67 s}发生概率为：

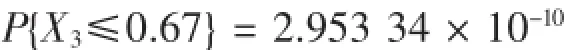
高温条件下，{延期弹B1与延期管A1延迟时间之差X3不大于0.67 s}发生概率为：

同理可计算出：

低温条件下，{延期弹B1与延期管A1延迟时间之差X3不大于0.75 s}发生概率为：

高温条件下，{延期弹B1与延期管A1延迟时间之差X3不大于0.75 s}发生概率为：

则不难得到：

低温条件下，{延期弹B1与延期管A1延迟时间之差X3不小于0.75 s}发生概率为：

高温条件下，{延期弹B1与延期管A1延迟时间之差X3不小于0.75 s}发生概率为：

3 结束语

从已有的试验数据分析可知，高、低温条件下B1延期弹延迟时间X2与A1延期管延迟时间X1之差最小值均大于0.75 s.同时按数理统计中正态分布假设分析可知，无论高、低温条件，“STZ-7型弹射救生装置正、负驾驶员座椅弹射时间间隔不大于0.67 s”这一事件发生概率均非常小，基本可认为此事件不可发生。另外由分析还知高、低温条件下“STZ-7型弹射救生装置正、负驾驶员座椅弹射时间间隔不小于0.75 s”这一事件发生概率均非常大。

[1]徐立珍，周曼娜，刘奔，等.航空安全与装备维修技术学术研讨会沦文集[C].航空搜救营救装备发展建设研究，2014：365-368.

[2]徐辉，王新华.飞行员“生命保护神”一航空救生装备简介[J].环球军事，2008，177（7）：58-59.

[3]GB4882.数理统计处理和解释正态性检验[S].北京：中国标准出版社，2001.

[4]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，1990：56-78.

The Analysis Evaluation of the Ejection Escape System Delay Device Index LimitState

LI Hui1，YU Shu-shan2
（1.AVIC Aerospace Life-support Industries.Ltd.，Xiangfan Hubei 441003，China；2.The Air Force Representatives Office of AVIC Aerospace Life-support Industries.Ltd.，Xiangfan Hubei 441003，China）

By analyzing the delay index of the limit state of program extension mechanism of a type of ejection device command ejection system A and B normal distribution theory，the probability assessment of a certain type of ejection device and deputy driver’s seat ejection interval not more than 0.67 s of this event，to provide the necessary theoretical support for the overall decision a rebound jamming problem caused by the ejection interval is too small.

normal distribution；delay time；limit state evaluation；multiseater interference

V244.21

A

1672-545X（2017）01-0043-03

2016-10-27

李辉（1973-），男，湖北襄阳人，硕士，高级工程师，从事于飞机弹射座椅的性能设计和可靠性设计工作。