爆破掘进巷道支护锚杆的振动响应研究
胡帅伟
摘要:为了研究爆破掘进施工对巷道支护锚杆的影响,本文采用结构动力学理论,从理论上推导出了锚杆在动荷载作用下的运动规律,计算出锚杆上的轴力与剪切力变化;分析研究了端锚式锚杆在爆破动荷载作用下的动力响应特征。结果表明:不同锚杆长度时锚杆受力状态不同,锚杆会产生的轴向变形和弯曲变形,对于同一长度的锚杆,弯曲变形要大于轴向变形,因此锚杆是以弯曲变形为主导形式。靠近巷道的锚杆段可能受压也可能受拉,但锚杆较长时锚杆整体受拉,且无论轴力还是剪力都比较小,也就是说爆破振动扰动一般不会使锚杆产生破坏失效。成果对掘进爆破安全技术的提高具有一定的指导意义。
Abstract: In order to study the influence of underground blasting seismic waves on the bolt supporting structure, in this paper, the dynamic response characteristics of the end anchored bolt under blasting load are studied by using the structural dynamics theory. Bolt stress state is different when the bolt length is different. The vibration will induce axial deformation and bending deformation in the bolt. For same bolt length, the bending deformation was bigger than axial deformation. Thus, the bending deformation was the leading deformation in the bolt. The bolt segment near the tunnel may be under pressure or tension, but the whole bolt is under tension when the bolt is longer. Whether axial force or shear in bolt is relatively small, which means that blasting vibration generally does not cause bolt damage and failure. The results have some significance to improve safety blasting technology.
關键词:地下爆破;爆破地震波;锚杆
Key words:underground blasting;blasting seismic wave;bolt
中图分类号:TD824 文献标识码:A 文章编号:1006-4311(2017)18-0117-04
0 引言
锚杆支护是在边坡、岩土深基坑等地表工程及隧道、采场等地下硐室施工中采用的一种加固支护方式。巷道中锚杆支护结构在实际工程中除了受地压等静载外,还常受到爆破、采掘、地震等动载作用,而爆破振动被认为是钻孔爆破特别是地下工程爆破中各种公害之首,对结构产生的影响甚至是灾难性的,造成无法挽回的损失。迄今为止,对于锚杆支护的研究主要集中在静载作用下的现场拉拔试验、模型试验和数值分析,而对于动载作用下锚杆力学性能的研究比较少见,基本上也只是停留在试验阶段。Gisle和Arne[1]根据现场试验研究得出充分注浆锚杆可以应用在作业面上或接近作业面处的结论。Ana Ivanovi[2-4]针对锚固系统建立了集中参数模型,探讨了外部激发荷载对锚固系统的动力特性的影响;同时她还探讨了系统固有频率及其参数影响。刘国华[5]、石洪超[6]和孙金山[7]等分别采用了不同数值模拟工具探讨了爆破开挖荷载下围岩的振动响应和稳定性问题。单仁亮[8],周纪军[9],张哲诚[10]等通过模型试验对锚杆在动力荷载下进行了专门的研究。总结发现,爆破振动对锚杆支护结构作用机理研究相对较少,大多停留在定性分析和数值模拟与试验层面上。本文侧重在理论上推导出锚杆在动荷载作用下的运动规律,通过它的运动规律计算出锚杆上的轴力与剪切力变化。研究成果对钻孔爆破法施工中锚杆支护结构有重大的指导作用,判断在爆破的过程中,锚杆是否发生破坏具有重要参考意义。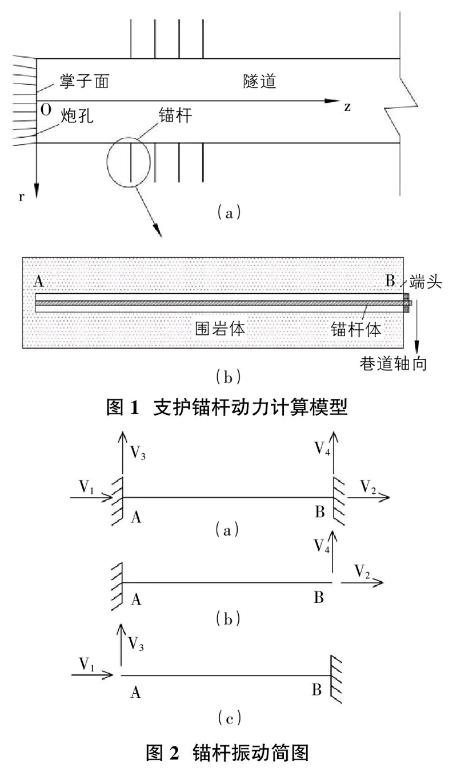
1 巷道围岩中锚杆振动的计算模型
如图1所示,在爆破施工过程中,前方掌子面爆破施工产生爆破振动,将引起后方既有支护锚杆产生振动,锚杆的振动是来自于锚杆四周的围岩振动引起的,因此锚杆端部A、B的振动则完全由自身端部的围岩振动决定的,而锚杆中部的振动则是由两端的振动共同作用引起。锚杆振动计算简图如图2(a)所示。由于锚杆四周的围岩及端部的锚固对锚杆有约束作用,将锚杆A、B端的运动考虑为固定和自由状态下的叠加,即将锚杆支护结构的振动分解成如图2(b)、(c)所示的两个结构振动的叠加。
2 巷道围岩中锚杆振动规律解析解
2.1 锚杆的轴向振动
将图2(a)中锚杆的横向振动与轴向振动分开讨论。锚杆的轴向振动计算简图如图3所示。
G为剪切模量,钢材取0.792×105MPa。
3 计算实例与结果讨论
某巷道掘进开挖工程采用微差爆破技术施工,循环进尺为1.5m,孔径40mm,周边孔间距45cm。巷道为圆形,半径为2.5m。采用乳化炸药,密度1100kg/m3,爆速3200m/s,炸藥单耗0.75kg/m3。岩体为风化的花岗岩,密度2350kg/m3,弹性模量18GPa,泊松比0.25。设荷载衰减指数4000。锚杆采用直径为20mm的HRB400钢筋。
文献[12]给出的是巷道围岩在爆炸瞬间有了最大初位移以后的运动规律,因此上述锚杆也是对应于围岩有了最大初位移以后的运动规律和受力状态。在前述爆破振动计算实例中,若锚杆直径为20mm,长度分别取1.0m、1.5m、2.0m,将相关参数代入式(3),(4),(9)中,则爆破荷载引起的锚杆位移如图6-13所示。
3.1 锚杆轴向位移在锚杆不同位置上的变化
3.2 锚杆轴力在锚杆不同位置上的变化
3.3 锚杆剪力在锚杆不同位置上的变化
从图5-7可以看出,在巷道轴向距离相同,靠近巷道围岩表面的锚杆部分始终是沿着径向向内运动,而另一端可能是沿着径向向外运动也可能向内运动,这与锚杆的长度有关。锚杆中部的运动主要是沿着径向向内运动,这与靠近巷道围岩表面的锚杆部分的振动振幅要大于另一端振动的振幅叠加所导致的。从图5可以看出,对于不同长度的锚杆,当锚杆轴向位移过大时,锚杆会被围岩挤出,从而使锚杆失效。
从图8-10可以看出,在巷道轴向距离相同,不考虑锚杆之前的受力状态,靠近巷道围岩表面的锚杆部分可能受拉也可能受压,远离围岩表面的部分始终受拉,这与不同锚杆的长度对应于远离围岩表面的锚固段的速度方向不同,导致锚杆的振动产生的应变状态不同导致,锚杆总体处于受拉状态。
从图11-13可以看出,在巷道轴向距离相同,锚杆的剪切力的大小与径向距离有关,对于同一长度的锚杆,轴向距离越大,剪切力越大,这是由于,轴向距离越大,它的竖向位移也越大,导致它的剪切变形越大,所以剪力会越大,而巷道表面的锚杆由于没有位移,则剪切变形为零,因此它的剪切力为零。对于不同长度的锚杆,端部竖向位移不同,导致锚杆的剪力不同。
相对于锚杆材料强度(?覫20mm的HRB400钢筋锚杆承载能力设计值为113kN)来讲,无论轴力还是剪力都比较小,也就是说爆破振动扰动一般不会使锚杆产生破坏失效。
4 结论
本文通过理论推导,运用锚杆的振动微分方程,求解出锚杆的振动方程随轴向距离、径向距离和时间的变化规律,然后通过锚杆的振动方程求出求解出锚杆的应变得出锚杆的受力状况,主要结果如下:
①总结发现,锚杆会产生的轴向变形和弯曲变形,对于同一长度的锚杆,弯曲变形要大于轴向变形,因此锚杆是以弯曲变形为主导形式,此结论与单仁亮[8]的实验结论相一致。②当锚杆达到一定的长度时,由于振动叠加以后锚杆位移过大,导致锚杆会被围岩挤出,使锚杆失效。③不同锚杆长度时锚杆受力状态是不同的,靠近巷道的锚杆段可能受压也可能受拉,但锚杆较长时则锚杆整体受拉。相对于锚杆材料强度,无论轴力还是剪力都比较小,也就是说爆破振动扰动一般不会使锚杆产生破坏失效。
参考文献:
[1]S.GISLE, M.ARNE. The influence of blasting on grouted rock bolts[J].Tunneling and Underground Space Technology,1995,13(1):65-70.
[2]Ivanovi A, Neilson R D, Rodger A A. Lumped parameter modelling of single-tendon ground anchorage systems[J].Geotechnical Engineering,2001,149(2):103-113.
[3]Ivanovi A, Starkey A,Neilson R D, et al. The influence of load on the frequency response of rock bolt anchorage[J].Advances in Engineering Software, 2003, 34(1112):697-705.
[4]Ivanovi A, Neilson R D. Influence of geometry and material properties on the axial vibration of a rock bolt[J].International Journal of Rock Mechanics and Mining Sciences, 2008, 45(6): 941-951.
[5]刘国华,王振宇.爆破荷载作用下隧道的动态响应与抗爆分析[J].浙江大学学报(工学版),2004,38(2):204-209.
[6]石洪超,丁宁,张继春.爆破动力作用下小净距隧道围岩振动效应分析[J].爆破,2008,25(1):74-78.
[7]孙金山,金李,姜清辉,等.地下洞室爆破开挖过程中地应力瞬态调整诱发节理围岩松动机制研究[J].振动与冲击,2011,30(12):28-34.
[8]单仁亮,周纪军,等.粘结式锚杆在爆炸动载下轴向应力分布研究[J].岩土力学,2011,32(10):2965-2971.
[9]周纪军,单仁亮,贾志欣,耿慧辉,赵宇飞,刘立鹏.近区锚喷结构的爆破振动特性研究[J].岩土力学,2013(08):2225-2230.
[10]张哲诚,张向东,刘源浩,等.横向简谐荷载作用下端锚黏结式锚杆黏结性试验研究[J].煤炭学报,2016,41(6):1407-1415.
[11]李东旭.高等结构动力学[M].北京:科学出版社,2010.
[12]张涛,陈士海,张伟,逄焕东.掘进爆破振动作用下支护结构的安全距离[J].爆破,2014(01):133-137.

