模糊逻辑中的一些问题与研究进展

裴道武

(浙江理工大学 理学院, 浙江 杭州 310018)

模糊逻辑中的一些问题与研究进展

裴道武

(浙江理工大学 理学院, 浙江 杭州 310018)

在过去的30多年里,模糊逻辑在理论和应用2个方面都取得了较大的进展.时至今日,在该领域中还存在一些值得关注的研究方向和研究课题.就以下4个问题对于这个领域的部分进展展开讨论:为什么需要模糊逻辑?早期模糊逻辑有哪些不足?现代模糊逻辑有哪些主要成就?以及模糊逻辑未来何处去？

模糊逻辑; 三角模; 剩余蕴涵; 计量逻辑; 模糊推理

近年来,随着人工智能技术的再次兴起,作为人工智能核心理论基础之一的模糊逻辑,也受到学术界的关注.

第1个问题 为什么需要模糊逻辑?

在回答这个问题之前,先简要回顾逻辑学的发展历程[1-4].

逻辑学,又称为形式逻辑学,创立于古希腊时代,主要代表人物是亚里士多德(A. Aristoteles,384 B.C.—322 B.C.).形式逻辑学是研究人类思维与推理的学问;又称为经典逻辑,或传统逻辑.形式逻辑学包含三大定律:同一律、矛盾律和排中律.

到19世纪中叶,随着数学的发展,数理逻辑学应运而生.数理逻辑学是用数学方法研究逻辑学的学问;也叫符号逻辑,或二值逻辑.其代表人物有英国逻辑学家布尔(G. Boole,1815—1864)和德国逻辑学家弗雷德(G. Frege,1848—1925).布尔的代表性著作为《逻辑的数学分析》(1847)和《思维规律的研究》(1854),而弗雷德的代表性著作为《概念演算》(1897).在弗雷德的工作中,命题演算的形式演绎系统已经成型.

经过众多逻辑学家的工作,经典逻辑的形式演绎系统L逐步完善.在这个命题演算系统中,命题已经被形式化地用符号来表示,公式集合F(S)可以由原子公式集合S={p1,p2,…}通过命题联结词┐(非)、∧(合取)、∨(析取)、→(蕴涵)和↔(等价)等生成.命题的真值域为二元集合{0,1},其中,0表示假,1表示真.

语义理论的基本概念亦已形成,包括赋值、重言式、矛盾式和可满足式等.

语构理论的框架亦已建立,公理系统L包括3条公理和1条推理规则(假言推理规则,即modus ponens,简记为MP).相应地,定理与证明、理论与结论等概念也已经系统化.特别地,这个系统的可靠性与完备性也已经获得证明.

几千年来,经典逻辑已经成为人类最重要的思想财富,构成了自然科学、人文社会科学的几乎所有学科共同的逻辑基础.

尽管经典逻辑在人类科学技术发展史中发挥了十分重要的作用,它还是有其局限性的.比如,人类在处理不确定性问题和现象时,常常受到排中律的约束,科学研究、工程领域与包含人类的系统中遇到的许多问题的答案都不是非此即彼、黑白分明的.

在逻辑学历史上,对于传统逻辑中排中律的质疑导致了2次重大的突破.

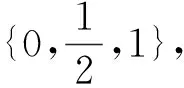
第二次突破发生在20世纪60年代,其代表性成果是模糊集与模糊逻辑理论的建立.这个工作主要归功于美国控制论专家扎德(L. A. Zadeh)[5]于1965年发表的开创性论文.

所谓模糊集(Fuzzy set),通俗地说,就是边界不分明的集合;精确地说,就是从论域到[0,1]的映射,即隶属函数.扎德在数学中首次引入程度化思想方法,将传统逻辑中命题的真值集合扩展到实数的单位区间[0,1].

模糊逻辑的另一个代表人物是美国逻辑学家马里诺斯(P. N. Marinos)[6],他于1969年首次建立了模糊逻辑的基本体系,并且将之应用于开关系统.

综上所述,模糊逻辑的建立是人类认识水平不断提高的必然产物,是人类处理模糊现象的必不可少的逻辑基础;此后模糊逻辑的发展历程也证实了这一点.

1 早期模糊逻辑的不足

早期模糊逻辑的主要研究领域包括:模糊逻辑命题联结词的研究(否定、析取、合取、蕴涵等),模糊逻辑电路的研究(模糊逻辑器件、逻辑函数的表示与极小化等),以及模糊逻辑系统的研究(代数结构、语义性质、量化命题研究等)[7-8].

在早期模糊逻辑的应用研究中,许多工作集中于模糊推理的模型与算法研究,以及模糊控制系统的建立和运用.

这里值得提到的是扎德于1973年提出了模糊推理的合成推理方法(compositional rules of inference),文献中简称为CRI方法[9-11].

此后,英国控制论专家将CRI方法运用于控制领域,建立了模糊控制的理论和方法,并且将这个方法成功地应用于具体的控制流程;在学术界和工程领域产生了比较深远的影响[12-13].

在模糊逻辑领域的第一个深刻的理论成果是由捷克逻辑学家帕维卡(J. Pavelka)[14]于1979年完成的.在他的3篇著名论文中,基于剩余格理论,建立了对应于卢卡西维茨蕴涵的2个形式系统(有限值和连续值情形),并且分别证明了它们的语义完备性.

第2个问题 早期模糊逻辑有哪些不足?

要回答这个问题,不得不提到发生于1993年的一场关于模糊逻辑作用的大论战.

1993年7月,在美国第11届人工智能年会上,美国加州大学伯克利分校的爱坎(C. Elkan)[16]宣读了题为“模糊逻辑似是而非的成功”的报告,随即引起人工智能和模糊界的争议,从而爆发了一场论战.

此后,世界著名期刊《IEEE Expert》组织了专题讨论,并且于1994年出版专集刊登了爱坎的大会报告与18位相关领域的知名专家的评论,同时刊登了爱坎对这些评论的答复.1995年,吴望名[17]在《模糊系统与数学》上刊文专题介绍了这场争论.

尽管参与争论的各位专家各持己见,似乎没有得到能为各方接受的共识;但是,这场争论对于模糊逻辑的发展却起到了相当重要的推动作用.

笔者认为,这场学术论战至少具有以下2个历史作用:

首先,通过这场争论,在主流人工智能界与模糊界之间实现了沟通,公开了学术界对模糊逻辑的一些片面认识,同时也暴露了模糊逻辑自身的缺陷与不足.

比如,在模糊逻辑的文献中,“模糊逻辑”一词存在2种不同的含义:一种用于表示经典逻辑的逻辑推广,如模糊开关逻辑、逻辑联结词、形式演绎系统等;另一种则是模糊集合理论与方法的别称.这种歧义也是引起争论的重要原因之一.

通过这场争论,扎德[18]提出了狭义模糊逻辑(fuzzy logic in narrow sense)与广义模糊逻辑(fuzzy logic in wide sense)的名称,分别对应于以上2种情形.

其次,这场争论吸引了学术界对模糊逻辑的关注,有力地促进了模糊逻辑的发展,直接导致了现代模糊逻辑的诞生.

在这场争论中,人们看到了模糊逻辑的一些不足之处.比如,模糊推理中缺少误差的度量,导致复合推理链中误差的积累影响到推理结果的精确度;这种重应用轻基础的现象很普遍.又比如,模糊推理方法不符合逻辑要求,规则合成具有很强的随意性;这种重推理轻逻辑的问题也是十分严重的,直接导致推理结果的可信度不高.另外,缺少模糊逻辑的形式化与实用化研究,这是重语义轻语构的倾向.

2 现代模糊逻辑研究的主要成就

笔者于2004年在文献[19]中曾经对模糊逻辑十年(1993—2003)的若干进展做过一次综述,主要围绕模糊逻辑的形式化、谓词逻辑系统,以及模糊推理的逻辑基础等3个问题展开论述.本文也可以看成是文献[19]的续篇.

第3个问题 现代模糊逻辑有哪些主要成就?

这个问题有点大,只能就笔者的理解,大致介绍在模糊逻辑近30年的发展历程中6个方面的成就,包括:模糊逻辑的形式化研究、模糊逻辑与模糊推理的结合研究、广义重言式理论、计量逻辑学、模糊蕴涵的研究,以及模糊数学的逻辑基础.

第1个成就 模糊逻辑的形式化研究.

在众多的模糊逻辑系统中,比较著名的模糊逻辑形式系统有形式系统L*、形式系统BL(Basic Logic)、形式系统MTL(Monoidal T-norm based Logic),以及形式系统Π.

王国俊[21-22]提出的形式系统L*由3个部分构成:公式集F(S):是由原子公式集S,通过命题联结词集合{┐,∨,→}生成的自由代数;公理集Axm(L*)中包含了14条公理(后来简化为10条);推理规则集包含2条规则,即MP规则和交规则(后来简化为一条,即MP规则).

回顾系统L*的研究历程,1996—1997年,提出了语构和语义的基本形式[21-22];1998—2000年,主要是语构方面的研究[23-24];2000年提出了R0代数的理论[2];2002年,系统L*的完备性获得证明[25-29].

由于历史的缘故,基于三角模的模糊逻辑总是受到很多的关注[30-31].在这种模糊逻辑中,合取联结词由某个适当选择的三角模T给出解释;蕴涵联结词由T诱导的剩余蕴涵R(定义为R(a,b)=sup{c∈[0,1]-T(a,c)≤b},a,b∈[0,1])给出解释;否定联结词由R的自然否定n(定义为n(a)=R(a,0),a∈[0,1])给出解释;析取联结词则由T关于n对偶的三角余模S(定义为S(a,b)=n(T(n(a),n(b))),a,b∈[0,1])给出解释.

因此,基于三角模的模糊逻辑可以由一个三角模完全给出解释.

基于三角模的模糊逻辑系统具备许多优良的逻辑性质,这些性质基本反映了人类思维和常识推理的逻辑特征.因此,这种模糊逻辑系统已经被广泛地应用于模糊推理和其它人工智能领域中.

在相关文献中,基于三角模的模糊逻辑理论主要有2个:一个是基于连续三角模的模糊逻辑理论,另一个是基于左连续三角模的模糊逻辑理论[30].

基于连续三角模的模糊逻辑理论的创始人是捷克科学院院士哈耶克(Hjek:Basic Logic,BL)[20].

与系统BL对应的代数结构为BL代数,即满足准线性和连续性的剩余格.

关于系统BL的完备性及对应的谓词逻辑系统,已经有比较系统的研究成果.特别地,以下的标准完备性结论是十分重要的.

定理 2.1[32]系统BL是所有基于连续三角模的模糊逻辑的共同形式化.

基于左连续三角模的模糊逻辑理论由西班牙的爱斯太瓦(F. Esteva)和高德(L. Godo)于2001年共同创立的,他们称之为基于三角模的Monoidal逻辑(Monoidal T-norm based Logic),简记为MTL[33].

基于左连续三角模的模糊逻辑是基本逻辑BL的发展,其公式集合与BL相同,推理规则也只有1条,即MP规则.

系统MTL与BL的主要区别在于,MTL将合取联结词∧作为独立的联结词,而且二者的公理略有相同,系统MTL的公理模式有10条.

系统MTL具有以下几个重要的模式扩张:弱幂零极小逻辑(Weak Nilpotent Minimum),简记为WNM;对合MTL逻辑(Involutive MTL),简记为IMTL;以及幂零极小逻辑(Nilpotent Minimum),简记为NM.

系统MTL的语义代数模型为MTL代数,即满足准线性的剩余格.

关于系统MTL及其模式扩张的完备性及相应的谓词逻辑系统研究,已经取得许多有意义的成果.特别地,以下标准完备性结论也是重要的.

定理 2.2[34]系统MTL是所有基于左连续三角模的模糊逻辑的形式化.

于2003年得到以下有趣的结果:

定理 2.3[35]1) 系统L*和NM是等价的,并且R0-代数和NM代数是同样的代数系统.

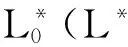
根据这个结论,系统L*实际上是MTL的模式扩张.因此,这个系统也是基于三角模的模糊逻辑.事实上,这个逻辑就是基于幂零极小三角模的模糊逻辑,而R0蕴涵就是由幂零极小三角模诱导的剩余蕴涵[4].

在模糊逻辑理论中,考虑代数类之交的形式化问题也是有意义的工作.捷克逻辑学家辛特拉(P. Cintula)[36]于2001年考虑了几个代数簇的交集的公理化:1)Π:MV代数类和Π-代数类的交;2)G:MV代数类和Gödel代数类的交;3) GΠ:Gödel代数类和Π-代数类的交;4)GΠ:以上3个代数类的交.这里,值得特别关注的是形式系统Π.

形式系统Π的构成:公式集F0(S)是由S生成的

型自由代数;推理规则有2条:MP规则和△-添加规则;公理模式有14条.

比较有影响的模糊逻辑形式化的其他工作还有:直觉主义逻辑IL(IntuionisticLogic)、乘加直觉主义线性逻辑MAILL(MultiplicativeAdditiveIntuionisticLinearLogic)、Monoidal逻辑ML(MonoidalLogic)、一致模逻辑UL(UninormLogic),以及格蕴涵代数的逻辑研究等[37-38].

第2个成就 模糊逻辑与模糊推理的结合研究.

已知模糊推理最基本的模型是模糊取式FMP(fuzzymodusponens):给出一个模糊规则“如果A,那么B”,翻译为蕴涵式A→B,以及一个模糊输入A*,寻求模糊输出B*,其中A和A*是论域X上的模糊集,B和B*是论域Y上的模糊集.

以上推理模型可以形式化地表示为:

FMPA→B,A*⟹B*.

扎德[9-10]于1973年提出了CRI方法:首先使用适当的模糊蕴涵R,将A→B转化为X×Y上的模糊关系R,它在点(x,y)处的隶属度为

R(x,y)=R(A(x),B(y));

其次将小前提A*和模糊关系R做合成得到结果

B*:B*=A*∘R,

王国俊[39,2]基于对模糊推理方法的分析,指出:在使用CRI方法求解FMP问题时,合成运算sup-∧不是十分合理的,背离了推理的语义蕴涵的原则.因此,他于1999年提出了模糊推理的新方法,叫做全蕴涵三I方法,简称为三I方法,作为对传统的CRI方法的改进.

王国俊[2]又于2000年借助于部分赋值方法,将三I方法纳入模糊逻辑的框架之中.

关于三I方法的文献比较多,王国俊等[40]曾撰文对此进行综述.这些研究主要集中于以下课题的工作:具体算法的研究、一般算法及其还原性的研究[41-43]、连续性的研究[44]、一阶系统的研究[45]、逻辑基础的研究[46-47]、三I方法的变异方法研究(反向算法、约束度算法、支持度算法、模糊熵算法)[48]、三I方法的应用研究(模糊控制器响应能力分析)[49-54]等.

另外,也有文献讨论更一般模糊推理模型的三I算法、区间值三I算法,以及模糊推理的非模糊形式[55].

第3个成就 广义重言式理论的建立.

这方面的工作开始于1998年,这类文献主要集中于讨论不同多值逻辑与模糊逻辑系统中的广义重言式理论、带参数模糊逻辑系统中的广义重言式理论,以及广义重言式理论的应用(语构研究、推理研究)[56].

第4个成就 计量逻辑学的建立.

王国俊开创性地将数值计算的方法引入抽象的形式逻辑中,基于公式的平均真度概念,于1998年建立了积分语义学理论[2,57-58],并进而于2001年建立了计量逻辑学的理论体系[59-60].

在这方面的文献中,大部分工作集中于公式的真度理论、公式间的积分相似度、公式间的伪距离、公式集中的近似推理,以及理论的相容度和发散度等[61-64];有关论述参见文献[65-66].

第5个成就 模糊蕴涵的研究.

在逻辑系统的研究中,蕴涵起着非常重要的作用,而模糊蕴涵的研究已经成为模糊逻辑研究的重要方向.关于这方面的成就,建议参考文献[67-68],这里不展开讨论.

第6个成就 模糊数学的逻辑基础研究.

在相关文献中,已经被形式化的项目有:属于关系(∈)、隶属函数、模糊集的运算、扩展原理、模糊关系、模糊关系的运算、模糊关系类的结构、模糊预序关系、模糊相似关系、模糊分划等.

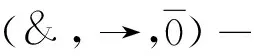
模糊数学的若干项目在FCT中形式化后,论域中的元素x、模糊集、n元模糊关系、三角模*、剩余蕴涵R、取小运算、取大运算分别形式化为对象变量x、一元谓词符号、n元谓词符号、强合取&、蕴涵联结词→、弱合取∧、弱析取∨.

值得指出的是,关于模糊逻辑的代数研究工作,也取得了相当卓越的成就,这方面的工作参见文献[70-71].

3 模糊逻辑研究的未来

第4个问题 模糊逻辑未来何处去?

模糊逻辑未来的主要研究方向有:模糊逻辑形式系统的研究、模糊推理合理性的研究、基于程度化的模糊推理方法的研究、模糊量词的研究,以及模糊推理的应用研究等.

关于模糊逻辑形式系统的研究,尽管有了比较丰富的研究成果,但是仍然存在不少值得深入研究的课题.比如,基于一般三角模的模糊逻辑形式系统仍然有待建立;又如,模糊逻辑的形式系统已经有很多,那么这些系统的比较与选择问题,也有待深入的讨论;另外,与经典逻辑相比,许多模糊逻辑系统的逻辑性质还需要更深入的研究.

关于模糊推理的合理性问题,这是一个十分紧迫的研究课题.在这方面的研究已经有一些文献涉及.比如:模糊推理的扰动或鲁棒性问题研究[72-77]、模糊推理连续性研究[78,44]、基于重言式的模糊推理方法研究[79]、基于计量逻辑学的模糊推理研究[80],以及模糊推理逻辑基础的研究[46-47]等.自然地,考虑基于相似度的模糊推理方法[81-82]的合理性问题也是有重要意义的.

关于模糊量词的研究,主要有:带有模糊量词的逻辑系统研究[83]、量化命题的模糊推理研究[84]等.

关于模糊推理的应用研究,我们知道,逻辑的核心问题是推理,而推理的真正价值在于应用.模糊推理的主要应用领域有:模糊逻辑控制、模糊专家系统、模糊决策分析,以及模糊关系方程[49-54,85-86]等.

4 结论

本文简要地介绍了最近30年来模糊逻辑研究的主要成果,就学术界关注的几个问题展开了论述,这些问题包括:模糊逻辑的重要性、早期模糊逻辑的主要缺陷、现代模糊逻辑的主要成就,以及未来模糊逻辑的几个发展方向.

值得指出的是,以上论述仅仅反映了笔者的见解,而且只限于笔者比较熟悉的狭义模糊逻辑的几个研究领域,很难保证没有遗漏,也可能存在偏见,欢迎国内外同行专家提出宝贵的批评意见.

[1] 王宪钧. 数理逻辑引论[M]. 北京:北京大学出版社,1998.

[2] 王国俊. 非经典数理逻辑与近似推理[M]. 2版. 北京:科学出版社,2008.

[3] 王国俊. 数理逻辑引论与归结原理[M]. 2版. 北京:科学出版社,2006.

[4] 裴道武. 基于三角模的模糊逻辑理论及其应用[M]. 北京:科学出版社,2013.

[5] ZADEH L A. Fuzzy sets[J]. Inform Cont,1965,8:338-353.

[6] MARINOS P N. Fuzzy logic and its application to switching systems[J]. IEEE Trans Comput,1969,18:343-348.

[7] KANDEL A. On minimization of fuzzy functions[J]. IEEE Trans Comput,1973,22(9):826-832.

[8] MUKAIDONO M. On some properties of fuzzy logic[J]. Syst Comput Cont,1975,6:36-43.

[9] ZADEH L A. Outline of a new approach to the analysis of complex systems and decision process[J]. IEEE Trans S M C,1973,1(1):28-44.

[10] ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning:Part 1～3[J]. Inform Sci,1975,8:199-249,301-357;9:43-80.

[11] DUBOIS D, PRADE H. Fuzzy sets in approximate reasoning (I,II)[J]. Fuzzy Sets Syst,1991,40(2):143-244.

[12] MAMDANI E H. Applications of fuzzy algorithms for simple dynamic plant[J]. Proc IEE,1974,121:1585-1588.

[13] MAMDANI E H, ASSILIAN S. An experiment in linguistic synthesis with a fuzzy logic controller[J]. Int J Man Mach Studies,1975,7:1-13.

[14] PAVELKA J. On fuzzy logic (I;II;III)[J]. Z Math Logik Grundl Math,1979,25:45-52,119-134,447-464.

[16] ELKAN C. The paradoxical success of fuzzy logic[J]. IEEE Expert,1994,9(4):3-8.

[17] 吴望名. 关于模糊逻辑的一场争论[J]. 模糊系统与数学,1995,9(2):1-9.

[18] ZADEH L A. Why the success of fuzzy logic is not paradoxical[J]. IEEE Expert,1994,9(4):47-49.

[19] 裴道武. 关于模糊逻辑与模糊推理逻辑基础问题的十年研究综述[J]. 工程数学学报,2004,21(2):249-258.

[21] 王国俊. 模糊逻辑与模糊推理[C]//全国第七届多值逻辑与模糊逻辑学术会议论文集,1996:82-96.

[22] 王国俊. Fuzzy命题演算的一种形式演绎系统[J]. 科学通报,1997,42(10):1041-1045.

[23] 王国俊. 蕴涵格与Stone表现定理的推广[J]. 科学通报,1998,43(10):1033-1036.

[24] WANG G J. On the logic foundation of fuzzy reasoning[J]. Inform Sci,1999,117(1):47-88.

[25] 裴道武,王国俊. 形式系统L*的完备性及其应用[J]. 中国科学,2002,E32(1):56-64.

[27] WANG S M. A fuzzy logic for the revised drastic productt-norm[J]. Soft Comput,2007,11:585-590.

[28] WANG S M, WANG B S, WANG G J. A triangular-norm-based propositional fuzzy logic[J]. Fuzzy Sets Syst,2003,136:55-70.

[29] WANG S M, WANG B S, WANG G J. A triangular norm-based fuzzy predicate logic[J]. Fuzzy Sets Syst,2003,138:177-186.

[30] GOTTWALD S. A Treatise on Many-Valued Logics[M]. Baldock:Research Studies Press LTD,2001.

[31] KLEMENT E P, MESIAR R, PAP E. Triangular Norms[M]. Dordrecht:Kluwer,2000.

[32] CIGNOLI R, ESTEVA F, GODO L, et al. Basic fuzzy logic is the logic of continuoust-norms and their residua[J]. Soft Comput,2000,4:106-112.

[33] ESTEVA F, GODO L. Monoidalt-norm based logic:towards a logic for left-continuoust-norms[J]. Fuzzy Sets Syst,2001,124:271-288.

[34] JENEI S, MONTAGNA F. A proof of standard completeness for Esteva and Godo’s logic MTL[J]. Studia Logica,2002,70:183-192.

[35] PEI D W. On equivalent forms of fuzzy logic systems NM and IMTL[J]. Fuzzy Sets Syst,2003,138(1):187-195.

[37] METCALFE G, MONTAGNA F. Substructural fuzzy logics[J]. J Symbol Logic,2007,7(3):834-864.

[38] XU Y, RUAN D, QIN K, et al. Lattice-Valued Logic[M]. Berlin:Springer-Verlag,2003.

[39] 王国俊. 模糊推理的全蕴涵三I算法[J]. 中国科学,1999,E29(1):43-53.

[40] 王国俊,刘华文,宋建社. 三I方法综述[J]. 模糊系统与数学,2006,20(6):1-14.

[41] PEI D W. The unified algorithms of triple I methods for fuzzy reasoning[J]. Inform Sci,2008,178(2):520-530.

[42] WANG G J, FU L. Unified forms of triple I method[J]. Comput Math Appl,2005,49:923-932.

[43] TANG Y M, LIU X P. Differently implicational universal triple I method of (1,2,2) type[J]. Comput Math Appl,2010,59(6):1965-1984.

[44] LIU H W, WANG G J. Continuity of triple I mehtods based on several implications[J]. Comput Math Appl,2008,56(8):2079-2087.

[45] 裴道武. 一阶形式系统K*及其完备性[J]. 数学年刊,2002,23(6):675-684.

[46] PEI D W. On the strict logic foundation of fuzzy reasoning[J]. Soft Comput,2004,8(8):539-545.

[47] PEI D W. Formal triple I methods based on monoidalt-norm based logic[J]. Int J Approx Reason,2012,53(5):837-846.

[48] 宋士杰,吴澄. 模糊推理的反向三I算法[J]. 中国科学,2002,E32(2):230-246.

[49] 李洪兴. 常见模糊蕴涵算子的模糊系统及其响应函数[J]. 控制理论与应用,2005,22(3):341-347.

[50] 李洪兴. Fuzzy系统的概率表示[J]. 中国科学,2006,E36(4):373-397.

[51] 李洪兴,彭家寅,王加银,等. 基于三I算法的模糊系统及其响应性能[J]. 系统科学与数学,2006,25(5):578-590.

[52] 李洪兴,尤飞,彭家寅,等. 基于某些模糊蕴涵算子的模糊控制器及其响应函数[J]. 自然科学进展,2003,13(10):1073-1077.

[53] 潘海玉,裴道武,陈仪香. 基于三I算法的模糊系统的响应能力[J]. 控制理论与应用,2011,28(1):24-30.

[54] WANG D G, MENG Y P, LI H X. A fuzzy similarity inference method for fuzzy reasoning[J]. Comput Math Appl,2008,56:2445-2454.

[55] WANG G J, WANG H. Non-fuzzy versions of fuzzy reasoning in classical logics[J]. Inform Sci,2001,138:211-236.

[56] 王国俊. 修正的Kleene系统中的Σ-(α-重言式)理论[J]. 中国科学,1998,E28(2):146-152.

[57] 王国俊,傅丽,宋建社. 二值命题逻辑中命题的真度理论[J]. 中国科学,2001,A31(11):998-1008.

[58] WANG G J, LEUNG Y. Integrated semantics and logic metric spaces[J]. Fuzzy Sets Syst,2003,136:71-91.

[59] 王国俊. 计量逻辑学(I)[J]. 工程数学学报,2006,23(2):191-215.

[60] WANG G J, ZHOU H J. Quantitative logic[J]. Inform Sci,2009,179:226-247.

[61] 惠小静,王国俊. 经典推理模式的随机化研究及其应用[J]. 中国科学,2007,E37(6):801-812.

[64] WANG G J, ZHANG W X. Consistency degrees of finite theories inukasiewicz propositional fuzzy logic[J]. Fuzzy Sets Syst,2005,149:275-284.

[65] 王国俊. 计量逻辑学的基本思想与研究综述[J]. 模糊系统与数学,2012,26(4):1-11.

[66] 周红军. 概率计量逻辑及其应用[M]. 北京:科学出版社,2015.

[67] BACZYNSKI M, JAYARAM B. Fuzzy Implications[M]. Berlin:Springer-Verlag,2008.

[68] QIN F, BACZYNSKI M, XIE A. Distributive equations of implications based on continuous triangular norms (I)[J]. IEEE Trans Fuzzy Syst,2012,20:153-167.

[70] CIGNOLI R, D’OTTAVIANO I M L, MUNDICI D. Algebraic Foundations of Many-valued Reasoning[M]. Dordrecht:Kluwer Academic Publishers,1999.

[71] 张小红. 模糊逻辑及其代数分析[M]. 北京:科学出版社,2008.

[72] LI Z. Suitability of fuzzy reasoning methods[J]. Fuzzy Sets Syst,1999,108:299-311.

[73] YING M S. Perturbation of fuzzy reasoning[J]. IEEE Trans Fuzzy Syst,1999,7:625-629.

[74] CAI K Y. Robustness of fuzzy reasoning andδ-equalities of fuzzy sets[J]. IEEE Trans Fuzzy Syst,2001,9(5):738-750.

[75] LI Y M, LI D C, PEDRYCZ W, et al. An approach to measure the robustness of fuzzy reasoning[J]. Int J Intel Syst,2005,20(4):393-413.

[76] CHENG G S, FU Y X. Error estimation of perturbations under CRI[J]. IEEE Trans Fuzzy Syst,2006,14(6):709-715.

[77] DAI S S, PEI D W, WANG S M. Perturbation of fuzzy sets and fuzzy reasoning based on the normalized Minkowski distances[J]. Fuzzy Sets Syst,2011,189:63-73.

[78] JENEI S. Continuity on Zadeh’s compositional rule of inference[J]. Fuzzy Sets Syst,1999,104:333-339.

[79] PEI D W, YANG R. Hierarchical structure and applications of fuzzy logical systems[J]. Int J Approx Reason,2013,54(9):1483-1495.

[80] PEI D W, ZHANG A Y. Truth degree analysis of fuzzy reasoning[J]. J Intel Fuzzy Syst,2014,26:1439-1452.

[81] TURKSEN I B, TIAN Y. Combination of rules or their consequences in fuzzy expert systems[J]. Fuzzy Sets Syst,1993,58:3-40.

[82] TURKSEN I B, ZHONG Z. An approximate analogical reasoning approach based on similarity measures[J]. IEEE Trans Syst, Man Cybern,1988,18(6):1049-1056.

[83] YING M S. Linguistic quantifiers modeled by Sugeno integrals[J]. Artif Intel,2006,170:581-606.

[84] 吴望名. 模糊推理的原理和方法[M]. 贵阳:贵州科技出版社,1994.

[85] ZADEH L A. The role of fuzzy logic in the management of uncertainty in expert systems[J]. Fuzzy Sets Syst,1983,11:199-227.

[86] WANG X P, ZHAO S. Solution sets of finite fuzzy relation equations with sup-inf composition over bounded Brouwerian lattices[J]. Inform Sci,2013,234:80-85.

2010 MSC:03B50; 03B52; 68T27; 68T37

(编辑 余 毅)

Some Problems and Advances of Fuzzy Logic

PEI Daowu

(SchoolofSciences,ZhejiangSci-TechUniversity,Hangzhou310018,Zhejiang)

In the past thirty years, a great development has been done for fuzzy logic in both theory and application. Up to today, there still are some interesting directions and topics which are wirthy of further research. In this paper, we discuss some advances about the four problems: Why is fuzzy logic necessary? What shortcomings are there in the old fuzzy logic? What main results are there in the modern fuzzy logic? Where will fuzzy logic go in the future?

fuzzy logic; T-norm; R-implication; quantitative logic; fuzzy reasoning

2016-12-26

国家自然科学基金(11171308、61379018和61472471)

裴道武(1956—),男,教授,主要从事模糊逻辑与近似推理的研究,E-mail:peidw@163.com

O141.1

A

1001-8395(2017)03-0411-08

10.3969/j.issn.1001-8395.2017.03.023