叠合梁的叠合面及斜截面抗剪效应特征分析★

姜 宇 丁圣果

(1.贵州省城乡规划设计研究院,贵州 贵阳 550003； 2.贵州大学土木建筑工程学院，贵州 贵阳 550025)



叠合梁的叠合面及斜截面抗剪效应特征分析★

姜 宇1丁圣果2

(1.贵州省城乡规划设计研究院,贵州 贵阳 550003； 2.贵州大学土木建筑工程学院，贵州 贵阳 550025)

基于无腹筋梁叠合面剪应力理论，分析了受弯构件叠合面的抗剪承载力，并将国内外对无腹筋梁(板)斜截面混凝土抗剪承载力的规范要求进行了比较，为我国相关规范的修订提供参考。

叠合面，剪应力，承载力，混凝土构件

0 引言

在既有建筑加固改造工程中，梁、板常采用增大截面加固，在装配式建筑工程中,二次现浇的叠合楼盖板应用也颇为频繁。根据现行规范[1]中有关弯曲叠合构件抗剪的设计规定，并结合我们的加固工程经验，应用经典材料力学理论对混凝土叠合梁进行了计算分析，并总结这类梁在弯、剪状态的效应特征。

1 基本假设

1)平截面假设，梁弯曲变形后的截面仍保持平面;2)内力及变形遵循弹性规律，对无腹筋梁抗剪按材料力学理论分析。

2 叠合面的抗剪分析

2.1 无腹筋梁叠合面剪应力理论分析

对于无腹筋叠合梁、板构件，按材料力学理论分析正截面剪应力计算式为：

(1)

根据剪应力互等定侓，该式也是距中性轴y处叠合面的剪应力(见图1)。

代入式(1)可计算得叠合面处剪应力：

(2)

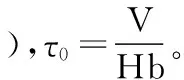
(3)

2.2 受弯构件叠合面抗剪承载力比较

按现行规范[1]对板叠合面抗剪强度条件为：

(4)

对于叠合梁混凝土的叠合面抗剪强度条件为：

(5)

我国现行规范[1]对叠合面受剪承载力计算式(4)，式(5)是以摩擦传力模型为基础，根据叠合构件试验结果和剪切摩檫试验结果给出的，式(4)暂不与混凝土强度等级挂勾，是考虑为今后将集中力与分布力引起的抗剪承载力公式统一的后继发展研究留有余地，是一个过渡性公式。而加固规范[2]对叠合面抗剪未作明确规定。

无论是叠合梁或叠合板，设置垂直于叠合面拉结筋的做法从构造要求上是必要的。对于加固梁，在原梁箍上逐一焊接延伸到叠合层内，一般能达到这一构造要求。但对于叠合板，规范[1]仅在9.5.2.2条中对承受较大荷载板提出宜在预制底板上设置伸入叠合层的构造钢筋，文献[3]也要求垂直于叠合面植入φ6@600构造筋。但根据本文前面的分析， 板加厚截面的加固工程中有可能造成剪力较大的板边叠合层抗剪薄弱。这种新旧混凝土间的拉结不仅能显著提高组合构件的抗弯承载力，且拉结钢筋的销钉作用对叠合面的抗剪承载力贡献也是十分重要的。美国规范[4]在摩擦抗剪设计方法的11.7.4.1条中明确给出摩擦抗剪所需垂直于剪切面钢筋量：

(6)

其中，Vn为名义剪力； fy为钢筋屈服强度设计值；μ为摩擦系数,按规范[4]要求：μ=0.6λ，φ=0.75。对于常规板[7]，取Vn=(0.4～1.1)×105N，试按式(6)计算叠合面所需HPB300拉结筋，计算得每米板宽新、旧混凝土间拉结筋：Avf=(0.4～1.1)×74.074mm2，相当于φ6@100～φ12@100。我国规范[1,2]对新旧混凝土之间的拉结未提出定量标准。根据我们在众多板加固工程中的经验总结，建议板叠合层植入φ6@100～200梅花布置的拉结筋。

3 国内外对无腹筋梁(板)斜截面混凝土抗剪承载力的比较

与欧美规范的比较。我国规范[1]对受弯构件的剪切抗力项是分混凝土和腹筋的贡献分列的,无腹筋梁的混凝土抗剪切应力为：

fcu=0.7βhft

(7)

fuc=ck(100ρlfck)1/3

(8)

按美国规范[4],斜截面混凝土抗剪切应力为:

(9)

表1给出按式(7)～式(9)计算得出的斜截面抗剪许容应力比较。

表1 不同规范斜截面抗剪应力比较

式(8)及式(9)表现出欧美规范对混凝土梁板斜截面抗剪强度与纵筋配筋率、混凝土强度等级、构件可靠度、截面高度的相关性。相对于按欧、美规范，我国规范计算的混凝土剪切抗力值大11%～30%,表现出国外规范较国内具有更高的安全储备。事实上，由于受弯构件受剪破坏的因素较多，破坏形态复杂，至今对混凝土构件受剪破坏的机理认识尚不充分，未能像正截面承载力计算一样建立完整的理论体系。图2给出欧规范1992-1-1∶2004的无腹筋抗剪强度频率分布的试验结果统计[7]，表现出受弯构件抗剪承载力离散性较大特点。

4 结论

2)在加固工程中，无论是叠合梁或叠合板，在叠合面设置垂直于叠合面拉结筋是必要的构造措施，这一措施不仅能有效提高叠合面摩擦抗剪性能，且对有效提高正截面抗弯、斜截面抗剪性能也是十分必要的。

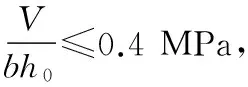
4)无腹筋受弯构件斜截面上混凝土的抗剪强度不仅与混凝土强度相关，尚与纵筋配筋率、截面高度、构件可靠度、剪跨比等因素相关。

5)欧洲规范与美国规范计算的无腹筋受弯构件的混凝土斜截面抗剪强度较为接近，且均显著小于我国现行规范对斜截面混凝土抗剪强度的限值：fuc=0.7βhft。

[1]GB50010—2010，混凝土结构设计规范[S] .

[2]GB50367—2013，混凝土结构加固设计规范[S].

[3]TU370.4/46,混凝土结构加固构造图集[M].北京：中国电力出版社,2008.

[4]ACI318M-05，Buldingcoderequirementsforstructuralconcreteandcommentary[S].

[5] 贡金鑫,车 轶,李荣庆.混凝土结构设计:按欧洲规范[M].北京：中国建筑工业出版社，2009.

[6]Exampleforthedesignofconcretebuildings.basedonpublicationDDENV1992-1-1:1992Eurocode2 .publishedbybritithcementAssociationOVEApruandpartenerandS.BTietzpartener.

[7] 黄菊华, 钱应平, 李厚民.不同形式叠合梁的应力分析[J].湖北工业大学学报,2008,23(6)：3.

Analysis of shear effect of superposition surface for superposition beam★

Jiang Yu1Ding Shengguo2

(1.Urban and Rural Planning and Design Institute of Guizhou Province, Guiyang 550003, China; 2.College of Civil Engineering of Guizhou University, Guiyang 550025, China)

Based on the non-reinforced beam superposition shear theory, the paper analyzes the shear loading capacity of the superposition of the bended component, and compares the shear loading capacity of the non-reinforced beam inclined section concrete at home and abroad, so as to provide some reference for the related regulations in China.

superposition, shearing stress, loading capacity, concrete component

1009-6825(2017)08-0037-03

2017-01-06★：贵州省科学技术基金项目(合同编号：黔科合J字[2011]2014号)

姜 宇(1979- )，男，硕士，工程师，国家一级注册结构工程师； 丁圣果(1947- )，男，硕士，教授

TU311

A