针织物冷轧堆染色收卷张力设计
尹苗苗, 岳晓丽, 钟 毅, 陈慧敏
(1. 东华大学 机械工程学院, 上海 201620; 2. 东华大学 生态纺织教育部重点实验室, 上海 201620)
针织物冷轧堆染色收卷张力设计
尹苗苗1, 岳晓丽1, 钟 毅2, 陈慧敏1
(1. 东华大学 机械工程学院, 上海 201620; 2. 东华大学 生态纺织教育部重点实验室, 上海 201620)
为解决冷轧堆染色收卷过程中因缝头而导致的染色色差问题,以针织物为研究对象,分析缝头印产生机制,利用厚壁筒原理和数值迭代计算方式,对针织物的收卷过程进行力学分析,建立针织物收卷张力数学模型。分析等张力收卷和锥度收卷下,剩余缠绕张力值和径向压力值的变化曲线,以控制缝头印为目标,兼顾针织物的卷形,建立幂函数收卷张力模型。研究表明:幂函数收卷方式下的径向压力值远小于等张力收卷和锥度收卷,且幂函数的指数越小,剩余缠绕张力分布越均匀,径向压力值越小,有利于控制缝头印的产生,获得高质量染色织物,为针织物冷轧堆染色机的张力设计提供参考。
缝头印; 收卷张力; 冷轧堆染色; 针织物
冷轧堆染色是将织物在低温下浸轧染液和碱液,利用轧辊压轧使染液吸附在纤维表面,然后进行打卷,在室温下堆置固色,最后水洗完成上染的染色工艺[1]。该染色工艺具有节约能源、污染小、固色率高等特点,但也容易产生缝头印,影响织物染色质量。为了生产的连续性,经常需要对布匹进行缝合。由于缝合处的织物厚度不一致,在机械作用下,常会造成该处染色不均。在后续的打卷堆置中,缝头处往往会连续通过数层,产生缝头印,造成织物相当多的横档疵点,成为影响产品质量的主要问题,也增加了生产成本[2]。影响缝头印的因素有很多,如缝头质量、卷绕张力、径向压力、活性染料等。现有预防缝头印产生的措施有:将对接处尽量拉开,采用包缝机对接缝头,降低接缝处的厚度;在缝头处添加塑料薄膜,改善上下层间泳移现象;采用主动打卷,降低打卷张力等[3]。这些预防措施耗费大量的人力物力,并不能从根本上解决缝头印问题。
本文分析了缝头印产生的原因,然后根据弹性力学厚壁筒理论,考虑收卷过程中卷筒的离心惯性力,推导出收卷过程中织物的受力变化,建立收卷张力模型,为控制缝头印提供理论参考。
1 缝头印产生机制
在连续式冷轧堆染色中,为保证放卷的连续性,需将布匹之间通过缝纫车缝接在一起,缝头处布头折叠不平,厚度大于正常部位,如图1所示。
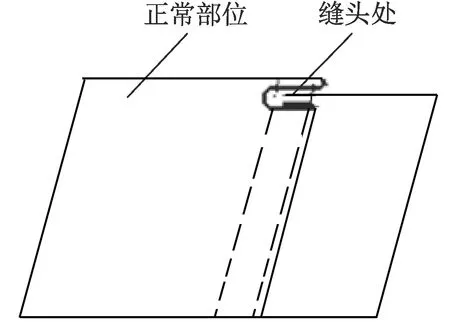
图1 缝头示意图Fig.1 Diagram of seam
浸染染液时,缝头处带液量多;通过轧辊后,缝头处由于厚度大,所受压力高于正常部位,染液更容易挤压出来;堆置过程中,织物整体所受的压力较小,正常部位以及相邻布层的染液向缝头布的接缝迁移(如图2所示),最终导致缝头位置上下数层与正常布面的带液量不同,造成缝头印[3],因此,缝头印的形成与织物所受压力密切相关。
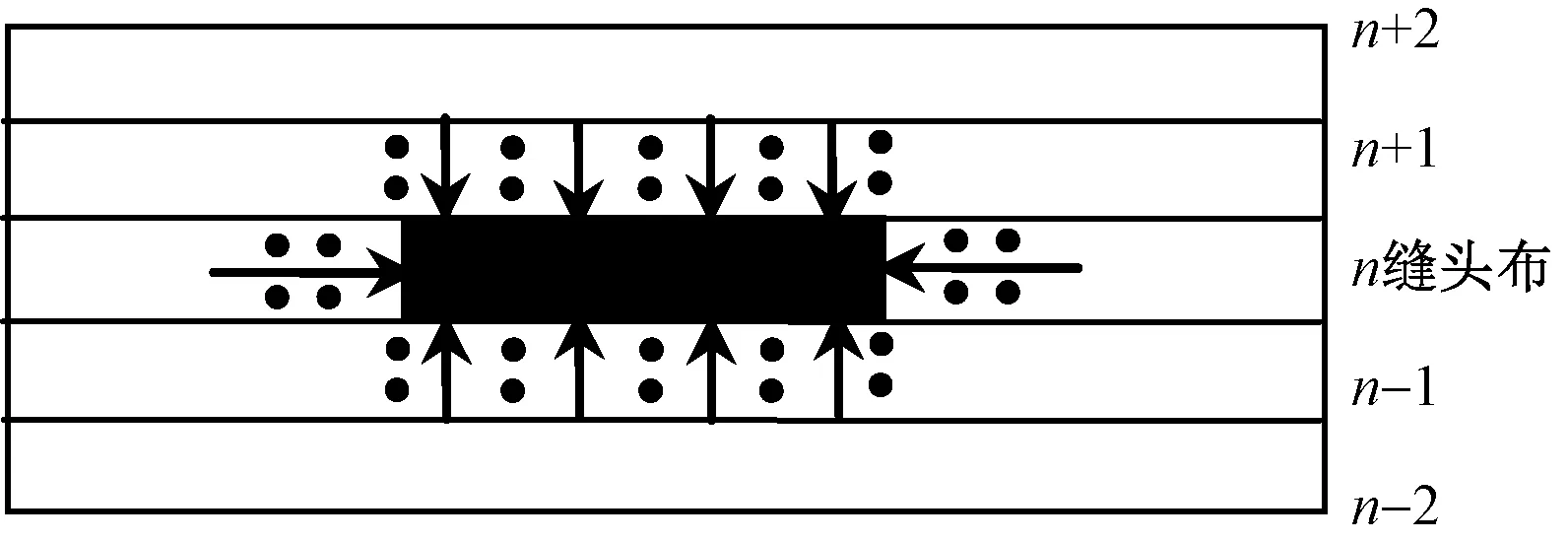
图2 染液迁移示意图Fig.2 Diagram of dye transfer
2 收卷筒基本方程
因织物有一定宽度,收卷后暂不考虑纬向变形,将布卷简化为轴对称平面应变问题。收卷辊刚度相对织物的刚度大很多,可近似认为刚体[4]。根据厚壁筒理论,将布卷看成是一个由多层织物卷绕成的厚壁圆筒。卷绕过程中,卷筒的内壁由收卷辊支撑,外壁受到新卷进来的织物挤压[5]。图3示出收卷筒的受力分析。其中,将收卷模型简化为外半径为R的宽带环向缠绕在外半径为R0的收卷辊圆筒上,外层宽带上施加均匀环向外压P,如图3(a)[6]所示。
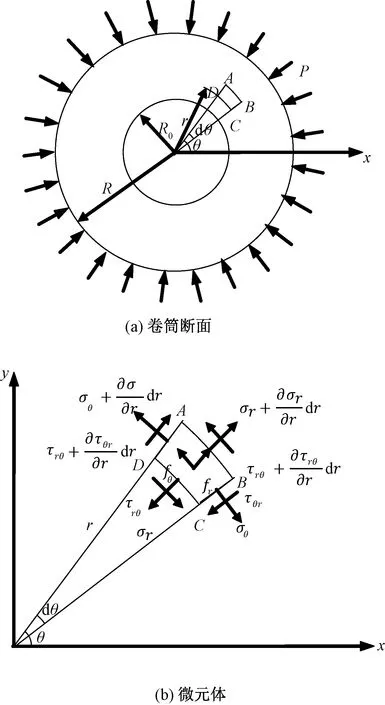
图3 受力分析Fig.3 Mechanical analysis. (a) Cross section of model; (b) Micro cell of cross section
取出厚壁圆筒上的微小单元ABCD,对其进行受力分析,其应力分量如图3(b)所示,其中fr和fθ分别为r、θ方向的体力分量,σr和σθ分别为r、θ方向的正应力,τθr和τrθ分别为r、θ方向的切应力[7]。
2.1 受力分析
对图3(b)中的微小单元ABCD列出径向平衡方程:
(1)
在轴对称平面应变问题中,切应力τrθ=τθr=0。
径向和切向的应变分别用εr和εθ表示,与径向位移u满足几何方程:
(2)
(3)
针织物是由纱线顺序弯曲成线圈,线圈相互串套形成织物,因此针织物具有良好的弹性和松软度,对应力敏感,可产生较大变形。针织物各向异性本构方程[8]为:
(4)
(5)
式中:Er、Eθ分别为r、θ方向的弹性模量;vr、vθ分别为r、θ泊松比。
联立上述方程式,求得关于径向正应力σr的微分方程:
(6)
由于收卷后布卷在单位体积上受到离心惯性力,大小为fr=ρω2r,式中:ρ为织物密度,ω为收卷辊转动角速度。

(7)
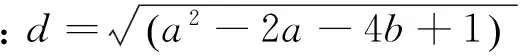
将径向应力σr的通解代入式(1)、(2)、(4)、(5),得到周向应力σθ和径向位移u的表达式,均是关于r、C1和C2的函数,即:
σθ=f1(r,C1,C2)
(8)
u=f2(r,C1,C2)
(9)
2.2 边界条件
收卷辊刚度远大于织物,可认为收卷辊外径R0(即织物收卷筒内径)处径向位移u为零;收卷筒外壁R处径向应力σr为P。边界条件可表示为
u|r=R0=0;σr|r=R=-P
将边界取值代入式(8)和式(9),用待定系数法可求解出C1和C2值。
3 收卷张力模型设计
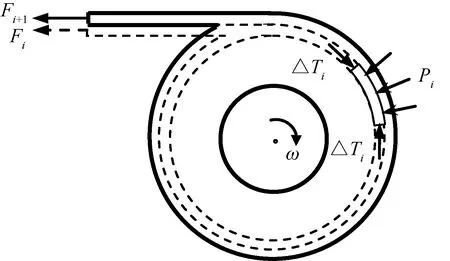
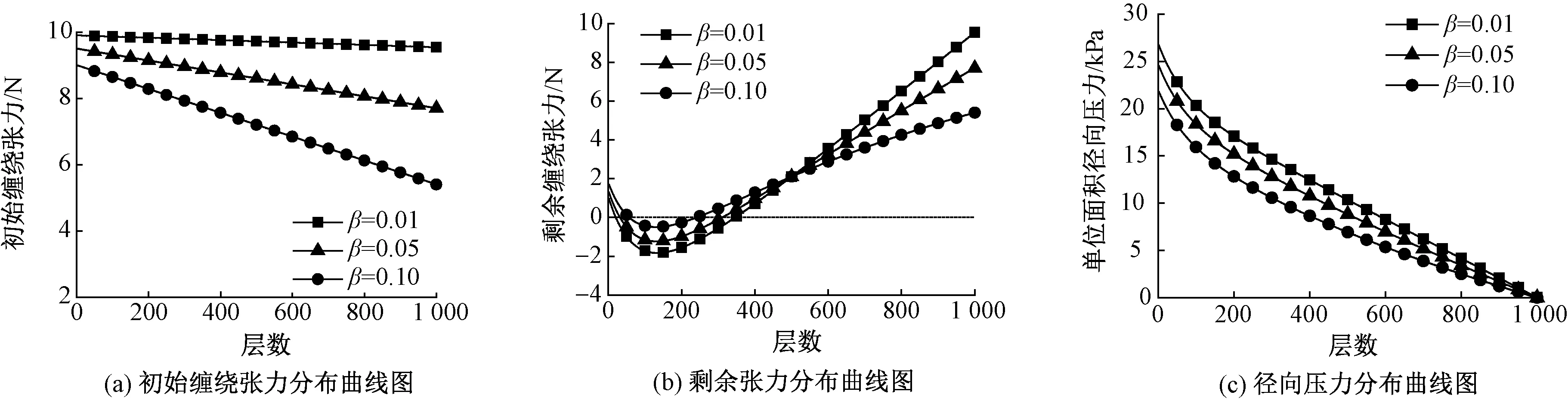
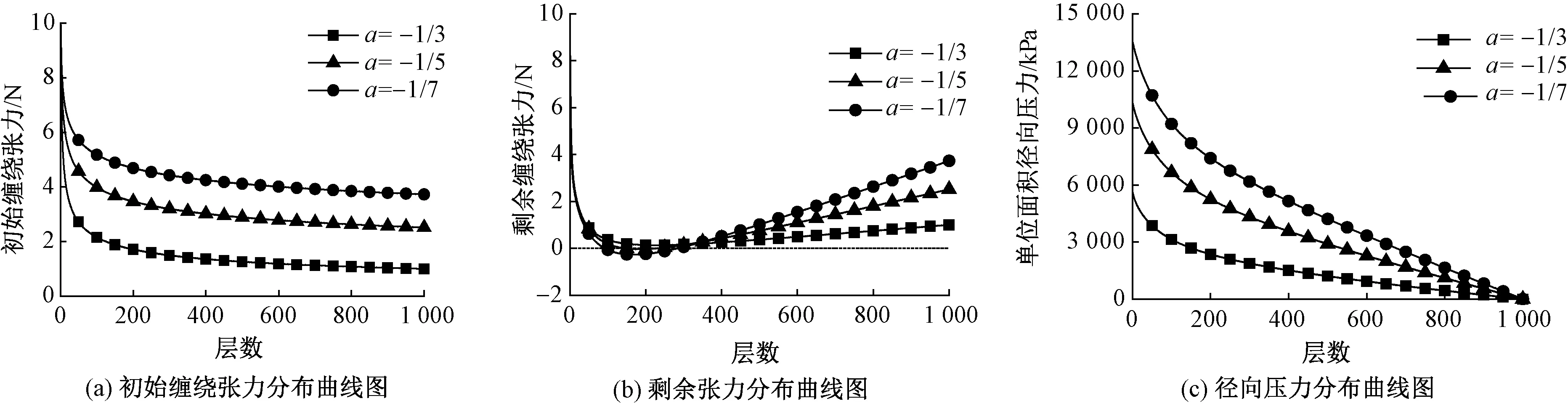
与收卷过程相关的张力值有3个:一是初始缠绕张力Fi(n为布卷最终卷绕层数;i为卷绕层标号,i=1,2,…,n,如图4所示),指收卷筒收卷到第i层时,作用在外层(即第i层)单位宽度织物上的张力;二是剩余缠绕张力Ti(i 图4 卷绕层数示意图Fig.4 Diagram of winding layer 3.1 初始缠绕张力与剩余缠绕张力分析 缠绕张力示意图如图5所示。当某层织物作为最外层时,不受外层织物的压力作用,此时该层织物所受张力为初始缠绕张力Fi;收卷辊以角速度ω继续卷绕,此时,该层织物不再是最外层,它受到上一层织物的径向压力Pi,外层径向压力Pi将会导致该层产生张力放松量△Ti,此时该层的剩余张力等于初始缠绕张力Fi减去上一层织物施加的径向压力引起的张力放松量△Ti。 图5 缠绕张力示意图Fig.5 Diagram of tension 随着收卷过程的进行,收卷层数i和收卷筒半径r不断增大,剩余张力和径向压力也会不断改变。收卷过程中,每新收卷一层织物,该层(即第i+1层)织物张力就会对前面一层(即第i层)已收卷织物产生径向压力,导致第i层剩余张力减小,影响i-1层已收卷织物所受径向压力,造成第i-1层剩余张力减小。同样,第i-1层剩余张力的减小又会改变第i-2层的剩余张力,最终新收卷的织物会改变收卷筒的每一层剩余张力。 3.2 张力放松量分析 记收卷筒第i层织物的内半径为ri-1,外半径为ri,ri=ri-1+s,其中s为织物厚度。假设收卷筒已经卷到第n层,以收卷筒第i层织物为研究对象,第i层织物受上层织物(即第i+1层)的径向压力,引起当层织物产生张力放松量。张力的放松量可由周向应力求出,即△Ti=s×σθ。根据式(8)可知,张力放松量△Ti也是关于ri-1、C1和C2的函数,其中C1和C2根据ur=R0=0;σr=ri=-Pi求解出,因此,张力放松量△Ti可表示为: △Ti=f3(i,Pi) (10) 3.3 剩余缠绕张力分析 若收卷筒已经卷到第n层,取第i层中的微小弧段单元进行受力分析,结果如图6所示。 图6 微小弧段单元受力分析图Fig.6 Force diagram of micro arc 该层织物径向方向受上一层,即第i+1层织物对其施加的压力Pi和下一层对其施加的支撑力Pi-1,织物周向承受张力Ti,根据达朗贝尔原理列出平衡方程: (11) ma=rθsρω2ri-1 (12) 式中:m为微单元的质量,a为微单元的加速度。 当θ足够小时,sinθ≈θ,联立式(11)和式(12)可得第i-1层的径向压力: (13) 可见,第i-1层的径向压力Pi-1是关于i-1、Ti和Pi的函数,即: Pi-1=P(i-1,Ti,Pi) (14) 第i-1层的张力放松量为 △Ti-1=△T(i-1,Pi-1) (15) 第i-1层的剩余缠绕张力为 Ti-1=Fi-1-△Ti-1 (16) 第n层(即最外层)时,Pn=0,Tn=Fn-△Tn=Fn-△T(n,0)。 当布卷最终卷绕的层数为n层时,卷筒内任意r处的剩余缠绕张力可通过迭代法求解,即最外层n层的径向压力与剩余张力作为第n-1层径向压力与剩余缠绕张力的求解条件,求解出的第n-1层径向压力与剩余缠绕张力继续作为第n-2层径向压力与剩余缠绕张力的求解条件,直到求解出最内层的径向压力与剩余缠绕张力值,从而得到布卷内的径向压力与剩余缠绕张力分布。求解过程如下: 对于最外层n,Pn=0,Tn=Fn-△T(n,0); 对于第n-1层,Pn-1=P(n-1,Tn,Pn),Tn-1=Fn-1-△T(n-1,Pn-1); 对于第n-2层,Pn-2=P(n-2,Tn-1,Pn-1),Tn-2=Fn-2-△T(n-2,Pn-2); …… 对于第1层,P1=P(1,T2,P2),T1=F1-△T(1,P1)。 剩余缠绕张力的值直接影响布卷的卷形:若剩余缠绕张力过大,容易造成织物撕裂;若剩余缠绕张力过小,甚至小于零,会造成织物内部产生折皱。径向压力的值影响缝头印的层数:若径向压力过大,造成缝头印层数多,染色质量差,因此,本节计算了不同收卷方式下的剩余缠绕张力和径向压力分布,并提出新的收卷方式,以兼顾布卷卷形和控制缝头印的产生。 根据文献[10]给出的针织物力学性能参数,计算布卷最终卷绕层数为1 000层(即最终所卷织物长约1 800 m,布卷直径为0.92 m)情况下,剩余缠绕张力和径向压力分布。具体的计算参数如表1所示。 表1 计算参数表Tab.1 Calculation parameter table 4.1 等张力收卷 在针织物冷轧堆染色工艺中,每米幅宽承受张力为10 N时可保证安全传送[11]。故令等张力收卷方式的初始缠绕张力F=10 N,根据收卷张力模型计算可得剩余缠绕张力和层间压力曲线,见图7。 由图可知,采用等张力收卷时,剩余缠绕张力随着层数增加先减小后增大。织物越靠近收卷辊,剩余缠绕张力值越小,且在20~350层范围内,剩余缠绕张力的值小于零,容易出现折皱;织物越靠近外层,剩余缠绕张力值越大。图7(b)示出,单位面积径向压力随着层数增加不断减小,织物靠近收卷辊处径向压力最大,约为27 kPa,不利于缝头印的控制。 4.2 锥度收卷 锥度收卷是指初始缠绕张力随着收卷半径增大而线性减小的收卷方式,其数学表达式为 其中T0=10 N,β为锥度系数,分别取0.01、0.05、0.10[12]。根据收卷张力模型计算锥度收卷下的剩余缠绕张力和层间压力分布曲线,如图8所示。 图7 等张力收卷曲线图Fig.7 Curve under constant wingding tension. (a) Residual tension distribution; (b) Radial pressure distribution 图8 锥度收卷曲线图Fig.8 Curve under taper wingding tension. (a) Winding tension distribution; (b) Residual tension distribution; (b) Radial pressure distribution 图9 幂函数收卷曲线图Fig.9 Curve under power function wingding tension. (a) Winding tension distribution; (b) Residual tension distribution; (c) Radial pressure distribution 由图8可知,采用锥度收卷时,剩余缠绕张力和径向压力变化趋势与等张力收卷基本相同。锥度系数β值越小,越接近等张力收卷;锥度系数β值越大,剩余缠绕张力小于零值的数据点越少,不容易出现折皱;此时单位面积径向压力值整体减小,有利于缝头印的控制。 4.3 幂函数收卷 图9示出幂函数收卷曲线图。在收卷过程中,以控制缝头印为目标,要求最大径向压力值越小越好,同时兼顾布卷卷形,即最小剩余缠绕张力大于零,提出幂函数收卷,即初始缠绕张力为幂函数形式,其数学表达式为F=T0iα,其中T0=10 N,i为层数,α为指数。图9(a)示出α值分别取-1/3、-1/5、-1/7时的初始缠绕张力分布曲线。根据收卷张力模型,计算幂函数收卷下的剩余缠绕张力和层间压力分布曲线,如图9(b)、(c)所示。 由图9可知,采用幂函数收卷时,指数α值为-1/3时,剩余缠绕张力分布均匀,且剩余缠绕张力值基本都大于零,布卷内部不容易出现折皱;此时,单位面积径向压力大幅度减小,其最大值为5 580Pa,远小于等张力和锥度收卷的径向压力值,有利于控制缝头印的产生。 为解决针织物冷轧堆染色缝头印问题,分析不同收卷方式下的剩余缠绕张力和单位面积径向压力分布。根据厚壁筒原理和数值迭代法,以控制缝头印为目标,兼顾针织物的卷形,建立针织物收卷张力模型,揭示收卷过程中的张力和压力变化规律,得到以下结论。 1)等张力收卷下,内层剩余张力小于零的数据点最多,易发生折皱,影响布卷的卷形;锥度收卷下,剩余缠绕张力差值随着锥度系数增大而减小,且内层最小张力随着锥度系数增大而增大,可以有效减少折皱的产生;幂函数收卷下,随着指数的减小剩余张力分布均匀,且最小剩余张力大于零,可以避免发生折皱,保证布卷卷形。 2)等张力收卷下,单位面积径向压力随层数的增加而逐渐减小,内层径向压力最大;锥度收卷下,单位面积径向压力随锥度系数增大而减小,可适当减少缝头印的影响层数;幂函数收卷下,单位面积径向压力随着指数的减小而大幅度减小,可以有效预防缝头印的产生,提高针织物的染色质量。 3)对比3种收卷方式,幂函数收卷得到的剩余缠绕张力分布最均匀,且内层的剩余张力最大,可避免发生折皱,获得较好的布卷卷形;且幂函数收卷得到的单位面积径向压力值最小,有利于预防缝头印的出现,获得高质量的染色织物。 FZXB [1] 赵北琳.活性染料冷轧堆染色工艺与色条疵病的研究[D].上海:东华大学,2007:1-11. ZHAO Beilin. The research of cold pad-batch dyeing technics and shade bar with reactive dyes[D]. Shanghai: Donghua University, 2007:1-11. [2] 李鹏飞.改善活性染料冷轧堆染色缝头色条的研究[D]. 上海:东华大学,2008:1-30. LI Pengfei. Study on improvment of the shade stripe in cold pad-batch dyeing with reactive dyes [D]. Shanghai: Donghua University, 2007:1-30. [3] 朱月琴.纯棉针织物冷轧堆染色小样仿色的改进[J]. 印染,2014(4):22-24. ZHU Yueqin. Improvement of cold pad-batch sampling of cotton knits[J]. China Dyeing & Finishing, 2014(4):22-24. [4] 杨娅君,郭乙木.纺织物带材收卷后的应力分布[J]. 纺织学报,2003, 24(6):56-58. YANG Yajun, GUO Yimu. The stress distribution after the textile band rolled[J]. Journal of Textile Research, 2003, 24(6): 56-58. [5] 林佳辉.基于变质量系统的卷绕内张力变化规律研究[D].杭州:浙江理工大学,2013:1-30. LIN Jiahui. The research of winding tension variation law based on variable mass system[D]. Hangzhou: Zhejiang Sci-Tech University, 2013:1-30. [6] 刘成旭,邢静忠,陈利,等.柔性厚壁筒环向缠绕张力分析与设计[J].固体火箭技术,2013, 36(2):261-265. LIU Chengxu, XING Jingzhong, CHEN Li, et al. Analysis of residual winding tension and design of winding tension for hoop winding on flexible cylinder[J]. Journal of Solid Rocket Technology, 2013, 36(2):261-265. [7] 杨桂通.弹性力学[M].2版.北京:高等教育出版社,2004:85-87. YANG Guitong. Elastic Mechanics[M]. 2nd ed. Beijing: Higher Education Press, 2004:85-87. [8] MOLLAMAHMUTOGLU C, GOOD J K. Modeling the influence of web thickness and length imperfections resulting from manufacturing processes on wound roll stresses[J]. Cirp Journal of Manufacturing Science & Technology, 2014:22-33. [9] 吴德会,谭珍祥,杨华群.玻璃布包装中锥度收卷的内张力分布及其参数确定[J].包装工程,2005, 26(6):8-11. WU Dehui, TAN Zhenxiang, YANG Huaqun. Taper rolling-up and param eter determ ination in glass fabric packaging[J]. Packaging Engineering, 2005, 26(6):8-11. [10] 李翠玉.针织物的细观本构模型和织物的屈曲分析[D].天津:天津大学,2005:84-90. LI Cuiyu. The micro-constitutive model of knitted fabric and buckling analysis of fabric[D]. Tianjin: Tianjin University, 2005:84-90. [11] 陈立秋.印染厂节能减排实用工艺装备技术: 十八: 染整工艺张力控制[J]. 印染,2012,38(5): 46-49. CHEN Liqiu. Processes and equipments for energy saving and emission reduction in dyeing plants: XVIII: tension control in dyeing and finishing pro-cess[J]. China Dyeing & Finishing, 2012,38(5):46-49. [12] 邢静忠,梁清波,刘成旭,等. 圆柱形厚壁缠绕件的环向缠绕张力分析的逐层叠加法[J]. 固体火箭技术, 2015(2):261-266. XING Jingzhong, LIANG Qingbo, LIU Chengxu, et al. Analysis of winding tension for hoop winding on deformable thick-walled cylinder with superposition by layers[J]. Journal of Solid Rocket Technology, 2015(2):261-266. Knitted fabric winding tension of cold pad batch dyeing YIN Miaomiao1, YUE Xiaoli1, ZHONG Yi2, CHEN Huimin1 (1. College of Mechanical Engineering, Donghua University, Shanghai 201620, China; 2. Key Laboratory of Eco-Textile, Ministry of Education, Donghua University, Shanghai 201620, China) In order to solve the problem of dyeing color difference due to seam allowance during cold pad batch dyeing, focused on knitted fabric, the paper analyzed the reasons for the formation of seam allowance imprint, used the theory of thick wall tube and iteration law to analyze the force of knitted fabric in the process of winding, and established a mathematical model for the winding of knitting fabric. The paper analyzed the values of residual tension and radial pressure under constant winding tension and taper winding tension, and established the model under power function winding tension taking the control of seam allowance imprint as the goal and accounting for the roll shape of knitted fabric. It is concluded that the radial pressure under power function winding is much smaller than the constant tension and taper winding, and the smaller exponent of the power function, the more uniform distribution of the residual tension, the smaller radial pressure, which is conductive to the control of seam allowance imprint to obtain high quality dyed fabric, providing the reference in the design of winding tension for cold pad batch dyeing of knitted fabric. seam allowance imprint; winding tension; cold pad batch dyeing; knitted fabric 10.13475/j.fzxb.20160504607 2016-05-20 2016-12-30 印染清洁生产关键技术研究及示范项目(2014BAC13B02) 尹苗苗(1993—),女,硕士生。主要研究方向为机械设计、纺织生产在线测控。陈慧敏,通信作者,E-mail: ch_huimin@dhu.edu.cn。 TS 181 A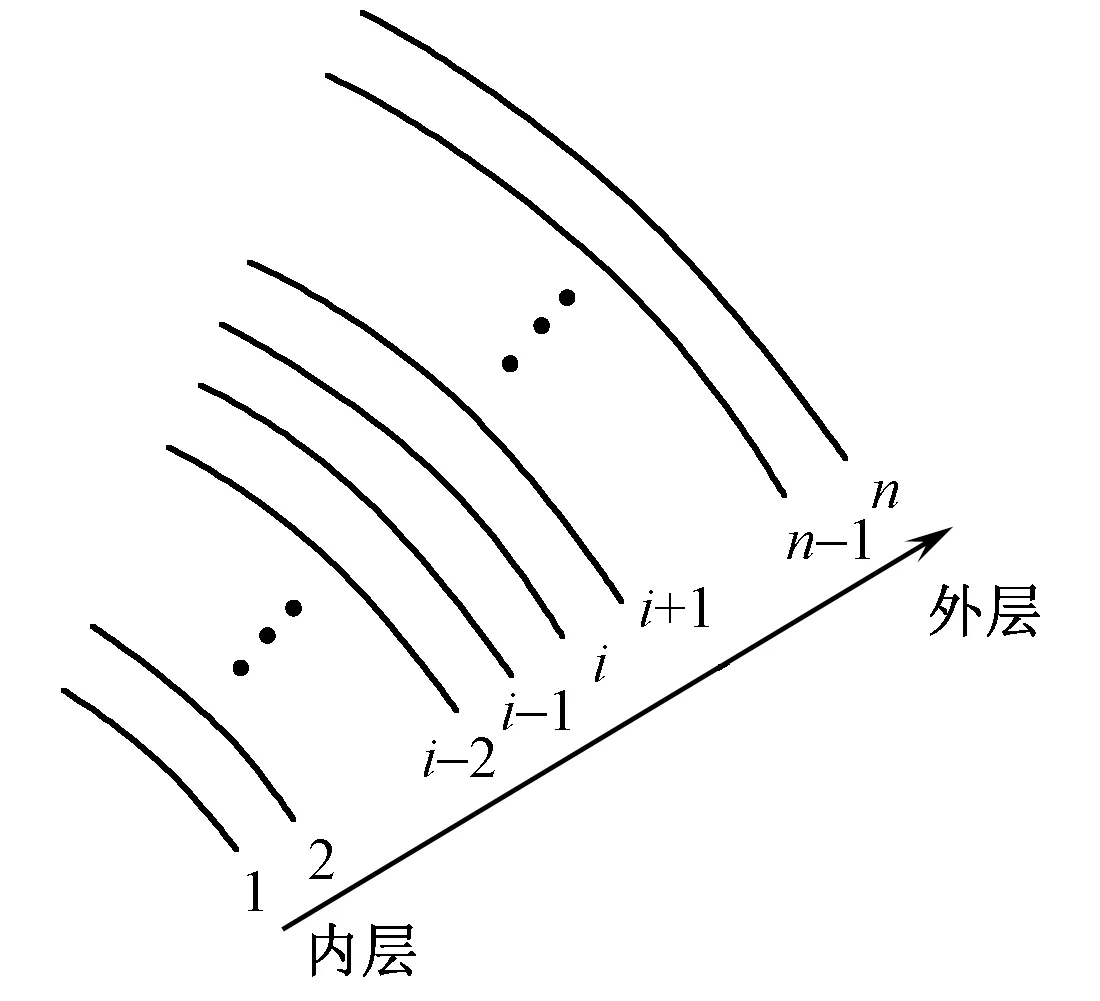

4 不同收卷方式下数值计算



5 结 论

