MPPSK-OFDM复合调制系统的解调性能分析
陈志敏, 李靖超
(上海电机学院 电子信息学院, 上海 201306)
MPPSK-OFDM复合调制系统的解调性能分析
陈志敏, 李靖超
(上海电机学院 电子信息学院, 上海 201306)
多元位置相移键控与正交频分复用技术(MPPSK-OFDM)组成的复合调制系统,其接收端采用OFDM解调方式进行混合信号的接收,对于MPPSK信号来说,这种解调方式势必会带来一定的干扰。首先给出复合调制系统的结构及解调方案,然后从MPPSK-OFDM复合调制信号的时域结构出发,逐步推理,最终得出即使在无噪声信道中,接收端解调出的也是一个对发端星座点的有偏估计,且接收信号呈现以发端星座点为均值,方差随K∶N呈正比的高斯分布的结论。
多元位置相移键控; 正交频分复用技术; 复合调制; 干扰分析
我国调幅(Amplitude Modulation,AM)广播采用保留载波的双边带调幅(DSB-AM)体制,其调制信号由一个不携带信息的正弦波和上下边带对称的模拟边带组成[1]。正弦载波仅仅是为了保证收音机的包络检波效果,它不携带信息却占用了大量功率,若采用具有类载波性质的超窄带(Ultra Narrow Band,UNB)调制波形替代正弦载波,则可望充分利用载波功率,并实现模拟信号与数字信号的同传[2-6]。参考带内同频道(In Band on Channel, IBOC)标准,只要数字调制信息的功率谱边带在模拟主信号带宽内低于载波50 dB,即可忽略数字信号对模拟信号的干扰,实现模数同传。因此,基于多元位置相移键控(M-ary Position Phase Shift Keying, MPPSK)与正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术的复合调制方案不会影响现有AM收音机对模拟音频的接收,该复合调制既可作为一个过渡方案,又可通过对模拟音频边带的进一步处理实现对广播系统载波、边带全数字化改造。目前,该复合系统直接采用OFDM的解调方式进行复合信号的接收,但是,对于复合信号中的MPPSK信号来说,这种解调方式势必会带来一定的干扰,而对此干扰的研究工作尚未展开。基于此,本文从复合调制系统的结构及解调方案出发,通过研究MPPSK-OFDM复合调制信号的时域结构,实现对复合调制系统解调误差的分析并给出相应的结论。
1 MPPSK-OFDM复合调制系统结构
1.1 发射机结构
相对AM广播而言,复合调制发射机仅仅是将原有的正弦载波替换成了UNB调制后的准载波,如图1所示。对MPPSK系统而言,它是一个相位调制系统,其载波的相位、幅度均被调制;相位信息被数字信号调制,幅度信息被AM广播的模拟音频或OFDM基带调制。

图1 复合调制发射机结构示意图
图1中的上变频模块用虚框表示,由于其大部分广播发射机采用射频发射体制,信号在发射频段上调制;其他发射机则采用465 kHz中频调制,再通过上变频后发射。从MPPSK调制的角度考虑,直接射频调制方式会给MPPSK的参数选取带来很大灵活性,频谱性能也更佳。而对于载波的选择,采用MPPSK调制信号可在不降低解调性能的情况下,增加码率,降低线谱功率,故现阶段针对基于复合调制的数字化广播硬件实现方案中采用MPPSK作为载波。
1.2 接收机结构
如图2所示,复合调制系统的发射机将MPPSK调制信号与模拟音频/编码OFDM(COFDM)基带信号复合调制后发射。由于发射信号有2路信息,接收机就需要将复合信号分为两路进行解调;① 模拟音频/COFDM基带的接收与解调;② MPPSK信号的接收与解调。

图2 复合调制接收机结构示意图
2 复合调制系统的解调
2.1 AM边带解调系统
第1路解调负责提取复合调制信号的包络。若采取模拟音频+数字载波的复合调制方式,则该包络即为模拟音频;若采取模拟COFDM的音频基带调制方式,则该包络为COFDM基带信号,还需要另加一个COFDM解调器进行解调。对于OFDM的解调,基于相干解调获取基带这一前提,而复合调制系统对OFDM基带的提取是基于AM包络检波。包络检波作为一种结构简单的非相干解调方式,与相干解调的区别主要表现为两方面:
(1) 解调性能相异。在大信噪比情况下,AM信号包络检波器的性能与相干解调器相同。但随着输入信噪比的减小,包络检波器将会出现门限效应,使解调器的输出信噪比急剧恶化。
(2) 包络检波输出不易受频偏影响。包络检波的功能可仅通过取绝对值加低通滤波来实现。实质是提取幅度调制信号的包络,而小范围的频偏并不改变调制信号的包络,故其解调输出不会受频偏影响。图3为在频偏1 Hz、相偏π/3情况下包络检波与相干解调提取的信号星座图。由图可见,载波偏差对包络检波的输出影响不大,故其载波同步的步骤可以忽略;而相干解调则需要估计并补偿载波的偏移。

(a) 包络检波

(b) 相干解调
2.2 AM载波解调系统
第2路解调负责对作为DSB-AM系统数字载波的MPPSK调制信号的解调。MPPSK解调器主要包含如下功能模块:
(1) 限幅。由于数字载波MPPSK被模拟音频所调制,其包络会发生起伏变化(见图4(a))。这种起伏会带来冲击滤波响应幅度的变化,影响判决门限的选取。限幅操作将零以下的幅值设为-1,零以上的幅值设为1,对携带信息的相位影响不大,却能保证滤波信号冲击幅度的峰值恒定,如图4(b)所示。
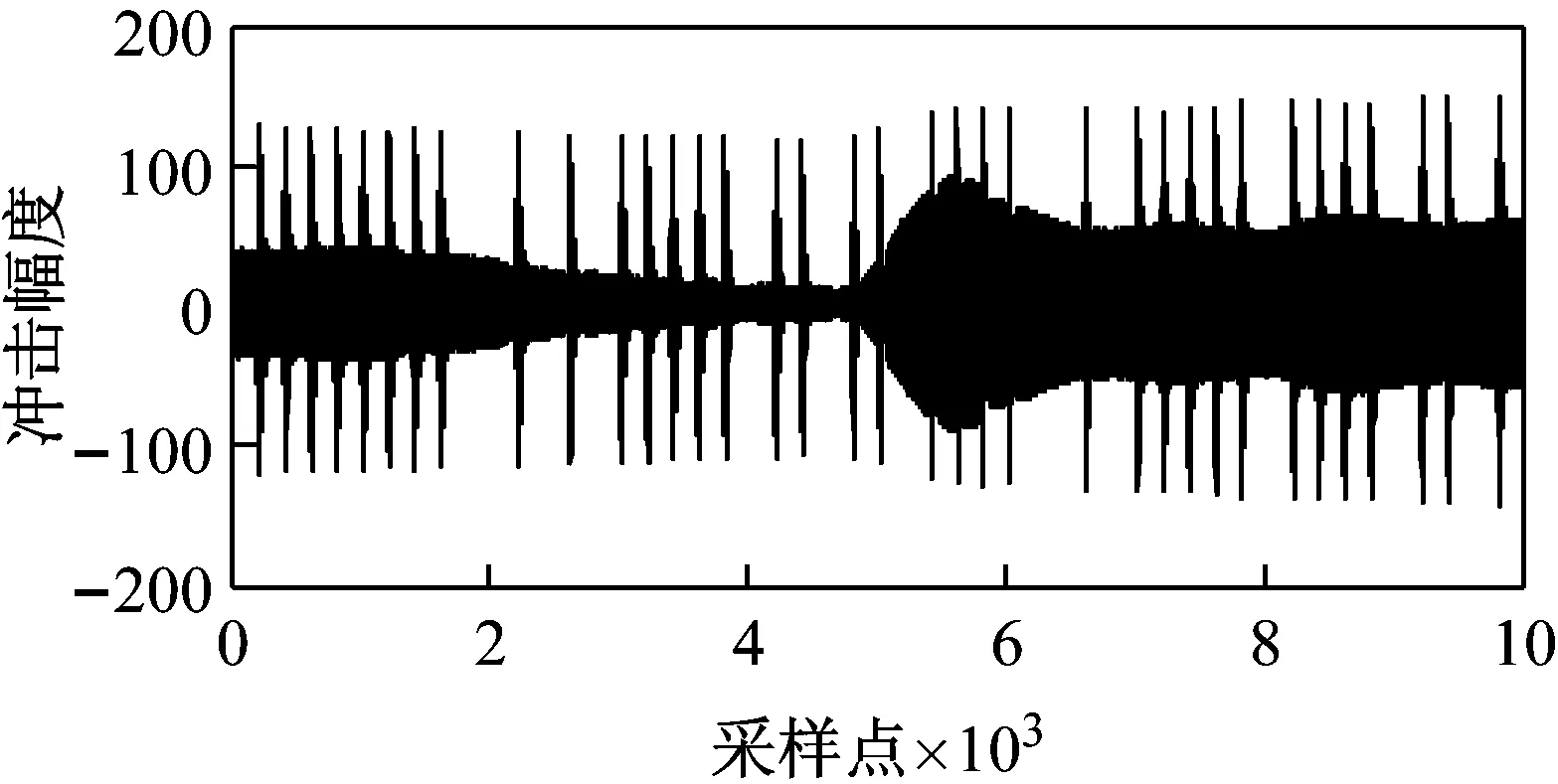
(a) 未限幅信号经过冲击滤波器的输出
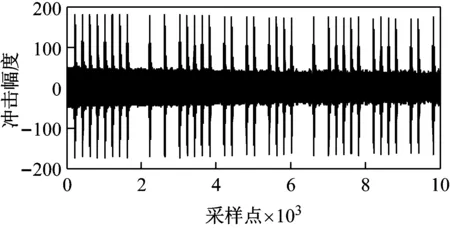
(b) 已限幅信号经过冲击滤波器的输出
(2) 冲击滤波器。一种有极窄陷波-选频特性的IIR滤波器,是MPPSK解调的关键模块[7-10]。
(3) 位同步模块。该模块充分利用了冲击包络与归零码的相对位置关系,不用锁相环也能较好地实现位同步,其结构如图5所示[11-12]。其原理如下:将预处理模块输出的冲击包络送入可变延时器,将归零码同时送入时延计算器和时钟发生器,当出现归零码“1”时,时延计算器测量其高电平持续时间,根据冲击包络最高处与归零码“1”下降沿的相对位置关系,得到冲击包络的延时长度;在归零码“1”的下降沿重置时钟发生器,实现位同步时钟的调整;同时,可变延时器根据时延计算器计算出的延时长度对冲击包络进行延时,从而在一个码元内实现快速、准确的位同步。时延计算器本质上是一个计数器,用于计算归零码高电平的持续时间;而可变延时器本质上是一个可寻址的移位寄存器,其寻址地址就是冲击包络的延时长度;控制模块用于控制时钟发生器的输出频率,以适应不同码率下的同步要求。

图5 位同步结构框图
(4) 积分判决模块。码元判决模块可以使用常规的积分判决,即在位同步时钟的指导下,对延时后的包络进行积分,然后与合适的判决门限进行比较,即可实现判决。事实上,如果充分利用冲击包络的特征进行判决效果会更好。当出现冲击包络时,表明当前码元为“1”;没有冲击包络,则码元为“0”。因此,可以采用码元内积分判决的方式进行判决。在位同步时钟上升沿取一定数量的采样点进行积分,在位同步时钟的下降沿也取等量的采样点进行积分,将两次积分结果的差值与判决门限相比较,从而实现码元判决。这种码元内积分判决的方法充分利用了冲击包络的特点,提高了判决时的信噪比,具有良好的判决效果。
3 解调方式的误差分析
上述MPPSK-OFDM复合调制的系统仿真已经证明方案可行[13-16],然而,MPPSK作为准正弦信号,而接收端按OFDM解调方法处理接收信号必然会带来一定干扰。本文从MPPSK-OFDM信号的时域结构出发,对解调误差进行分析。
假设载波频率为ωc,XR(t)、XI(t)分别为频域共轭对称、反对称部分对应的时域,则OFDM频带信号为XR(t)cos(ωct)+XI(t)sin(ωct)。
为推导方便,设MPPSK的伪基带信号为B(t),则接收端信号为
y(t)=B(t)· [XR(t)cos(ωct)+XI(t)sin(ωc(t)]
(1)
按一般方式解调OFDM信号,即式(1)等号右边乘以cos(ωct)得到:
y′(t)=0.5B(t)XR(t)+0.5B(t)· [XR(t)cos(2ωct)+XI(t)sin(2ωct)]
(2)
若B(t)=1,则低通滤波后可得XR(t),即普通OFDM频谱搬移,N∶K很大(其中,N为MPPSK调制一个码元周期内的载波个数,K为N个载波内的跳变载波数),载频够高时,MPPSK基带近似为1,连续谱分量仅由低功率跳变区域产生,且均匀分散于极宽频段内,故此处近似接收端,可以通过低通无损获得0.5B(t)XR(t)部分。
假设OFDM频域共L根调制谱,ωi为OFDM基带的第i根载频频率,Tc为OFDM码元周期,实数ai、bi携带信源信息,则复合调制基带时域实部信号为
(3)
接收端分离出B(t)XR(t)后,为提取系数am,1≤m≤L,将式(3)等号两边同时乘以cos(ωmt),得到
B(t)XR(t)cos(ωmt)=
bisin(ωit)cos(ωmt)],t∈[0,Tc]
(4)
将式(4)在Tc内积分,可得到
(5)

设B(t)=1-Bδ(t),Bδ(t)为接近采样函数的窄脉冲,幅度为2,宽度为K/fc,K为MPPSK中跳变载波数,fc为载频。
当OFDM周期数>>MPPSK码元周期数,信源0、1码元等概时,有用项为
0.5am[(N-K)/N]Tc
(6)
剩余项为
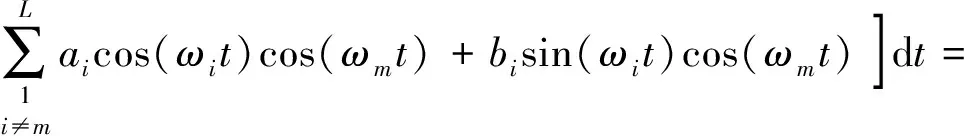
(7)
由正交性,对式(7)进行整理,得
式(7)=
(8)
由于采样函数Bδ(t)为随机过程,直接对式(8)进行积分是不现实的,故需要用间接方法求其近似值。当OFDM信号具有足够宽的基带带宽时,每个Bδ(t)获得的“采样值”将近似互相独立。根据中心极限定理,独立、同分布随机变量大量叠加将接近高斯随机变量。由于MPPSK信号跳变位置的随机性,Bδ(t)可能在时域任意处经过正弦函数“衰减”后,对均匀分布的幅度随机变量ai进行采样,最终叠加生成某个高斯随机变量。由于各求和项均值为0,故该和的随机变量均值为0,关键在于确定该随机变量的方差,因为其决定着使用一般算法解调OFDM的可靠程度。
注意到
(9)
即式(8)中的干扰项为Bδ(t)对XR(t)cos(ωmt)的采样值之和。
假设OFDM一个码元周期Tc的符号能量平均为E0,包括了实部和虚部两部分能量,且虚、实两部分通常能量相等。运用帕斯瓦尔定理可知,时域采样x和频域向量X存在如下关系:
Ax=X
A为系数矩阵,则
xHAHAx=xHx
即时、频功率相等,故可根据其载波的星座图计算出E0。
假设OFDM带宽足够宽,Bδ(t)采样值相关性很弱,故可以全概率公式进行求和近似。设f(x)为cos(X)的概率密度函数,X为[0,2π]内均匀分布的随机变量,|x|表示对采样值的幅度增益,有
(10)

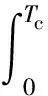
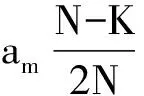
4 解调性能仿真
图6所示为复合调制下的MPPSK解调性能图,采样率为10倍,在未添加中频滤波的情况下,信噪比为6 dB时,可达到10-4的误码率。现有模拟AM广播收音机存在中频滤波器,该滤波器虽然滤去了模拟音频的带外噪声,却对数字载波的信息造成了一定损伤。图6同时给出了经过中频端滤波后,复合调制信号中MPPSK的解调性能(调制参数如下:M=256,N=510,K=2,相位偏差θ=π/3),所添加中频滤波器的3 dB带宽约为80 kHz。由图6可见,添加中频滤波器比未添加中频滤波器的MPPSK解调性能约差3 dB。这一性能损失看似可惜,但是作为兼容旧体制的代价,3 dB的损失仍在可以接受的范围之内。

图6 复合调制MPPSK误码率曲线
5 结 语
复合调制方案最根本的好处就是将数字载波引入系统之中,故数字载波的解调误码率性能在复合调制方案中至关重要。数字载波归根到底也是一种调制方式,跳变的时间和相位越小,就越接近正弦载波,其误码率性能也越差。本文通过对复合调制解调误差的分析,可以有效地量化现有复合调制系统的性能,针对现有调制方式的弊端,寻求更合理的解调方案,对于复合调制系统性能的改进以及我国广播系统的全面数字化具有一定的实际意义。
[1] 电子工业部第762厂. GB/T 9376—1988 中波和短波调幅广播发射机基本参数[S].北京:中国标准出版社, 1988.
[2] WALKER H R. High speed binary data communication system: US 4742532[P/OL]. 1988-05-03 [2016-07-25]. http://www.freepatentsonline.com/4742532.html.
[3] WALKER H R. VPSK and VMSK modulation transmit digital audio and video at 15 bits/sec/Hz[J]. IEEE Transactions on Broadcasting, 1997, 43(1): 96-103.
[4] 吴乐南. 超窄带高速通信进展 [J]. 自然科学进展, 2007, 17(11): 1467-1473.
[5] 冯熳.高效调制的关键问题研究 [D]. 南京:东南大学,2008: 35-40.
[6] HE Feng, WU Lenan. Analysis of power spectrum of continuous phase waveforms for binary modulation communications[C]∥International Conference on Ultra Modern Telecommunications & Workshops. Piscataway, NJ: IEEE, 2009:1-5.
[7] 吴乐南,靳一,冯熳等. 多元位置随机极性MCP-EBPSK调制和解调方法:CN201110431039.5[P].2012-07-04[2016-08-06].http:∥patentool.wanfangdata.com.cn/Patent/Details?id=CN201110431039.5.
[8] 陈贤卿,吴乐南. EBPSK解调器中利用SVM概率输出的LDPC译码[J].信号处理, 2011, 27(9):1286-1290.
[9] 冯熳, 高鹏, 吴乐南. 超窄带调制信号的特殊滤波分析与仿真[J]. 东南大学学报(自然科学版), 2010,40(2):227-230.
[10] 吴乐南, 但吉兵. 扩展的二元相移键控调制突发通信快速同步方法: CN201010228690.8[P]. 2010-11-24[2016-08-06].http://d.wanfangdata.com.cn/Patent/CN201010228690.8/.
[11] CHEN Zhimin, WU Lenan,CHEN Peng.Efficient modulation and demodulation methods for multi-carrier communication[J].IET Communications,2016, 10(5): 567-576.
[12] Van WATERSCHOOT T,MOONEN M. A pole-zero placement technique for designing second-order IIR parametric equalizer filters[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007,15(8): 2561-2565.
[13] CHEN Peng, WU Lenan.Waveform design for multiple extended targets in temporally correlated cognitive radar system [J]. IET Radar, Sonar & Navigation, 2016, 10(2): 398-410.
[14] WANG Wei, WU Lenan, ZHU Bingcheng. An AM-compatible hybrid modulation for broadcasting[C]∥2012 7th International ICST Conference on Communications and Networking in China (CHINACOM).Kunming, China: IEEE,2012: 197-201.
[15] 余静,吴乐南,靳一. 基于量子粒子群优化的数字冲击滤波器自动设计[J]. 东南大学学报(自然科学版),2012, 42(2), 224-228.
[16] ZHU Bingcheng, YANG Fan, CHENG Julian, et al.Performance bounds for diversity receptions over arbitrarily correlated Nakagami-m fading channels[J].IEEE Transactions on Wireless Communications, 2016, 15(1): 699-713.
Demodulation Performance of Hybrid MPPSK-OFDM System
CHENZhimin,LIJingchao
(School of Electronic Information, Shanghai Dianji University, Shanghai 201306, China)
Since a hybrid m-ary position phase shift keying (MPPSK) system uses orthogonal frequency division multiplexing (OFDM) to demodulate hybrid signals, interference to the MPPSK signal may occur. We first propose a hybrid system structure, which combine the MPPSK and OFDM. Then, we analyze the time-domain expression of the hybrid signal and give the conclusion that even in a noise-free environment, the demodulated signal is a biased estimate of the transmitted signal. The mean of the
signal is located at a biased point in the constellation and the distance obeys Gaussian distribution with a variance proportional toK/N.
m-ary position phase shift keying (MPPSK); orthogonal frequency division multiplexing (OFDM); hybrid modulation; error analysis
2017 -03 -09
国家自然科学基金项目资助(61601281,61603239)
陈志敏(1985-),女,讲师,博士,主要研究方向为通信中的信号处理,E-mail: chenzm@sdju.edu.cn
2095 - 0020(2017)02 -0063 - 06
TN 911.3
A

