鹰式波浪能发电装置水动力学性能分析及优化

张亚群，游亚戈，盛松伟，王文胜

（中国科学院 a.广州能源研究所；b.可再生能源重点实验室，广州 510640）

鹰式波浪能发电装置水动力学性能分析及优化

张亚群a，b，游亚戈a，b，盛松伟a，b，王文胜a，b

（中国科学院 a.广州能源研究所；b.可再生能源重点实验室，广州 510640）

根据牛顿第二定律，对鹰式波浪能装置多个浮体进行了力学分析，基于微波理论，通过每个浮体之间三种模态的运动耦合，建立了流体力、阻尼力、铰接力、静水回复力等内外力之间的力学方程组。通过以运动浮体为边界条件求解多个浮体的水动力学参数，代入方程组中计算求得最优外加阻尼和最优俘获宽度比，从而优化设计方案，得到此时各浮体在纵荡、垂荡和纵摇三种运动模态下的位移幅值，以及阻尼力、铰接力、液压缸运动速度等相关参数。研究成果为鹰式波浪能装置的设计及制造提供了理论参考和依据。

鹰式波浪能发电装置；水动力学；俘获宽度比；最优外加阻尼；优化设计

0 引 言

海洋波浪能作为一种绿色可再生能源，备受人们重视。现今，开发利用海洋波浪能发电的装置发展迅速，其在外形结构上具有多样性，大致划分为以下几种：振荡水柱式、越浪式、软囊式和振荡浮子式。其中振荡浮子式波浪能装置类型多、发展快，如点吸收式、鸭式、筏式、摆式和鹰式等[1-2]。

鹰式波浪能装置（Sharp Eagle）属于一种新型漂浮式振荡浮子式波浪能装置。目前，关于鹰式波浪能装置的研究文献较少。文献[3-4]是关于鹰式WEC研究工作的全面介绍，文献[5]介绍了模型试验方面的研究，文献[6]是关于波能装置状态信息采集和控制的技术方案方面的研究，文献[7-8]是关于装置的限位梁撞击破坏的损伤机理研究，其中文献[2]对鹰式WEC的水动力学性能进行了初步分析。

本文以鹰式Ⅱ号波浪能发电装置为实例，通过分析各浮体在三个模态下的运动耦合[9]，建立单个浮体的力学模型，并列出各个作用力的数学方程；通过数值模拟得到水动力学参数，求解力学模型，逐步对鹰式波浪能装置参数设计进行优化，最终获得最优设计方案。

1 力学模型

鹰式Ⅱ号波浪能装置的基本结构如图1所示，由鹰头吸波浮体（浮体1）、水下附体（浮体2）、能量转换系统和锚泊系统组成。鹰头吸波浮体通过C点的门型铰链安装在水下附体上。能量转换系统中的液压缸的有杆端安装于鹰头吸波浮体A点上，无杆端安装于水下附体B点上。鹰头吸波浮体的重心位于点1，水下附体的重心位于点2。

图1 鹰式波浪能装置结构简图Fig.1 Structure chart of Sharp Eagle WEC

假设作用在浮体k（鹰头吸波体或水下附体，k=1或者k=2）上所受的合力为，由流体力、阻尼力、静水回复力、铰接力、静水压力和重力组成。但静水压力的合力（即静浮力）与重力平衡，故忽略不计。鹰式波浪能发电装置在波浪中的运动有六个运动模态，为纵荡、横荡、垂荡、横摇、纵摇和艏摇（分别由j=1，2…，6表示）。其中纵荡、垂荡、纵摇三种运动模态对波浪能装置吸收波浪能运动影响最为显著。因此在对鹰头吸波浮体与水下附体进行水动力学运动分析时，其它方向的运动模态暂不考虑。

假设浮体k的质量为m（k），根据牛顿第二定律，在j运动模态下有

除去时间因子，将Fj（t）分解后，得：

1.1 流体力

作用在鹰式波浪能装置浮体k上的流体力可分解为：

根据伯努利方程，浮体k上受到的j运动模态方向的波浪激励力可表示为

辐射力可以表示为：

式中：ρ为计算域流体密度；ω为波浪圆频率；S为湿表面；nj为浮体k湿表面的法线在j运动模态方向的投影；为k浮体i模态的运动在j运动模态方向引起的附加质量，为k浮体i模态的运动在j运动模态方向引起的阻尼系数。

1.2 阻尼力

其中，vA在A、B连线的投影可表达为：

类推，则B点的速度表示如下：

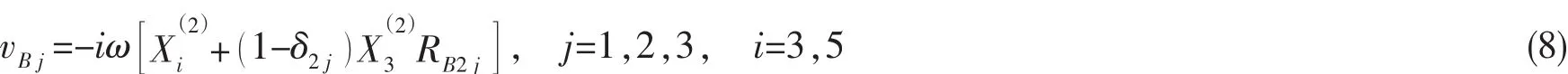
如图1所示，鹰头吸波浮体与水下附体为两个独立的浮体，两者之间通过门铰连接。无论在静水中，还是运动过程中，两者均受到铰接力FJ的约束作用，作用点在C点。由于C点不仅位于鹰头吸波浮体上，同时也位于水下附体上。则C点的速度可以同时表示为：

考虑鹰头吸波浮体与水下附体只在j=1，3运动模态受铰接力作用，Vj=-iωXj，则：

1.4 静水回复力

式中：A为水线面面积，当物体完全淹没时，A=0。

1.5 最优外加阻尼计算

在不列颠哥伦比亚省的海岸上，哈蒙德和摩尔回忆起20世纪90年代末的漂流木打捞盛景，尽管如今打捞到的漂流木越来越少，收入也相当微薄，但摩尔说只要他能坚持下去，他就会一直在海边和漂流木打交道。哈蒙德和摩尔他们会是这片海岸上最后的海滩拾荒者吗？他耸了耸肩，指着屋子前的一处打捞来绑成筏子的半打漂流木说道，这些都是他7岁的儿子从海上拖拽来的。

鹰式波浪能装置能量转换系统为液压式，由液压缸提供阻尼力，有效做功为克服阻尼力运动过程所做的功。阻尼力的大小，不仅影响了能量转换系统的转换效率，而且影响了鹰头吸波浮体俘获波浪能的功率。

一个入射波周期里，波浪能装置克服阻尼力所做的功及得到的平均功率为：

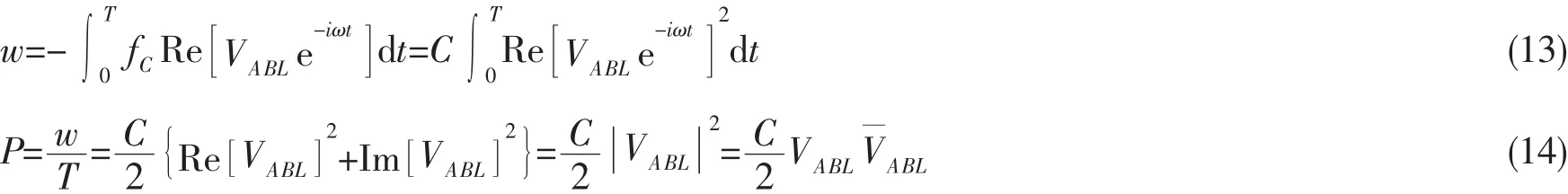
当平均功率取得最大值时，阻尼力定义为最优外加阻尼，得：

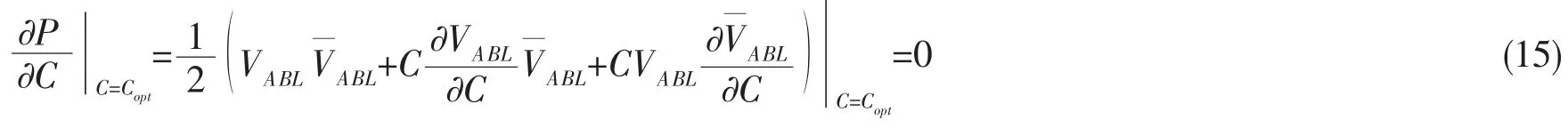
式中：VABL与共轭；Copt为最优外加阻尼。

1.6 俘获宽度比计算

俘获宽度比定义为：单位宽度的波浪能装置俘获波浪能的功率与单位宽度的来波功率的比值。通常用俘获宽度比的大小来衡量一个波浪能装置俘获波浪能的能力的强弱，同时也为优化波浪能装置的设计的标准。

波浪能装置对应的来波功率为：

由（15）式可知，波浪能装置在最优外加阻尼力下的俘获宽度比为：

式中：η为波浪能装置最优阻尼下的俘获宽度比；P0为波浪能装置迎波宽度内入射波功率；g为重力加速度；H为入射波浪波高；k为波数；B为波浪能装置的迎波宽度；Popt为波浪能装置在最优外加阻尼下俘获的波浪能功率。

2 数值模拟

基于上述力学分析的基础上，进行鹰式波浪能装置的水动力学数值模拟。按照鹰式波浪能装置预定投放海域的海况为数值模拟的试验环境，入射波为线性规则波，周期范围为1-16 s，波幅为1 m，方向与鹰式波浪能装置之间角度为0°。

2.1 波浪力分析

在单位波幅作用下，鹰头吸波浮体及水下附体三种运动模态下受到的波浪激励力及力矩，如图2（a）～（c）数据曲线所示，前者受到的波浪激励力或力矩均比后者受到的小。

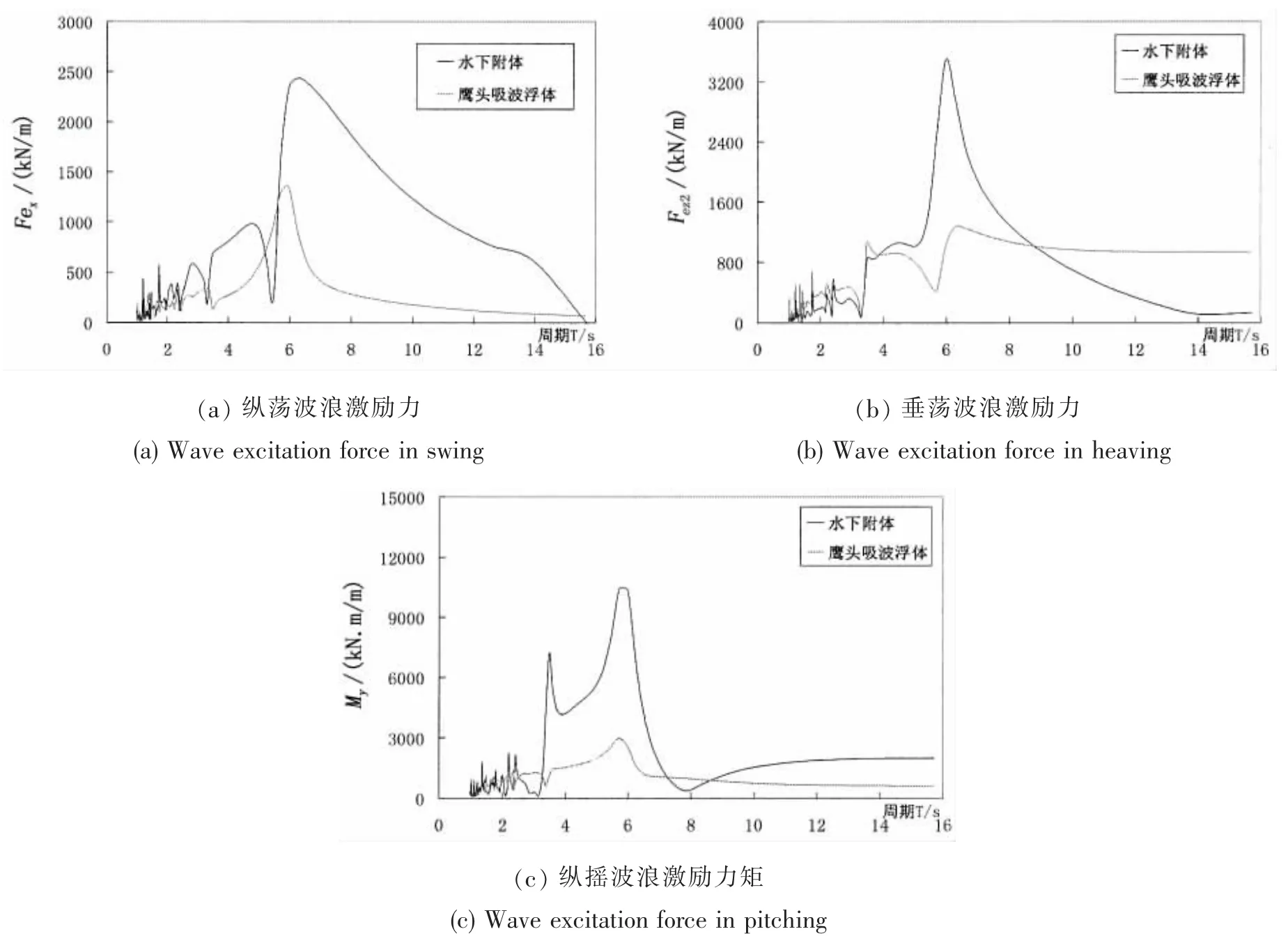
图2 各运动模态的力、力矩Fig.2 Force and torque in different motion modes

2.2 附加质量

图3、图4分别为鹰头吸波浮体和水下附体在三种模态下运动产生的附加质量。从图中可观察到，三种运动模态下鹰头吸波浮体的附加质量均小于水下附体的附加质量。另外鹰头吸波浮体的纵摇运动、纵荡运动附加质量小，然而水下附体在这两个模态下运动的附加质量大。一般情况下，附加质量的数值大小主要是由鹰头吸波浮体和水下附体做不同运动时，提供的阻碍水质点运动的面积决定的。因此，在波浪能装置设计中，某个模态下附加质量越大，说明装置在此模态下的运动惯性越大，产生运动所需的动力越大。

图3 鹰头吸波浮体的附加质量Fig.3 Added mass of the Eagle head buoy

图4 水下附体的附加质量Fig.4 Added mass of the underwater appendage

2.3 阻尼系数

图5、图6分别为鹰头吸波浮体和水下附体在三种模态下运动产生的阻尼系数。三种模态运动下，前者产生的阻尼系数大小排序与后者相同，但数值上前者均远远小于后者。在波浪能装置设计中，阻尼系数通常表明了装置在做俘获波浪能的运动中遇到的阻力。某种模态下阻尼系数越小，则波浪能装置在做该模态运动时遇到的阻力越小；反之，当某种模态下阻尼系数越大，则波浪能装置在做该模态运动时遇到的阻力越大。例如，图2-9中，纵摇运动模态下，鹰头吸波浮体的阻尼系数小于水下附体的阻尼系数，则鹰头吸波浮体遇到的阻力远比水下附体小。如果两者之间的阻尼系数差值越大，那么两者纵摇运动幅度差距越大，更利于波浪能装置俘获波浪能。

图5 鹰头吸波浮体的阻尼系数Fig.5 Damping coefficient of the Eagle head buoy

图6 水下附体的阻尼系数Fig.6 Damping coefficient of the underwater appendage

3 优化设计

液压缸以阻尼力做功的形式将吸收的波浪能转换为液压能。阻尼力是决定俘获宽度比的重点，而外加阻尼是确定阻尼力的关键。通过最优外加阻尼可得到最优阻尼力，从而获得最佳俘获宽度比值，保证鹰式波浪能装置能够持续地吸收波浪能并高效地转换为液压能。

假设外加阻尼C=100 000～800 000 Ns/m，根据上述数值模拟结果以及（15）～（17）式，计算各周期下对应的俘获宽度比曲线如图7所示。从图7中计算得最优外加阻尼为Copt=300 000 Ns/m，此时最优俘获宽度比曲线如图8所示。

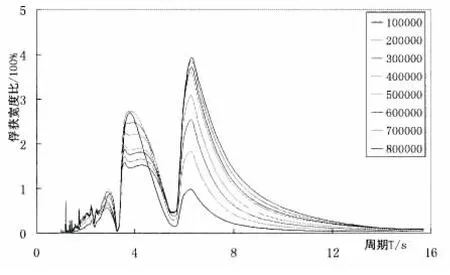
图7 不同外加阻尼对应的俘获宽度比Fig.7 Capture width ratio of different outer damping

图8 最优俘获宽度比Fig.8 Optimal capture width ratio

根据最优外加阻尼Copt=300 000 Ns/m，计算装置在单位幅值入射波作用下纵荡、垂荡和纵摇三种模态的运动幅值、液压缸提供的阻尼力、液压缸丝杠的运动速度、液压缸与装置铰接点上的铰接力（纵荡方向及垂荡方向），如图9-14所示。

从图9～11观察得到，同种模态下，水下浮体的运动幅度均小于鹰头吸波浮体的运动幅度。对于鹰头吸波浮体，随着周期增大，运动幅值不断增大。对于水下附体，无论哪种运动模态下，运动幅值达到最大值后慢慢减小。在单位幅值的入射波作用下，垂荡运动模态下的最大运动位移幅值约为纵荡运动模态下的2倍，纵摇运动模态的最大运动角度幅值为20.92°。

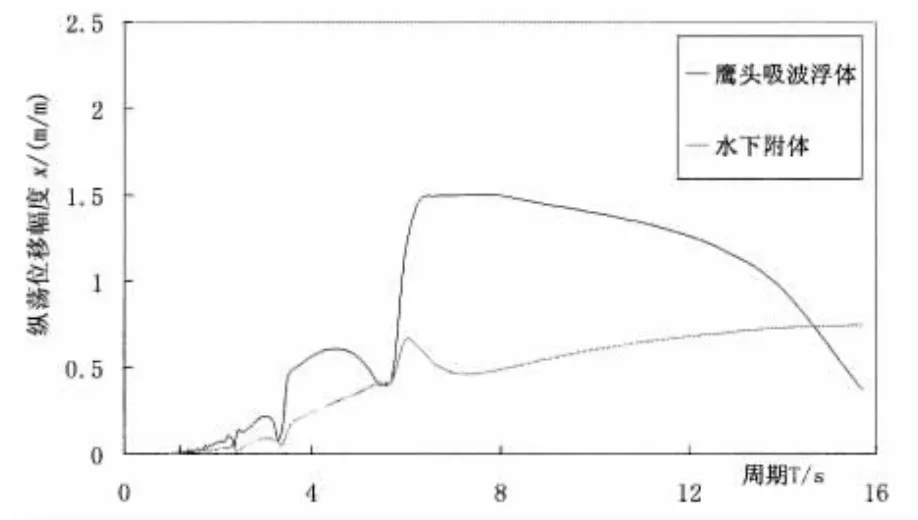
图9 纵荡运动的位移幅值Fig.9 Displacement amplitude in swing

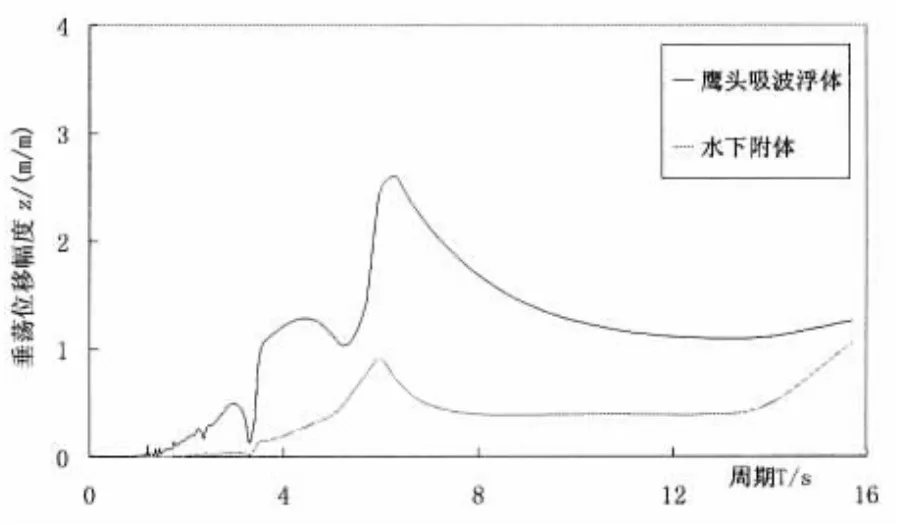
图10 垂荡荡运动的位移幅值Fig.10 Displacement amplitude in heaving

图11 纵摇运动的角度幅值Fig.11 Angle amplitude in pitching

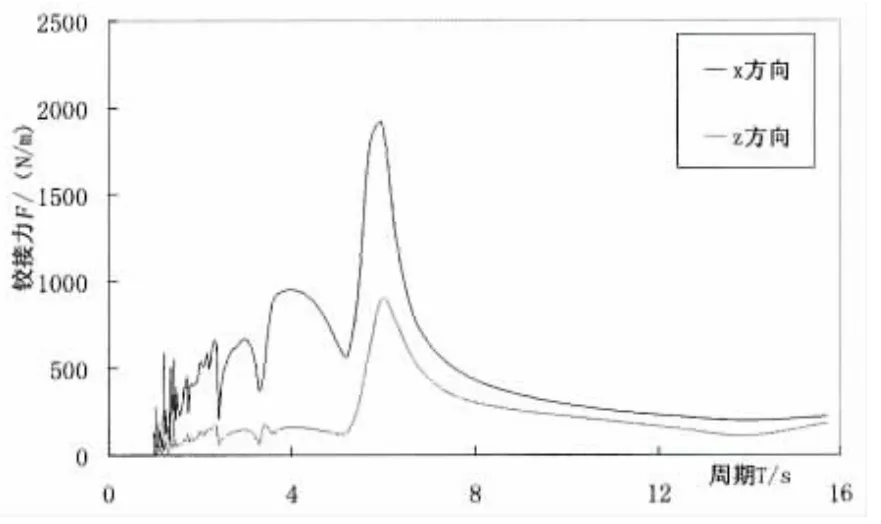
图12 铰接力Fig.12 Hinge force

图13 阻尼力Fig.13 Damping force

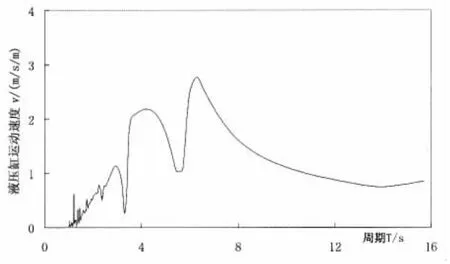
图14 液压缸运动速度Fig.14 Velocity of the hydraulic cylinder

图12描述了液压缸铰接在水下附体和鹰头吸波浮体上的铰接力。由于液压缸两个安装端点只在x轴、z轴有相对运动，则本文对这两个方向的分力进行了计算。两个方向的分力在数值上差距较小，变化趋势也基本一致，都是先增大后减小，再趋于定值。两个分力最大峰值几乎同时现在T=5.98 s，此时Fx=1 910.3 kN，Fz=898.3 kN。

图13、图14分别为液压缸提供最优外加阻尼下的阻尼力及对应的液压缸丝杠运动速度。最优外加阻尼力与速度之间为线性比例关系，两者随周期变化趋势一致，经历了三次先增后减。在T=6.28 s时，出现了最大阻尼力Fc=831.42 kN，以及液压缸的最大运动速度v=2.77 m/s。

4 结 论

本文对鹰式波浪能发电装置进行了水动力分析，建立了力学模型，通过数值模拟，获得了最优外加阻尼和最优俘获宽度比，确定了优化后的设计方案。得到以下结论，为装置的实海况样机设计提供理论参考依据：

（1）鹰式波浪能装置对波浪频率响应范围较宽，对周期4-8 s的入射波表现出良好的水动力学性能。

（2）水下附体作为稳定波浪能装置的基础结构，达到了设计效果。水下附体在做俘获波浪能的运动--纵摇运动时，受到的波浪力和波浪力矩均大于其它两种模态下的运动，但是附加质量与附加阻尼系数却大于两种模态下的数值，并且数值模拟的结果证实了水下附体各模态下运动幅值均较小。

（3）鹰式波浪能装置可实现高效俘获波浪能。在确定最优外加固定阻尼C=300 000 Ns/m后，在入射波周期为6.28 s时装置最高的转换效率达到η=385%。

（4）鹰头吸波浮体具有较强俘获波浪能的能力。当外加阻尼为最优值时，在单位幅值的入射波作用下，鹰头吸波浮体与水下附体在纵摇运动模态下的最大角度幅值差值达到18.36°。

[1]覃 岭,吴必军.双圆柱形浮体波能装置振动特性分析[J].船舶力学,2013,11:1253-1261. Qin Ling,Wu Bijun.Oscillating properties of a wave energy device consisting of double cylindrical floats[J].Journal of Ship Mechanics,2013,17(11):1253-1261.(in Chinese)

[2]赵海涛,沈家法.浮力摆式波浪能装置水动力性能的试验研究[J].船舶力学,2013,10:1097-1106. Zhao Haitao,Shen Jiafa.An experimental study on hydrodynamic performance of a bottom-hinged flap wave energy converter[J].Journal of Ship Mechanics,2013,17(10):1097-1106.(in Chinese)

[3]Sheng Songwei,You Yage,Wang Kunlin,Zhang Yaqun,et al.Research and development of sharp eagle wave energy convertor[C]//5th International Conference on Ocean Energy,4 November,2014,Halifax,Canada.

[4]盛松伟,游亚戈,王坤林,张亚群.10kW鹰式波浪能发电装置研究[C]//第二届中国海洋可再生能源发展年会暨论坛论文集.广东广州:国家海洋局,2013:378-384. Sheng Songwei,You Yage,Wang Kunling,et al.Research on 10kW sharp eagle wave energy convertor[C]//In:National Ocean Technology Center,eds.The 2th session of the China marine renewable energy development forum annual meeting proceedings.Guangdong Guangzhou:National Ocean Technology Center,2013:378-384.(in Chinese)

[5]张亚群,盛松伟,游亚戈,王振鹏,王坤林,吝红军.100kW一基多体漂浮鹰式波浪能发电装置模型试验研究[J].海洋技术学报,2014,04:73-80. Zhang Yaqun,Sheng Songwei,You Yage,et al.2014.Experimental study on a 100 kW one-base multi-buoy floating‘Sharp eagle’wave energy converter[J].Journal of Ocean Technology,2014,33(4):73-80.(in Chinese)

[6]王坤林,盛松伟,游亚戈,张亚群,姜家强,吝红军,叶 寅.“鹰式一号”漂浮式波浪能装置冗余监控技术研究[J].海洋技术学报,2014,04:62-67. Wang Kunling,Sheng Songwei,You Yage,et al.Research on the redundancy monitoring system of the‘Sharp eagle No. 1’floating wave energy converter[J].Journal of Ocean Technology,2014,33(4):62-67.(in Chinese)

[7]陈爱菊,游亚戈,盛松伟,彭 雯.鹰式波浪能装置旋转碰撞的损伤分析[J].新能源进展,2014,02:129-134. Chen Aiju,You Yage,Sheng Songwei,et al.Damage analysis of eagle wave energy converter in rotating-collision[J].Advance in New and Renewable Energy,2014,2(2):129-134.(in Chinese)

[8]陈爱菊,游亚戈,盛松伟,彭 雯.鹰式波浪能装置旋转碰撞的结构损伤过程研究[J].海洋技术学报,2014,04:6-11. Chen Aiju,You Yage,Sheng Songwei,et al.Study on the structural damage of the eagle type wave energy converter due to the rotating-collision process[J].Journal of Ocean Technology,2014,33(4):6-11.(in Chinese)

[9]Feng Peiyuan,Ma Ning,Gu Jiechong.Research on wave energy recovery by oscillating wings for energy efficient ship propulsion[J].Journal of Ship Mechanics,2013,17(9):1021-1030.

Hydrodynamic research on a Sharp Eagle Wave Energy Converter

ZHANG Ya-quna,b,YOU Ya-gea,b,SHENG Song-weia,b,WANG Wen-shenga,b
(a.Key Laboratory of Renewable Energy and Gas Hydrate;b.Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences,Guangzhou 510640,China)

According to Newton’s second law,mechanical analysis of multiple floaters Sharp Eagle wave energy converter is carried out.Based on microwave theory,the movement of every buoy in three modes couples each other,and there establishes a mechanical equations which is concerned with fluid forces,wave forces,damping force,hinge force,and so on.Hydrodynamic parameters of multiple buoys are solved when taking moving buoys as boundary conditions.Then through taking hydrodynamic parameters into the equations,optimum additional damping and optimal capture width ratio are calculated out.Following design optimizing,a plenty of data is obtained,such as displacements amplitude of each buoy in three motion modes (swing,heaving,pitching),damping force,hinge force,speed of the hydraulic cylinder.Research results provide theoretical reference and basis for Sharp Eagle WEC in design and manufacture.

Sharp Eagle wave energy converter(WEC);hydrodynamics;capture width ratio; optimal outer damping;optimization design

P75

：Adoi:10.3969/j.issn.1007-7294.2017.05.003

1007-7294（2017）05-0533-08

2016-11-22

国家青年自然科学基金项目（41406102）；海洋可再生能源专项资金（GHME2016YY01）

张亚群（1981-），女，博士，副研究员，E-mail：zhangyq@ms.giec.ac.cn；游亚戈（1956-），男，研究员。