归一化积相关Brisk图像配准算法

李秀华， 姚 佳

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)



归一化积相关Brisk图像配准算法

李秀华， 姚 佳

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

首先应用归一化积的相关系数进行图像块的匹配，对匹配成功的图像运用AGAST算法提取特征点，再将提取的特征点应用Brisk描述子进行描述，最后应用汉明距离对Brisk描述子进行匹配。

AGAST算法； Brisk算法； 归一化积相关

0 引 言

图像配准不仅在机器视觉、遥感、医学等众多领域已得到普遍应用，在军事方面也取得了令人瞩目的成绩。人类要从相同场景的两幅或多幅图像中获得更多的可利用信息时，就应该采取图像配准方法，对得到的图像进行处理。其中，Lowe[1]在2004年完善后的SIFT算法是一种效果较好也是比较成功的一种算法，但是该方法提取的冗余点多、计算复杂度较高。针对SIFT算法速度上的不足，Y.Ke[2]等结合主成分分析提出了一种PCA-SIFT算法，而Bay[3]等应用积分图像与黑森矩阵(Hessian)检测算子提出了SURF算法。随后，为了满足图像配准越来越高的实时性，Rublee[4]等在2011年提出了ORB算法，同年，Leutenegger[5]等提出了Brisk算法。在2012年，由王宏志[6]等将比值法与小波变换理论相结合的图像拼接方法改善了图像拼接的精度。

Brisk算子是一种新提出的二进制描述算子，并且同时具有尺度不变和旋转不变性。与SIFT、ORB等其他描述算法相比，Brisk算子在计算量和特征点匹配的时间方面也有明显提高，并且具有很高的性能。目前，在角点特征检测[7]、图像匹配[8]、图像识别[9]等领域,Brisk算法一直都是研究的热点。对Brisk算法的改进方法也层出不穷，分别在自适应阈值[10]、融合深度信息[11]、尺度空间[12]等多个方面进行了改进。因此,文中针对提取的特征点较为广泛，而提取的有些特征点在两幅图像的非重叠区域之中，会降低匹配特征点的效率。针对这个问题提出采用归一化积相关的方法来优化Brisk算法，用优化的算法对图像重叠区域提取的进行特征点匹配，以提高匹配效率和匹配正确率。

1 基于Brisk的图像配准方法

Brisk的图像配准方法主要包括3个环节：关键点提取、生成描述符和关键点匹配。

1.1 关键点提取

在检测环节，Brisk算法首先应用高斯差分滤波器(Difference of Gaussian， DOG)把图像构建成为N组S层的高斯差分金字塔，如图1所示。

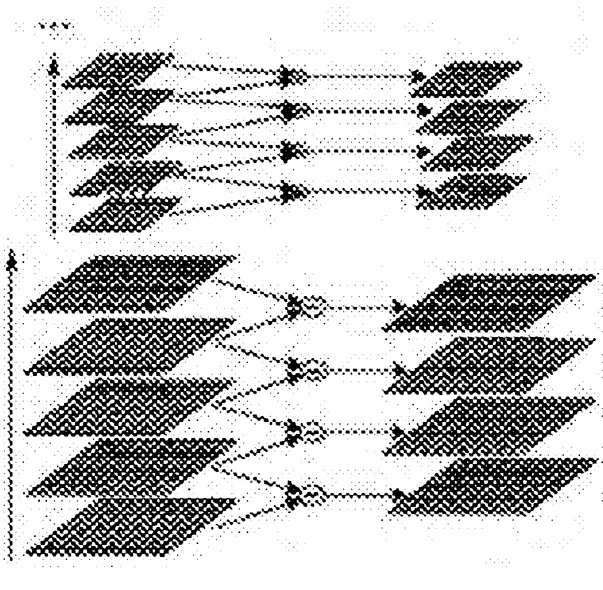
图1 高斯差分金字塔

然后分别在尺度空间金字塔的每层都使用AGAST角点检测算法，对AGAST算子检测出的关键特征点，根据检测出的响应值分布进行尺度空间的非极大值抑制，并应用曲线拟合的方法来计算图像亚像素精度的分布位置，如图2所示。

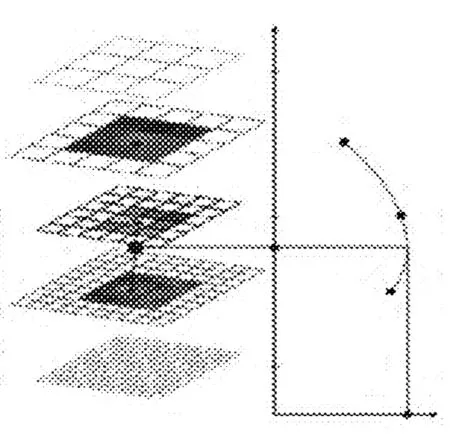
图2 尺度空间关键点检测

AGAST检测算子主要应用了模式为FAST9-16的检测算子，分别使用相同阈值T对各个图像组以及内插组来对关键点进行提取与检测，即在提取的关键点周围16个圆环点中至少存在9个连续的点，这9个连续的点一定要与中心点的像素值不同。对满足条件的关键点进行提取，并应用非极大值抑制方法来去除不稳定的特征点。

1.2 特征点描述子构造

描述符采样模式如图3所示。

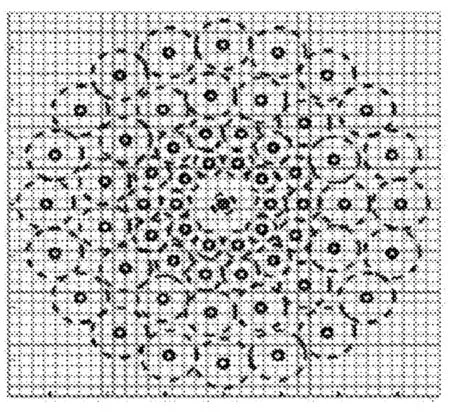
图3 描述符采样模式

在描述特征点过程中，为了确保描述子的旋转不变形，应对提取关键点的邻域像素对应用主方向归一化的方法，从而构造具有旋转不变性的描述子。因此Brisk采用图3所示的采样模式，即对关键点周围像素采样的固定采样模式。平滑采样点的方法是使用高斯函数的标准差，标准差到关键点的距离随着采样点到关键点距离的增长而增长，对采样点的划分采用采样点间灰度关系的方法，分为短距离点对和长距点对集合两类。关键点方向的计算主要是利用长距离点对集合，把采样点对的方向旋转到与关键点方向一致，生成二进制描述符是利用比较短距离点对间的亮度来生成的。

1.2.1 采样与主方向估计

为了提高描述子的抗干扰性与甄别性，在关键点的中心选择N个邻域点进行采样，对采样点的中心半径σ平滑就要采用方差为∂的高斯滤波器。对于N·(N-1)个采样点对g(pi,pi)其局部的梯度值g(pi,pj)通过平滑后的像素值来估计：

对所有的采样点集合：

其中，通过对长距离的像素设置距离阈值，通过迭代的方法可以估计出关键点的主方向。为了降低算法的运算复杂度和降低对关键点的整体梯度的影响，应基于对短距离的像素对梯度选取长距离的像素对。

1.2.2 构建描述子

必须对描述子进行旋转与尺度归一化，以保持Brisk描述子的旋转和尺度不变性。在算法中α=arctan2(gy,gx)为描述子主方向的角度，而描述子向量则采用像素值之比，此像素值之比是经过方向归一化后的短距离像素对之比。

描述子的构造采用了一些Brief的传统思想，但与之相比，本质上又有一些不同，在采样点的选取与相邻采样点的处理上也有一些不同的操作方法。首先，需要在归一化的半径范围内对采样点进行选取，也就是通过尺度的不同可以自动调整采样区域半径；其次，不会对相邻采样点之间的高斯滤波造成影响，进而描述子的鲁棒性也有了提高；最后，对采样点的像素对同时进行分组，分为两组，即长距离组与短距离组。由于采样数量偏少，分别计算长、短距离组描述子的主方向与描述向量。

1.3 描述子匹配

在生成Brisk描述符后，应用hamming距离来估量二进制描述符的相似性，进而实现提取关键点的匹配。然后应用RANSAC剔除误匹配，利用准确匹配关键点之间的对应关系估计图像的变换模型参数，最后应用变换矩阵对图像进行插值与变换。

2 基于归一化积相关的Brisk算法

2.1 归一化积相关算法

归一化积相关算法是一种经典的灰度相关算法，因此，具有不受比例因子误差的影响和抗白噪声能力强等优点。文中相似性度量值是以待配准图像与配准图像之间归一化积相关系数作为准则，通过逐步比较待配准图像搜索矩阵与原图像搜索矩阵之间的相关系数，得到其中的最大值点，也就是配准图像的最佳匹配位置。从而对匹配成功的图像进行特征点提取和特征点匹配，最后实现两幅图像的配准。首先，归一化积相关计算过程是计算相关矩阵，并且应用归一化积相关算法，通过寻找相关系数来确定矩阵之间的最大值点(即匹配点)。相关矩阵可以表示为:

设I为待配准图像，大小为W×H，T为配准图像，大小为M×N,则相关矩阵尺寸为(W-M+1)×(H-N+1),即包含了(W-M+1)×(H-N+1)个相关系数。坐标(x,y)处的待配准图像与原图像的归一化积相关系数的定义形式为：

2.2 归一化积相关的区域分割方法

文中应用区域分割的方法，也就是模板分块匹配的方法，通过设定不同的阈值，对分割后的小区域进行计算和比较，排除了不需要特征点提取的区域，以及提高了在特征点提取、特征点匹配的速度。区域分割法是应用分割图来代替原来的模板，通过计算图像分块区域的相关性的计算来判断匹配区域的位置，即图像配准的最佳匹配位置。

首先设定原图像为基准图f，待配准图像为实时图g，对实时图与基准图进行同样的方式按列划分，分块后的实时图分别为T1,T2，…,TN，基准图分别为S1,S2，…,SN，将实时图的N块图像分别记为搜索模板,并且分别与基准图的图像块进行交叉匹配。模板T在图像S上平移，(i,j)为左上角顶点的搜索图S中的坐标。设定最大相似性度量的值为一个常数，搜索图和模板的相似性通过度量函数来度量。在搜索过程中，采用归一化积相关匹配算法，计算模板块的相似度，如果模板块的相似度小于设定的最大相似性度量的常数，则对第2块模板块进行相似性度量的计算，并且与相似性度量的最大值进行比较，直到最后的相似性度量的结果大于设定的最大相似性度量的常数，则停止接下来的匹配计算，并对匹配成功的区域进行特征点的提取以及特征点的匹配。

2.3 图像的配准

在对图像进行匹配完成之后，应用对应的Brisk算法对匹配完成的图像进行图像配准，包括提取特征点，特征点描述子的生成以及最后的描述子的匹配。最后得到相应的图像配准结果。

3 实验结果

采用VS2010程序开发环境和OpenCV2.4.3库进行编程，使用的图片是在实验室采集的。为验证文中改进算法的有效率及准确性，将原算法与改进算法的特征点数、时间、正确匹配率的结果分别进行比较，从而得出配准的实验结论。

3.1 匹配结果对比分析

对比实验分别是原始算法与文中算法的实验结果对比和文中算法与原经典算法ORB的实验结果对比，文中采用3组图像进行实验，分别如图4～图6所示。

(a) 原始算法匹配结果 (b) 文中算法匹配结果

(a) 原始算法匹配结果 (b) 文中算法匹配结果

(a) 原始算法匹配结果 (b) 文中算法匹配结果

从原始图像的实验结果可以看出，匹配的特征点较多，特征点匹配对分布较为杂乱，而从文中改进算法的实验结果可以看到，特征点匹配对较为集中，匹配精确度较高。对比匹配结果可以看出，文中算法能够自动匹配两幅图像的重叠区域，并且只对重叠区域的特征点进行匹配，得到的匹配对分布均匀，拥有较好的实用能力。由于文中算法与原始算法都是对两幅图片的特征点进行提取，因此，对比结果中的特征点数相差无几，在精度分析的数据中不做显示。

文中对比实验结果为文中算法与原经典算法ORB的实验结果。本对比实验为更加突出原BRISK算法与文中算法的先进之处，依旧采用前3组图片进行对比实验，分别如图7～图9所示。

(a) 文中算法匹配结果 (b) ORB算法匹配结果

(a) 文中算法匹配结果 (b) ORB算法匹配结果

(a) 文中算法匹配结果 (b) ORB算法匹配结果

根据以上实验结果可以看出，OBR算法的匹配点数繁多，且匹配出的无效点较多，匹配正确率较低。针对文中算法对特征点的匹配区域比较集中，且匹配正确率较高，在实际应用方面有很大优势。

3.2 匹配精度分析

文中的配准精度客观评价标准参见文献[13]，采用均方根误差的评价标准进行评价。本实验采用阈值为60的Brisk算法参与对比实验。两种方法的时间统计结果对比分析见表1。

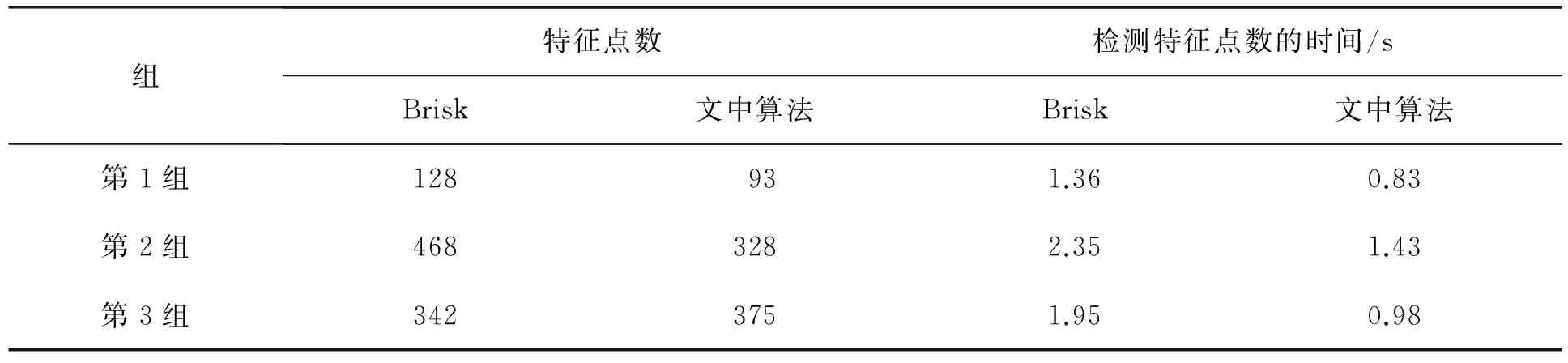
表1 原始算法与改进算法特征点检测的时间统计

在匹配阶段，文中算法由于采用归一化积进行图像匹配，最后又计算了汉明距离的匹配正确率，可能在计算速度上有所降低，但随后进行的特征点匹配则大大降低了匹配时间，通过部分图像的特征点对的匹配及检测汉明距离以确定匹配的正确率，剔除了大量的非匹配点。对3组实验图像进行特征点匹配的正确率与时间统计对比分别见表2和表3。

表2 文中算法特征点匹配的正确率和时间统计

表3 Brisk算法特征点匹配的正确率和时间统计

通过对比实验可以看出，文中算法不仅提高了执行效率，达到了预先的理想效果，并且与BRISK匹配速度基本一致，但在总体匹配正确率上文中算法有着明显的优势。

通过表2、表3的对比可以看出，文中算法不仅提高了匹配效率，而且大大提高了匹配正确率。

表4 文中算法与ORB算法特征点匹配的正确率和时间统计

表5 ORB算法特征点匹配的正确率和时间统计

通过表4、表5文中算法与ORB算法的对比数据可以看出，文中算法不仅在运算速度上比ORB算法快，并且在特征点匹配的正确率上有着明显优势。

4 结 语

针对原始Brisk算法的特征点检测过于繁多、特征点匹配效率过低等问题，提出了一种改进的Brisk算法。实验结果表明，通过改进原始的Brisk算法能够减少配准时间，提高配准效率与配准的准确性，并且也很好地继承了原始算法的优点。

[1] Lowe D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision,2004,60(2):91-110.

[2] Ke Y, Sukthankar R. PCA-SIFT: A more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on,2004,2(2):506-513.

[3] Bay H, Tuytelaars T, Van Gool L. Surf: Speeded up robust features [M]. [S.l.]: Computer Sion-ECCV,2006:404-417.

[4] Rublee E, Rabaud V, Konolige K, et al. ORB: an efficient alternative to SIFT or SURF [M]. [S.l.]: Computer Vision (ICCV),2011:2564-2571.

[5] Leutenegger S, Chli M, Siegwart R Y. BRISK: Binary robust invariant scalable keypoints [M]. [S.l.]: Computer Vision (ICCV),2011:2548-2555.

[6] 王宏志,李美静,张立伟，等.畸变图像拼接算法研究[J].长春工业大学学报：自然科学版，2012,33(5):533-536.

[7] 曹建,谢晓方,梁捷，等.基于BRISK改进的快速角点特征算法[J].舰船电子工程，2013,5:44-47.

[8] 卫星,樊绍胜,高山，等.基于BRISK的图像快速匹配与变换算法[J].电子测量技术，2015,38:43-47.

[9] 桂振文,刘越,陈靖，等.一种适用于智能手机的图像识别算法[J].电子学报，2014(8):1487-1494.

[10] 石祥斌,孙奇,张德园，等.一种自适应阈值分块BRISK的图像配准方法[J].沈阳航空航天大学学报，2014,31:65-72.

[11] 张恒,刘大勇,刘艳丽，等.融合深度信息的BRISK改进算法[J].计算机应用，2015,35(8):2285-2290.

[12] 何林阳,刘晶红,李刚，等.改进BRISK特征的快速图像配准算法[J].红外与激光工程，2014,43:2722-2727.

[13] 许斌，徐万朋,陈向宁，等.基于BPT分割的SAR与可见光图像配准方法[J].四川兵工学报，2014,35:105-108.

Normalized product correlation Brisk image registration algorithm

LI Xiuhua， YAO Jia

(School of Computer Science and Engineering, Changchun University of Technology, Changchun 130012， China)

The normalized product correlation coefficient is applied for image block matching, and the feature points of matched images are extracted with AGAST algorithm. Then the feature points are described with Brisk descriptor which is matched with Hanming distance.

AGAST algorithm； Brisk algorithm； normalized product correlation.

2016-12-28

吉林省科技厅基金资助项目(KJT2016-1)

李秀华(1971-)，女，汉族，吉林桦甸人，长春工业大学副教授，博士,主要从事智能控制与图像处理方向研究,E-mail:lixiuhua@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2017.2.12

TP 301.6

A

1674-1374(2017)02-0167-07