基于质量守恒边界条件的液压缸织构表面空化模型
毛 阳,曾良才,2,卢 艳
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2. 武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
基于质量守恒边界条件的液压缸织构表面空化模型
毛 阳1,曾良才1,2,卢 艳1
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2. 武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
传统的雷诺边界条件没有考虑到微凹坑织构中存在的空化现象,较难准确预测织构化表面的润滑特性。本文以液压缸缸筒-活塞摩擦副为研究对象,基于质量守恒的边界条件,建立均匀分布的微凹坑织构表面油膜压力与变密度两者之间的空化数学解析模型,采用中差分模型和迎风算法进行数值离散,得到摩擦副中油膜的压力分布以及空化生成的位置。FLUENT仿真结果验证了该空化模型的有效性。
液压缸;表面织构;空化模型;质量守恒边界条件
利用表面织构技术能改善活塞与缸筒的润滑性能,大幅度降低摩擦阻力,增大摩擦副内的油膜支撑力,形成动压润滑,是提高液压缸往复动态特性的一种有效途径[1]。织构表面油膜会产生空化现象[2],空化现象是织构表面形成动压润滑的主要因素[3-4]。目前关于织构表面动压润滑流场一般采用雷诺方程来求解,然而,经典雷诺方程的求解通常将密度设为一个常量,忽略了空化现象的影响,使得求解结果与实际工况不相符。另一方面,由于空化试验难度大,使得数学建模缺乏可靠的对比试验。为此,本文在采用质量流量守恒边界条件约束的基础上,通过对经典雷诺方程进行修正,考虑织构内部的空化现象,对摩擦副进行数值解析,引入密度变量γ,建立基于表面织构的压力与变密度两者之间的新型空化理论数学模型,并通过FLUENT建立Mixture气液两相流模型,对本文模型的有效性进行验证。
1 摩擦副织构空化数学模型的建立
1.1 织构几何模型
以液压缸缸筒-活塞摩擦副为研究对象,在缸筒内壁加工均匀点状分布的微凹坑织构;活塞表面为非织构面,作往复运动。截取部分织构化的缸筒内表面与活塞组成摩擦副,如图1所示,假定活塞与缸筒存在理想的均匀环形间隙,即活塞对中,活塞与缸筒相对平行。
截取图1中的一个织构单元进行分析,其示意图如图2所示。摩擦副两个表面之间的距离为油膜厚度h,微织构凹坑宽度与单元体长度L的比值为宽度比α,微织构凹坑深度与活塞和缸筒间的间隙h0的比值为深度比β。假设空化存在于区间[a,b],将流场视为不可压缩流体,油液从左端流入,右端流出,流体的黏度系数η为常值,则油膜厚度可分段表示为

(1)
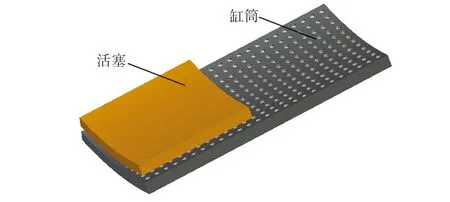
图1 摩擦副表面微织构几何模型
Fig.1 Geometrical model of friction pair surface micro-texture
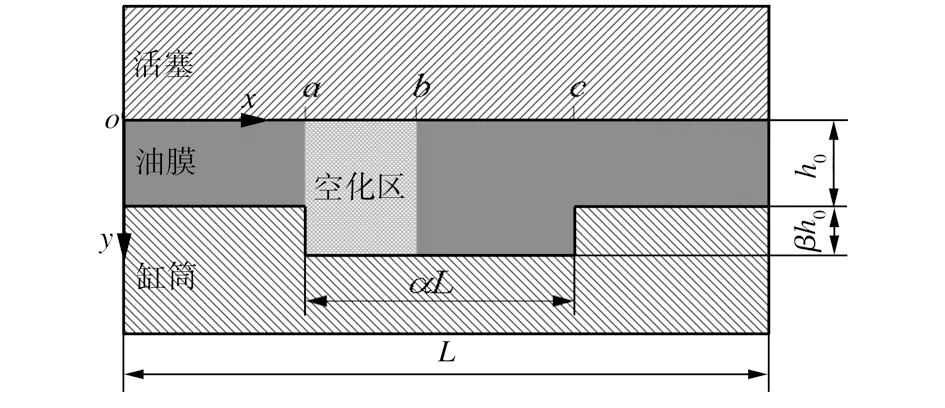
图2 微织构单元示意图
1.2 空化模型的建立
以质量流量q守恒为边界条件对流场进行数值建模,公式如下[5]:
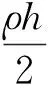
(2)
式中:ρ和p分别为流体的密度和压力;U为流体流动的速度。
将式(2)对x求导得:
(3)
引入新的变量γ来表示密度的变化量,设γ=1-ρ/ρ0,则存在以下等式:
从企业数量来看,我国西部地区融资租赁行业在西部整体呈现增长趋势,2013年仅有35家融资租赁公司,截止2017年底有了296家,5年内增长了约8.5倍,企业数量平均增长率在80%以上。但从数量百分比上看,企业的数量占有率相对较少,西部地区12个省级单位,2017年底仅占有3.26%,西部地区融资租赁发展潜力巨大。西部现有企业中,外资租赁公司一家独大,有258家,占到总企业数量的87.16%;其次是内资租赁公司,有27家,占到企业数量的6.82%;再次是11家金融租赁公司,占到企业数量的6.02%。该特点和全国其他区域是相似的,外资租赁公司在中国一家独大。
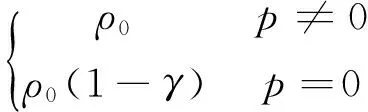
(4)
式中:ρ0为未产生空化时油液的密度,为常量。
由此可得:
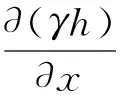
(5)
当油液没有产生空化时,油液的密度值为常值,即ρ=ρ0,此时γ=0;当产生空化时,空化区域压力值p=0,p=0。因此,不论油液产生空化与否,式(5)中的第一项均等于0,故式(5)可化简为
(6)
其中,p≥0,γ≥0,pγ=0。
只考虑织构纯往复运动情况时,雷诺方程可写为一维二阶偏微分方程,其标准式如下:
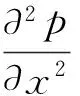
(7)
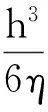
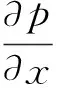
(8)
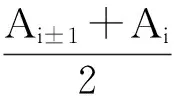

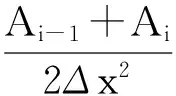
建立系统的离散化线性补偿方程,最终得到考虑空化效应的修正雷诺方程如下:
Yp=fγ+Z
(9)
其中,p≥0,γ≥0,pγ=0。
2 空化模型验证
2.1 CFD模型的建立以及参数设置
利用FLUENT 软件进行流体模拟计算,首先利用ICEM进行流动区域几何模型的构建、边界条件的设置以及网格的生成,并输出用于FLUENT求解器计算的格式,然后利用多相流Mixture模型对空化织构进行求解计算。设定网格尺寸为10-3mm×10-3mm,收敛值设置为10-5。为简化仿真实验,取一个织构单元(见图2)进行分析。仿真计算参数如表1所示。
模型的边界条件设置为:流体入口与出口处分别定义为周期边界条件,下表面设置成静止面,上表面设置为运动面。

表1 空化模型仿真参数
2.2 仿真结果与分析
摩擦副间油膜流场中气体体积分数云图如图3所示。由于宽度比大,为了显示清楚,截取单个织构单元中具有典型代表意义的3段(图3中(a)、(b)、(c))进行放大分析,分别代表织构凹坑下壁面的最左端、中间气泡消失段以及凹坑下壁面的最右端。由图3中可以看出,在织构凹坑内确实产生了一定体积分数的气体,即有空化现象产生。
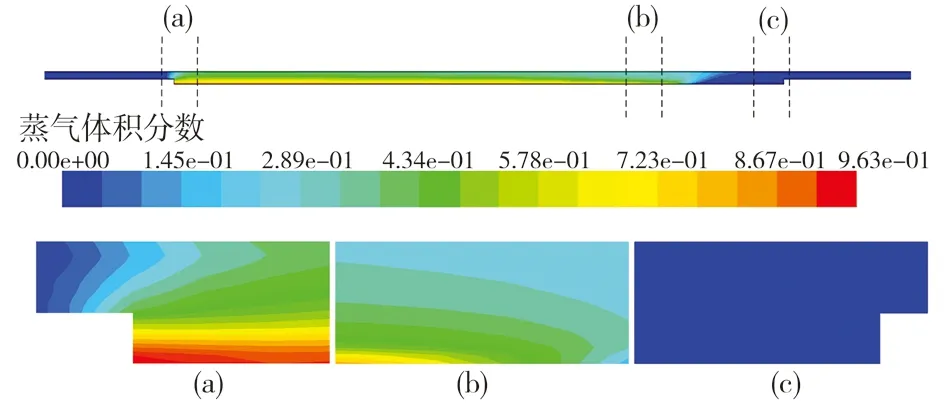
图3 油膜中气体体积分数云图
同样地,截取单个织构的压力分布示意图如图4所示。从图4中可以看出,压力的最大值出现在靠近出口处的织构凹槽壁面位置。
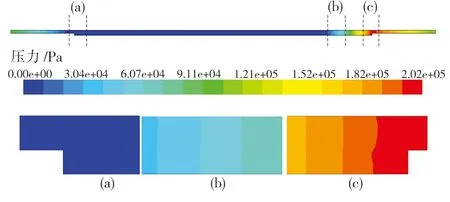
图4 油膜压力分布云图
2.3 数值计算结果与仿真结果的对比
在MATLAB中,通过对空化模型(式(9))编写计算代码来计算织构表面油膜的压力分布,参数设置与仿真中的相一致。模型计算结果与仿真结果进行比较,结果如图5所示。由图5中可见,空化模型数值求解与仿真实验所得压力分布具有很好的一致性。

图5 压力的数值解与仿真解对比
Fig.5 Comparison of the numerical solution with the simutation solution to the pressure
织构内部压力值等于0的区域即为织构内部空化产生的区域。由图5中可以明显地看出,两种方法求得的织构产生空化的位置与在数学建模中的假设相一致,表明修正后的雷诺方程空化模型可以很好地预测空化产生的位置。压力极值产生在靠近出口处的织构凹槽壁面位置,与仿真结果相同,表明本文考虑空化现象对雷诺方程的变密度修正方法是准确有效的。
3 结语
通过采用数学建模与有限元仿真两种方法,本文以液压缸缸筒-活塞摩擦副为研究对象,构建了直线运动的表面微织构流场的空化模型。采用修正后的雷诺方程对织构表面油膜流场进行计算,可以预测油膜中空化发生的位置、表面压力值的分布等。较仿真而言,数值模型求解方便,仅通过修改数学参数便可取得,更加适用于前期研究。通过控制油膜中气体形成与流动的演化,可以改善摩擦副的润滑状态,实现降低摩擦、减缓磨损、延长摩擦副使用寿命并减少润滑剂损失,符合绿色节能制造理念,可为实现伺服液压缸等的高速化提供理论与技术支撑。
[1] Mao Y, Zeng L C, Lu Y. Modeling and optimization of cavitation on a textured cylinder surface coupled with the wedge effect[J]. Tribology International, 2016, 104:212-224.
[2] Buscaglia G C, Talibi M E A, Jai M. Mass-conserving cavitation model for dynamical lubrication problems. Part I:mathematical analysis[J]. Mathematics and Computers in Simulation, 2015,118:130-145.
[3] Buscaglia G C, Talibi M E A, Jai M. Mass-conserving cavitation model for dynamical lubrication problems. Part Ⅱ: numerical analysis[J]. Mathematics and Computers in Simulation, 2015, 118:146-162.
[4] Wahl R, Schneider J, Gumbsch P. In situ observation of cavitation in crossed microchannels [J]. Tribology International, 2012, 55:81-86.
[5] 温诗铸, 黄平. 摩擦学原理[M]. 北京:清华大学出版社, 2002.
[责任编辑 郑淑芳]
Cavitation model of the textured cylinder based on mass conservation boundary conditions
Mao Yang1, Zeng Liangcai1,2, Lu Yan1
(1. Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education,Wuhan University of Science and Technology,Wuhan 430081, China; 2. Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering,Wuhan University of Science and Technology, Wuhan 430081, China)
The traditional Reynolds boundary conditions fail to consider the cavitation phenomenon in the pits of micro-texture and thus cannot accurately predict lubricating property of the micro-textured surface. In this paper, the hydraulic cylinder-piston friction pair was studied based on the mass conservation boundary conditions. The analytic mathematical model of cavitation between oil film pressure and variable density on the textured surface with uniformly-distributed pits was established. The finite difference model and the upwind scheme were used for numerical discretization to obtain the pressure distribution and the cavitation location. FLUENT simulation has proven the effectiveness of the cavitation model.
hydraulic cylinder; textured surface; cavitation model; mass conservation boundary conditions
2017-03-16
国家自然科学基金资助项目(51475338,51405350).
毛 阳(1990-),女,武汉科技大学博士生.E-mail:maomao0738@qq.com
曾良才(1964-),男,武汉科技大学教授,博士生导师.E-mail:zengliangcai@wust.edu.cn
10.3969/j.issn.1674-3644.2017.03.010
TH117
A
1674-3644(2017)03-0213-04

