试卷识别码的集成设计与识别算法

吕书龙， 刘文丽

(福州大学 数学与计算机科学学院， 福建 福州 350116)

试卷识别码的集成设计与识别算法

吕书龙， 刘文丽

(福州大学 数学与计算机科学学院， 福建 福州 350116)

设计一种可简单书写的数码数字，并将其作为学号识别码直接集成在试卷上，有效地实现试卷与学生的一一对应关系.分析纸质扫描试卷识别码的识别算法，处理了识别中可能出现的多种异常情况，并将该设计和算法应用到选择类试题答案的自动识别和批阅中.实测结果表明：所提出的集成设计，具有占用空间小、连写简便、识别快速、识别率高和低成本等特点.

网络阅卷系统; 数码数字; 识别算法; 集成设计

目前，大部分高校的全校性基础课依然实行统考和手工流水阅卷，阅卷的公平性,试卷的质量分析,试卷及试题的统计分析、查卷,试卷存储,专家评估等管理问题较为突出.商业网络阅卷系统在全国性的大型考试中应用较好，但是对于各高校每学期数量众多的考试而言，管理成本极高，推行困难.因此,如何在不改变现有考试模式和考生答卷习惯的前提下，研究适合高校运作的低成本、高效率的网络阅卷系统是有意义的.在网络阅卷系统的软件扫描识别部分，最关键的基础工作应该是识别考生身份的，实现考生与答卷的关联.针对书写比较规则的数字，一些学者给出了不同的识别方法和采集方式[1-6]，取得一定成效.但在实际情况中，学生手写的学号花样百出，情况复杂，更需要灵活性和规范性的填写设计，异常的预判和对应的措施等.本文提出将试卷识别码、选择题识别、试卷和答卷集成在一份试卷上的一体化试卷模式，并统一了学号识别码和选择题答案的识别算法.

1 数码学号与一体化试卷版式设计

1.1 数码学号的设计

学校分配给学生的学号都是由阿拉伯数字构成的，因此，学号可作为唯一的识别码.由此提出了6点连线的书写规则，每个数字通过6个点的连线构成，并形象地称为数码学号，如图1所示.设计中给出6个点，直观且便于构成7个连通区以待识别，另外，也可以规范学号的书写，减少出错.

图1 数码学号书写规则Fig.1 Writing rules of digital student ID

经大量实际测试得到，每个数字的宽度和数字间的间隔相等，且宽度为4 mm，高度为8 mm.这样的设计比较符合书写习惯也容易识别,如果太高、太宽极易造成连线歪斜，而太窄、太小又不利于图像处理，又影响识别的准确性.

1.2 试卷版式设计

试卷版式首页和学生信息区新旧版对照示意图，如图2，3所示.由图3(b)可知：在装订线外，新版学生信息除保留旧版所有的信息外，在右侧增加了数码学号区域.该区域上端留给手写学号，下端用来书写数码学号，并在左侧给出书写范例.

该设计有如下两个主要目的：1) 手写学号为连写数码学号提供参照，大大降低书写错误率；2) 如果机器识别失败，还有机会通过手工识别加以纠正.

(a) 旧版 (b) 新版 图2 试卷版式首页示意图Fig.2 Sketch map of examination paper

(a) 旧版

(b) 新版图3 学生信息区示意图Fig.3 Sketch map of student information area

对首次使用该版式的学生进行大量测试，结果表明,连写完一个9位学号，平均用时40 s；而对熟悉该版式的学生而言，耗时不超过30 s.因此，数码学号的引入对学生作答时间的影响可忽略.测试表明，平均书写错误率低于1%，主要原因归结为考试紧张和不按范例书写.对于这个问题，一方面,可以在开考前提醒;另一方面,可在每个考场多备几份空白卷以便更换.即使不更换，后期也可由人工识别处理.

因此，只需要对试卷版式和客观题选项编码作细微的调整，就可以将上述数码学号的设计应用到选择题上.将常规的选择题选项数字化，比如选择题中4个选项一般由(A，B，C，D)构成，为了便于识别处理，将这4个选项编码映射成 (1，2，3，4)；判断题的错与对也可以映射成(0，1).然后，在客观题区域下方，留出空间作为客观题的填涂区域，如图4所示.

图4 选择题区域Fig.4 Area of multiple choice questions

2 识别算法及异常情况分析

2.1 识别流程与算法描述

数码学号是实现考生与试卷自动关联的唯一标示码，它直观易懂.总体上，每个数字可由6个点的适当连线构成，所有可能的7条连线定义成7个连通区域；然后，通过每个区域的连通性来实现数字的识别，如图5所示.

图5 连通区域和数字示意图Fig.5 Connected regions and sketch maps of numbers

设基于连通性的数码数字串含有n个数字，则识别流程有如下5个主要步骤.

步骤1 在扫描的试卷图片中，提取数码数字串所在区域位图，进行合理的二值化.此时，位图转化成0～1数字矩阵(0代表白色，1代表黑色)，记为MS.

步骤2 通过行扫描和列扫描，去掉矩阵MS外层多余的空白行和空白列,得到最小的外接矩阵，仍记为MS.

步骤3 从矩阵MS中依据设计尺寸提取每个数码数字的子矩阵，并同样通过行列扫描得到其最小的外接矩阵，记为Mi，i=1，2，…，n.

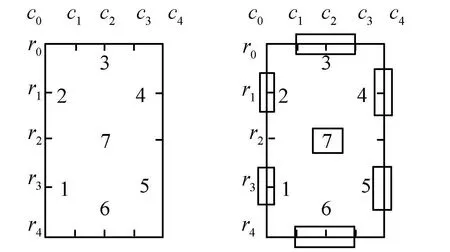
(a) 连通性 (b) 关键坐标点图6 数字矩阵Mi的连通判定示意图Fig.6 Sketch map of connection of digital matrix Mi

步骤4 数字矩阵Mi的连通判定示意图，如图6所示.将Mi矩阵行列各4等分，横向自左向右依次为c0，c1，c2，c3，c4，其中,c0和c4为左右边界；纵向自上而下依次为r0，r1，r2，r3，r4，其中,r0和r4为上下边界.Mi矩阵的中心坐标为(c2，r2)，左上角为(c0，r0)，右下角为(c4，r4).理论上通过矩阵的关键行列坐标点附近的非零值可确定所在区域的连通性.若在矩阵Mi的行列坐标为(c0，r3)附近存在非零值则可判定图6的区域1为连通.以此类推，行列坐标点(c0，r1)，(c2，r0)，(c4，r1)，(c4，r3)，(c2，r4)，(c2，r2)附近的非零值可分别确定区域2到区域7的连通性，如图6(a)所示.由于书写难以达到理论上的横平竖直，所以应分析关键坐标点邻域中的非零值，如图6(b)所示.

步骤5 由上述连通性的判定，再根据图5的规则，可确定Mi所对应的数字.其对应规则为：区域1，2连通或区域4，5连通则判定为数字1；区域1，3，4，6，7连通则判定为2；区域3，4，5，6，7连通则判定为数字3；依此类推.若把区域的连通记为1，不连通记为0，则每个数字就对应了一个长度为7的0/1数字串，例如,“1100000”和“0001100”代表数码数字“1”.

重复步骤3～5，可识别完所有子矩阵对应的数字，完成整个数码数字串的识别.

2.2 异常情况及应对措施

在实际考试中，数字连写不规范、扫描走纸发生倾斜都可能出现异常情况，包括但不限于以下6种异常情况：1) 连写数字时，出现连线弯曲、越界、轻微涂改等；2) 连写数字随意、不完整或不规则；3) 采用铅笔填涂时描线过淡，数字模糊；4) 识别区域有较多笔尖接触导致的杂点；5) 扫描试卷可能出现小偏斜(偏斜度约1°)、折页等；6) 学生忘记连写学号.

异常情况1,4,5会导致提取的最小外接矩阵与标准尺寸不符；异常情况2,3导致连通性判别出错；异常情况6导致无法识别.除了异常情况6必须人工介入外，其他几种异常都可以在算法上进行自适应调整，以避免可能出现的误判情况.文中引入关键点邻域扩充、模糊识别和灰度阈值随机提升3种措施，对算法进行完善和改进.

1) 改进1.关键点邻域扩充.扫描试卷采用的分辨率为200 DPI，则4 mm对应的图片像素大致为34 px，可保证在边界和关键点处±4个像素的扩充邻域不互相重叠，如图6(b)所示.针对区域1，可将关键坐标点(c0，r3)放大到矩形区域(c0，r3-4，c0+4，r3+4)，再通过统计该区域中像素1的占比或总量不小于8判定区域1的连通性，其他区域的连通可依此类推.经过修正后，可显著消除异常情况1,4,5，可部分消除异常情况2，使得连通性判定更加合理稳健，数码数字的识别率也得到大幅提升.

2) 改进2.引入模糊识别.比如区域1，2连通或区域4，5连通均可对应数字1；区域1，3，4，7连通可对应数字2.多个数字的模糊对应，如图7所示.模糊识别部分消除了异常情况2中连写数字的不完整情况.

图7 模糊等价图Fig.7 Fuzzy equivalence graph

3) 改进3.灰度阈值的随机提升.部分考生采用铅笔连写数码学号，由于描笔过淡，色彩对比不够明显，导致经典的OTSU算法[7-8]计算的平均灰度阈值偏小，使得二值化后的图像信息损失较多，从而影响了连通性识别.用铅笔填涂学号的二值化前后的图像对比，如图8所示.图8中：经典OTSU算法得到的平均灰度阈值是209.灰度阈值为224时的二值化图像，如图9所示.

(a) 原图 (b) 二值化后图图8 二值化前后的图像对比示意图Fig.8 Graph comparison before and after binarization process

图9 提升阈值后的二值化图像Fig.9 Binary image after lifting threshold value

由图8，9的对比可知:选择合适的灰度阈值对于二值化是非常重要的.经大量此类图像的实测统计，经典OTSU算法得到的灰度阈值平均偏小10个灰度级，均方差约为2，故对OTSU算法的平均灰度阈值作简单随机调整，即

改进灰度阈值=OTSU平均灰度阈值+rnorm(10，2).

(1)

式(1)中:10和2分别为正态分布的均值和标准差；rnorm为正态分布随机数的生成函数.

规则的手写数字是系统顺利运行的一个基本前提和保障，若结合手写数字的识别算法[9-10]，将有助于解决上述异常情况1～5.但系统需要实时高效地处理大量的试卷识别，故暂时未引入手写识别的规则，上述处理方案是多方因素综合考虑的权衡选择.

3 实测结果与分析

扫描仪器：夏普MX-M753N数码复合机，分辨率为200DPI，双面扫描成JPG图像， 扫描速度是每分钟20份的A3幅面.主机性能：Intel(R)Core(TM)i5-3470CPU@ 3.2GHz，内存8.0GB；硬盘 1TB/7 200转/64MB.测试工作：试卷图片读取，数码学号区域提取，数码学号识别，学号与学生信息表关联.A3幅面的试卷正反面采用200DPI扫描成2张JPG图像，每张图片像素尺寸为3 307px×2 338px， 大小约为950KB，图片尺寸是试卷尺寸的2倍，该尺寸图片达到网络阅卷清晰度的要求.

表1给出基本测试数据.由表1可知：数码学号的识别耗时极少，主要时间耗费在读写JPG图片，并转成内存位图上.对于规则的学号填涂，连通性算法的识别正确率可达100%.

表1 测试结果Tab.1 Test results

表1实测数据中，学号识别正确率不足100%，经统计分析，主要原因是书写严重偏离书写规范、胡乱涂改或空白不写.这类问题的出现是小概率事件，但似乎又在每次考试中发生.因此，有必要加强考前培训以降低此类问题出现的概率.另外，对于严重偏离书写规范或有涂改的前提下，参考手写数字的识别或机器识别来研究更稳健更智能的识别算法也未尝不可.

4 结束语

所提出的试卷版式和数码学号的设计，具有占用空间小，连写简便，识别快速，识别率高、成本低等特点，为网络阅卷系统的实现与推广奠定了坚实的基础.网络阅卷系统目前运行良好，后期将对智能识别算法、任务调度策略、系统安全性、网络负载均衡、阅卷质量实时监控，以及试题和试卷的全方位的统计分析问题作进一步深入的探索和研究.

[1] 罗理，王峰.网上阅卷系统中八字码识别方法的研究与实现[J].计算机与数字工程，2007，35(12):40-42.

[2] 邓富强.特定区域数字识别系统的实现[J].电子技术与软件工程，2015(15):103.

[3] 崔行臣，段会川，王金玲,等.数显仪表数字实时识别系统的设计与实现[J].计算机工程与设计，2010，31(1):213-217.

[4] 范新南，郭建甲，苏丽媛.基于数学形态学的数字仪表数码识别快速算法[J].计算机测量与控制，2006，14(11):1589-1590，1593.

[5] 巩玉滨，杨红娟，张运楚，等.一种数显仪表数字字符识别方法研究[J].山东建筑大学学报，2011，26(2):134-137，177.

[6] 马礼，慈林林，张永梅，等.不规则数码脱机识别技术[J].小型微型计算机系统，2003，24(5):940-942.

[7] OTSU N.A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems， Man and Cybemetics，1979，9(1)：62-66.

[8] 吕俊哲.图像二值化算法研究及其实现[J].科技情报开发与经济，2004，14(12):266-267.

[9] 柳回春，马树元，吴平，等.基于结构特征的手写体数字识别算法[J].计算机工程,2002,28(11):28-29，60.

[10] 吴少泓，王云宽，孙涛，等.基于距离分布直方图的数字识别算法[J].计算机应用，2012，32(8):2299-2304.

(责任编辑： 陈志贤 英文审校： 吴逢铁)

Integrated Design and Recognition Algorithm of Identification Codes in Examination Paper

LYU Shulong， LIU Wenli

(College of Mathematics and Computer Science， Fuzhou University， Fuzhou 350116， China)

It designs a simple and easy-writing digital numbers and takes them as recognition identification codes integrated in the examination paper. This design effectively realizes the one-to-one correspondence between the student and his examination paper. It analyzes the recognition algorithm of the digital numbers in scanned examination paper, and solves several abnormal conditions in the recognition process. The design and recognition algorithm are also applied to the automatic identification and marking of objective questions. The experimental results show that the proposed design and recognition algorithm have the advantages of small occupied space, easy-writing, rapid recognition, high rate of recognition and low cost etc. Keywords：network-based scoring system; digital numbers; recognition algorithm; integrated design

10.11830/ISSN.1000-5013.201703020

2016-11-15

吕书龙(1977-)，男，副教授，主要从事应用统计与软件设计的研究.E-mail:wujispace@126.com.

国家自然科学青年基金资助项目(11301084)； 福建省本科高校教育教学改革研究项目(JAS151395)； 福州大学第九批高等教育教学改革工程项目(0360-52001024， 0360-52001069)； 福州大学研究生优质课程建设项目(0480-52004634)

TP 311； TP 391

A

1000-5013(2017)03-0397-05