汽车电子节气门位置最优预见控制
张邦基 陈志强 田 阳 张 农 王 明
(1.湖南大学汽车车身先进设计制造国家重点实验室, 长沙 410082;2.悉尼科技大学工程与信息技术学院, 悉尼 NSW 2007; 3.合肥工业大学汽车与交通工程学院, 合肥 230009)
汽车电子节气门位置最优预见控制
张邦基1陈志强1田 阳2张 农3王 明1
(1.湖南大学汽车车身先进设计制造国家重点实验室, 长沙 410082;2.悉尼科技大学工程与信息技术学院, 悉尼 NSW 2007; 3.合肥工业大学汽车与交通工程学院, 合肥 230009)
基于线性二次型最优控制理论和线性矩阵不等式处理方法,提出一种适用于汽车电子节气门的位置离散最优预见控制算法,该算法仅通过一组滑动电位计来测量节气门阀片角度位置实现闭环控制。针对节气门的实际使用环境,建立了离散化的节气门状态空间模型,利用状态转移法构建了包含目标信号的扩大误差系统;考虑实际系统中节气门物理参数难以辨识的特点和外部扰动力矩等不确定因素的影响进行了仿真,并基于快速控制原型技术进行了试验验证。仿真和试验结果均表明,所设计的位置最优预见控制算法能够快速准确地跟踪目标开度信号,增强了电子节气门控制系统的稳定性和鲁棒性。
汽车电子节气门; 位置跟踪; 最优预见控制; 快速控制原型; 鲁棒性
引言
电子节气门是在传统机械节气门基础上采用电动执行机构实现电子控制,从而避免传统节气门与加速踏板通过机械连接致使节气门开度仅受驾驶员控制的缺点。它是发动机管理系统中的重要部件,是实现发动机全电控的基础,因而得到广泛应用[1-4]。电子节气门控制系统(Electronic throttle control system,ETCS)由节气门最佳开度计算和节气门阀片位置跟踪控制两部分组成[5]。由于节气门的位置跟踪控制效果直接影响发动机的性能,因此,采用何种算法保证其具有较高的鲁棒性、较快的响应速度和良好的位置跟踪等特点,成为诸多学者的研究热点[6-11]。
预见控制可利用已知的未来目标或干扰信息来改善系统的性能,并对其进行前馈补偿,使得系统能够实时无误差地跟踪目标信号[12-13]。目前,预见控制已在车辆悬架[14-15]、车道辅助自动控制[16]、电磁全可变气门[17]及混合动力汽车能量管理[18]等领域取得广泛研究。本文建立离散化的电子节气门状态空间模型,采用状态转移法构建包含目标信号的扩大误差系统,在此基础上,利用线性二次型和线性矩阵不等式方法设计最优预见控制器,并在仿真过程中考虑节气门参数不确定性和空气扰动的影响。
1 电子节气门控制系统
ETCS包括节气门体与两级减速机构、复位弹簧、直流电动机、电动机驱动器、发动机电控单元(Engine control unit, ECU)、油门踏板、节气门和油门踏板位置传感器,如图1所示。ECU可根据油门踏板位置以及发动机转速、工作模式、挡位和车速等信息,计算出节气门的最佳目标开度。同时,ECU采用H桥以占空比方式驱动节气门执行电动机,实现节气门的位置跟踪控制。
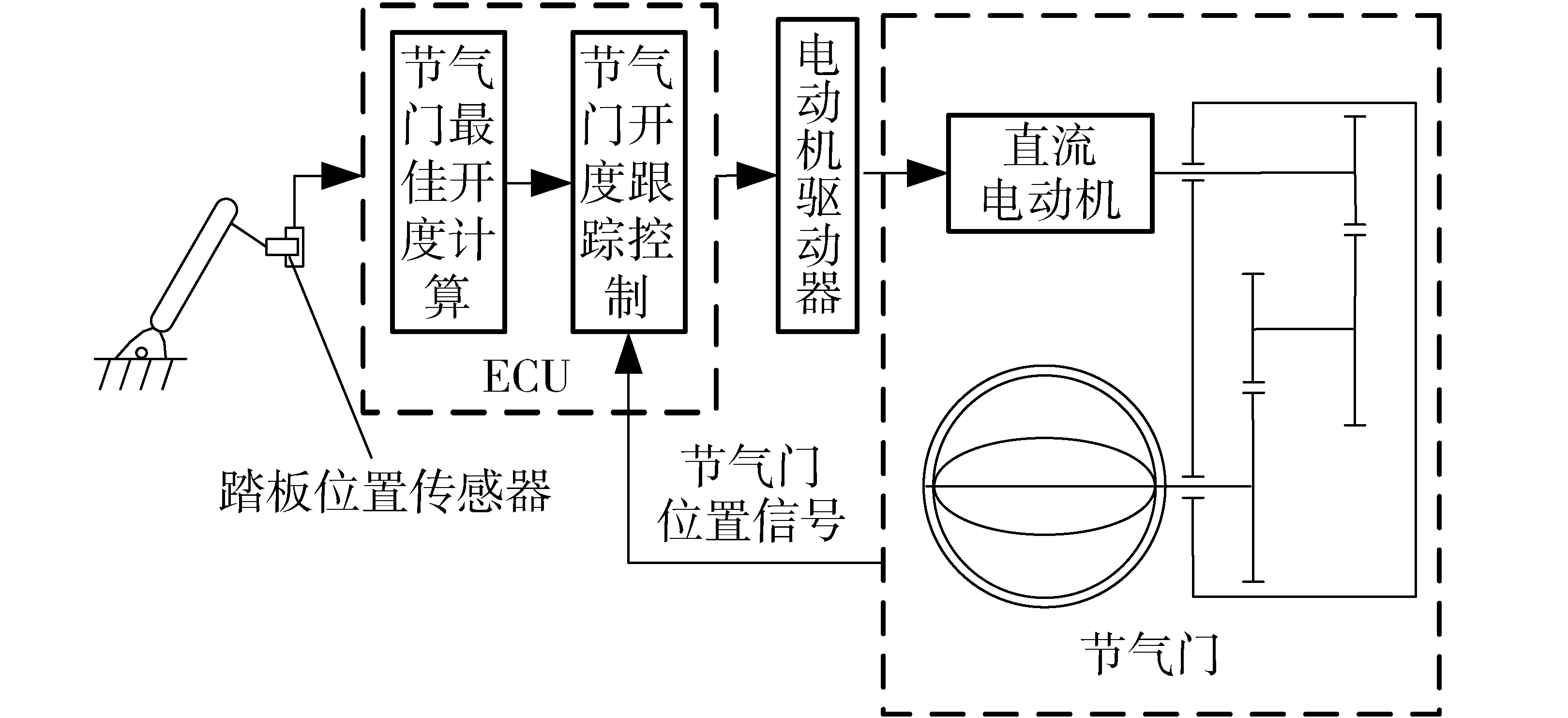
图1 电子节气门控制系统示意图Fig.1 Scheme of electronic throttle control system
采用额定电压为12 V的永磁有刷直流电动机作为节气门驱动电动机,电动机经由速比为20.68的两级齿轮机构驱动节气门阀片。节气门位置由安装在减速机构端的滑动电位计采集并发送到ECU中,形成位置闭环系统。
2 节气门状态空间模型
节气门工作原理如图2所示。节气门在运动过程中,会受到复位弹簧力矩、摩擦阻力以及进气气流等所产生的扰动力矩影响。
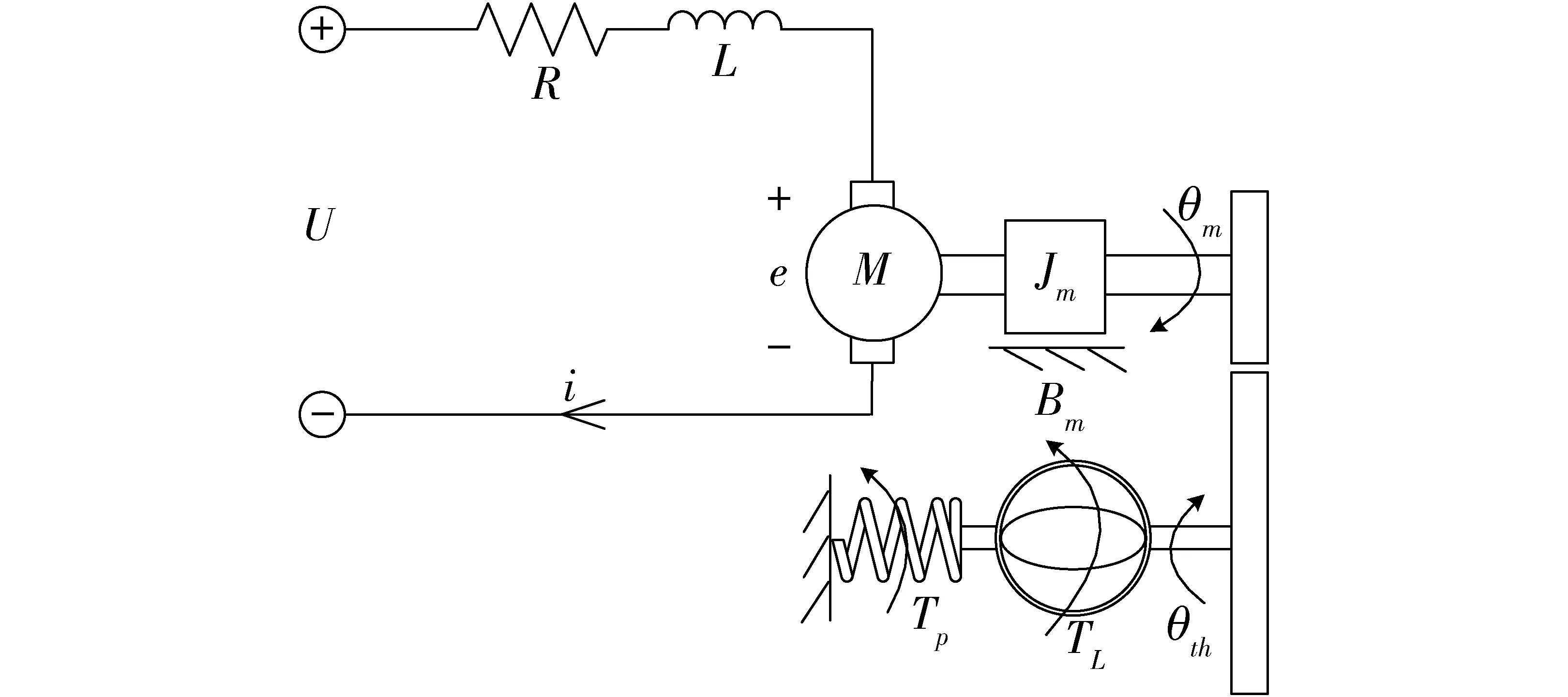
图2 电子节气门工作原理图Fig.2 Working principle diagram of ETC
根据牛顿第二定律和基尔霍夫定律,可得直流电动机的转矩和电压平衡方程[19]为
(1)
式中η——减速机构传动比kt——转矩常数i——电枢电流ke——反电动势常数R——电枢电阻ks——复位弹簧刚度L——电枢电感Jm——电动机转动惯量Jth——节气门转动惯量θth——节气门开度wm——电动机转速wth——节气门转速U——电动机输入电压Dm——电动机阻尼系数Dth——节气门阻尼系数Tp——预紧力矩TL——干扰力矩Jeq——折算到节气门轴处转动惯量Deq——折算到节气门轴处阻尼系数
由式(1)可得
(2)
定义节气门系统状态变量为
(3)
联立式(2)和式(3),可得电子节气门系统状态空间方程
Ax+Bu+Ew
(4)
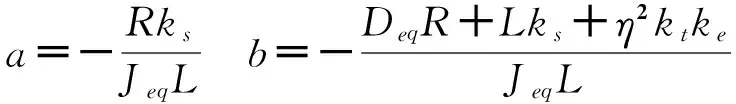
表1为ETCS的物理参数。将电子节气门状态空间方程按零阶保持器方法,以采样周期T=0.001 s进行离散,可得离散化的ETCS状态空间方程
(5)
其中
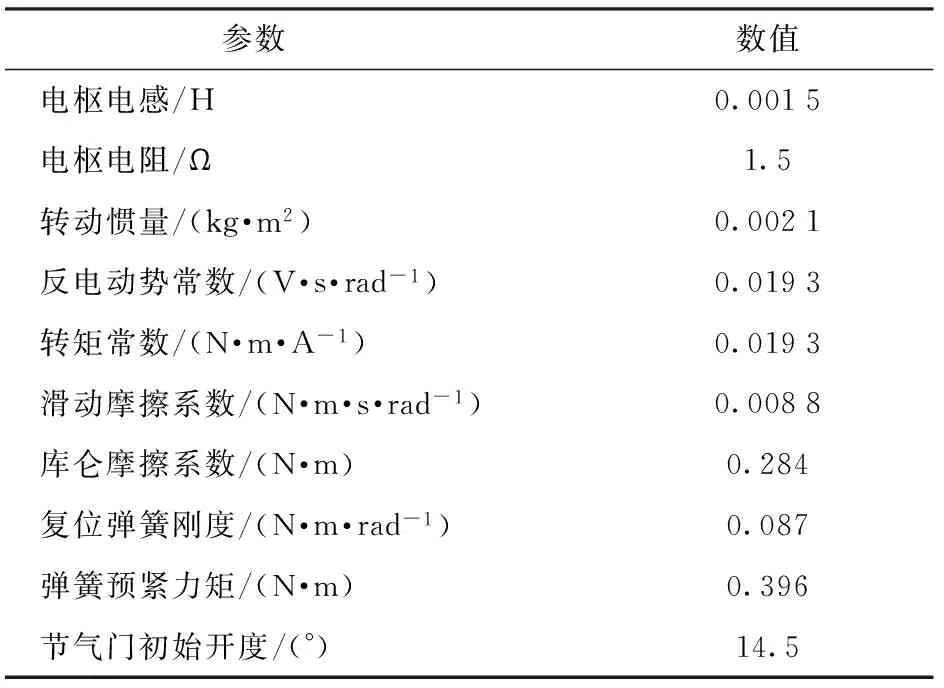
表1 电子节气门参数
3 最优预见控制器设计
3.1 扩大误差系统构造
定义预见控制器性能指标函数为
其中
e(k)=r(k)-y(k)
式中Qe——误差权重矩阵H——控制输入权重矩阵e(k)——跟踪误差信号r(k)——位置目标信号
由式(5)和式(6)可得
e(k+1)=r(k+1)-y(k+1)=r(k+1)-
Cdx(k+1)=r(k+1)-Cd(Adx(k)+
Bdu(k)+Edw(k))
(7)
引入位置目标信号信息,可得
xr(k+1)=Arxr(k)
(8)
其中
式中p——预见步长
若目标信号预见步长为p,即目标值信号r(k),r(k+1),r(k+2),…,r(k+p)均已知,并假设p步以后的目标信号为零,即
r(k+j)=0 (j=p+1,p+2,…)
为消除系统的稳态误差,引入离散积分器[20]
v(k+1)=v(k)+e(k)
(9)
其中v(0)可任意赋值,通常选取v(0)=0。
联立式(5)、(7)~(9),即得到扩大误差系统
(10)
其中
这样扩大误差系统中包含了预见目标信号,目标函数可以表示为
(11)
其中
Q=diag(Qe,Qv,0,0)
3.2 最优预见控制器设计
设计的最优预见控制器结构如图3所示,该控制器由预见、离散积分和反馈控制3部分组成。
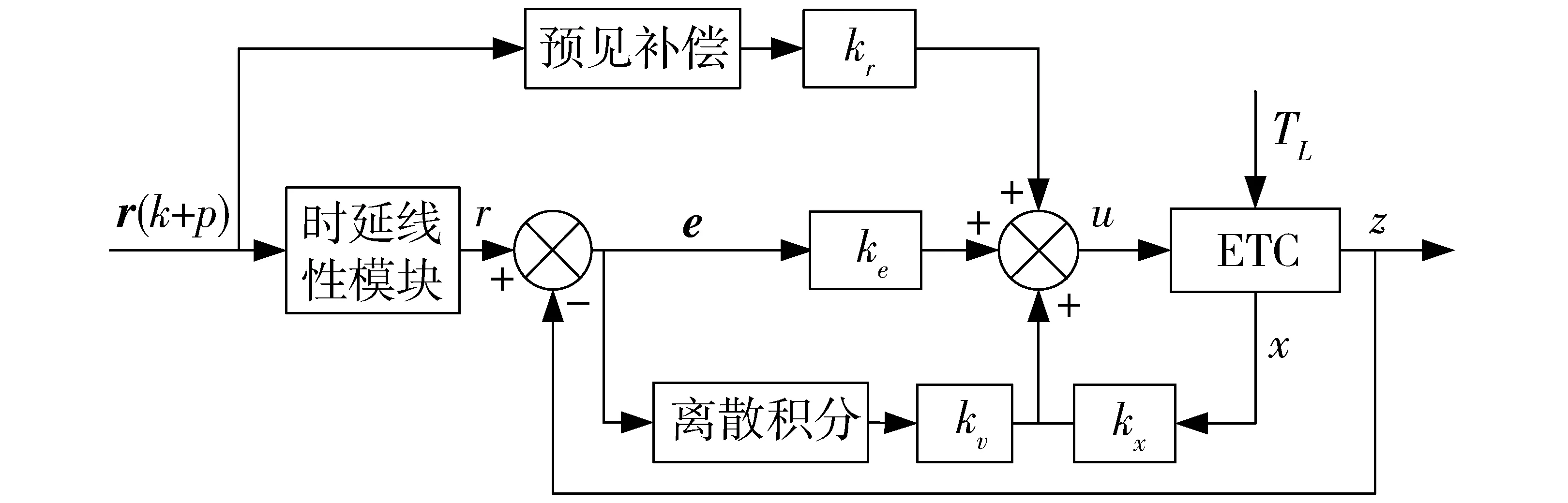
图3 离散最优预见控制器结构示意图Fig.3 Scheme of discrete optimal preview control
根据图3可得,系统的控制输入为
(12)
将式(12)代入式(10)中得
(13)
其中
定理1[21]:对于给定的正常数γ,以下条件等价。
(1)式(13)是渐进稳定的,且系统的H∞范数为
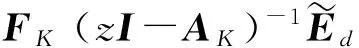
(2)存在一个对称矩阵X>0,使得
(14)
控制器为K=YX-1。
在线性矩阵不等式(14)的约束下对γ进行最小值搜索,可以得到一个具有线性矩阵不等式和线性目标函数的凸优化问题。
引理1:最小性能指标γ可以通过求解以下凸优化问题获得
(15)
4 节气门仿真结果分析
针对节气门执行机构进行仿真,并与传统PID控制进行比较,观察节气门在不同控制算法下的响应速度、超调量和鲁棒性等特性。选取加权矩阵Q=diag(10,5,0,0),R=1,选取预见步长p=2。所得系统静态控制增益为
K=[10.543 8 10.543 8 -607.422 5
-8.185 6 -0.008 0 0 10.543 9 10.544 0]
为充分验证最优预见控制算法的有效性,共进行以下5种情况的仿真分析:①ETCS为名义参数时,节气门由初始开度至大开度和大开度至小开度的连续阶跃响应如图4所示。②由于难以辨识ETCS的物理参数,为验证算法的鲁棒性,可在仿真中改变系统的物理参数。图5为参数翻倍时,节气门由初始开度至大开度和大开度至小开度的连续阶跃响应。③ETCS为名义参数时,节气门穿越初始开度的小幅度阶跃响应如图6所示。④ETCS为名义参数时,目标信号为穿越初始开度的小幅度阶跃信号,并且节气门阀片在4.6~5.4 s和6.6~7.4 s两个时间段受到大小为0.1 N·m的气流干扰力矩时的响应如图7所示。⑤ETCS为名义参数时,节气门阶梯阶跃响应如图8所示。
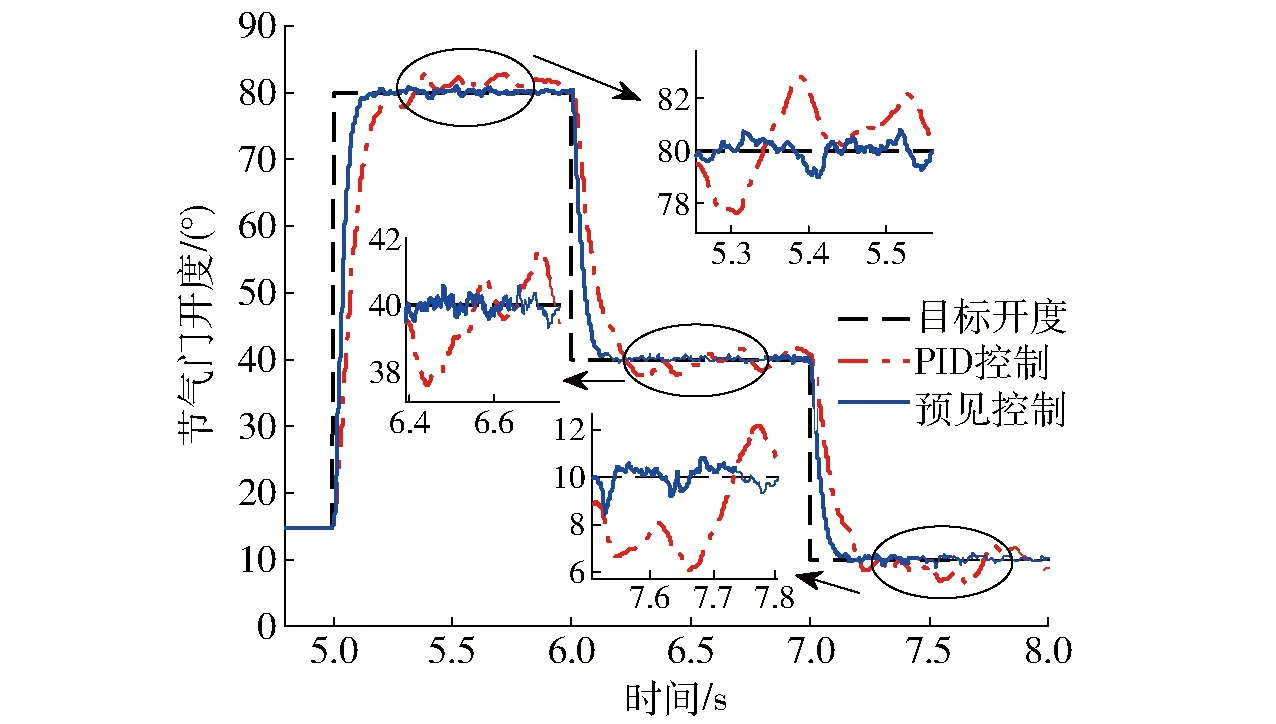
图4 名义模型参数仿真结果Fig.4 Simulation result for ETCS with nominal parameters
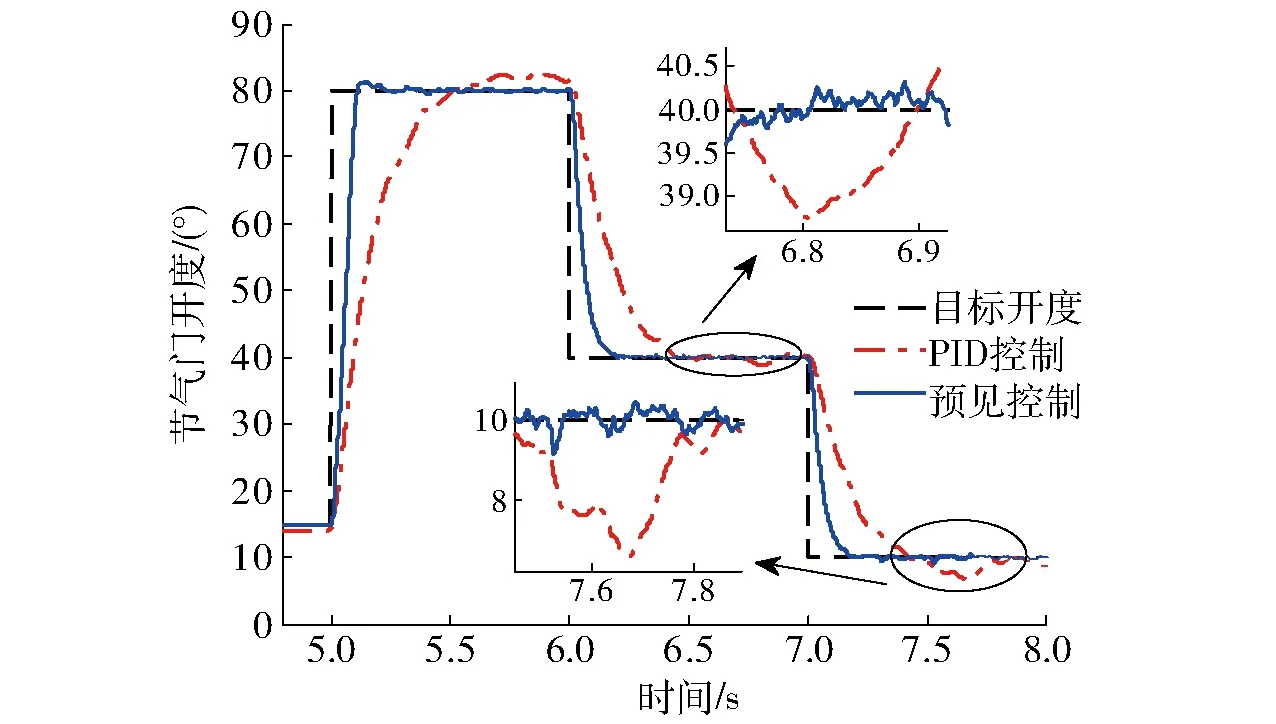
图5 ETCS参数翻倍时仿真结果Fig.5 Simulation result for ETCS with parameters doubled
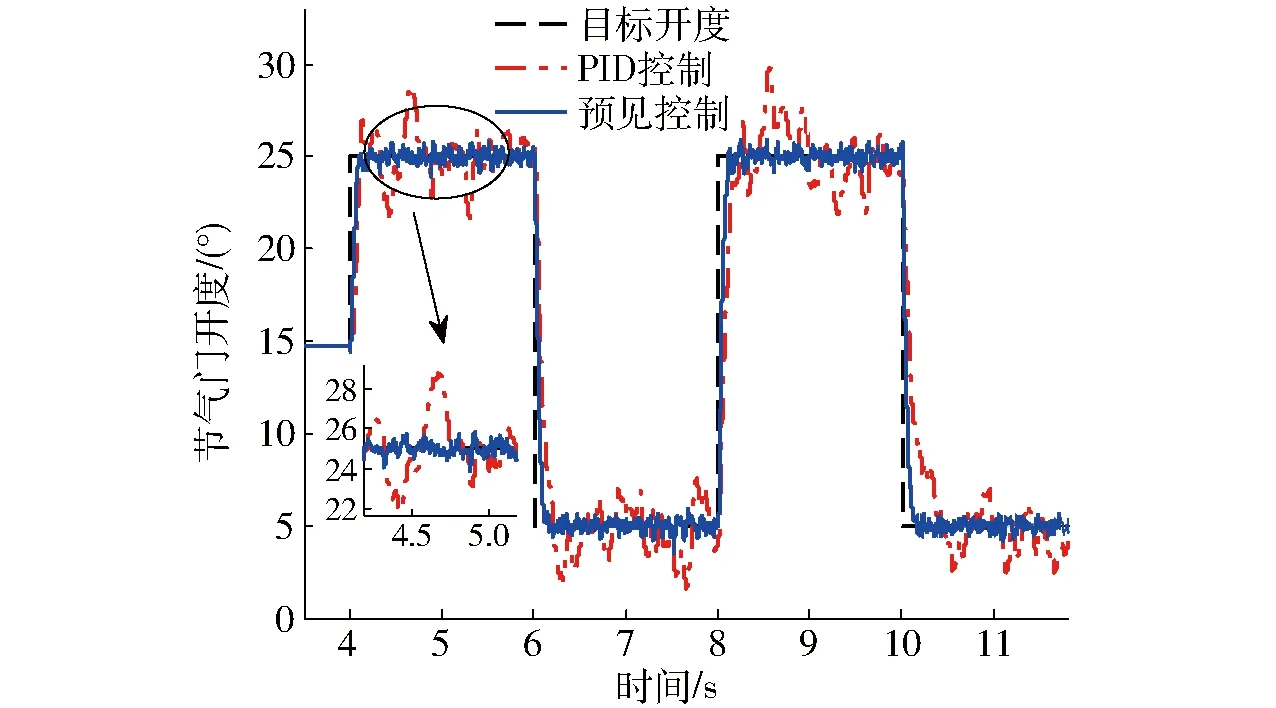
图6 节气门初始开度附近阶跃信号仿真结果Fig.6 Simulation result for ETCS near default position
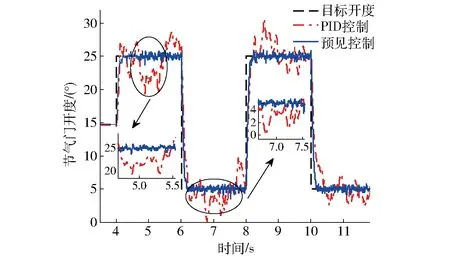
图7 节气门受到干扰力矩仿真结果Fig.7 Simulation result for ETCS with airflow disturbance
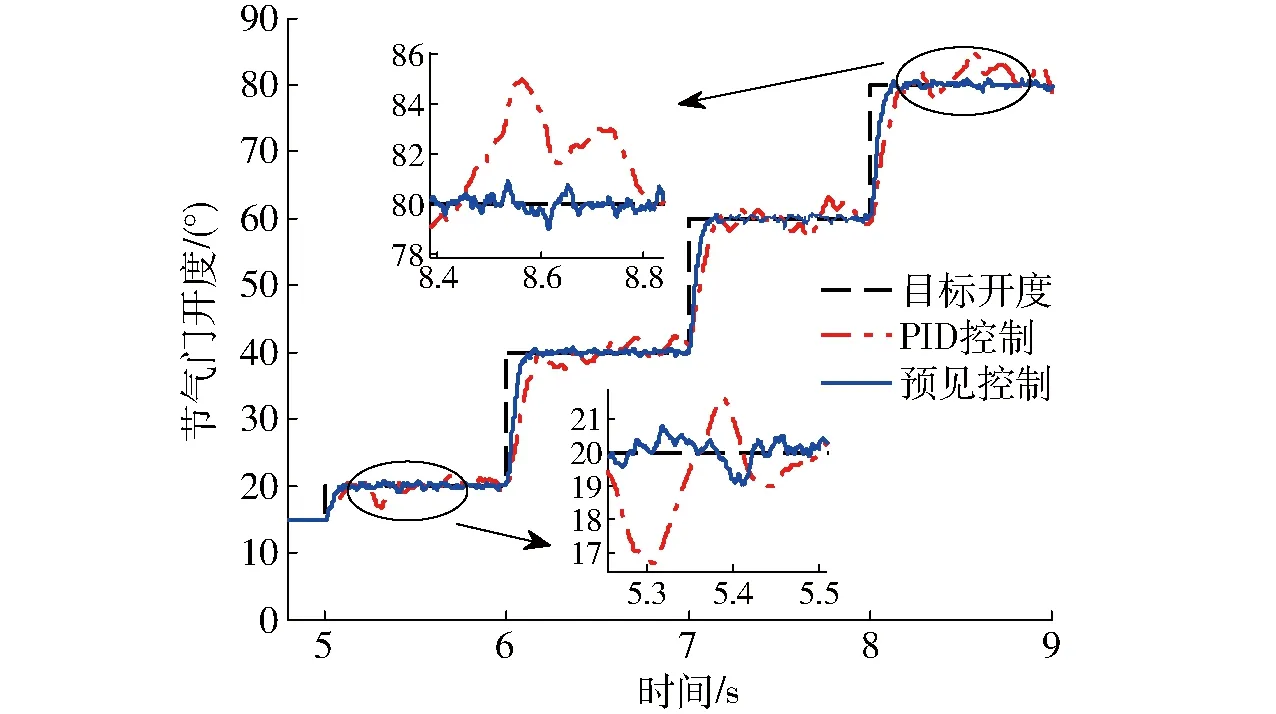
图8 节气门连续阶跃信号仿真结果Fig.8 Simulation result for ETCS under stair-step signal
由图4~8可知,采用最优预见控制算法的电子节气门控制系统响应速度较快,且无超调。而采用PID控制器时,为了满足一定的响应速度,会出现超调现象。对比图4和图5可知,当ETCS参数翻倍时,采用PID控制器的节气门响应时间明显变长,并且会出现较大的稳态误差。而采用最优预见算法的响应时间几乎不变,仅在节气门由初始开度至大开度阶跃时,出现小幅超调。由此说明,最优预见控制算法对模型参数的敏感性较低,鲁棒性能更强。图6和图7为节气门在初始开度附近的小幅度阶跃响应。由于系统的非线性等因素,传统PID控制的效果差,并且在受到外界干扰时,偏离预设值的幅度比较大,抗干扰能力较弱。
5 试验验证
基于Hilink控制器[22]搭建了以节气门为实物的快速控制原型试验模型,如图9所示,主要包括:上位机、节气门、节气门电动机驱动器以及Hilink控制器。

图9 电子节气门控制系统试验Fig.9 RCP platform for ETCS1.电子节气门 2.上位机 3.控制器 4.电动机驱动器
图10和图11分别为ETCS阶跃响应和正弦目标开度响应试验结果。由图可知,ETCS响应时间短,跟踪误差小,且在节气门开启和关闭时,均未出现较大超调。
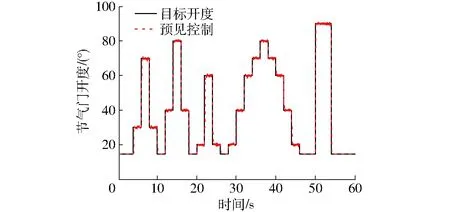
图10 节气门控制系统阶跃响应试验Fig.10 Tracking results of step response for ETCS
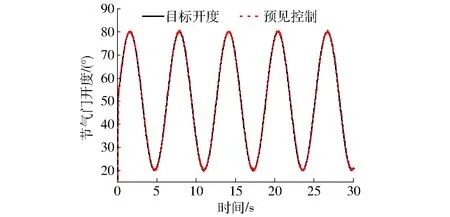
图11 节气门正弦目标开度响应试验Fig.11 Tracking results of sinusoidal position for ETCS
综上,仿真结果表明所设计的位置最优预见控制算法对系统参数敏感性低。试验结果也证实了所设计的控制器具有响应速度快、鲁棒性强的特点。
6 结束语
以电子节气门为控制对象,建立了包括永磁有刷直流电动机、复位弹簧和摩擦力矩的节气门状态空间模型,利用Matlab提供的连续系统离散化矩阵函数c2dm得到离散化的ETCS状态空间模型。采用状态转移法构建包含目标信号的扩大误差系统,避免对系统有关系数矩阵求差分,从而保证扩大误差系统结构简单。仿真和试验结果均表明,离散最优预见控制算法可以保证ETCS较快并准确地跟踪节气门目标开度,所设计的控制器对参数不确定性和外界干扰的敏感性降低,鲁棒性变强。对电子节气门进行离散最优预见控制,可以改善发动机性能,提高汽车的动力性和燃油经济性。
1 王斌,刘昭度,王仁广,等.汽车电子节气门模糊控制器快速控制原型设计[J].农业机械学报,2007,38(11):9-11. WANG Bin, LIU Zhaodu, WANG Renguang, et al. Design of rapid control prototyping for automotive electronic throttle fuzzy controller[J]. Transactions of the Chinese Society for Agricultral Machinery, 2007, 38(11): 9-11. (in Chinese)
2 陈宏羽.电子节气门控制系统开发及其算法研究[D].长春:吉林大学,2016. CHEN Hongyu. Development of electronic throttle control system and study on the control algorithm[D]. Changchun: Jilin University, 2016. (in Chinese)
3 QIAN Weikang, WANG Li, XIE Lingjun, et al. Practical solution for automotive electronic throttle control based on FPGA[C]∥2008 9th International Conference on Signal Processing, 2008: 453-457.
4 陈虹,宫洵,胡云峰,等. 汽车控制的研究现状与展望[J].自动化学报,2013,39(4):322-346. CHEN Hong, GONG Xun, HU Yunfeng, et al. Automotive control: the state of the art and perspective[J]. Acta Automatica Sinica, 2013, 39(4): 322-346. (in Chinese)
5 王耀南,申永鹏,孟步敏,等.车用汽油发动机电子控制系统研究现状与展望[J].控制理论与应用,2015,32(4):432-447. WANG Yaonan, SHEN Yongpeng, MENG Bumin, et al. Electronic control system for gasoline automotive engine: state of the art and perspective[J]. Journal of Control Theory and Applications, 2015, 32(4): 432-447. (in Chinese)
6 巩明德,田博,王辉.基于双向伺服力反馈的电子节气门控制系统[J/OL].农业机械学报,2013,44(5):1-6,24.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130501&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2013.05.001. GONG Mingde, TIAN Bo, WANG Hui. Electronic throttle control system based on bilateral servo with force feedback[J/OL]. Transactions of the Chinese Society for Agricultral Machinery, 2013, 44(5): 1-6,24. (in Chinese)
7 陈虹,胡云峰,郭宏志,等.基于backstepping方法的电子节气门控制[J].控制理论与应用,2011,28(4):491-496. CHEN Hong, HU Yunfeng, GUO Hongzhi, et al. Control of electronic throttle based on backstepping approach[J]. Journal of Control Theory and Applications, 2011, 28(4):491-496. (in Chinese)
8 JIAO X, ZHANG J, SHEN T. An adaptive servo control strategy for automotive electronic throttle and experimental validation[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6275-6284.
9 BAI R, LIU Y, WANG S. Fuzzy sliding-mode control of the electronic throttle system[C]∥2014 11th World Congress on Intelligent Control and Automation (WCICA), 2014: 747-750.
10 GREPL R, LEE B. Modeling, parameter estimation and nonlinear control of automotive electronic throttle using a rapid-control prototyping technique[J]. International Journal of Automotive Technology, 2010, 11(4): 601-610.
11 VASAK Mario, BAOTIC Mato, PETROVIC Ivan, et al. Hybrid theory-based time-optimal control of an electronic throttle[J]. IEEE Transactions on Industrial Electronics, 2007, 54(3): 1483-1494.
12 甄子洋.预见控制理论及应用研究进展[J].自动化学报,2016(2):172-188. ZHEN Ziyang. Research development in preview control theory and applications[J]. Acta Automatica Sinica, 2016(2): 172-188. (in Chinese)
13 HAZELL A. Discrete-time optimal preview control[D]. London: University of London, 2008.
14 朱浩,刘少军,邱显焱.车辆主动悬挂最优预见控制模型[J].交通运输工程学报,2005,5(3):8-13. ZHU Hao, LIU Shaojun, QIU Xianyan. Optimum-preview control model of rail vehicle active suspension[J]. Journal of Transportation Engineering, 2005, 5(3): 8-13. (in Chinese)
15 PRABAKAR R S, SUJATHA C, NARAYANAN S. Optimal semi-active preview control response of a half car vehicle model with magnetorheological damper[J]. Journal of Sound and Vibration, 2009, 326(3): 400-420.
16 SALEH L, CHEVREL P, CLAVEAU F, et al. Shared steering control between a driver and an automation: stability in the presence of driver behavior uncertainty[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 974-983.
17 MIANZO L, PENG H. Output feedback preview control of an electromechanical valve actuator[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 428-437.
18 ZHANG C, VAHIDI A. Route preview in energy management of plug-in hybrid vehicles[J]. IEEE Transactions on Control Systems Technology, 2012, 20(2): 546-553.
19 LOH R N K, PORNTHANOMWONG T, PYKO J S, et al. Modeling, parameters identification, and control of an electronic throttle control (ETC) system[C]∥ICIAS 2007 International Conference on Intelligent and Advanced Systems, 2007: 1029-1035.
20 LIAO F, TAKABA K, KATAYAMA T, et al. Design of an optimal preview servomechanism for discrete-time systems in a multirate setting[J]. Dynamics of Continuous Discrete and Impulsive Systems Series B, 2003, 10: 727-744.
21 俞立.鲁棒控制:线性矩阵不等式处理方法[M]. 北京:清华大学出版社,2002.
22 Real-time hardware-in-the-loop control platform for Matlab/Simulink/datasheet[OL]. Available: http:∥zeltom.com/products/hilink.
Optimal Preview Position Control for Automotive Electronic Throttle
ZHANG Bangji1CHEN Zhiqiang1TIAN Yang2ZHANG Nong3WANG Ming1
(1.StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,HunanUniversity,Changsha410082,China2.FacultyofEngineeringandInformationTechnology,UniversityofTechnologySydney,SydneyNSW2007,Australia3.SchoolofAutomotiveandTrafficEngineering,HefeiUniversityofTechnology,Hefei230009,China)
Based on the theories of linear quadratic regulator (LQR) control and linear matrix inequality (LMI), a scheme of discrete-time optimal preview position control algorithm for automotive electronic throttle control (ETC) system was proposed. The presented throttle valve position tracking control algorithm consisted of the state-feedback control, discrete integrator, and preview feed-forward control. The closed-loop controller was realized by only utilizing a low-cost sliding potentiometer which was used to measure the angle position of the throttle valve. To track the position of automotive electronic throttle valve, the discrete-time state space model was firstly established for the automotive ETC system. Then, the augmented error system which contained future position reference information was built by using the state transformation method instead of the traditional difference method, which helped to simplify the structure of the augmented error system. In simulations, the physical parameters uncertainty and external disturbance torque of the real automotive electronic throttle control system were also considered, and the simulation results were verified by bench tests for throttle through utilization of the rapid control prototyping (RCP) technology. Both simulation and test results demonstrated that the proposed discrete-time optimal preview position control algorithm was able to effectively improve the transient performance and robustness of the ETC system while guaranteeing the tracking accuracy. Hence, the application of the presented control scheme on the ETC system can further improve the fuel economy, dynamic and exhaust performance of gasoline engine.
automotive electronic throttle; position tracking; optimal preview control; rapid control prototyping; robustness
10.6041/j.issn.1000-1298.2017.04.046
2016-12-01
2016-12-28
国家自然科学基金项目(U1234208)和汽车车身先进设计制造国家重点实验室自主项目(71575005)
张邦基(1967—),男,教授,主要从事车辆传动系统控制技术和NVH研究,E-mail: bangjizhang@hnu.edu.cn
U464.134+.3
A
1000-1298(2017)04-0349-06

