不凝性气体及湍流扰动对喷嘴孔内空化现象的影响

麻 斌 高 莹 刘 宇 刘洪岐 陈 伟 徐英健

(吉林大学汽车仿真与控制国家重点实验室, 长春 130025)

不凝性气体及湍流扰动对喷嘴孔内空化现象的影响

麻 斌 高 莹 刘 宇 刘洪岐 陈 伟 徐英健

(吉林大学汽车仿真与控制国家重点实验室, 长春 130025)

利用ANSYS_Fluent 15.0软件，在两相流计算采用均相流模型(HEM)、湍流计算采用realizablek-ε模型基础上，分别基于SS及Singhal空化模型对喷嘴孔内空化现象进行数值模拟，并将模拟结果与试验结果进行对比分析，其中前者忽略了不凝性气体及湍流扰动对孔内空化现象的影响，而后者考虑了这2个因素。其后在两相流计算仍然采用均相流模型的基础上，将Singhal空化模型与不同的湍流模型组合应用，并与试验结果进行对比分析。结果显示：不凝性气体及湍流扰动对喷嘴孔内空化现象数值模拟存在显著影响，不考虑这2个因素时计算所得喷孔内气相区域分布规律与试验结果一致，然而计算所得气相体积分数仅为试验结果的42%，考虑这2个因素时计算所得气相区域分布规律同样与试验结果一致，且计算所得气相体积分数约为试验结果的96%，即考虑不凝性气体及湍流扰动的影响会使喷嘴孔内空化现象数值模拟更加准确；考虑不凝性气体及湍流扰动时计算所得气相区域在其末端出现小幅扩散现象，这种扩散现象源于不凝性气体在气相区域末端的膨胀作用；湍流粘度的计算结果通过影响场内流速、静压的方式最终对计算所得喷孔内气相区域分布产生一定影响。

喷嘴； 空化； 数值模拟； 不凝性气体； 湍流扰动

引言

喷嘴孔内空化现象指高压燃油由于流道转折、流通截面突缩等原因导致流速急剧升高，静压下降至其饱和蒸汽压以下并发生汽化，从而在喷孔内出现由燃油蒸汽及部分不凝性气体(Noncondensable gases,NCG)与液态燃油构成的气液两相流现象。喷嘴孔内空化现象对燃油喷雾特性有显著影响，进而影响缸内燃油喷射发动机的排放性能和燃油经济性[1-2]，适当强度的空化现象可以大幅提升喷雾锥角，而过度的空化现象又会使喷雾锥角急剧降低[3-4]。为了降低发动机排放并提高燃油经济性，现代柴油机及GDI汽油机均采用高压喷射的策略以优化喷雾质量，在这种情况下喷油器喷孔内不可避免地出现空化现象，因此国内外学者对喷嘴孔内空化现象进行了大量的试验研究及数值模拟分析，以掌握空化的发生、发展、溃灭等机制，分析其影响因素，实现对燃油喷射过程更全面的控制，从而改善发动机性能。

由于在实际尺寸及实际几何形状的喷嘴中进行可视化试验十分困难，因此大量有关喷嘴孔内空化现象的试验是基于比例放大且简化几何形状的喷嘴进行的，值得注意的是，为使基于放大喷嘴的可视化试验结果能够应用于实际尺寸喷嘴，试验时需要保证放大喷嘴与实际喷嘴内雷诺数及空化数这2个无量纲数的一致相似性[1-14]。

在比例放大喷嘴中进行的可视化试验虽然可以得到许多有关空化现象的重要结论，但仍有一些问题无法完全依靠这种方法来进行研究，如喷嘴尺寸变化会对喷孔内空化现象造成何种影响、实际喷嘴较为复杂的几何形状会对喷孔内空化现象造成何种影响等，准确的数值模拟计算为研究这些问题提供了一种有效的研究手段[15-19]。

对喷嘴孔内空化现象进行模拟计算，主要涉及的计算模型有空化模型、湍流模型及多相流模型，目前应用较多的空化模型出于简化计算模型的考虑，在计算过程中忽略了不凝性气体及湍流扰动(Turbulent pressure fluctuations,TPF)的影响，如SS模型(Schnerr and Sauer Model)、ZGB(Zwart Gerber Belamri)模型、Kunz 模型等。然而，不凝性气体的存在不仅会影响液相中的初始气核数，且会在低压区因为膨胀作用体积急剧增大，从而与空化效应产生的蒸汽共同组成空化两相流中的气相；湍流扰动则会使液相饱和蒸汽压上升[20]，即改变空化现象发生的临界条件。本文应用Fluent 15.0软件，在多相流计算均使用均相流模型的基础上，分别建立基于SS空化模型的模型1及基于Singhal空化模型的模型2，并将数值计算结果与文献[6]中试验结果进行对比分析，其中模型1忽略不凝性气体及湍流扰动的影响，而模型2则考虑不凝性气体及湍流扰动的影响。最后，对Singhal空化模型与不同湍流模型配合的应用效果进行对比分析。

1 数学模型及计算设置

1.1 模型1

模型1采用均相流计算模型，假设液相与气相在流场内各点均充分混合，且忽略了液相与气相之间相间滑移(Slip velocity)的影响，直接对混合相进行输运方程求解。另外由于空化现象主要受流场内压力变化的影响，且在模拟计算中不考虑流体可压缩性，故无需进行能量方程的求解，只需对液相与蒸汽相构成的混合相进行连续方程及动量方程求解。混合相连续方程及动量方程如下

(1)

(2)

式中vm——混合相流速ρm——混合相密度P——压力μm——混合相动力粘度

由于不考虑液相中不凝性气体的影响，即气相只含蒸汽组分，有

ρm=αvρv+αlρl

(3)

μm=αvμv+αlμl

(4)

式中ρv——蒸汽相密度ρl——液相密度μv——蒸汽相动力粘度μl——液相动力粘度αv——蒸汽相体积分数αl——液相体积分数

联立方程(1)～(4)，注意到混合相输运方程与单相输运方程相比多出一个未知数，即蒸汽相体积分数αv，该未知数可通过对气相连续方程(5)进行求解，并配以SS空化模型(6)来得到。计算公式为

(5)

其中

(6)

式中R——液相至蒸汽相质量转换率r——蒸汽相气泡半径

通常在进行空化现象模拟计算时，均假设蒸汽相气泡是由液相中存在的初始气核成长而来，于是空化现象的增强与减弱过程可以转换为初始气核的增大与减小过程，而目前应用最广泛的用以描述气核成长的气泡动力学方程为Rayleigh-Plesset方程[21]。在SS空化模型中对该方程进行简化，忽略其中的高阶项、表面张力项、粘性力项等，只保留低阶项及瞬时张力项，于是有

(7)

式中psat——饱和蒸汽压p——流场静压

联立方程(6)及方程(7),得蒸汽相气泡成长及破碎方程为

(8)

其中

(9)

可得

(10)

式中n——空化初始气核数密度

理论上n可以通过求解其输运方程的方式来确定，但这会带来过高的计算成本，此处选为定值1013[2,22]。

通过联立方程(5)、方程(8)及方程(10)，即可完成对蒸汽相体积分数的求解，从而使整个计算方程组封闭。

1.2 模型2

模型2同样采用均相流模型，直接对混合相进行输运方程求解，另外虽然考虑了不凝性气体的可压缩性，但只是将其定义为压力场的单值函数，故仍然无需求解能量方程。混合相连续方程及动量方程计算同模型1，仍然采用式(1)及式(2)，不同之处在于：由于模型2的气相由蒸汽及不凝性气体2种组分构成，故混合相密度及粘度计算公式为

ρm=αvρv+αlρl+αnρn

(11)

μm=αvμv+αlμl+αnμn

(12)

式中ρn——不凝性气体密度μn——不凝性气体动力粘度αn——不凝性气体体积分数

不凝性气体体积分数αn在计算中作为边界条件直接给出，随液相一起进入流场；蒸汽相体积分数αv的计算同模型1，即通过对气相连续方程进行求解，并配以空化模型来得到。不同之处在于模型2采用Singhal空化模型来计算液相至蒸汽相的质量转化率，Singhal空化模型提供的蒸汽相气泡成长及破碎方程与SS空化模型相比有两点不同。首先，Singhal空化模型对气泡直径r的计算不是由空化初始气核数密度n及蒸汽相体积分数αv计算得来，而是通过气动阻力及表面张力的平衡方程进行计算；其次，Singhal空化模型基于湍流扰动对液相饱和蒸汽压进行修正。最终蒸汽相气泡成长及破碎方程为

(13)

其中

p′sat=psat+0.195ρmk

(14)

式中p′sat——修正后的饱和蒸汽压k——湍动能σ——表面张力系数

通过联立方程(5)、方程(13)及方程(14)，即可完成对蒸汽相体积分数的求解，从而使整个计算方程组封闭。

1.3 湍流模型

本文所采用湍流模型为工业设计中应用比较广泛的realizablek-ε、SSTk-ω和RSM(Reynolds stress model)3种湍流模型。其中，前两者属于雷诺平均模型，且分别属于k-ε系列湍流模型及k-ω系列湍流模型中应用效果较佳的模型，它们分别求解湍动能k、湍流耗散率ε及比耗散率ω的输运方程，而后利用k、ε、ω的值求解湍流粘度，最终求得动量方程中出现的雷诺应力，从而使整个方程组封闭。RSM湍流模型则直接求解雷诺应力的输运方程，计算量略大于雷诺平均模型，但在某些情况下计算精度高于雷诺平均模型。

1.4 网格及计算设置

采用文献[6]中的试验数据与模拟计算结果进行对比分析，因此所制作网格文件的整体几何形状与文献[6]中试验喷嘴的流域相同，其喷孔长度为16 mm，宽度为4 mm，厚度为1 mm。

本文采用试验数据中喷孔尺寸较实际喷油器喷孔尺寸(通常在0.2 mm左右)大，这是基于两方面的考虑：首先，在实际尺寸及实际几何形状的喷嘴中进行可视化试验十分困难，若喷嘴材质采用金属，则只能应用X光透视技术进行可视化试验[23]，所得试验图像十分模糊，参考价值有限，若喷嘴材质采用聚丙烯酸酯胶片等透明材质，则在试验中喷嘴又很容易被高压入流冲毁,导致可用试验结果十分有限[9]；其次，相关研究表明，在保证放大尺寸喷嘴及实际尺寸喷嘴中雷诺数及空化数这2个无量纲数相同的前提下，2种喷嘴中出现的空化两相流分布形态基本相同，即在保证雷诺数及空化数一致的前提下，采用放大尺寸喷嘴进行可视化试验获得的结论可近似应用于实际喷嘴[1-2,8]。

由于网格质量对CFD计算结果的影响十分显著，本文选择了一系列不同密度的网格进行计算以验证网格无关性，最终确定适用于本文研究内容的网格文件如图1所示[6]，为清晰反映网格局部加密情况，只给出了XY平面的视图。该网格为三维纯六面体网格，在流域入口、喷孔及喷孔入口、流域近壁面等处均进行了网格加密，喷孔处六面体数目约为322 000，喷孔上游处六面体数目约为503 000，喷孔及喷孔入口处网格最小尺寸为17 μm×40 μm×100 μm(分布于近壁面附近)，最大尺寸为40 μm×40 μm×100 μm(分布于喷孔轴线附近)。

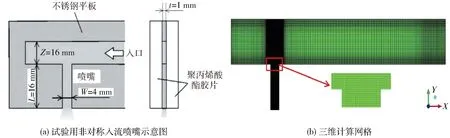
图1 喷嘴几何形状及三维计算网格Fig.1 Structure of test nozzle and 3D computational grid

在模拟计算中入口边界条件采用速度入口，流速由文献[6]中的试验条件确定，出口边界条件采用压力出口，并将其设置为0.1 MPa；计算用工质采用同试验一致的水及水蒸气，其物性参数如表1所示；计算服务器主要配置为：2个英特尔E5-2650 V3 @2.30 GHz×10处理器，25 M缓存。计算步长为0.1 ms，模型1大约2 d可完成一次计算，模型2大约2.5 d可完成一次计算。

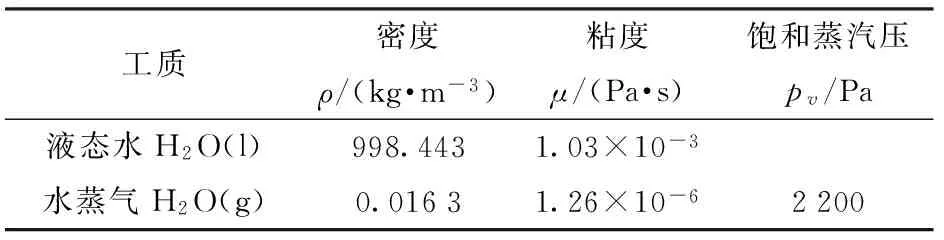
表1 工质物性参数

2 数值计算及结果分析

2.1 不凝性气体及湍流扰动的影响

首先对喷孔内超空化现象进行模拟计算，在完成计算影响因素分析及与试验数据的对比之后，再将所得模型应用于空化初生、发展空化等其他空化流动状态[1]。

通过对文献[6]提供数据的整理和计算，获得非对称入流喷嘴内超空化现象对应边界条件如表2所示。

模型2中不凝性气体质量分数也作为边界条件给出，在流场入口处随液相一起进入，其计算过程如下：

表2 边界条件(超空化现象)

水中不凝性气体主要来源有两方面，一方面为水中本身溶解的空气，另一方面则是水在试验过程中达到低压状态时，由环境漏入试验设备的空气，该部分空气不溶于水，而是在试验设备中与水共存。假设文献[6]在进行试验时，其试验设备密封性良好，且只考虑空气中的N2与O2。文献[6]中试验所采用水中氧气质量浓度为9 mg/L，又由亨利定律知，N2在水中溶解体积分数与O2在水中溶解体积分数之比为4.40/8.68，于是可得水中不凝性气体质量浓度为

fNCG=fO2+fN2=

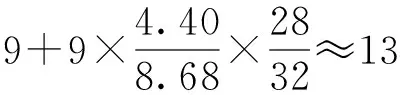
(15)

在计算过程中，喷嘴进出口质量流量差在10 ms左右趋于稳定，如图2所示为模型1计算所得喷嘴进出口质量流量差，因此将计算时间总长定为15 ms，并在与试验结果进行对比分析时采用15 ms时的计算结果。

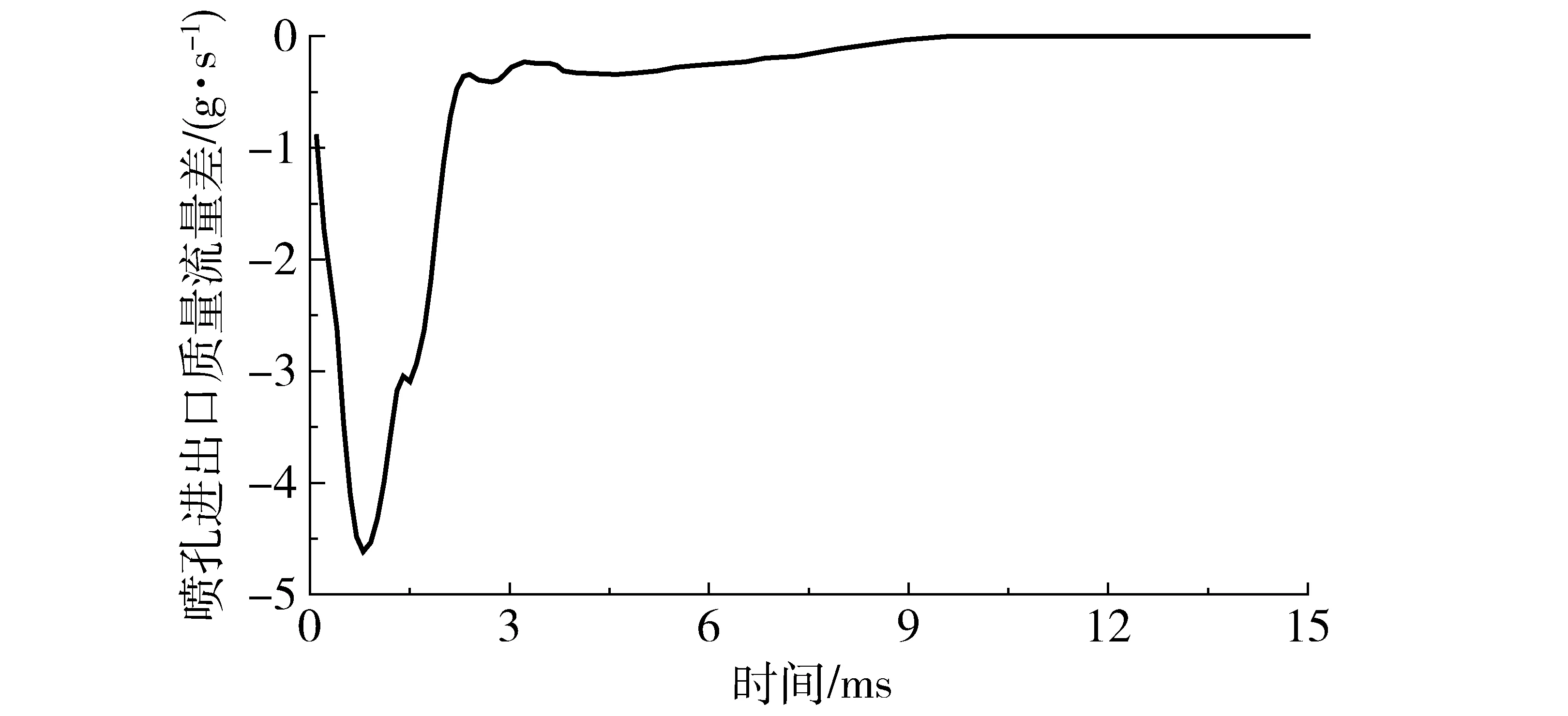
图2 进出口质量流量差Fig.2 Difference of mass flow rate for inflow and outflow

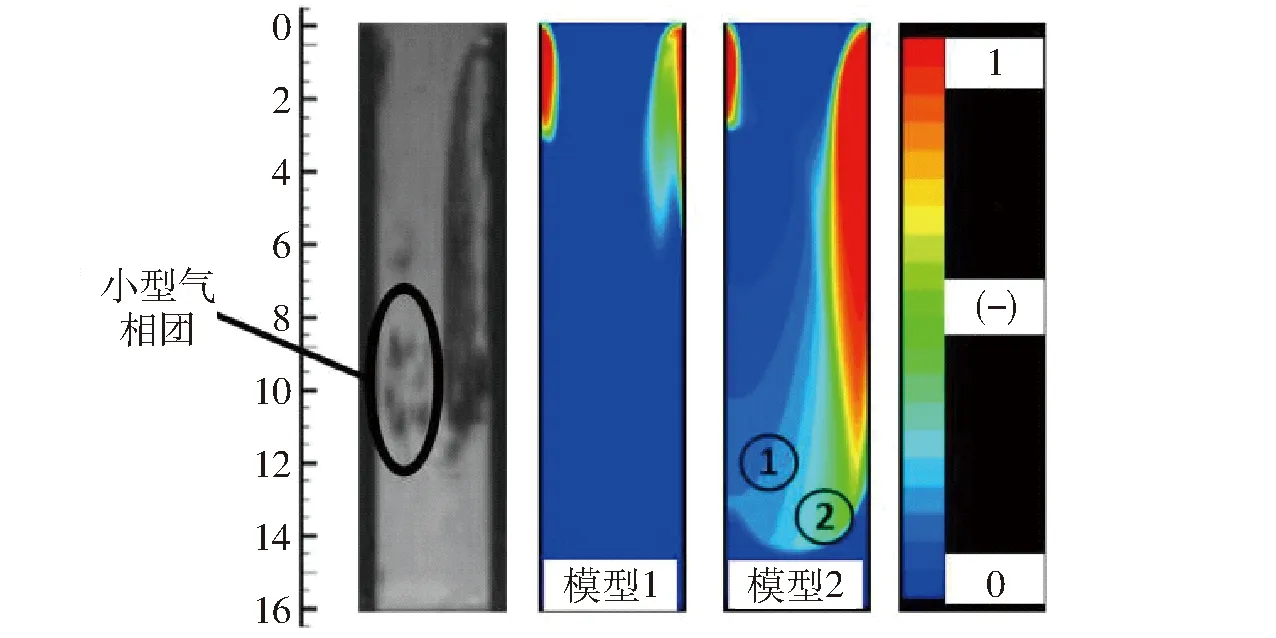
图3 喷孔内气相区域计算云图与试验结果对比Fig.3 Comparison between simulation and experiment results of gas phase region in nozzle

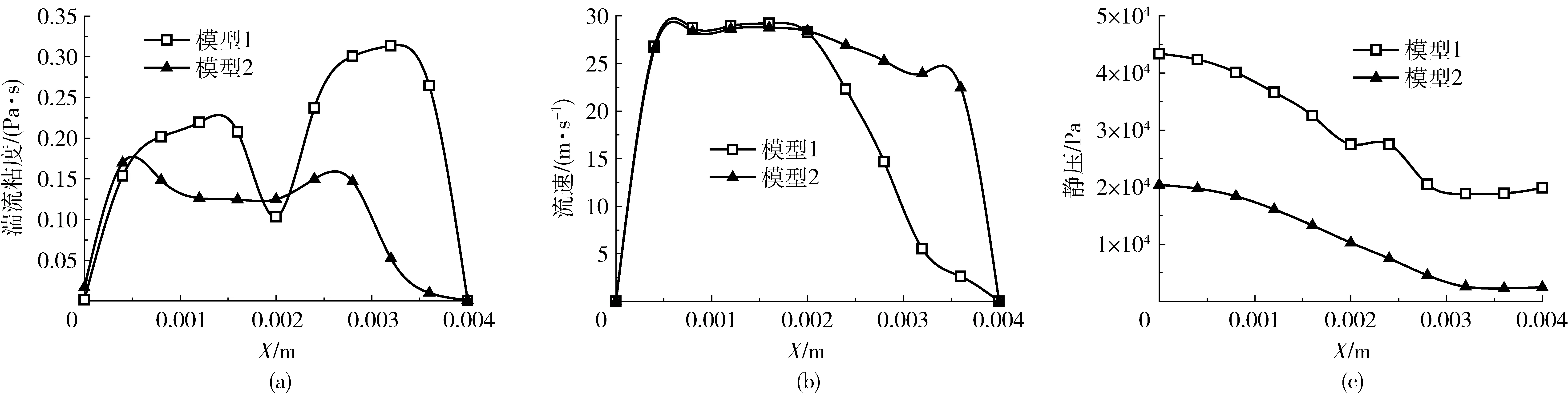
图5 喷孔在长度8 mm处截面上的湍流粘度、流速及静压计算结果Fig.5 Turbulence viscosity, velocity and static pressure at nozzle length of 8 mm

图3所示为在湍流模型均采用realizablek-ε的前提下，模型1与模型2计算所得喷嘴孔内气相区域分布与试验结果[6]的对比情况，需要指出的是，本文所示云图均来自喷嘴厚度为0.5 mm处的剖面。可以看到：模型1及模型2计算所得气化区域均呈左短右长的分布状态，这与试验结果保持一致；模型1计算所得右侧气相区域长度明显小于试验观测值(仅为试验观测值的42%)；模型2计算所得右侧气相区域长度与试验观测值较为接近(约为试验观测值的96%)，同时在气化区域末端位置存在一定程度的扩散现象，其扩散方向为由近壁面向轴线方向扩散；总体而言，模型2计算结果在气化区域分布状态及气化区域长度两方面均与试验结果吻合较为良好，即考虑不凝性气体及湍流扰动的模型计算结果与试验结果更加吻合；试验中观测到有小型气相团从气化区域中分离出去，而模型1及模型2均未能捕捉到这一现象。

在模型2计算所得气相区域的发散部分选取了a、b两点，分别计算其修正后的饱和蒸汽压p′sat，并与该点处的流场静压p进行对比，其结果如图4所示。分析可知，首先流场静压p在点a及点b处均大于经过修正后的饱和蒸汽压p′sat，即在这两点及其周边区域并无液相至气相的相变过程发生；其次流场静压p在点a及点b处均远小于大气压力，分别是大气压力的8.8%及4.7%，即不凝性气体所受液流压力仅为大气压力的8.8%及4.7%，故将在这两点及其周边区域发生急剧的膨胀。因此可以认为模型2计算所得气相区域在末端发生扩散是由不凝性气体在该区域的膨胀作用引发的。

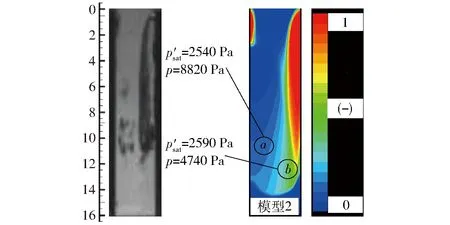
图4 模型2气相区域末端饱和蒸汽压修正Fig.4 Correction of saturated vapor pressure in model 2

图5所示为在喷孔长度为8 mm截面处模型1及模型2计算所得喷嘴孔内混合相湍流粘度、流速及流场静压的变化曲线。

可以看到，与模型1计算结果相比，模型2计算所得混合相湍流粘度在右侧壁面附近较小(图5a)，导致混合相流速在右侧壁面附近较大(图5b)，并进一步使得混合相静压在全流域内均明显小于模型1计算结果(图5c)，最终导致模型2计算所得气相体积分数显著大于模型1计算结果。然而需要注意的是，模型2计算所得气相体积分数大于模型1计算结果，这不仅仅因为湍流粘度的计算结果不同导致，更重要的是源于模型2对不凝性气体及湍流扰动的考虑：首先，模型1计算所得气相区域均来源于压降诱发的空化效应，而模型2计算所得气相区域不仅来源于空化效应，同时也来源于不凝性气体在低压区域的膨胀作用，因此会使计算所得气相区域增多；其次，模型2依据湍流扰动对饱和蒸汽压进行修正，使其升高，即提高了空化效应发生的临界压力，从而加剧空化效应，使计算所得气相区域增多。

2.2 湍流粘度的影响

在喷嘴孔内空化现象数值模拟过程中，对流场内压力的计算精度要求十分苛刻，这是由于流体液态至气态的相变过程由压降诱发，而发生相变的压力临界值只有2 000～4 000 Pa，与大气压相比只有其2%～4%，因此些许误差就会使最终的计算结果偏离试验结果。而流场内尤其是近壁处的湍流粘度会对压力场的准确计算造成很大影响，同时湍动能对模型2中饱和蒸汽压修正方程(14)的计算结果有很大影响，因此有必要对模型2与不同湍流模型配合使用时的应用效果进行研究分析。

图6所示分别为模型2与realizablek-ε、SSTk-ω及RSM湍流模型配合计算所得喷嘴孔内气相区域分布与试验结果[6]的对比情况。可以看到：模型2配合3种湍流模型计算所得气相区域均符合左长右短的分布规律，但也均存在气相区域分布扩散的情况；采用SSTk-ω湍流模型进行计算时，气相区域在左侧较短、在右侧由壁面向喷孔轴线方向扩散较为严重；采用RSM湍流模型进行计算时，气相区域在左侧较长、在右侧沿液流方向扩散较为严重；采用SSTk-ω或RSM湍流模型的计算结果均没有采用realizablek-ε湍流模型计算所得气相区域更加贴近试验结果，另外3个计算结果均未能捕捉到试验中出现的微小气相团。

图6中标注的点1、点2、点3处计算所得湍流粘度、修正后饱和蒸汽压及流场静压如表3所示。

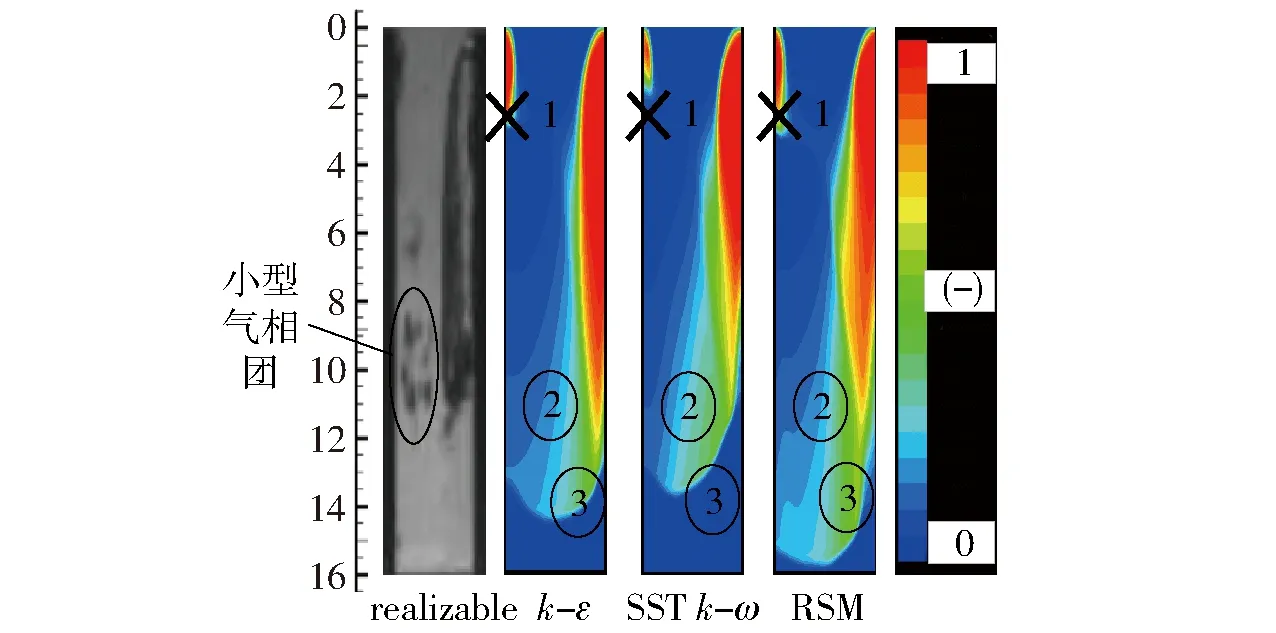
图6 喷孔内气相区域与试验结果对比Fig.6 Comparison between simulation and experiment results of gas phase region in nozzle

分析可知，在点1处，采用SSTk-ω湍流模型计算所得湍流粘度最大，导致流体在该点处流速最小、静压最高，于是在点1及其周围区域计算所得气相体积分数相较采用另外2个湍流模型时更少；在点2处，采用SSTk-ω湍流模型计算所得湍流粘度最小，导致流体在该点处流速最大、静压最低，于是气相在点2及其周围区域发生的扩散现象相较采用另外2个湍流模型时更为严重；在点3处，采用RSM湍流模型计算所得湍流粘度最小，导致流体在该点处流速最大、静压最低，于是气相在点3及其周围区域发生的扩散现象相较采用另外2个湍流模型时更为严重；点1处的气相成分主要为空化效应产生的水蒸气，而点2及点3处的气相成分主要为膨胀后的不凝性气体。综合而言，realizablek-ε湍流模型更为适合喷嘴孔内空化现象数值模拟。

表3 点1、2、3处计算值对比

3 结论

(1)在相同边界条件下，模型1及模型2计算所得气相区域虽然左短右长的分布规律均与试验吻合，然而不考虑不凝性气体及湍流扰动的模型1严重低估了气相区域范围，考虑这2个因素的模型2计算结果则与试验结果吻合良好。分析发现这种差异主要来源于不凝性气体及湍流扰动的影响，一方面不凝性气体会在流场低压区发生膨胀，从而加大最终计算所得气相区域，另一方面湍流扰动对饱和蒸汽压的修正作用，会提高空化效应发生的临界压力，从而促进空化效应，即加强流场内液相至气相的相变过程。在多相流计算采用均相流模型的前提下，不凝性气体及湍流扰动对喷嘴孔内空化现象的准确数值模拟具有重要作用，不可忽略。

(2)考虑不凝性气体及湍流扰动的模型2计算所得气相区域会在其末端位置发生一定程度的扩散现象，这种扩散现象主要来源于不凝性气体在气相区域末端低压区的膨胀作用。

(3)湍流粘度的准确计算对喷嘴孔内空化现象的准确数值模拟具有一定影响，较高的湍流粘度会降低流场内流速，从而提高其静压，最终减弱空化效应及不凝性气体的膨胀作用；反之，较低的湍流粘度会提高流场内流速，从而降低其静压，最终加强空化效应及不凝性气体的膨胀作用。

1 颜学升. 柴油机喷嘴结构对喷雾特性的影响研究[D]. 镇江: 江苏大学, 2013. YAN Xuesheng. Researches on the influences of nozzle structure on spray characteristics for diesel engines[D]. Zhenjiang: Jiangsu University, 2013. (in Chinese)

2 张军. 柴油机喷嘴内空化效应的机理及射流破碎特征的研究[D]. 天津:天津大学, 2010. ZHANG Jun. Investigations of cavitation in nozzle and characteristic of breakup for diesel spray[D]. Tianjin: Tianjin University, 2010. (in Chinese)

3 AKIRA Sou, SHIGEO Hosokawa, AKIO Tomiyama. Effects of cavitation in a nozzle on liquid jet atomization[J]. International Journal of Heat and Mass Transfer, 2007, 50(17-18): 3575-3582.

4 AKIRA Sou, SHIGEO Hosokawa, AKIO Tomiyama. Ligament formation induced by cavitation in a cylindrical nozzle[J]. Journal of Fluid Science and Technology, 2008, 3(5): 633-643.

5 AKIRA Sou. Liquid jet deformation induced by cavitation in nozzles of various shapes[C]. SAE Paper 2009-24-0157, 2009.

6 AKIRA Sou, RADITYA Hendra Pratama, TSUYOSHI Tomisaka. Cavitation flow in nozzle of liquid injector[C]∥ICLASS 2012-12th Triennial International Conference on Liquid Atomization and Spray Systems, 2012.

7 RADITYA Hendra Pratama, AKIRA Sou. String cavitation in fuel injector[C]∥微粒化シンポジウム講演論文集22, 2013:45-51.

8 ARCOUMANIS C, BADAMI M, GAVAISES M. Cavitation in real-size multi-hole diesel injector nozzles[C]. SAE Paper 2000-01-1249, 2000.

9 COLLICOTT S, LI H. True-scale true-pressure internal flow visualization for diesel injectors[C]. SAE Paper 2006-01-0890, 2006.

10 何志霞，柏金，王谦，等. 柴油机喷嘴内空穴流动可视化试验与数值模拟[J]. 农业机械学报，2011, 42(11): 6-9,5. HE Zhixia, BAI Jin, WANG Qian, et al. Visualization experiment and numerical simulation for cavitating flow in a diesel injector nozzle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(11): 6-9，5. (in Chinese)

11 GAVAISES M, ANDRIOTIS A, PAPOULIAS D, et al. Characterization of string cavitation in large-scale diesel nozzles with tapered holes[J]. Physics of Fluids, 2009, 21(5): 107-115.

12 STANLEY C, BARBER T, MILTON B, et al. Periodic cavitation shedding in a cylindrical orifice[J]. Experiments in Fluids, 2011, 51(5):1189-1200.

13 ZHONG Wenjun, HE Zhixia, WANG Qian. Experimental study of flow regime characteristics in diesel multi-hole nozzles with different structures and enlarged scales[J]. International Communications in Heat and Mass Transfer, 2014, 59(10): 1-10.

14 仇滔，宋鑫，雷艳，等. 柴油机喷孔内空化过程与流动特性研究[J/OL]. 农业机械学报，2016, 47(9): 359-365.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160948&flag=1. DOI=10.6041/j.issn.1000-1298.2016.09.048. QIU Tao, SONG Xin, LEI Yan, et al. Cavitation process and flow characteristics inside diesel injector nozzle[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(9):359-365. (in Chinese)

15 BARIS B, TANAKA A, FUKUDA T, et al. Numerical simulation of cavitation phenomenon in diesel injector nozzles[C]∥Proceedings of the 16th Annual Conference ILASS-ASIA, 2013:58-65.

16 HAGAR Alm El-Din Bastawissi, MEDHAT Elkelauy. Computational evaluation of nozzle flow and cavitation characteristics in a diesel injector[C]. SAE Paper 2012-01-1652, 2012.

17 GIANNADAKIS E, PAPOULIAS D, GAVAISES M. Evaluation of the predictive capability of diesel nozzle cavitation models[C]. SAE Paper 2007-01-0245, 2007.

18 AKIRA Sou, BARIS Bicer, AKIO Tomiyama. Numerical simulation of incipient cavitation flow in a nozzle of fuel injector[J]. Computers & Fluids, 2014, 103(8): 42-48.

19 何志霞，陈驭航，纪长浩. 多孔孔板水力空化可视化与数值模拟[J/OL]. 农业机械学报，2016, 47(2): 396-401.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160253&flag=1. DOI=10.6041/j.issn.1000-1298.2016.02.053. HE Zhixia, CHEN Yuhang, JI Changhao. Visualization and numerical simulation of hydrodynamic cavitation in multi-hole orifice plate[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(2):396-401. (in Chinese)

20 HINZE J O. Turbulence[M]. 2nd Ed. New York: McGraw Hill, 1975.

21 CHRISTOPHER Earls Brennen. 空化与空泡动力学[M]. 王勇，潘中永，译.镇江: 江苏大学出版社, 2013.

22 SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]∥Proceedings of the 4th International Conference on Multiphase Flow, 2001.

23 DANIEL Duke, ANDREW Swantek. X-ray imaging of cavitation in diesel injectors[C]. SAE Paper 2014-01-1404, 2014.

Effects of Noncondensable Gases and Turbulent Fluctuations on Cavitation Phenomenon in Injector Nozzle

MA Bin GAO Ying LIU Yu LIU Hongqi CHEN Wei XU Yingjian

(StateKeyLaboratoryofAutomobileSimulationandControl，JilinUniversity，Changchun130025，China)

Fuel spray atomization strongly affected engine economic performance and emissions, which in turn was significantly influenced by nozzle cavitation phenomenon with the high injection pressure in diesel and GDI engine. Aiming to study the influence of noncondensable gases and turbulent pressure fluctuations on modeling of nozzle cavitation, Schnerr and Sauer cavitation model and Singhal cavitation model were used to model nozzle cavitation, which were both coupled with homogeneous equilibrium multiphase model and realizablek-εturbulence model. Then, the Singhal cavitation model was used to model nozzle cavitation with homogeneous equilibrium model and different turbulence models. The comparison of simulation results and experimental results showed that noncondensable gases and turbulent pressure fluctuations had significant impact on modeling nozzle cavitation. The simulation result ignoring noncondensable gases and turbulent pressure fluctuations seriously underestimated the volume fraction of gas phase in nozzle, which was just 42% of the experimental results, while the volume fraction of gas phase calculated by the one considering turbulent pressure fluctuations and noncondensable gases agreed well with experimental results, which was 96% of the experimental results. The results indicated that considering noncondensable gases and turbulent pressure fluctuations would improve accuracy of nozzle cavitation simulation. The calculated gas phase considering noncondensable gases and turbulent pressure fluctuations was diffused to some extent at the end of gas phase region, which was caused by the expansion of noncondensable gases in fluid. Turbulence viscosity slightly affected the distribution of gas phase by affecting the velocity and pressure of fluid.

injector; cavitation; numerical simulation; noncondensable gases; turbulent disturbance

10.6041/j.issn.1000-1298.2017.04.045

2016-08-11

2016-09-09

国家自然科学基金项目(51306069)

麻斌(1989—)，男，博士生，主要从事直喷汽油机喷嘴内空化效应机理及射流破碎特征研究, E-mail： mb_freedom@sina.cn

高莹(1972—)，女，教授，博士生导师，主要从事整车热管理、内燃机流动和燃烧研究，E-mail： ying-gao@vip.sina.com

TK417

A

1000-1298(2017)04-0342-07