不同土壤前期含水率和坡度下黄壤分离临界水动力特性
王晨沣 王 彬,2 王玉杰,2 王云琦,2 胡 波 李世荣
(1.北京林业大学水土保持学院, 北京 100083;2.北京林业大学重庆缙云山三峡库区森林生态系统国家定位观测研究站, 北京 100083;3.北京市水土保持工作总站, 北京 100036)
不同土壤前期含水率和坡度下黄壤分离临界水动力特性
王晨沣1王 彬1,2王玉杰1,2王云琦1,2胡 波1李世荣3
(1.北京林业大学水土保持学院, 北京 100083;2.北京林业大学重庆缙云山三峡库区森林生态系统国家定位观测研究站, 北京 100083;3.北京市水土保持工作总站, 北京 100036)
土壤分离临界水动力学参数是侵蚀预报研究的基础内容,但关于不同近地表土壤水分条件下坡面侵蚀发生临界起动关键影响因子及其内在机制尚不清楚。本研究选取长江中上游地区典型黄壤为研究对象,试验设计5个土壤前期含水率(5%~23%)和5个坡度(1.0°~10.0°),利用冲刷槽实测土壤分离临界水动力学参数,探讨土壤分离临界水动力学参数对不同土壤前期含水率和坡度耦合作用的响应。结果表明:土壤分离临界流速、临界水深和流态均与坡度和土壤前期含水率呈幂函数减小关系;在坡度小于5.0°时,土壤分离临界水动力参数受坡度和土壤前期含水率耦合作用的影响;而在坡度大于5.0°时则主要受坡度的影响。因此,当坡度大于5.0°时,可直接采用简化幂函数方程对土壤分离临界水动力参数进行估算。在本研究试验条件下,坡面土壤分离临界水流流态基本属于层流、缓流,发生紊流、急流的概率很小。坡度和土壤前期含水率对坡面流阻力有重要的影响,阻力系数随临界单宽流量和雷诺数的增加呈幂函数下降趋势。
土壤分离; 土壤前期含水率; 坡度; 临界水动力特性; 黄壤
引言
土壤侵蚀已成为重要的环境问题之一,水土流失将带来一系列的环境、社会和经济问题[1-2]。土壤侵蚀的三大主要过程为:土壤分离、输移和沉积,而土壤分离是精准预报土壤侵蚀物理模型的核心需求之一[3-4]。目前研究多集中于径流冲刷对土壤分离的作用与贡献[5-7],并认为径流分离土壤颗粒是侵蚀泥沙的主要来源[8]。国内外许多学者也试图利用土壤分离速率与水动力学参数(如水流剪切力、水流功率、雷诺数、弗汝德数等)建立函数关系以获取土壤临界坡度[9]、临界径流剪切力[10]和临界水流功率[11],并取得了一定成果[12-14]。但是,这些研究大都是在设定的近地表土壤水分条件下进行,忽视了不同近地表土壤水文条件对坡面土壤分离临界水动力参数的影响,研究结果只符合某个特定条件的规律且具有明显的局限性。
近地表土壤水文条件包括自由下渗、土壤水分饱和、壤中流等[15],主要与土壤前期含水率有关,土壤前期含水率是影响坡面土壤侵蚀过程的一个重要因素。近期,SIMON等[16]和FOX等[17]通过试验表明近地表水文条件对土壤分离速率的变化具有决定性作用,此后受到越来越多研究者的重视[18-20]。在径流冲刷条件下,不同前期近地表水文条件对土壤分离速率和临界水动力特性的影响尚未引起足够的关注。特别是通过实测方法探讨不同土壤前期含水率和坡度对土壤分离临界水动力特性的定量影响鲜见报道。NOUWAKPO等[21]实测出土壤颗粒起动临界径流剪切力随着水力梯度的增加而减小。雷廷武等[22]在土壤饱和的情况下实测出细沟再生临界流量、剪应力与坡度的关系。但以上研究仅为不同近地表水文条件或不同坡度对土壤分离临界水动力特性的影响,缺乏系统的对比性。因此,开展土壤前期含水率和坡度耦合作用对坡面土壤分离临界水动力学特性的影响研究,对于分析和建立坡面侵蚀预报模型具有重要意义。
长江中上游地区是中国土壤侵蚀最为严重的地区之一,坡面侵蚀是该地区土壤侵蚀泥沙量的主要来源[23]。冲刷条件下坡面土壤分离临界水动力学参数的判定多数由经验值计算得到,由于侵蚀过程的测量存在很大变异性,通过经验值计算得到的临界值是否具有可靠性尚不能确定。在人工模拟降雨条件下,有关土壤前期含水率对侵蚀产沙的研究取得了许多重要的成果[24-26],但在径流冲刷条件下的相关研究较少。因此,本文以长江中上游地区重要土壤资源之一的黄壤为研究对象,通过实测不同土壤前期含水率(5%~23%)和坡度(1.0°~10.0°)条件下黄壤坡面土壤分离临界水动力学参数,对比分析土壤颗粒临界起动条件随前期含水率及坡度的变化趋势,以期为黄壤侵蚀防治提供理论支持和科学指导。
1 材料与方法
1.1 研究区概况
研究区位于长江中上游三峡库区重庆市北碚区,地处嘉陵江温塘峡西岸的缙云山自然保护区内(106°22′E、29°45′N)。该区域亚热带季风湿润性气候明显,年均降水量1 611.8 mm,年均蒸发量777.1 mm,年均气温13.6℃。降水多集中在4—9月份,降水量占全年的77.2%。其中在7月下旬—8月中旬属伏旱期,降水量少,由于连日的高温干旱天气导致蒸发量大,约占全年蒸发量的32.9%。地貌以丘陵、山地为主,海拔高度最高为951.5 m,其相对高差为600 m。该区降水量较大,主要以水力侵蚀为主。黄壤是重庆市重要的土壤资源,是重庆山区主要旱粮和多经用地,同时也是林业基地,其面积约为237.2万hm2,占土地总面积的28.78%。研究区主要植被类型有常绿阔叶林、暖性针叶林、竹林、灌草丛植被等,其中大面积乔木、灌草植被受到破坏退化或人为因素的影响而形成裸露地带。主要优势树种有香樟(Cinnamomumcamphora)、马尾松(Pinusmassoniana)、杉木(Cunninghamialanceolata)、四川大头茶(Gordoniaacuminata)和四川山矾(Symplocossetchuanensis)等。本研究供试土壤选取弃耕多年后裸露地带的黄壤,土壤颗粒质地划分采用美国农业部制,黄壤质地属于粉质粘壤土,其中砂粒(50~2 000 μm)、粉粒(2~50 μm)、粘粒(0~2 μm)的质量分数分别为13.7%、54.2%和32.1%,土壤液限(碟式液限仪法)为33.9%,塑限(搓条法)为23.8%,土壤有机质(重铬酸钾氧化-外加热法)质量比为31.8 g/kg。
1.2 试验装置与材料
试验于2015年6—8月份在北京林业大学缙云山国家定位观测研究站人工模拟降雨试验场进行。试验在长4 m、宽0.4 m、高0.1 m的冲刷槽内进行,可控坡度为0°~30°。在冲刷槽的顶端有1个深度0.40 m的稳流池,确保入流的水流有稳定的水头,尾端通过固定装置连接土壤放样室。供水系统由蓄水池、水泵、阀门和管道组成,并在管道处串联压力表和流量计,通过阀门进行流量调节(图1)。

图1 试验装置示意图Fig.1 Sketch of experiment device1.稳流池 2.流量计 3.压力表 4.流量调节阀 5.水泵 6.蓄水池 7.沉沙池 8.土壤床
1.3 研究方法
1.3.1 试验设计
鉴于研究区夏季炎热多雨的天气特点并结合实测裸地含水率数据,设计5个土壤前期含水率:5%(风干含水率)、8%、13%、18%和23%;缙云山裸地坡度范围5°~10°,故设计5个缓坡坡度:1.0°、2.5°、5.0°、7.5°和10.0°。依据土壤分离速率随坡度和流量的变化呈正相关关系[3]以及土壤可蚀性随土壤前期含水率的增加而增大的规律[27],通过预试验确定土壤前期含水率为5%、坡度为1.0°和土壤前期含水率为23%、坡度为10.0°的土壤分离临界流量,从而确定设计流量范围为0.01~0.20 L/s。各处理3次重复,对所有试验数据取平均值计算标准偏差(SD)。
1.3.2 试验方法
土样采自深度0~5 cm土壤,风干后过2 mm土壤筛以备测试使用。将尺寸为0.2 m×0.4 m×0.1 m(长×宽×深)的土壤环刀通过固定装置与冲刷槽尾端相连;随后将填装不同黄壤前期含水率的土壤环刀缓慢放入冲刷槽中备用。为保证填装土样的均匀性,试样采用分层装土,每2.5 cm填装土样一次,共装4层。填土时边填充边压实,每一层填装完毕后进行抛毛;通过雾状喷雾器调节每层填装土壤含水率以达到设计要求,填装完毕后将土样密封静置24 h使土壤水分达到均匀扩散后进行试验。缙云山裸地表层土壤容重范围1.12~1.20 g/cm3,故试验容重控制在1.20 g/cm3左右。
径流冲刷条件下的土壤分离过程是指土壤颗粒脱离母质的过程[28],当作用于土壤表面的水流动力或能量大于等于其临界值时,土壤颗粒则发生分离[29-30]。因此,参照NOUWAKPO等[21]通过改变流量直到土壤颗粒被分离时测定土壤分离临界值的方法,该研究在调整好冲刷槽坡度后,起动水泵通过流量调节阀门从小到大逐渐增加流量,直到土壤床面颗粒出现连续不断被分离为止,记录土壤分离临界时刻的流量和水位,即土壤分离临界流量和水深的实测值。临界流量通过计算单位时间内过水断面的径流量得到(采用量程为60 kg的电子秤进行称量,精度为0.001 kg)。临界水位通过探针法测定,分别在距冲刷槽尾端0.5 m、1.0 m和1.5 m的3个横断面测定水深,每个断面在中心区域等间隔测4个点,去除极大值和极小值后将剩余10个水深进行平均得到平均水深,水位探针的精度为0.01 cm。临界水动力参数通过实测的临界流量和水深计算得到,即临界水动力参数的实测值,其计算公式如下:
平均流速的计算公式为
(1)
式中v——平均流速,m/sQ——流量,m3/sB——断面宽度,mh——水深,m
雷诺数的计算公式为
(2)
其中γ=0.017 75/(1+0.033 7t+0.000 221t2)
式中Re——雷诺数R——水力半径,mγ——动力粘滞系数,cm2/st——水温,℃
弗汝德数的计算公式为
(3)
式中Fr——弗汝德数g——重力加速度,取9.8 m/s2
达西阻力系数的计算公式为
(4)
其中J=sinθ
式中f——达西阻力系数J——水流能坡θ——坡度
1.3.3 坡度和土壤前期含水率的标准化处理
采用均值转化的处理方法统一坡度和土壤前期含水率的量纲,即
(5)
其中
式中λ——坡度i和土壤前期含水率j因素m——某一因素的数据序列N——数据序列的长度xλ(m)——坡度i和土壤前期含水率j因素的数据序列
2 结果与分析
坡面平均流速、平均水深、雷诺数、弗汝德数及阻力系数是反映水力学特性的重要指标,依据明渠水力学原理和方法,利用经验公式计算不同水平下坡面侵蚀发生时的水力学参数,结果如表1所示。
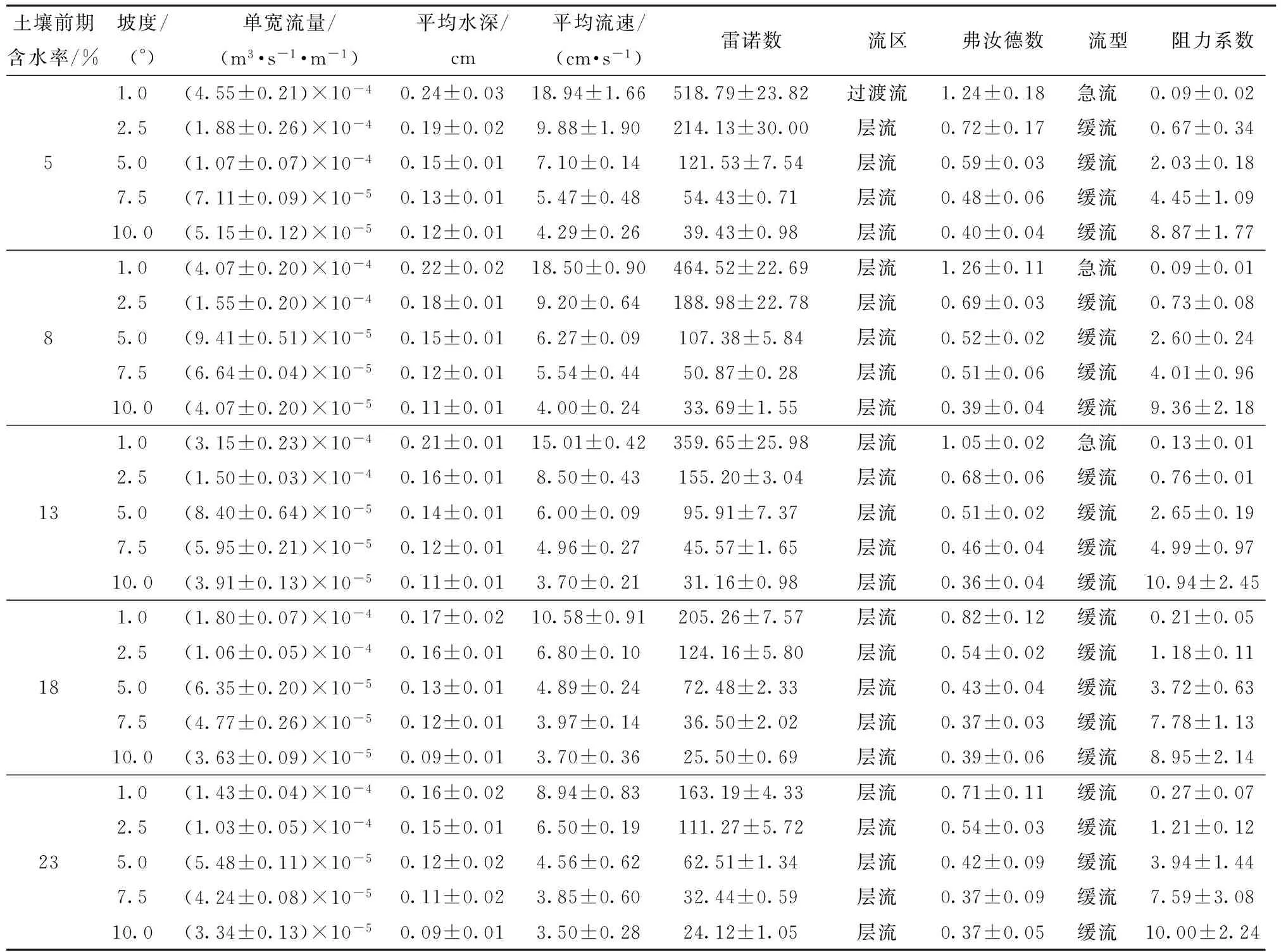
表1 不同坡度和土壤前期含水率下土壤分离临界水动力学特性试验结果
2.1 土壤前期含水率和坡度耦合作用对坡面土壤分离临界流速的影响
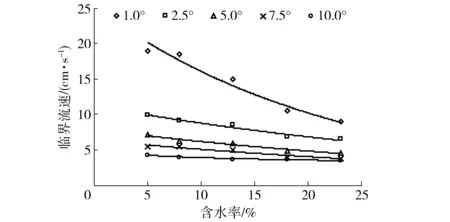
图2 土壤分离临界流速与土壤前期含水率的关系Fig.2 Relationship between critical flow velocity for soil detachment and antecedent soil moisture content
平均流速是土壤侵蚀预报中重要的水动力学参数,可从整体上反映坡面薄层水流的状况[3]。随着土壤前期含水率的增加,土壤分离临界流速基本呈指数减小(R2>0.92)(图2);而临界流速与坡度呈幂函数减小关系(R2>0.97)(图3)。随着土壤前期含水率的增加,坡度越小,临界流速下降的趋势越大(图2)。坡度为1.0°的临界流速减小了10 cm/s;而随着坡度的增加,下降不明显,特别是坡度10.0°的临界流速仅减小了0.79 cm/s。虽然黄壤坡面土壤分离临界流速随着坡度的增加而减小,但其变化趋势与土壤前期含水率有所不同。含水率越小,临界流速随坡度的增加变化趋势越大(图3)。当含水率为5%时临界流速减小了14.65 cm/s;而含水率为23%时临界起动流速减小了5.44 cm/s。随着土壤前期含水率的增加,临界流速在较小坡度下降的更快,而坡度越大临界流速下降的趋势越缓慢;不同土壤前期含水率下,临界流速在坡度为1.0°~5.0°时快速下降,而在坡度为5.0°~10.0°时下降较缓慢。通过偏相关分析发现,坡度和土壤前期含水率与临界起动流速的偏相关系数r分别为-0.83、-0.53,p值小于0.01。说明土壤分离临界流速是坡度和土壤前期含水率耦合作用的结果。通过回归方程得出临界流速与坡度和土壤前期含水率呈幂函数关系
Vc=0.599 8S-0.584 1M-0.370 0(R2=0.95,n=25)
(6)
式中Vc——土壤分离临界流速,cm/sS——坡度的正切值M——土壤前期含水率,%
利用均值标准化处理方法,消除坡度和土壤前期含水率因素的量纲影响后的回归拟合结果为
ZVc=5.106 8S-0.584 1M-0.370 0(R2=0.95,n=25)
(7)
式中ZVc——Vc的标准化值,cm/s
式(7)表明临界流速和坡度、土壤前期含水率存在极显著幂函数相关关系;且坡度的绝对幂指数是土壤前期含水率的1.59倍,说明土壤前期含水率对临界流速的影响小于坡度。故将式(6)简化为坡度与临界流速间的简单幂函数关系
Vc=1.432 3S-0.568 3(R2=0.77,n=25)
(8)

图3 坡面侵蚀发生临界流速与坡度的关系Fig.3 Relationship between critical flow velocity for soil detachment and slope gradient
以土壤前期含水率8%和18%为例,土壤分离临界流速实测值与式(8)拟合值的关系如图4所示,当坡度小于5.0°时,土壤前期含水率8%和18%临界流速偏离1∶1线,而坡度大于5.0°时和1∶1线较接近。这证明了在坡度大于5.0°时,利用式(8)对土壤分离临界流速进行估算更为合适。RAUWS等[31]认为在土壤前期含水率为饱和情况下的粉壤土中,2~6 cm/s的流速范围是细沟侵蚀发生的临界水力学临界值。而有的学者在加拿大室内和室外以及在黄土高原地区利用模拟降雨表明坡面上细沟发生的临界流速为7~8 cm/s[32]。该值小于本研究得出的土壤分离临界流速范围3.50~18.94 cm/s。随着土壤前期含水率的增加,临界流速呈减小趋势,最终达到一个稳定的状态,并且不同坡度间的变化范围也在减小(图2)。利用式(6)预测土壤饱和情况下土壤分离临界流速范围为2.20~8.51 cm/s,说明临界流速受坡度和土壤前含水率耦合作用的影响。相关研究也表明随着土壤前期含水率和坡度的增加,土壤更易于被侵蚀,土壤可蚀性增加[27,33],并随着坡面侵蚀发生临界流量的减小,土壤侵蚀发生临界流速呈减小的趋势[34]。

图4 不同前期含水率土壤分离临界流速实测值与预测值的关系Fig.4 Relationship between measured and predicted critical flow velocities of soil detachment under different antecedent soil moisture contents
2.2 土壤前期含水率和坡度耦合作用对坡面土壤分离临界水深的影响
随着土壤前期含水率的增加,土壤分离临界水深呈线性减小的趋势(R2>0.88)(图5);而土壤分离临界水深与坡度呈幂函数减小关系(R2>0.90)(图6)。土壤分离临界水深范围在0.09~0.24 cm之间。随着土壤前期含水率的增加,临界水深下降趋势越小。当坡度为1.0°时,土壤前期含水率从5%增加到23%时临界水深降低了33.33%;临界水深最小降低了15.38%。随着坡度的增加,土壤前期含水率为5%~23%时的临界水深降低幅度为43.75%~50.00%。出现上述现象是因为随土壤前期含水率和坡度的增加,土壤更易于侵蚀,而水深代表着坡面流水动力。因此,随着土壤前期含水率和坡度的增加,临界水深呈减小的趋势。与临界流速类似,坡度和土壤前期含水率越小,土壤分离临界水深变化幅度越大;反之,变化幅度越小。这也充分说明不同土壤前期含水率和坡度的变化同样与临界径流剪切力和水流功率呈某种函数关系。深入分析发现,临界水深与坡度、土壤前期含水率呈幂函数关系
Dc=4.70×10-2S-0.265 4M-0.183 0(R2=0.94,n=25)
(9)
式中Dc——土壤分离临界水深,cm
利用均值标准化处理方法,消除坡度和土壤前期含水率因素的量纲影响后的回归拟合结果为
ZDc=0.128 1S-0.265 4M-0.183 0(R2=0.94,n=25)
(10)
式中ZDc——Dc的标准化值,cm
与临界流速类似,在坡度小于5.0°时采用式(9),当坡度大于5.0°时采用简单的幂函数
Dc=7.07×10-2S-0.2622(R2=0.77,n=25)
(11)
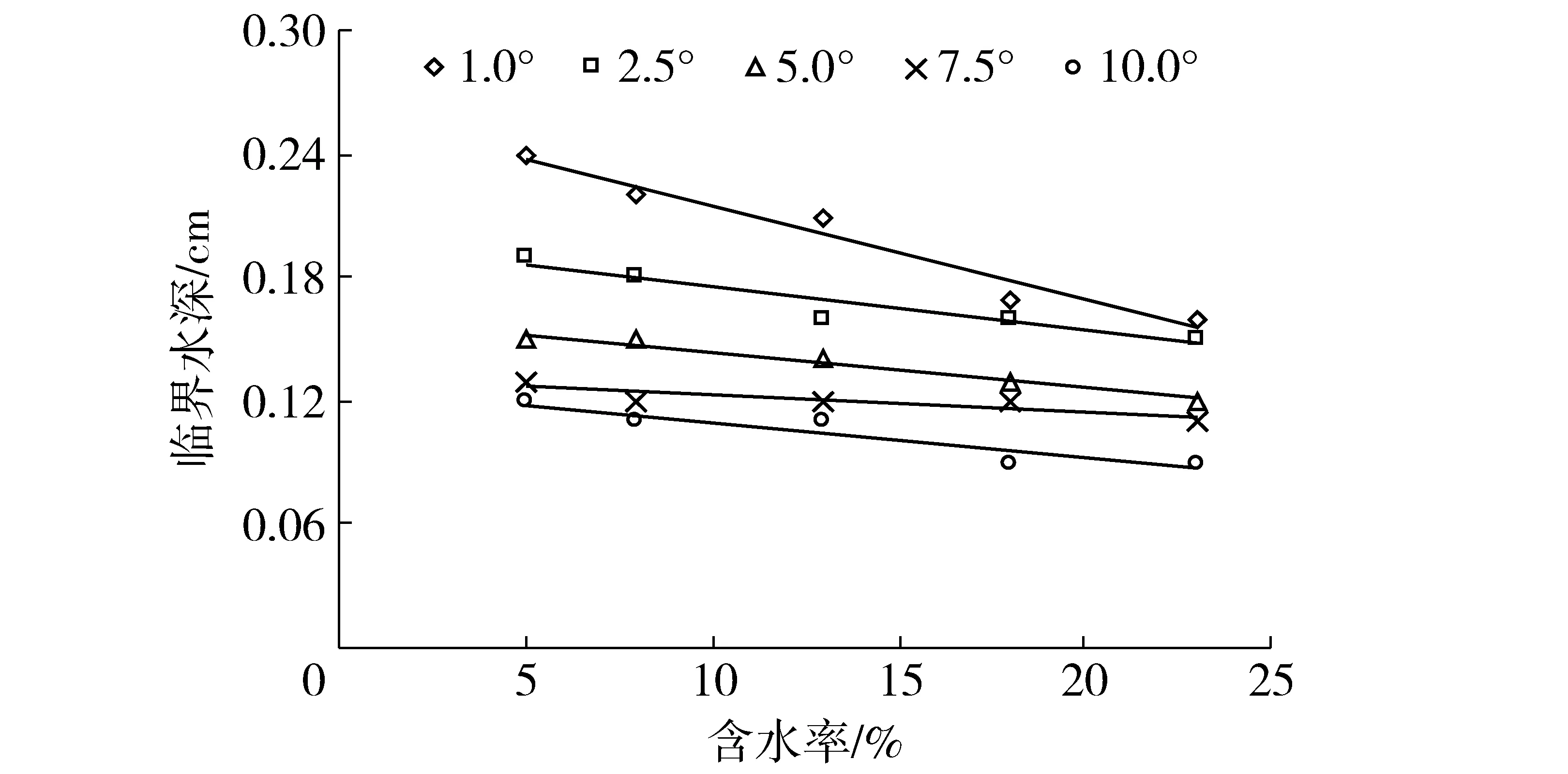
图5 土壤分离临界水深与土壤前期含水率的关系Fig.5 Relationship between critical flow depth for soil detachment and antecedent soil moisture content

图6 土壤分离临界水深与坡度的关系Fig.6 Relationship between critical flow depth for soil detachment and slope gradient
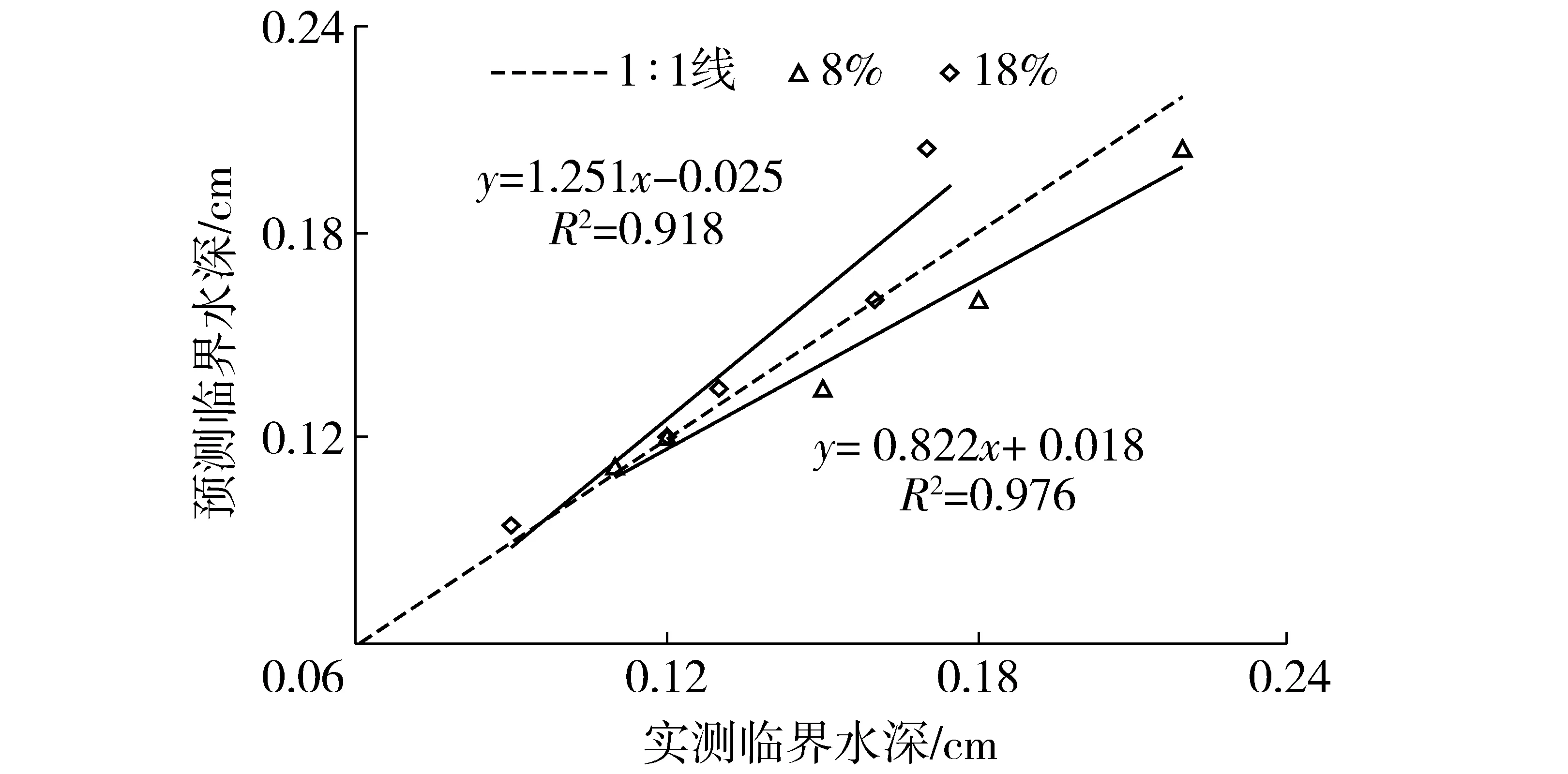
图7 不同前期含水率土壤分离临界水深实测值与预测值的关系Fig.7 Relationship between measured and predicted critical flow depths of soil detachment under different antecedent soil moisture contents
以土壤前期含水率8%和18%为例,当坡度小于5.0°时,土壤前期含水率8%和18%临界水深偏离1∶1线越来越远,而坡度大于5.0°时和1∶1线较接近(图7)。这证明了在坡度大于5.0°时,利用式(11)对土壤分离临界流速进行估算更为合适。
2.3 土壤前期含水率和坡度耦合作用对坡面土壤分离临界流态的影响
水流流态是研究坡面薄层水流水动力学的基本参数,并与坡面侵蚀发生有着密切关系,坡面流流态包括流区和流型两类[35]。流区包括层流、紊流和过渡流;流型包括缓流、急流和介于二者间的临界流。一般来说,缓流、层流的紊动微弱,侵蚀能力小;急流、紊流则相反。
不同土壤前期含水率下,随坡度的增加,土壤分离临界时刻的雷诺数和弗汝德数呈减小趋势(图8)。在坡度1.0°~5.0°时,雷诺数随着土壤前期含水率的增加具有明显的降低趋势;相对而言,在坡度5.0°~10.0°时,降低趋势则不明显。土壤分离临界水流流区基本属于层流,雷诺数为24.12~518.79,而张科利等[36]发现在坡度3°~10°和土壤前期含水率为饱和条件下细沟侵蚀发生临界雷诺数在50~350之间。本研究涉及的坡度低至1.0°,加之土壤前期含水率为5%~23%远低于饱和状态,刘振波等[33]表明随着土壤前期含水率的增加,土壤可蚀性增加,所以本文所得出流区范围要更大。除坡度为1.0°土壤前期含水率为5%的雷诺数属于过渡流外,其他处理均属于层流状态(表1)。弗汝德数变化趋势与雷诺数变化规律相似,随着坡度和土壤前期含水率的增加均呈减小趋势。弗汝德数仅坡度为1.0°土壤前期含水率小于18%时大于1,为急流;其他均小于1,为缓流。本文所得出的弗汝德数为0.37~1.26。深入分析表明,雷诺数、弗汝德数与坡度和土壤前期含水率呈幂函数关系
Re=2.123 7S-0.934 3M-0.589 5(R2=0.96,n=25)
(12)
Fr=0.095 6S-0.440 6M-0.261 0(R2=0.94,n=25)
(13)
利用均值标准化处理方法,消除坡度和土壤前期含水率因素的量纲影响后的回归拟合结果为
ZRe=64.977 3S-0.934 3M-0.589 5(R2=0.96,n=25)
(14)
ZFr=0.463 4S-0.440 6M-0.261 0(R2=0.94,n=25)
(15)
式中ZRe——Re的标准化值ZFr——Fr的标准化值
式(14)、(15)表明雷诺数、弗汝德数均与坡度、土壤前期含水率存在极显著幂函数相关关系;且坡度的绝对幂指数是土壤前期含水率的1.58倍以上,说明土壤前期含水率对雷诺数、弗汝德数的影响要小于坡度。故将式(12)、(13)简化为坡度与雷诺数、弗汝德数的简单幂函数关系
Re=8.981 8S-0.901 2(R2=0.73,n=25)
(16)
Fr=0.174 2S-0.431 6(R2=0.79,n=25)
(17)
与式(12)、(13)相比,式(16)、(17)决定系数分别降低了23.96%、15.96%。不同土壤含水率在坡度小于5.0°时,雷诺数和弗汝德数变化较大,而在坡度大于5.0°时变化很小,在坡度为10.0°时基本趋于一致(图8)。因此,当坡度大于5.0°时可直接采用简化幂函数方程对土壤分离临界水动力参数进行估算(式(16)、(17))。以土壤前期含水率8%和18%为例,当坡度小于5.0°时,土壤前期含水率8%、18%的雷诺数和弗汝德数偏离1∶1线越远,而坡度大于5.0°时和1∶1线较接近(图9)。这证明了在坡度大于5.0°时,利用式(16)、(17)对土壤分离临界流速进行估算更为合适。
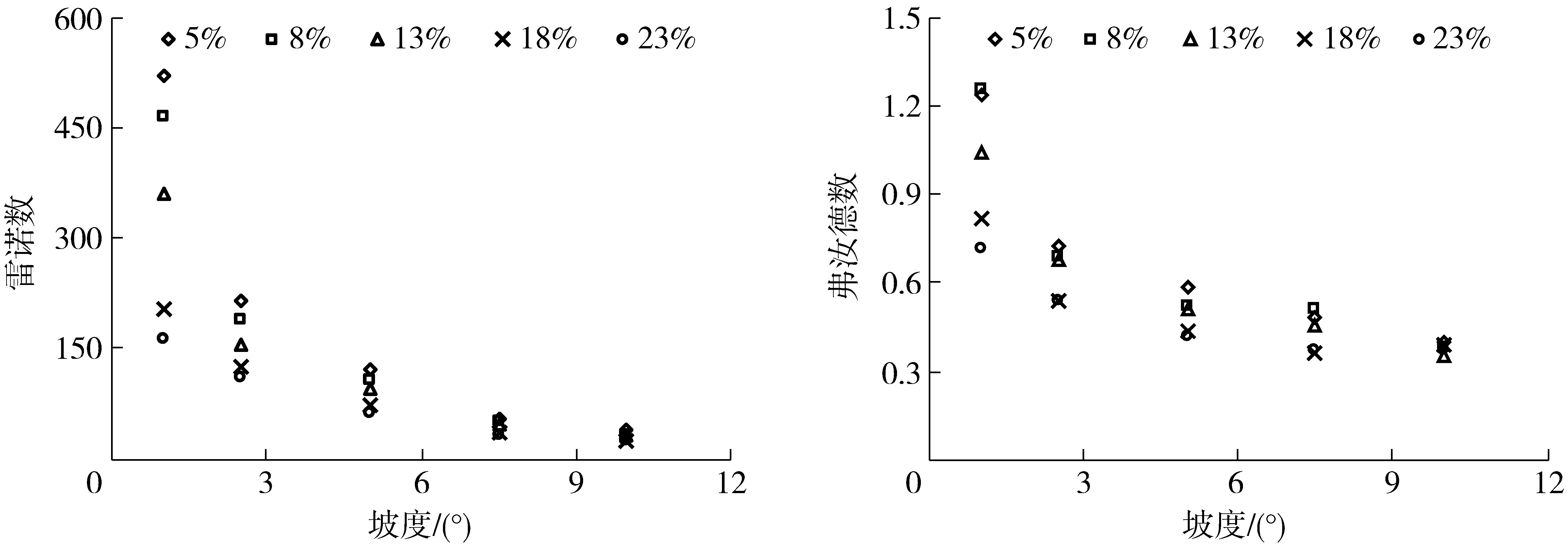
图8 不同土壤前期含水率下土壤分离流态与坡度的关系Fig.8 Relationships of pattern for soil detachment and slope gradient under different antecedent soil moisture contents
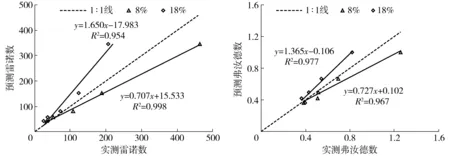
图9 不同前期含水率土壤分离流态实测值与预测值的关系Fig.9 Relationships of measured and predicted patterns of soil detachment under different antecedent soil moisture contents
2.4 土壤前期含水率和坡度耦合作用对坡面土壤分离阻力系数的影响
Darcy-Weishbach阻力系数反映了下垫面对流动水体的阻力,它是坡面流水动力学基本参数之一。在流量和坡度等水力条件相同的情况下,阻力系数越大,说明径流克服阻力所消耗能量越多,土壤侵蚀越剧烈。随着坡度和土壤前期含水率的增加,土壤分离临界时刻的阻力系数基本呈增加趋势(表1)。这是因为随着坡度和土壤前期含水率的增加,土壤分离临界单宽流量减小,且临界单宽流量与阻力系数呈幂函数减小趋势(图10)。ABRAHAMS等[37-38]在坡度为0.74°~3.2°的缓坡上得出阻力系数在0.20~2.84之间。GILLEY等[39]认为阻力系数随着坡度和流量的变化很大;随着雷诺数的增加,阻力系数变化于0.17~8之间。有关坡面薄层流阻力系数的研究成果分歧还很大,FORSTER等[40]在坡度1.7°~5.6°范围内得出阻力系数不会超过0.5。本研究得到阻力系数范围为0.09~10.94。阻力系数与雷诺数的关系为f=3 119.4Re-1.660(图11),这与以上研究所得结论相符。是因为随着坡度和土壤前期含水率的增加,雷诺数随之减小,这意味着土壤分离临界水深和流速减小,水深的减小会使相对糙率变大;流速的减小意味着水流强度减小,其结果引起冲刷强度减小,所以使阻力系数增大。
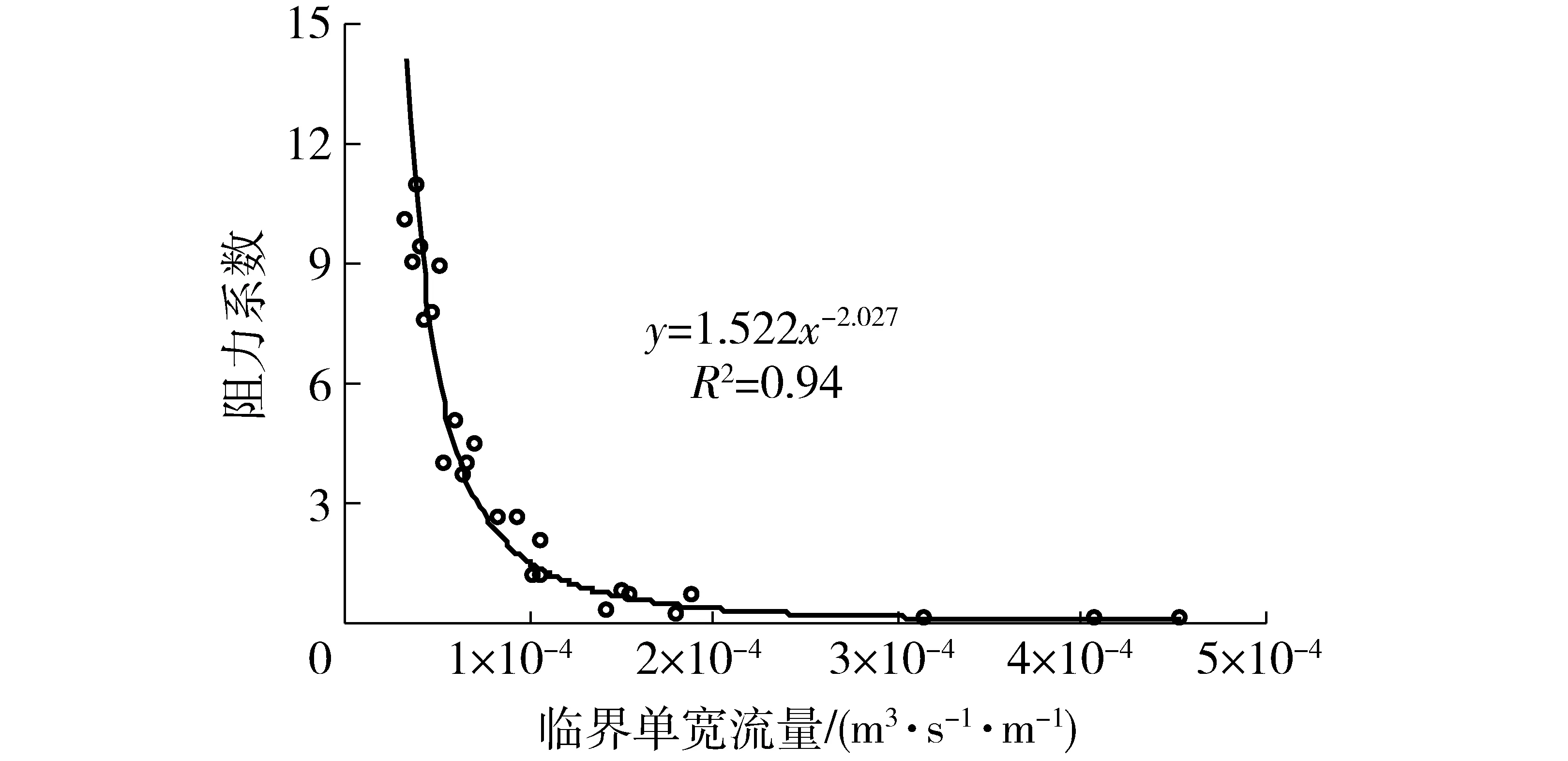
图10 阻力系数与临界单宽流量的关系Fig.10 Relationship between Darcy-Weisbach factor and discharge per unit width
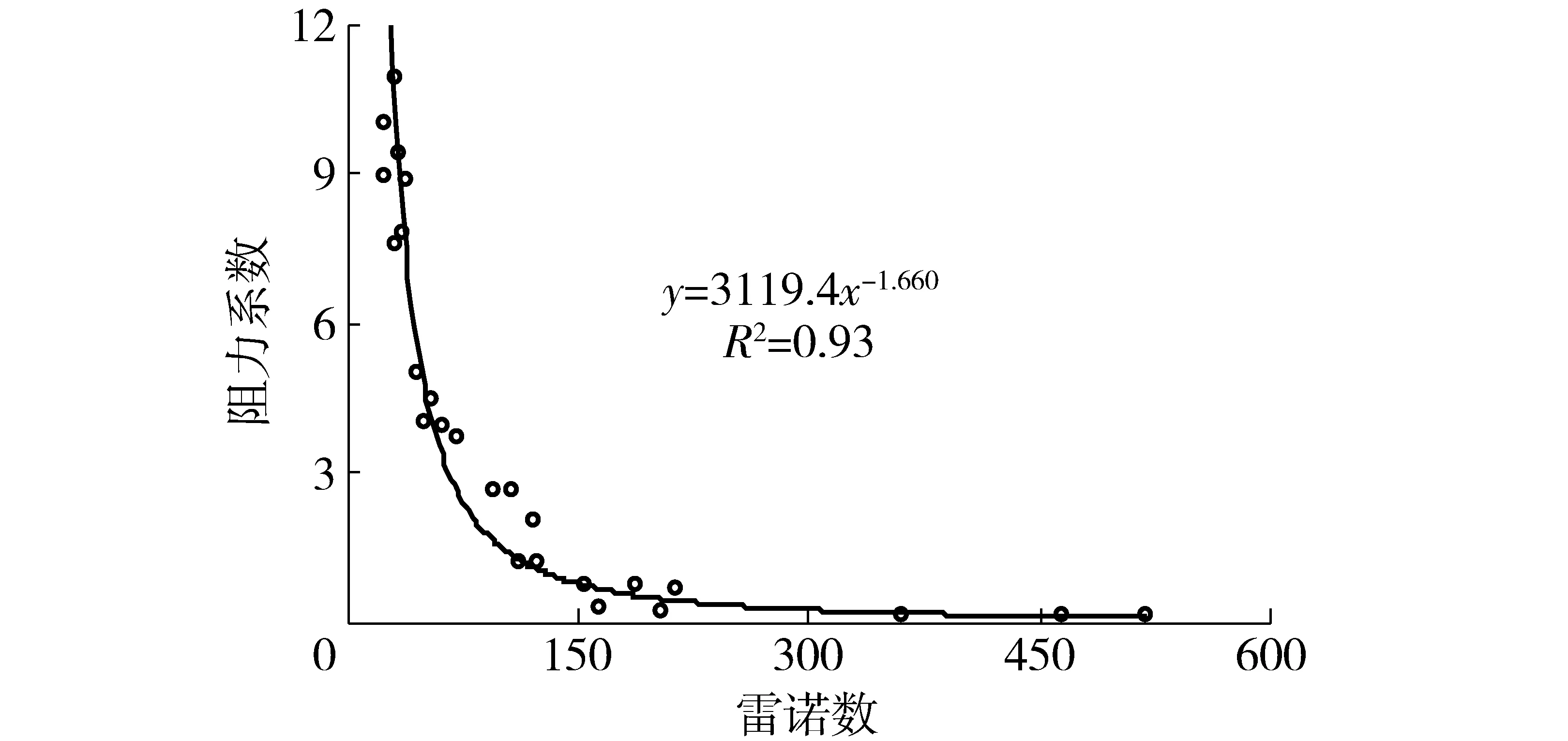
图11 阻力系数与雷诺数的关系Fig.11 Relationship between Darcy-Weisbach factor and Reynolds number
3 结论
(1)土壤分离临界流速、临界水深和流态均与坡度和土壤前期含水率呈幂呈函数减小关系。坡度小于5.0°时,土壤分离临界水动力参数受坡度和土壤前期含水率耦合作用的影响;而在坡度大于5.0°时则主要受坡度的影响。因此,当坡度大于5.0°时,可直接采用简化幂函数方程对土壤分离临界水动力参数进行估算。
(2)土壤分离临界水流流区属于层流,雷诺数变化于24.12~518.79之间。弗汝德数仅在坡度为1.0°土壤前期含水率为5%、8%和13%时大于1,流型为急流;其他均小于1,流型为缓流,弗汝德数范围为0.37~1.26。说明本研究中坡面土壤分离临界水流流态基本属于层流、缓流,发生紊流、急流的概率很小。
(3)坡度和土壤前期含水率对坡面流阻力有重要的影响,阻力系数随临界单宽流量和雷诺数的增加呈幂函数下降趋势。随坡度和土壤前期含水率的增加,土壤分离临界单宽流量减小,同时也意味着临界水深和临界流速减小,导致下垫面对水流的影响较大,从而使得阻力系数变大。
1 WANG Bin, ZHENG Fenli, RÖMKENS M J M. Comparison of soil erodibility factors in USLE, RUSLE2, EPIC and Dg models based on a Chinese soil erodibility database[J]. Acta Agriculture Scandinavica, Section B-Soil & Plant Science, 2013, 63(1): 69-79.
2 郑粉莉,徐锡蒙,覃超.沟蚀过程研究进展[J/OL].农业机械学报,2016,47(8):48-59. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160808&flag=1.DOI:10.6041/j.issn.1000-1298.2016.08.008. ZHENG Fenli, XU Ximeng, QIN Chao. A review of gully erosion process research[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(8):48-59. (in Chinese)
3 何小武,张光辉,刘宝元. 坡面薄层水流的土壤分离实验研究[J].农业工程学报,2003, 19(6):52-55. HE Xiaowu, ZHANG Guanghui, LIU Baoyuan. Soil detachment by shallow flow on slopes [J]. Transactions of the CSAE,2003,19(6):52-55.(in Chinese)
4 FOSTER G R, MEYER L D, ONSTAD C A. An erosion equation derived from basic erosion principles[J]. Transactions of the ASAE, 1977, 20(4): 678-682.
5 赵春红,高建恩,王飞,等.含沙量对坡面流水动力学特性的影响研究[J/OL].农业机械学报,2013, 44(9):79-85. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130915&flag=1.DOI:10.6041/j.issn.1000-1298.2013.09.015. ZHAO Chunhong, GAO Jian’en, WANG Fei, et al. Effects of sediment load on hydrodynamic characteristics of overland flow[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(9):79-85. (in Chinese)
6 马小玲,张宽地,董旭,等.黄土坡面细沟流土壤侵蚀机理研究[J/OL].农业机械学报, 2016,47(9):134-140.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160920&flag=1.DOI:10.6041/j.issn.1000-1298.2016.09.020. MA Xiaoling, ZHANG Kuandi, DONG Xu, et al. Study of rill flow soil erosion mechanism on loess slope surface[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(9):134-140. (in Chinese)
7 杨帆,程金花,张洪江,等.坡面草本植物对土壤分离及侵蚀动力的影响研究[J/OL].农业机械学报, 2016,47(5):129-137. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160518&flag=1.DOI:10.6041/j.issn.1000-1298.2016.05.018. YANG Fan, CHENG Jinhua, ZHANG Hongjiang, et al. Effect of herb plants on soil detachment and erosion dynamics[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(5):129-137. (in Chinese)
8 张光辉. 坡面水蚀过程水动力学研究进展[J].水科学进展,2001,12(3):395-402. ZHANG Guanghui. Advances in study of runoff detachment processes based on hydraulics[J]. Advances in Water Science,2001,12(3):395-402. (in Chinese)
9 李鹏,李占斌,郑良勇. 黄土陡坡径流侵蚀产沙特性室内实验研究[J]. 农业工程学报,2005,21(7):42-45. LI Peng, LI Zhanbin, ZHENG Liangyong. Indoor experiment of characteristics of runoff erosion in loess steep slope [J]. Transactions of the CSAE, 2005, 21(7): 42-45. (in Chinese)
10 李鹏,李占斌,郑良勇,等. 坡面径流侵蚀产沙动力机制比较研究[J]. 水土保持学报,2005,19(3):66-69. LI Peng, LI Zhanbin, ZHENG Liangyong, et al. Comparisons of dynamic meachanics of soil erosion and sediment yield by runoff on loess slope[J]. Journal of Soil and Water Conservation, 2005,19(3):66-69. (in Chinese)
11 丁文峰. 紫色土和红壤坡面径流分离速度与水动力学参数关系研究[J]. 泥沙研究,2010(6):16-22. DING Wenfeng. Relationships between soil detachment rate and runoff hydrodynamic indexes of purple soil slope and red soil slope[J]. Journal of Sediment Research,2010(6):16-22. (in Chinese)
12 NEARING M A, SIMANTON R,NORTON D,et al. Soil erosion by surface water flow on a stony, semiarid hillslope[J]. Earth Surface Processes and Landforms,1999,24(8):677-686.
13 柳玉梅,张光辉,李丽娟,等. 坡面流水动力学参数对土壤分离能力的定量影响[J]. 农业工程学报,2009,25(6):96-99. LIU Yumei, ZHANG Guanghui, LI Lijuan, et al. Quantitative effects of hydro-dynamic parameters on soil detachment capacity of overland flow[J]. Transactions of the CSAE,2009,25(6):96-99. (in Chinese)
14 李鹏,李占斌,郑良勇.黄土坡面径流侵蚀产沙动力过程模拟与研究[J].水科学进展, 2006, 17(4):444-449. LI Peng, LI Zhanbin, ZHENG Liangyong. Hydrodynamics process of soil erosion and sediment yield by runoff on loess slope[J]. Advances in Water Science,2006,17(4):444-449. (in Chinese)
15 ZHENG F L, HUANG C H, NORTON L D. Effects of near-surface hydraulic gradients on nitrate and phosphorus losses in surface runoff[J]. Journal of Environmental Quality, 2004, 33(6):2174-2182.
16 SIMON A, COLLISON A J C. Pore-water pressure effects on the detachment of cohesive stream beds: seepage forces and matric suction[J]. Earth Surface Processes and Landforms, 2001, 26(13): 1421-1442.
17 FOX G A, CHU-AGOR M L M, WILSON G V. Erosion of noncohesive sediment by ground water seepage: lysimeter experiments and stability modeling[J]. Soil Science Society of America Journal, 2007, 71(6): 1822-1830.
18 Al-MADHHACHI A S T, HANSON G J, FOX G A, et al. Deriving parameters of a fundamental detachment model for cohesive soils from flume and jet erosion tests[J]. Transactions of the ASABE, 2013, 56(2):489-504.
20 SEGHIR A, BENAMAR A, WANG H. Effects of fine particles on the suffusion of cohesionless soils experiments and modeling[J]. Transport in Porous Media, 2014, 103(2):233-247.
21 NOUWAKPO S K, HUANG C, BOWLING L, et al. Impact of vertical hydraulic gradient on rill erodibility and critical shear stress[J]. Soil Science Society of America Journal, 2010, 74(6): 1914-1921.
22 雷廷武, NEARING M A. 水流作用下疏松土壤材料中细沟的再生及其临界剪应力的实验研究[J]. 农业工程学报, 2000, 16(1):26-30. LEI Tingwu, NEARING M A. Laboratory experiments of rill initiation and critical shear stress in loose soil material[J]. Transactions of the CSAE, 2000, 16(1):26-30. (in Chinese)
23 刘武林,邓玉林,李春艳,等. 长江中上游土壤侵蚀预报模型研究进展[J]. 水土保持应用技术,2006(3):29-32.
24 FITZJOHN C, TERNAN J L,WILLIAMS A G. Soil moisture variability in a semi-arid gully catchment:implications for runoff erosion control[J].CATENA,1998,32(1): 55-70.
25 陈洪松,邵明安,王克林.土壤初始含水率对坡面降雨入渗及土壤水分再分布的影响[J].农业工程学报, 2006,22(1):44-47. CHEN Hongsong, SHAO Ming’an, WANG Kelin. Effects of initial water content on hillslope rainfall infiltration and soil water redistribution [J]. Transactions of the CSAE, 2006, 22(1): 44-47. (in Chinese)
26 MCDOWELL R W, SHARPLEY A N. The effect of antecedent moisture conditions on sediment and phosphorus loss during overland flow:Mahantango Creek catchment, Pennsylvanian, USA[J]. Hydrological Processes,2002,16(15):3037-3050.
27 张光辉,刘宝元,张科利. 坡面径流分离土壤的水动力学实验研究[J].土壤学报,2002,39(6):882-886. ZHANG Guanghui, LIU Baoyuan, ZHANG Keli. Experimental simulation of hydraulic mechanism of soil detachment by suface runoff on slopeland[J]. Acta Pedologica Sinica,2002,39(6):882-886. (in Chinese)
28 OWOPUTI L O, STOLTE W J. Soil detachment in the physically based soil erosion process: a review[J]. Transactions of the ASAE, 1995, 38(4):1099-1110.
29 张光辉, 刘宝元, 何小武. 黄土区原状土壤分离过程的水动力学机理研究[J]. 水土保持学报, 2005, 19(4):48-52. ZHANG Guanghui, LIU Baoyuan, HE Xiaowu. Study on hydro-dynamic mechanism of natural soil detachment in loess region[J]. Journal of Soil Water Conservation, 2005,19(4):48-52. (in Chinese)
30 KINNELL P I A. Raindrop-impact-induced erosion processes and prediction: a review[J]. Hydrological Processes, 2005, 19(14):2815-2844.
31 RAUWS G, COVERS G. Hydraulic and soil mechanical aspects of rill generation on agricultural soils[J]. European Journal of Soil Science, 1988, 39(1):111-124.
32 陆兆熊,MERZ W.应用盐液示踪技术测定表面流速[M]∥晋西黄土高原土壤侵蚀管理与地理信息系统应用研究.北京:科学出版社,1992.
33 刘振波, 史学正, 于东升,等. 模拟降雨下土壤前期含水量对土壤可蚀性的影响[J]. 生态环境, 2008, 17(1):397-402. LIU Zhenbo, SHI Xuezheng, YU Dongsheng,et al. Effect of antecedent soil moisture on soil erodibility using simulation rainfall[J]. Ecology and Environment, 2008, 17(1):397-402. (in Chinese)
34 田培,潘成忠,许新宜,等. 坡面流速及侵蚀产沙空间变异性试验[J]. 水科学进展,2015,26(2):178-186. TIAN Pei, PAN Chengzhong, XU Xinyi, et al. Field experiment investigation into the spatial variability of overland flow velocity and soil erosion[J]. Advances in Water Science, 2015,26(2):178-186. (in Chinese)
35 陈椿庭.关于明渠水流的六区流态[J].人民长江,1995,26(3):43-46.
36 张科利, 秋吉康宏. 坡面细沟侵蚀发生的临界水力条件研究[J]. 水土保持学报, 1998,4(1):41-46. ZHANG Keli, AKIYOSHI Yasuhiro. Critical hydraulic condition of rill erosion on sloping surface[J]. Journal of Soil and Water Conservation, 1998,4(1):41-46. (in Chinese)
37 ABRAHAMS A D, LI G, PARSONS A J. Rill hydraulics on a semiarid hillslope, southern Arizona[J]. Earth Surface Processes & Landforms, 1996, 21(1):35-47.
38 ABRAHAMS A D, PARSONS A J. Hydraulics of interrill overland flow on stone-covered desert surfaces[J]. CATENA, 1994, 23(1):111-140.
39 GILLEY J E, KOTTWITZ E R, SIMANTON J R. Hydraulic characteristics of rills [J]. Transactions of ASAE, 1990, 33(6): 1900-1906.
40 FOSTER G R, HUGGINS L F, MEYER L D. A laboratory study of rill hydraulics: I. velocity relationships[J]. Transactions of the ASAE, 1984, 27(3): 790-796.
Critical Hydraulic Characteristics of Yellow Soil Detachment under Different Antecedent Soil Moisture Contents and Slope Gradients
WANG Chenfeng1WANG Bin1,2WANG Yujie1,2WANG Yunqi1,2HU Bo1LI Shirong3
(1.SchoolofSoilandWaterConservation,BeijingForestryUniversity,Beijing100083,China2.ChongqingJinyunForestEcologicalStation,BeijingForestryUniversity,Beijing100083,China3.BeijingSoilandWaterConservationCenter,Beijing100036,China)
Critical hydraulic characteristics of soil detachability are essential factors for soil erosion predicting. There is still insufficient knowledge on key factors and governing mechanism of soil detachability, especially for various near-surface soil water conditions. The typical eroded yellow soil area in the upper and middle Yangtze River was taken as the research area. In order to illustrate the response of critical condition of soil detachment under different subsurface soil water conditions, scour flume was used to measure hydrodynamics parameters. Five antecedent soil moisture contents (5%~23%) and five slope gradients (1.0°~10.0°) were designed. Results showed that critical flow velocity, flow depth and flow pattern of soil detachment all showed power function decreasing trends with the increase of slope gradient and antecedent soil moisture content. When the slope gradient was smaller than 5.0°, critical hydrodynamics parameters of soil detachment were influenced by coupling effects of slope gradient and antecedent soil moisture content; otherwise, it would be mainly influenced by slope gradient. It was also proposed that the simplified power function equation could be used accurately when slope gradient was larger than 5.0°. Most of the flow patterns belonged to laminar flow and subcritical flow. The slope gradient and antecedent soil moisture content played an important role in the overland flow Darcy-Weisbach friction factor. When Reynolds number and critical discharge per unit width were increased, the Darcy-Weisbach friction factor was decreased as power function.
soil detachment; antecedent soil moisture content; slope gradient; critical hydraulic characteristics; yellow soil
10.6041/j.issn.1000-1298.2017.04.029
2016-06-21
2017-01-16
国家自然科学基金项目(41401299)
王晨沣(1991—),男,博士生,主要从事水土保持研究,E-mail: chenfengwangbjfu@163.com
王彬(1983—),男,讲师,博士,主要从事土壤侵蚀预报与土壤可蚀性研究,E-mail: wangbin1836@gmail.com
S157
A
1000-1298(2017)04-0224-09

