基于总体局域均值分解及稀疏表示分类的天然气管道泄漏孔径识别
孙洁娣 彭志涛 温江涛 王 飞
1.燕山大学信息科学与工程学院,秦皇岛,066004 2.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,066004 3.中国石油天然气管道通信电力工程有限公司,廊坊,065000
基于总体局域均值分解及稀疏表示分类的天然气管道泄漏孔径识别
孙洁娣1彭志涛1温江涛2王 飞3
1.燕山大学信息科学与工程学院,秦皇岛,066004 2.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,066004 3.中国石油天然气管道通信电力工程有限公司,廊坊,065000
针对天然气管道泄漏受孔径、传感器距离、管道内压力等多种因素影响,特征提取及识别算法较为复杂的问题,提出了基于总体局域均值分解-相对熵的特征提取算法并结合稀疏表示分类的泄漏孔径识别新方法。该方法采用总体局域均值分解方法对泄漏信号进行自适应分解,得到不同孔径泄漏信号的特征信息,并根据KL散度选择包含主要泄漏信息的PF分量,在此基础上提取多种时频特征参数,获取全面准确表征泄漏信号的特征向量;针对小样本复杂信号的分类,提出稀疏表示分类器实现泄漏孔径准确分类。该分类器采用过完备字典求得测试信号的最稀疏解,并以此解作为测试信号的稀疏重构系数,以获取测试信号在不同类别中的重构信号,最终通过判断测试信号与重构信号的残差值大小完成泄漏孔径分类。实验结果表明,所提出的算法比传统的SVM及BP分类算法识别准确率高。
泄漏孔径识别;总体局域均值分解(ELMD);KL散度;稀疏表示分类器;过完备字典
0 引言
天然气管道泄漏会造成严重后果,微小泄漏是燃气管道发生燃爆的主要诱因,泄漏孔径的不同直接与危险程度相关,当传感系统检测到管道发生泄漏后,尽快估计出不同泄漏孔径,是快速制定管道抢修计划、评估泄漏尺度的重要基础,对燃气管道的泄漏及识别具有重要意义。
天然气管道泄漏信号受压力、检测距离等多种因素影响,是一种较为复杂的非平稳信号,为区别不同孔径泄漏,研究准确的表征泄漏孔径的特征提取及分类方法尤为重要[1]。近年来,在泄漏信号处理方面,除传统的对泄漏信号进行分析的傅里叶变换、小波变换[2-3]等方法外,一些较新的方法,如经验模态分解(empirical mode decomposition, EMD)等也应用其中[4-6],但常用的方法在分析泄漏信号时都存在较大局限性,如傅里叶变换只能单独地反映信号在时域或者频域的局部信息;小波变换受小波基及分解尺度选择的影响,不能自适应地分解信号;EMD方法存在过包络、欠包络、端点效应等问题。局域均值分解 (local mean decomposition, LMD)方法是一种新的自适应时频分析方法,它能将一个多分量信号自适应地分解成多个调幅调频分量信号,具有较好的时频特征提取能力,其改进算法——总体局域均值分解(ensemble local mean decomposition, ELMD)克服了模态混叠现象,更适合分析复杂的泄漏信号。在泄漏孔径诊断方面,目前主要通过神经网络分类方法[7]或支持向量机[8]对处理后的泄漏信号进行分类。理论上神经网络分类方法只有当趋近无穷的训练样本时,其识别精确度才能得以保证,而实际采集泄漏信号的样本数量有限,导致神经网络识别泄漏孔径较为困难。基于统计学习理论的支持向量机方法在小样本上具有学习优势,且具有较好的泛化能力,但气体管道泄漏信号的复杂性决定了较大的VC(Vapnik-Chervonenkis)维才能准确地表示泄漏信息,削弱了支持向量机在小样本下的学习优势,因此,这两类常用的分类方法对燃气管道泄漏孔径识别的效果并不理想。稀疏表示分类方法(sparse representation for classification,SRC)[9]是近年来兴起的方法,它对大样本及小样本分类都具有较好的识别分辨率,对高维样本也有好的分类效果[10],且随着样本的增加,系数变得更加稀疏,此类方法对特征的选取影响也较小,这些特点为识别特征空间较大的特征向量奠定了理论基础。
本文将ELMD及稀疏表示分类器相结合,为解决泄漏孔径识别提供新方法。该方法先将复杂泄漏信号通过ELMD进行自适应分解,并根据KL散度选择主要PF分量,进一步计算各分量的有效特征参数并构成特征向量来表征不同的泄漏孔径信息;在此基础上构建基于稀疏表示的分类器,采用稀疏表示方法在超完备字典基础上求得测试样本在不同类别中的重构信号,通过计算测试样本及其重构信号的残差值实现泄漏孔径识别。
1 基于ELMD-KL的特征提取
天然气管道的泄漏信号构成较为复杂,LMD能够将泄漏信号自适应地分解为多个调幅调频信号,这些分量能完整地表示泄漏信号的时频分布,再提取含泄漏孔径信息较多的分量的特征值构成特征向量,有利于泄漏孔径的识别。
1.1 ELMD概述
LMD[11]将信号X(t)分解为k个PF分量Cp(t)和残余分量uk(t),可表示为
(1)
由于泄漏信号的间断性和不连续性,LMD分解过程中会出现模态混叠,即一个PF分量中含有不同尺度成分,或不同的PF分量中含有同一尺度成分。它将导致LMD分解后PF分量的瞬时频率物理意义不明确,针对此问题,本文采用ELMD方法对信号进行处理,它是一种改进的LMD方法[12]。ELMD的具体算法如下:
(1) 确定总体平均次数M及加入的白噪声幅值,设初始分解次数m=1。
(2) 在泄漏信号X(t)中加入确定幅值的白噪声nm(t),即
Xm(t)=X(t)+nm(t)
(2)
(3) 对信号Xm(t)进行m次LMD分解,获得多个PF分量Cn,m(n=1,2,…,N),Cn,m为第m次分解得到的第n个PF分量。
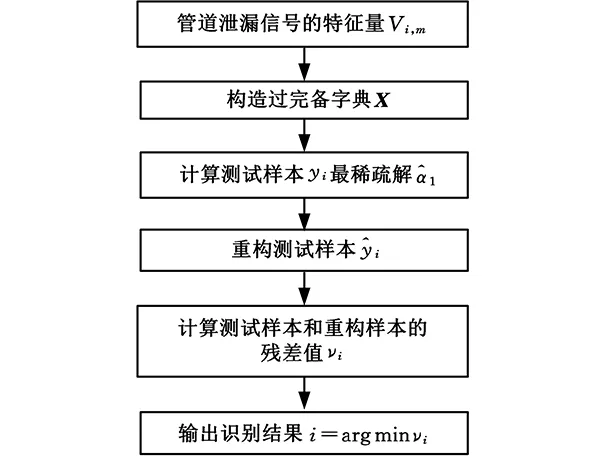
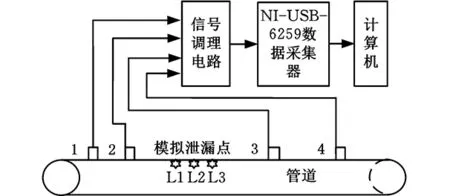
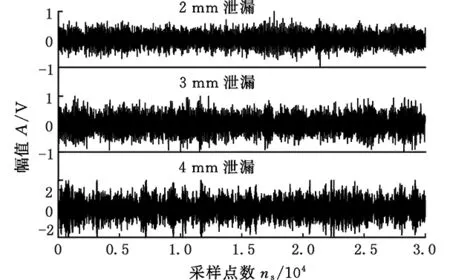
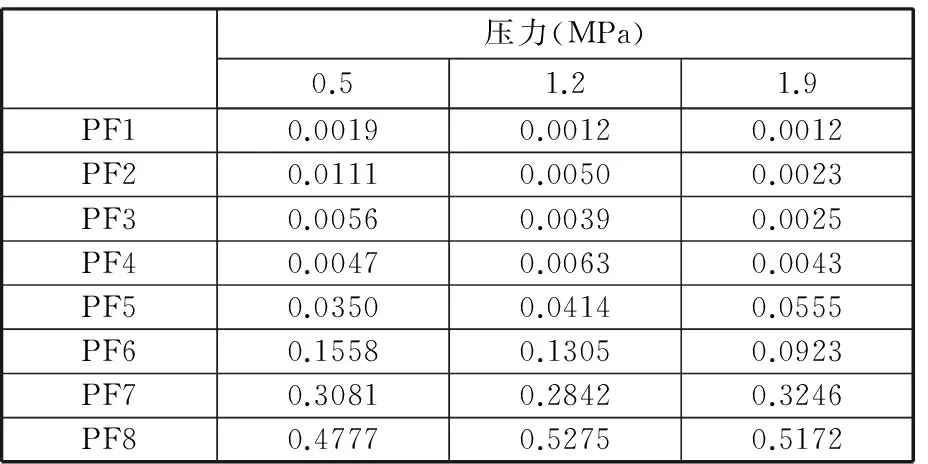
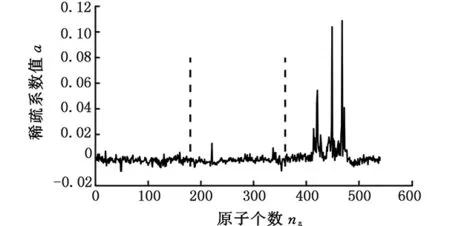
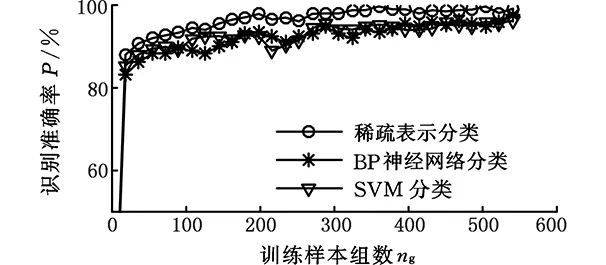
(4) 如果m (5)M次分解的PF分量的总体平均为 (3) n=1,2,…,Nm=1,2,…,M (6) 将N个PF分量M次分解的均值yn(n=1,2,…,N)作为最终的PF分量。 1.2 ELMD参数的确定 ELMD分解过程中,执行LMD分解的总次数M和噪声标准差决定了分解效果,两者关系如下: (4) 其中,ε为白噪声幅值标准差和输入信号标准差的比值系数;εn为期望的信号分解相对误差最大值。ε越小,信号分解精度越高,但ε太小,会降低ELMD分解的精确性;M过大,则会增加计算难度。理论及实验研究结果表明[13],ε的取值还受信号高频成分的幅值标准差影响,准确的参考值确定并不具有一般性。由于泄漏信号经LMD分解后,分量PF1含有效信号较多,故本文取其标准差为噪声标准差选择的参考值,经多次实验,在大多数情况下,当M=100、ε=0.01时,泄漏信号经过ELMD分解后,调幅调频信号分离效果较好,因此,在后续处理中M、ε取这两个值。 1.3 根据KL散度值选取主要PF分量 泄漏信号经过ELMD分解后得到若干个PF分量,研究结果表明,这些分量中故障信息含量差异较大,本文将泄漏信息含量较大的PF分量称为主要PF分量,其选取的准确性将直接影响特征提取及分类识别,本文在分析PF分量与泄漏信号关系的基础上,提出一种基于KL散度的主要PF分量选择方法。 由信息论可知,KL散度可以有效衡量两个信号的相似程度[14-15],散度值越小,两个信号的相似度越大;散度值越大,两个信号的相关程度越小。经ELMD分解后的PF分量,包含的故障信息越多,则PF分量与原信号的相似度越大;而包含噪声或其他成分的PF分量与原始信号相似度小,则散度值较大。因此,本文提出根据散度值大小选取主要PF分量,以降低其他PF分量对特征向量的影响。首先计算PF分量与原信号KL散度值,在进行散度值排序的基础上选取主要PF分量进行时频特征提取,算法处理步骤如下。 (1)对于信号x和信号y,采用非参数估计法计算概率分布,即 (5) 其中,k(·)表示核函数,本文采用高斯核函数,u为变量,有 (6) x的概率分布为p(x),同理,对信号y进行处理,求出概率分布为q(x),h为给定的正数。 (2) 依据两信号的概率分布,分别计算KL距离。信号x的KL距离为 (7) 同理,信号y的KL距离为δ(q,p)。 (3)计算两信号的KL散度值: D(p,q)=δ(q,p)+δ(p,q) (8) 式中,D(p,q)为两信号x和y的散度值。 比较每个PF分量与原信号的散度值大小,选取较小散度值对应的PF分量作为主要的分量,并对这些主要的PF分量进行分析,提取其含有的特征信息。 1.4 泄漏信号特征选取 天然气管道泄漏受多种因素影响,采用单一的特征无法全面有效地描述不同孔径泄漏,不易于准确识别。为此,本文在提取主要PF分量的基础上,分析泄漏信号的多个时频指标,并将其联合起来作为不同孔径泄漏的特征向量[16],主要包括反映泄漏信号时域离散程度及能量的标准差ST及有效值R;反映泄漏信号在频域变化的平均频率FM、中心频率FC和均方根频率FR;反映信号幅值变化的峰值系数F;反映信号波形的裕度参数C、偏度参数SF和形状参数S;反映信号尖峭程度的峭度系数K,将这些特征组合起来,能全面有效地反映泄漏信号的特征。限于篇幅,仅给出个别特征参数计算方法,见表1。表中,Ci(n) 表示各主要PF分量,σt为标准差。 表1 部分特征参数计算公式 根据上述选取的特征参数计算单个PF分量的特征值,将这些特征值组合成特征向量: Tk=(ST,R,F,K,S,FM,FC,FR,C,SF) (9) 式(9)仅为泄漏信号局部特征,为此求出所有主要PF分量的特征值,构造以下高维特征向量来表示泄漏信号: T=(T1,T2,…,Tk) (10) 根据式(10)构建的特征向量可准确、有效、全面地表示泄漏孔径信息,避免了直接利用泄漏信号进行分类识别的复杂性和繁琐性,提高了分类效率。本文在后续的泄漏孔径识别过程中提及的样本均为泄漏信号经过上述处理后的特征向量。 在ELMD-KL模型基础上提取的是泄漏信号的高维特征向量,对于小样本高维特征的分类问题,常用的分类器无法有效准确地进行识别,为此,本文在Wright提出的稀疏分类方法基础上,采用基于过完备字典稀疏表示的分类方法实现泄漏孔径的识别。该方法首先利用训练样本训练出过完备字典,利用该字典中最少的原子重构测试样本,根据测试样本及重构样本的残差值识别泄漏孔径。该方法的重构样本是在过完备字典基础上建立的,因此,该方法对训练样本的依赖弱于其他分类方法,且对样本的维数及数目要求也低于其他分类方法,对泄漏信号采集中由于受到环境、泄漏检测装置等因素影响而导致的采集信号缺失具有一定容错性,为此,本文将稀疏表示分类器引入复杂泄漏孔径识别中,以提高识别准确度。 稀疏表示分类关键是用字典中的原子稀疏表示测试样本。由于气体管道泄漏受压力、传感器距离等多种因素影响,为更准确地识别泄漏孔径提供一个广阔范围的生成元素,本文选用训练样本构建过完备字典。 假设管道泄漏孔径有k类,第i类孔径的第m个泄漏孔径训练样本可表示为Vi,m,则第i类孔径构成的样本矩阵为 Xi=[Vi,1Vi,2…Vi,m] (11) 其中,Xi∈Rn×m,Vi,m∈Rn,n为训练样本的维数(信号特征个数)。 假设y为第i类泄漏孔径的一组测试样本,y∈Rn,则y可以由第i类样本矩阵Xi表示为 y=αi,1Vi,1+αi,1Vi,1+…+αi,mVi,m (12) α=(αi,1,αi,1,…,αi,m) 其中,α为解向量,α∈Rm。在实际情况下,测试样本y的泄漏孔径大小是未知的,样本矩阵为 (13) 其中,样本矩阵X在稀疏表示中称为字典,X∈Rn×mk,字典中每一列称为原子。 此时,第i类的测试样本y用字典重构可表示为 y=Xα (14) α=(0,…,0,αi,1,…,αi,m,0,…,0)α∈Rm×k 由上式可知,同类孔径的原子对该类测试样本重构贡献率最大,其余类别原子的重构贡献率几乎为零。 (15) (16) 由于监测过程中,管道泄漏信号存在噪声,故式(16)可写成 (17) 其中,ξ代表重构的测试样本误差容忍极限。根据拉格朗日定理做正规化处理以解决最优化问题[18],即 (18) 式中,λ为正则化参数。 (19) 最后计算测试样本与每类重构样本的残差值: (20) 根据残差值的大小判断管道泄漏孔径的类别, 求νi的最小值,则表示该测试样本属于第i类泄漏孔径。即 i=arg minνii=1,2,…,k (21) 基于稀疏表示分类的管道泄漏孔径过程如图1所示。 图1 基于稀疏表示识别泄漏孔径的流程图Fig.1 Flowchart of gas pipeline leak recognition based on SRC 3.1 实验数据采集概述 为了验证本文方法,进行实地信号采集及处理。考虑到安全及成本问题,实验中用空气代替燃气,采用外径为108 mm、壁厚4.5 mm、长度为62 m的无缝钢管模拟输气管道,采用加速度传感器及数据采集电路,配合NI的数据采集卡USB-6259实现泄漏数据采集,每个通道的数据采集速率为100 kS/s。实验中的压力变化范围为0.5~2 MPa,通过减压阀放气,使管道内气体流动,管道内气体流速为3.1 m/s,实验管道上模拟泄漏孔径分别为2 mm、3 mm、4 mm,标记为L1、L2、L3,以球阀封堵。图2为天然气管道泄漏检测示意图,图中,1,2,3,4为4个压电振动传感器。 图2 实验中的泄漏信号采集系统结构简图Fig.2 Schematic of experiment system 根据泄漏信号的传播机理,按图3所示的方法安装压电传感器。 图3 实验现场压电传感器安装图Fig.3 Experimental schematic of piezoelectric sensor 实验过程中,传感器在0.5~2.0 MPa压力下分别对孔径2 mm、3 mm、4 mm泄漏产生的振动信号进行采样,每类孔径得到若干组数据。以1号传感器在2 MPa压力下各泄漏孔径的部分信号为例,如图4所示。 图4 不同泄漏孔径信号Fig.4 Leak signals of different apertures 3.2 泄漏信号特征提取 由前文可知,ELMD分解方法能将泄漏信号分解成若干个单分量信号,还能保存原信号的频率和幅值变换,对ELMD分解的主要PF分量进行特征提取,能更加全面准确地表示泄漏信号的特征信息。 以1号传感器在2 MPa压力下的2 mm泄漏孔径ELMD分解为例,对采集的泄漏信号进行ELMD分解,加入噪声幅值为信号标准差的0.015倍,总平均次数为100,泄漏信号分解结果如图5所示。其中,sPF1~sPF8分别为PF1~PF8的分量。 图5 2 mm泄漏信号ELMD分解结果Fig.5 ELMD results of 2 mm leak signal 泄漏信号经ELMD分解后,得到若干个PF分量,不同的PF分量包含特征信息不一致,根据1.4节方法,计算KL散度值并选取主要的PF分量。 1号传感器、泄漏孔径为2 mm、压力分别为0.5 MPa、1.2 MPa、1.9 MPa下泄漏信号PF分量的KL散度值见表2。泄漏孔径为2 mm、不同传感器、1.8 MPa压力下, 泄漏信号PF分量的KL散度值见表3。 表2 不同压力下的KL散度值 表3 不同传感器下的KL散度值 对比表2和表3发现,分量PF1、PF2、PF3、PF4的KL散度值都较小,其他PF分量的散度值较大,因此,泄漏信号经ELMD分解后得到的PF分量中,PF1、PF2、PF3、PF4包含泄漏信号大量的特征信息,其他PF分量几乎不含有效泄漏信息。故本文选取PF1、PF3、PF3、PF4作为主要PF分量。按前文所述,计算选取这4个主要PF分量的多个时频特征信息,得到共计40个特征参数,作为该泄漏信号的特征向量。 3.3 基于稀疏表示分类的泄漏孔径识别 实验数据选择压力间隔为0.2 MPa的三种泄漏孔径的10组数据,即每种泄漏孔径在不同压力、不同传感器下共得到240组样本数据。根据本文的特征提取方法求得每个泄漏信号的特征值,每类泄漏孔径选取180组作为训练样本,剩下60组作为该类测试样本。利用这些训练样本建立字典,求出测试信号在字典上的稀疏解。以2号传感器采集的1.8 MPa压力下的2 mm、3 mm、4 mm泄漏孔径测试样本中的一组样本为例,计算它们的稀疏解,图6所示分别为三种泄漏孔径的稀疏系数,图中两条竖虚线为每类原子在字典中的分割线。 由图6可知,泄漏孔径样本在字典同类别泄漏孔径原子中系数较大,与之不同类的泄漏孔径的稀疏系数趋近于零,可知测试样本被字典中同类的原子稀疏表示,能较好地逼近测试样本。计算每个测试样本在不同类中的系数,利用这些系数计算得到测试样本在该类的重构样本,将测试样本与重构样本的残差值作为测试样本分类的依据,限于篇幅,仅给出部分分类结果,见表4。 由表4可知,测试样本与重构样本的残差值最小,则测试样本属于该类别,笔者发现,由于泄漏信号受压力变化和泄漏点检测位置的影响,不同孔径的某些泄漏信号出现了相似性,稀疏表示分类器未能准确地识别泄漏孔径,例如表4中第67个测试样本,但总体结果表明,基于稀疏表示的分类器能够准确地识别泄漏孔径。 (a)2 mm泄漏孔径信号 (b)3 mm泄漏孔径信号 (c)4 mm泄漏孔径信号图6 不同泄漏孔径在各原子上的稀疏系数Fig.6 Sparse coefficients of different leak apertures in each atom 测试样本标签测试样本在不同泄漏孔径下的残差值孔径2mm孔径3mm孔径4mm孔径判别结果(mm)10.02470.24040.2126220.10341.33223.2513230.17072.55690.3833240.14420.97021.3991250.09711.11940.9938260.01140.73600.36342……………660.16930.07370.20353670.15780.16850.22872681.32500.79523.68073690.18380.02540.32663700.22410.09170.20063711.17930.02100.34143……………1400.73871.21320.101241411.05971.08200.035941420.99190.50080.119741431.53800.53650.024741440.63011.62860.029841451.84791.76510.12444…………… 为检验本文提出的稀疏分类器对泄漏孔径的识别效果,分别构建BP神经网络和支持向量机SVM分类模型,采用三种方法对测试样本分类,分类结果如图7所示。 图7 三种分类器对泄漏孔径分类对比Fig.7 Comparison of classification accuracy with three methods 对比图7中的三种分类器分类结果可知,稀疏表示分类效果优于BP神经网络和支持向量机识别结果。 本文算法对采集的泄漏信号出现一定程度缺损也能够取得较好的识别效果,下面给出一组数据缺损状态下稀疏表示分类器的分类结果。从1号、3号传感器采集的一段压力(压力以0.4 MPa为间隔)下分别取2 mm、3 mm、4 mm泄漏孔径10组数据,每类泄漏孔径100组数据,将这些数据全部作为训练样本,依然选用上次实验的测试样本作为测试样本,分类结果如图8所示。 图8 不同泄漏孔径分类结果Fig.8 Classification results of different leak apertures 观察图8可知,稀疏表示分类方法对管道泄漏孔径有较好的识别效果。训练信号经过稀疏表示分类能够较好地逼近测试信号。因此,稀疏表示分类方法对训练样本不敏感,均能有较高的识别精度。 图9 数据有损时三种分类器分类对比Fig.9 Comparison of three classifiers with damaged data 将上述实验样本分别作为BP神经网络和支持向量机分类器的输入向量,对比三种分类结果。分类结果如图9所示,由图9可知,对管道泄漏孔径识别的准确率从高到低依次为:稀疏表示分类、SVM分类、BP神经网络分类。 研究结果表明,基于稀疏表示分类器的识别准确率在管道泄漏孔径识别中较SVM及BP神经网络分类器更具有优势。由于泄漏信号非常复杂,机器学习过程中只有VC维越大,学习能力才越强,学习也就越复杂,这也导致SVM分类器的置信风险变大,分类效果受到影响。基于经验风险最小化的BP神经网络分类方法结构较为简单,在训练样本较少的情况下,不能保证理想的泛化能力,训练的识别率不高,分类效果不突出。本文提出的稀疏表示分类器主要依据与测试样本相似或相邻的样本重构,并利用其残差值进行泄漏孔径分类识别,稀疏重构系数经过一定量的样本的训练可以达到最佳稀疏表示,从而使重构结果与测试样本更为接近,即小样本训练就可以达到高效的稀疏表示,从而实现高精度分类。 ELMD-KL散度方法可以分解复杂泄漏信号,提取主要PF分量,进而获取泄漏信号的有效时频域特征,充分表征不同孔径的泄漏信息。针对提取的高维特征信息,提出了基于稀疏表示的分类方法,该方法对特征参数的选取及采集条件、样本数量等依赖性较小,对小样本的泄漏孔径识别具有比BP及SVM更好的识别效果。实验结果表明,本文方法具有较好的分类效果。 [1] 孙洁娣, 肖启阳, 温江涛,等. 局域均值分解分析的管道泄漏孔径识别及定位[J]. 仪器仪表学报, 2014(12):2835-2842. SUN Jiedi, XIAO Qiyang, WEN Jiangtao,et al. Pipieline Leak Aperture Classification and Location Based on Local Mean Decomposition Analysis[J].Chinese Journal of Scientific Instrument,2014(12):2835-2842. [2] 张景川, 曾周末, 赖平, 等. 基于小波能谱和小波信息熵的管道异常振动事件识别方法[J]. 振动与冲击,2010,29(5):1-4. ZHANG Jingchuan, ZENG Zhoumo,LAI Ping,et al. A Recognition Method with Wavelet Energy Spectrum and Wavelet Information Entropy for Abnormal Vibration Events of a Petroleum Pipeline[J]. Journal of Vibration and Shock,2010,29(5):1-4. [3] 孙洁娣, 靳世久. 基于小波包能量及高阶谱的特征提取方法[J]. 天津大学学报,2010,43(6):562-566. SUN Jiedi, JIN Shijiu. Feature Extraction Method Based on Wavelet Packet Energy and High-order Spectrum [J]. Journal of Tianjin University,2010,43(6):562-566. [4] 程军圣, 张亢, 杨宇, 等. 局部均值分解与经验模式分解的对比研究[J]. 振动与冲击, 2009, 28(5): 13-16. CHENG Junsheng, ZHANG Kang, YANG Yu, et al. Comparison between the Methods of Local Mean Decomposition and Empirical Mode Decomposition[J]. Journal of Vibration and Shock,2009,28(5):13-16. [5] 王建国, 吴林峰, 秦绪华. 基于自相关分析和LMD的滚动轴承振动信号故障特征提取[J].中国机械工程,2014,25(2):186-191. WANG Jianguo, WU Linfeng, QIN Xuhua. Rolling Bearing Vibration Signal Fault Feature Extraction Based on Autocorrelation Analysis and LMD [J]. China Mechanical Engineering,2014,25(2):186-191. [6] SUN Jiedi, XIAO Qiyang, WEN Jiangtao, et al. Natural Gas Pipeline Small Leakage Feature Extraction and Recognition Based on LMD Envelope Spectrum Entropy and SVM [J]. Measurement,2014,55:434-443. [7] JOSHI A, UDPA L, UDPA S, et al. Adaptive Wavelets for Characterizing Magnetic Flux Leakage Signals from Pipeline Inspection[J].IEEE Transactions on Magnetics,2006,42(10):3168-3170. [8] 王明达, 张来斌, 梁伟, 等. 基于独立分量分析和支持向量机的管道泄漏识别方法[J]. 石油学报, 2010, 31(4): 659-663. WANG Mingda, ZHANG Laibin, LIANG Wei, et al. Pipeline Leakage Detection Method Based on Independent Component Analysis and Support Vector Machine[J].Acta Petrolei Sinica,2010,31(4):659-663. [9] WRIGHT J, YANG A Y, GANESH A, et al. Robust Face Recognition via Sparse Representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227. [10] 朱启兵, 杨宝, 黄敏. 基于核映射稀疏表示分类的轴承故障诊断[J]. 振动与冲击,2013,32(11):30-34. ZHU Qibing, YANG Bao, HUANG Min.Bearing Fault Diagnosis Based on a Kernel-mapping Sparse Representation Classification[J].Journal of Vibration and Shock,2013,32(11):30-34. [11] SMITH J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface,2005,2(5):443-454. [12] 孙洁娣, 肖启阳, 温江涛,等. 改进LMD及高阶模糊度函数的管道泄漏定位[J]. 仪器仪表学报, 2015, 36(10): 2215-2223. SUN Jiedi, XIAO Qiyang, WEN Jiangtao, et al. Pipeline Leakage Localization Based on ELMD and High-order Ambiguity Function [J]. Chinese Journal of Scientific Instrument,2015,36(10):2215-2223. [13] 王建国, 陈帅, 张超. 噪声参数最优ELMD与LS-SVM在轴承故障诊断中的应用与研究[J]. 振动与冲击, 2017, 36(5):72-78. WANG Jianguo, CHEN Shuai, ZHANG Chao. Application and Research of Optimal Noise Parameters Ensemble Local Mean Decomposition and LS-SVM in Bearing Fault Diagnosis [J]. Journal of Vibration and Shock,2017,36(5):72-78. [14] 何志坚, 周志雄. 基于ELMD的样本熵及Boosting-SVM的滚动轴承故障诊断[J].振动与冲击, 2016, 35(18):190-195. HE Zhijian, ZHOU Zhixiong. Fault Diagnosis of Roller Bearings Based on ELMD Sample Entropy and Boosting-SVM [J]. Journal of Vibration and Shock,2016,35(18):190-195. [15] 韩中合, 朱霄珣, 李文华. 基于KL散度的EMD虚假分量识别方法研究[J]. 中国电机工程学报, 2012, 32(11): 112-117. HAN Zhonghe, ZHU Xiaoxun, LI Wenhua. A False Component Identification Method of EMD Based on Kullbackleibler Divergence[J]. Proceedings of the CSEE,2012,32(11):112-117. [16] LIU Z, CAO H, CHEN X, et al. Multi-fault Classification Based on Wavelet SVM with PSO Algorithm to Analyze Vibration Signals from Rolling Element Bearings[J]. Neurocomputing,2013,99(1):399-410. [17] DONOHO D L. Compressed Sensing [J]. IEEE Transactions on Information Theory, 2006,52(4):1289-1306. [18] YANG J, ZHANG D, YANG J Y. Face Recognition Using Laplacian Faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(4):650-664. (编辑 陈 勇) Natural Gas Pipeline Leakage Aperture Identification Based on ELMD and SRC SUN Jiedi1PENG Zhitao1WEN Jiangtao2WANG Fei3 1.School of Information Science and Engineering, Yanshan University,Qinhuangdao,Hebei,0660042.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province,Yanshan University, Qinhuangdao,Hebei,0660043.China Petroleum and Gas Pipeline Telecommunication and Electricity Engineering Corporation, Langfang,Hebei,065000 Natural gas pipeline leakage was influenced by the aperture, the sensor distance, the pressures in the pipeline and many factors, so the feature extraction and recognition algorithm is relatively complicated. A novel leak aperture identification method which combined feature extraction based on ELMD-KL model with SRC was proposed. ELMD was applied to adaptively decompose leak signals, to obtain characteristic informations of different aperture leak signals, and to extract the principal product function(PF) components based on KL divergence which contained the main leakage informations. The method extracted multiple characteristic parameters in time domain and frequency domain as the feature vectors. For the classification of small sample complex signals, a SRC was put forward to realize the accurate classification of leak apertures. The classifier obtained the most sparse solutions of the test signals with overcomplete dictionary. The solutions were used as the sparse coefficient to reconstruct the test signals and obtain reconstruction signals in different classes of the test signals. Finally, classification of leak apertures was accomplished by judging the residual values between test signals and reconstruction signals. The experimental results show that the proposed algorithm has higher recognition accuracy compared with the traditional classification algorithm of SVM and BP. leakage aperture identification; ensemble local mean decomposition (ELMD); KL divergence; sparse representation classifier(SRC); overcomplete dictionary 2016-06-23 国家自然科学基金资助项目(51204145);河北省自然科学基金资助项目(E2013203300, E2016203223) TH865;TH213.3 10.3969/j.issn.1004-132X.2017.10.011 孙洁娣,女,1975年生。燕山大学信息科学与工程学院副教授、博士。主要研究方向为压缩感知及盲信号处理理论及应用、复杂振动信号处理、油气管道泄漏检测。发表论文30余篇。E-mail: wjtsjd@163.com。彭志涛,男,1990年生。燕山大学信息科学与工程学院硕士。温江涛,男,1974年生。燕山大学电气工程学院副教授、博士。王 飞,男,1978年生。中国石油天然气管道通信电力工程有限公司高级工程师。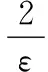


2 基于稀疏表示分类的泄漏孔径识别
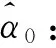
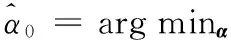
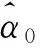
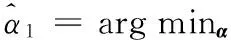
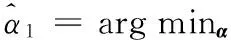


3 实验数据采集与处理







4 结论

