基于几何特征的整体叶轮三维测量模型与CAD模型对齐方法
邢晓红 郭明森 黄金昌
1.南京航空航天大学金城学院机电工程系,南京,211156 2.南京航空航天大学精密驱动研究所,南京,210016 3.沈阳飞机设计研究所,沈阳,110035
基于几何特征的整体叶轮三维测量模型与CAD模型对齐方法
邢晓红1郭明森2黄金昌3
1.南京航空航天大学金城学院机电工程系,南京,211156 2.南京航空航天大学精密驱动研究所,南京,210016 3.沈阳飞机设计研究所,沈阳,110035
提出了基于几何特征的模型对齐方法,并应用于整体叶轮三维模型。提取了测量模型的质心。根据整体叶轮对称性,采用最小二乘法对其轴线进行了估算,并采用加工精度高的轴位置数据对轴线进行了修正,从而将测量模型的质心、轴线与CAD模型的质心及轴线对齐。根据整体叶轮的制造精度特征,采用加权最小二乘法,实现了叶片区域测量模型与CAD模型的对齐。经计算,采用上述方法的最大对齐误差为0.2 mm。
整体叶轮;几何特征;三维测量;对齐
0 引言
整体叶轮是透平机械的核心,也是各类航空发动机的关键部件,已经广泛地用于航空、航天及其他工业领域。目前整体叶轮加工一般采用铸造加工、电火花加工、电解加工及数控铣削加工等方法。数控加工柔性好,可加工复杂形状叶轮,且表面质量好、效率高、适用广泛,因此五坐标数控铣削加工也是整体叶轮加工常采用的方法之一[1-2]。
数控加工后的检测是必不可少的步骤,检测结果可以帮助工艺人员和数控编程人员发现存在的问题,并针对问题提出适当的解决办法。就整体叶轮的测量方法而言,目前主要有三种方法,即型面样板检测法、三坐标测量机检测法以及光学检测法。整体叶轮叶片型面测量的趋势是使用光学检测法。在测量效率上,采用光学检测法的测量速度要比型面样板以及三坐标方法高数个数量级,并且能够覆盖被测零件的大部分表面甚至全部表面,且该方法对环境要求小,适用于现场测量。
对于光学检测法,在对测量数据进行分析前,需要将测量坐标系与建模坐标系对齐。在测量过程中其测量坐标系是根据测量仪器自身系统建立的,这个坐标系与建模坐标系一般不会一致,因此需要在测得数据后进行对齐操作。文献[3-4]研究了单个叶片的对齐及测量分析方法。然而对于整体叶轮三维测量模型与CAD模型的对齐方法研究还未有文献报道。
在对光学测量仪测得的整体叶轮点云数据模型进行坐标对齐操作的过程中,由于叶轮上带有孔的内表面很难测得,且整体叶轮类零件属于轴对称,因此难以确定其测量坐标系。本文提出了一套整体叶轮测量坐标系与建模坐标系对齐方法。
1 整体叶轮对齐方法
图1所示为采用ATOS光学测量仪器测得的STL数据模型。整体叶轮零件对齐过程即通过调整其6个自由度(3个平移自由度和3个旋转自由度),通过某种算法将测量模型与原始CAD模型进行对齐。这个过程与经典的最近点迭代(iterative closest point,ICP)方法的思想是一致的[5]。传统的最近点迭代方法对测量数据进行配准定位计算时,根据测量数据在CAD模型表面求取最近点集,再进行变换迭代。

图1 整体叶轮测量数据模型Fig.1 Measured data model of integral impeller
整体叶轮不同于自由曲面零件,该类零件具有明显的设计特征,即整体叶轮是一个典型的绕轴旋转工作零件,因此,对其轴线的估计是模型对齐的基础。根据测量数据点到对称轴线距离的平方和为最小来对轴线进行估算。将质心位置移动到建模坐标系下模型质心位置,并使其轴线对齐。此时,测量数据限制了沿X、Y、Z轴的平动以及绕X、Y轴的转动。余下一个自由度,即绕Z轴的转动自由度需要确定。在这个自由度(绕Z轴的旋转)的对齐问题上,本文直接采用测量模型与CAD模型进行对齐,并且针对叶片存在的变形问题,提出一种加权最小二乘对齐方法。
2 具体算法及流程
2.1 质心
设STL模型中的数据点为pi=(xi,yi,zi),i=1,2,…,n,则该模型的质心可估算为[6]
(1)
绝对均匀的整体叶轮零件的质心应位于其轴线上。质心估计的意义在于可以为其轴线的计算提供基础。
2.2 旋转轴线
本文利用各点到轴线距离平方和最小这个特点,采用最小二乘方法对模型轴线进行估计。
图2所示为空间点和一条空间直线。po为直线上一点,也就是式(1)中的质心。设该直线方向矢量为v,并设其为单位矢量,即|v|=1;pi为直线外一点,计算点pi到直线的距离di的标准公式为
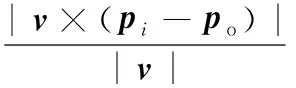
(2)

图2 空间点到直线的距离Fig.2 The distance between a point and a line
由于|v|=1,则式(2)可简化为
di=|v×(pi-po)|
(3)
根据向量的向量积性质,式(3)可以继续简化为
di=|v||pi-po|sinθ=|pi-po|sinθ
(4)
设v=(α,β,γ),其中α2+β2+γ2=1,po=(xo,yo,zo),取测量数据点到轴线距离的平方和为目标函数,并计算其极小值,即有
(5)
分别对α,β,γ求偏导,并令其为0,则可得以下方程组:

方程组系数矩阵为一对称矩阵。在求解过程中不需要计算出具体的数值,只需要得到α/β以及β/γ即可。
通过以上方法可估算出轴对称零件的轴线。若测量数据足够均匀,则该方法可以得到近似程度较高的结果。图3中的理想模型来自UG软件。
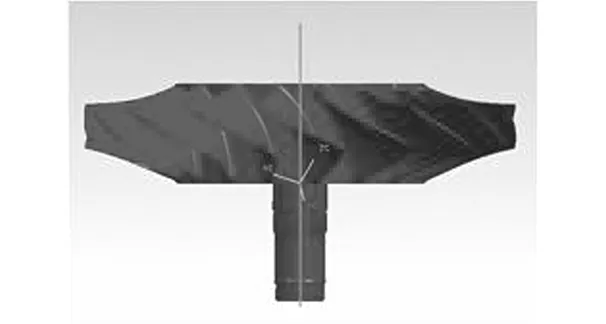
图3 理想模型旋转轴最小二乘估计Fig.3 Therotational axis estimated by least square algorithm from ideal model
2.3 旋转轴位置修正
由于在测量过程中存在测量仪器的误差以及测量盲区等问题,往往所采集的点云数据并不十分均匀,因此通过2.2节方法所得到的结果并不一定能令人满意,只能实现大致的对齐,如图4所示。
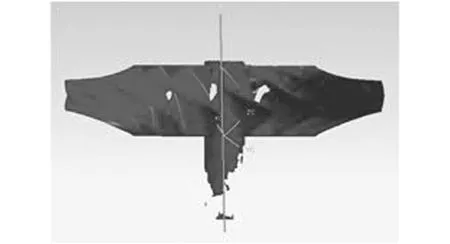
图4 测量模型旋转轴最小二乘估计Fig.4 The rotational axis estimated by least square algorithm from measured model
由图3、图4可以明显看出,计算得到的轴线与所测数据模型的实际轴线存在一定偏差,这需要对该轴线进行修正。本文针对整体叶轮的制造特征提出了精确轴线提取方法。
整体叶轮类零件是一类旋转工作零件,因此在制造过程中对整体叶轮的旋转轴有着极高的精度要求,轴在装配过程中起着重要的定位作用。因此,可提取测量模型轴位置数据作为叶轮旋转轴线精确估计的依据。
为简化该问题,将上一节中得到的轴线通过旋转操作使其与Z轴重合。垂直于该轴线(即Z轴)建立截平面,得到该平面与轴位置测量数据模型的交点。通常情况下,该截面是一个椭圆。
本文通过截取数个轴位置截面数据,计算每个截面数据的中心,并将所有中心点数据拟合成一条直线,即为轴线的精确估计。同时,该轴线应通过CAD模型的质心以及CAD模型所在坐标系的原点。考虑到对椭圆拟合比较复杂,而根据椭圆的对称性可知,采用圆对其进行拟合即可。拟合方法如下[7]:
只考虑数据点在OXY平面上的投影,设该组数据点为(xj,yj)。设假想的圆心坐标为(xc,yc),圆的半径为R,则与该组数据点的距离平方和为最小的圆的方程为
(x-xc)2+(y-yc)2=R2
建立目标函数如下:
为避免求导的复杂,上式中没有采用距离的平方和最小为目标函数。计算该函数的极小值,便可得到三个未知量,如图5所示。

图5 椭圆的圆弧拟合Fig.5 Arc fitting of an ellipse
沿Z轴方向截取叶轮测量模型轴上m个截面数据,并采用上述方法对每个截面数据进行拟合,得到m个圆心位置,采用直线对这m个圆心位置进行拟合,拟合后的直线可作为修正后的整体叶轮测量数据模型的旋转轴线,如图6所示。
2.4 叶片曲面的对齐
通常在对整体叶轮的叶片型面检测过程中,并不需要对整个叶片型面的数据点进行检验,而只检验设定好的几个截面,因此可根据测量叶片型面与CAD叶片型面相对应截面数据之间的关系来进行对齐工作。由此可知,仍可采用经典的最小二乘法进行对齐。

(a)椭圆中心直线拟合

(b)修正后的测量模型轴线图6 测量模型轴线修正Fig.6 Modification of measured model axis
由经验可知,叶片在加工过程中一般存在变形,且变形量从叶尖到叶根逐渐减小。传统的最小二乘法是使测量数据点与叶片型面距离的平方和最小,却不一定符合实际情况。在对齐过程中,各个截面所需考虑的精度不同,即每个截面数据在对齐过程中所占的权重不同。
基于以上分析,本文采用加权最小二乘法对叶片型面进行匹配。
2.4.1 截面数据的选取
叶片的设计数据是由垂直于某个坐标轴的数个截面数据点定义的。当叶轮测量模型与CAD模型完全重合时,其中有一个叶片的测量模型与最原始的设计叶片重合,此时可以基于原始的截面定义位置,截取该叶片测量模型相应位置上的数据作为对齐数据依据。然而由分析可知,在叶片对齐之前,叶片部分的数据模型与CAD模型一般是不重合的,以这种方法得不到所需数据。由此,本文采用的方法是绕叶轮旋转轴线并以各个设计截面位置高度为半径作一系列的圆柱面,取得该圆柱面与测量模型的交点,以这些点作为依据,进行对齐工作。图7所示为一组叶片截面数据。

图7 一组叶片截面数据示意图Fig.7 Schematic of cross section data of blade
2.4.2 权值的确定以及目标函数的建立
在整体叶轮设计过程中,对叶片型面有公差要求,即需给出最大叶型偏差允许值。叶片出现最大叶型偏差的位置应位于其叶尖处,而叶片与轮毂的交线处的偏差最小,可认为没有偏差。
设存在p组截面,各组截面数据的权值计算如下:
计算各组截面与轮毂曲面之间的距离sk(1≤k≤p),其中最大距离为smax;计算每个截面到轮毂的距离与最大距离的比值为sk/smax;则本文取每个截面的权值λk=smax/sk,表示在匹配过程中,越靠近轮毂截面的数据越受重视,越应该靠近设计叶片型面。
得到权值后,建立基于加权最小二乘的目标函数:
其中,q代表每组截面具有q个数据点;dkl表示第k组截面上的第l个数据点与CAD模型叶片相应截面上最近点之间的距离,可通过UG/Open API提供的函数得到。
对该目标函数进行求解,其中距离可看作旋转角度的函数,求解出目标函数最小值对应的旋转角度。将测量模型数据根据该角度旋转,便可实现与CAD模型的对齐。
2.5 对齐结果
CAD模型与测量模型对齐结果如图8所示。采用ATOS软件自带手动对齐方法,得到测量模型与设计模型的最大对齐误差为0.5mm,而采用本文方法所得到的最大对齐误差为0.2mm。

图8 CAD模型与测量模型对齐结果Fig.8 Result of aligning measured model with CAD model
3 结论
本文提出了基于几何特征的三维测量模型与CAD模型对齐方法,并将此方法应用于整体叶轮的三维模型中。经计算,采用本文方法得到的最大对齐误差为0.2mm。
[1] 陈晧晖,刘华明,李刚,等. 复杂曲面叶轮CAD/CAM一体化系统开发[J]. 航天制造技术,2003(2):28-31.CHENHaohui,LIUHuaming,LIGang,etal.DevelopmentofCAD/CAMIntegralSystemforComplexCurvedImpeller[J].AerospaceManufacturingTechnology, 2003(2):28-31.
[2] 吴宝海,王尚锦. 自由曲面叶轮的四坐标数控加工研究[J]. 航空学报,2007,28(4):993-998.WUBaohai,WANGShangjin.Researchon4-axisNumericalControlMachiningofFree-formSurfaceImpellers[J].ActaAeronauticaetAstronauticaSinica, 2007, 28(4):993-998.
[3] 吕彦明,滕树新. 汽轮机叶片截型测量数据的自动分析[J]. 工具技术,2007,41(7):94-95.LYUYanming,TENGShuxin.AutomaticAnalysisofMeasuringDataofSectionalProfileonTurbineBlade[J].ToolEngineering, 2007,41(7):94-95.
[4] 陈福兴. 基于UG叶片型面测量分析技术的研究[D]. 无锡:江南大学,2006.CHENFuxing.ResearchonMeasurementandAnalysisTechnologyofBlade’sSurface[D].Wuxi:JiangnanUniversity, 2006.
[5]BESLPJ,MCKAYND.AMethodforRegistrationof3-DShapes[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1992,14(2):239-256.
[6] 王坚. 非规则碎片拼合关键技术研究[D]. 南京:南京航空航天大学,2007.WANGJian.ResearchonKeyTechnologyofIrregularFragmentsReassembly[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics, 2007.
[7] 雷家勇,达飞鹏,孟广猛. 图像处理中圆心算法研究[J]. 计算机与现代化,2005(3):25-26.LEIJiayong,DAFeipeng,MENGGuangmeng.ArithmeticofComputingCenterofCircleinComputerImageProcessing[J].ComputerandModernization, 2005(3):25-26.
(编辑 王旻玥)
An Aligning Method for 3D Measured Model with CAD Model of Integral Impeller Based on Geometric Features
XING Xiaohong1GUO Mingsen2HUANG Jinchang3
1.Mechanical and Electronic Engineering Department,NanHang Jincheng College,Nanjing,211156 2.Laboratory of Precision Drive,Nanjing University of Aeronautics and Astronautics,Nanjing,210016 3.Shenyang Aircraft Design and Research Institute,Shenyang,110035
A model alignment method was proposed based on geometric features, and applied to a 3D model of integral impellers. First, centroid of the measured models was extracted. According to the symmetry features of the integral impeller, the least square algorithm was utilized to estimate the rotational axis and was modified by the more accurate data of shaft part. Therefore, the centroids and rotational axes of the measured models were aligned with those of the CAD models. Then, the aligning of the blade parts of the measured models with the CAD models was realized by using weighted least squares method according to the characteristics of manufacture precision. The maximum alignment deviation caused by the proposed method is as 0.2 mm.
integral impeller; geometric feature; 3D measurement; alignment
2016-07-11
江苏省大学生创新创业训练计划项目(201613655016X)
TG806
10.3969/j.issn.1004-132X.2017.10.012
邢晓红,女,1980年生。南京航空航天大学金城学院机电工程系讲师。主要研究方向为数控加工技术和模具设计及制造。E-mail:xingxh@nuaa.edu.cn。郭明森,男,1980年生。南京航空航天大学航空宇航学院副教授、博士。黄金昌,男,1980年生。沈阳飞机设计研究所高级工程师。

