基于高温蠕变特性的连铸坯新矫直技术
张兴中 郭 龙 冯常喜
燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
基于高温蠕变特性的连铸坯新矫直技术
张兴中 郭 龙 冯常喜
燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
基于目前工厂常用的连铸坯矫直技术,考虑连铸坯在高温下的蠕变特性,提出利用高温蠕变对连铸坯进行蠕变矫直的新观点。针对某钢厂R9300连铸机设计了一条新型的曲率变化满足正弦规律且弯曲段和矫直段弧长显著延长的矫直曲线,通过数值模拟计算和对比分析,新矫直曲线的应变速率更低,矫直过程中可以充分利用材料的高温蠕变性能。通过在Gleeble-3800型热/力模拟试验机上对Q460E钢进行热塑性试验和蠕变拉伸试验,确定了该钢种的相关热物性参数和蠕变本构方程。由于新曲线矫直区的应变速率接近最小蠕变应变速率,连铸坯主要依靠高温蠕变变形进行矫直,降低了应变速率,可以避免连铸坯内部裂纹缺陷,有利于提高连铸坯的质量。
连铸坯;蠕变矫直;应变速率;矫直曲线
0 引言
连续铸钢是钢铁生产流程中的重要组成部分。进入21世纪以后,世界钢铁行业连铸比超过90%[1],2004年以后我国钢铁行业的连铸比超过96%[2]。连铸坯的内部裂纹是连铸生产过程中的主要缺陷,它不仅影响到连铸坯的质量还影响到后续的轧制过程[3]。连铸坯在弯曲矫直过程中处于800~1400 ℃的高温,而且受力复杂,很容易在内部和固液交界面产生裂纹[4]。由于金属在温度高于自身熔点温度的0.3倍时蠕变现象十分明显,因此连铸坯在弯曲矫直过程中具有明显的蠕变行为。
早期研究中,GRILL等[5]采用弹性和蠕变模型来预测连铸坯的鼓肚变形。OKAMURA等[6]采用弹-塑性和蠕变有限元方法研究了蠕变对连铸坯鼓肚变形的影响。 近年来, HUESPE等[7]采用弹-黏-塑性模型研究了圆形连铸坯的蠕变性能,并分析了其在整个连铸过程的应力状态。满媛等[8-9]对连铸坯在连续矫直过程中的高温蠕变行为做了大量的工作,并且提出了具有两个连续矫直区的新机型曲线。马春武等[10]对广泛使用的三次连续矫直曲线进行了应力应变分析,认为连铸坯在一定外力作用下会发生明显的蠕变行为。景奉儒等[11]对直弧型板坯连铸机连续弯曲矫直曲线进行了优化,提出弯曲与矫直应采用不同的应变速率来适应金属温度高、蠕变快的规律。这些学者都认为连铸坯在弯曲矫直变形过程中,要充分考虑蠕变的影响。黄文等[12]对多点矫直直弧型连铸机的矫直反力进行了计算。李宁[13]对薄板坯连铸机连续矫直区的矫直力和力矩的计算方法进行了研究。
这些研究都表明连铸坯在矫直变形时矫直力必须大于屈服强度,并没有充分考虑金属的高温蠕变特性。由于金属在高温低于屈服强度的应力作用下也会发生较快的永久变形,因此本文提出利用材料的这一高温蠕变特性,使连铸坯在弯曲矫直变形过程中主要依靠蠕变变形,降低连铸坯的矫直应力,避免内部裂纹的发生,从而提高连铸坯的质量。
1 理论基础
根据平截面假设,铸坯中性层在弯曲矫直过程中不发生伸长或缩短,因此连铸坯表面下某一层的弯曲矫直应变可以表示为

(1)
式中,εh为连铸坯某一层的应变;D为连铸坯厚度,mm;h为连铸坯某一层到中距离厚度,mm;ki为连铸坯在弯曲矫直开始点曲率,mm-1;ki+1为弯曲矫直结束点曲率,mm-1;i为弯曲矫直点序号。
由式(1)可以看出,连铸机机型曲线的曲率直接影响连铸坯的变形,由于圆弧曲率恒定,因此连铸坯在基本圆弧段时并不发生变形。目前工厂常用的各种连铸机机型都存在很长的基本圆弧段,因此缩短基本圆弧段长度,延长弯曲矫直段长度,可以增加连铸坯蠕变时间,发生更多的蠕变变形。由于多点矫直技术的多段圆弧连接点存在曲率突变,使连铸坯在每个矫直点产生应变突变,而连续矫直技术的曲率变化是连续的,因此将式(1)对时间进行求导,得到应变速率与曲率相对于弧长变化率的关系:
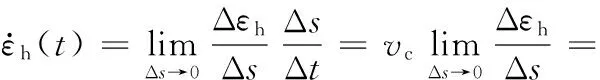
(2)
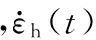
由式(2)可知,连铸机机型曲线的曲率变化率越小,连铸坯在弯曲矫直变形过程的应变速率越小,因此,选取一条合适的连铸机机型曲线,使其具有较小的曲率变化率和较长的弯曲和矫直弧长,可以增加连铸坯在弯曲矫直过程中蠕变的时间,发生更多的蠕变变形,并且使连铸坯在弯曲矫直段的应变速率更小。当应变速率小于屈服应力作用下的蠕变应变速率时,此时连铸坯的弯曲矫直变形过程中只存在蠕变变形,没有塑性变形。
2 机型曲线设计
本文以具有代表性的板坯直弧型连铸机为例,讨论蠕变矫直曲线的设计方法。连铸坯在弯曲过程中,曲线的曲率必须由0单调增至1/R,然后是一段半径为R的基本圆弧段,在矫直过程中,曲线的曲率必须由1/R单调减小至0。根据这些边界条件构造一条曲率满足正弦规律,曲率变化率满足余弦规律的机型曲线,其曲率和曲率变化率的表达式如下:

(3)

(4)
0≤s≤L
式中,R为连铸机基本圆弧半径,mm;L为弯曲段或矫直段总弧长,mm。
根据弧微分公式,曲线转角与弧长的关系可以表示为
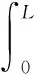
(5)
式中,α为曲线转角,rad。
直角坐标系下的横纵坐标与转角可以表示为
(6)
因此,该曲线在直角坐标系下的参数方程如下:
(7)
由式(7)可知,当基本圆弧半径和弯曲、矫直段总弧长确定时,该曲线唯一确定。该曲线的弯曲段与矫直段分别选择不同的曲线起始点,在弯曲起始点处s1为0时,曲率k1为0,与垂直段相切;在弯曲结束点处s1为L时,曲率k1为1/R,与基本圆弧段相切。同理在矫直段,起始点处s2为0时,曲率k1为0,与水平段相切;在矫直结束点处s2为L时,曲率k2为1/R,与基本圆弧段相切。通过平移和旋转坐标系,整条曲线可以光滑连接。
3 曲线实例计算
3.1 曲线参数计算
以某钢铁厂R9300五点弯曲五点矫直直弧型板坯连铸机为例,该机型曲线的参数见表1。

表1 R9300机型曲线参数
连铸机最小圆弧半径的取值与连铸坯断面形状和浇注的钢种有关。基本圆弧半径的计算公式如下:

(8)
式中,D为最大铸坯的厚度,mm;ε为连铸坯内弧表面允许应变值,一般ε取1.5%~2.0%。
针对某钢厂R9300连铸机的工艺参数,铸坯厚度为230 mm,许用应变值取为1.5%[14],将上述基本参数代入式(8)可得连铸机基本圆弧半径值:

取最小整数圆弧半径为8000 mm。由于连铸坯所处温度越高,蠕变速率越快,为更好地利用蠕变规律,需要连铸机连续弯曲矫直曲线在温度高的位置曲率变化率大,温度低的位置曲率变化率小。综合考虑原机型的高度和拉坯速度的影响,分别以弯曲段弧长8000 mm和矫直段弧长10 000 mm进行曲线计算。弯曲和矫直曲线计算时初始坐标系不同,如图1所示。

图1 弯曲矫直曲线初始坐标系Fig.1 Original coordinate system of curves
通过坐标系平移和旋转,在同一坐标系下,弯曲段在连接点处的切线斜率为1.3526,而矫直段在连接点处的切线斜率为1.0210,可以看出弯曲段曲线与矫直段曲线在连接点M处无法光滑连接,引入一小段圆弧作为基本圆弧段,考虑铸机高度会影响连铸坯的鼓肚变形,因此最终该圆弧的起始圆心角为-0.7393 rad,终止圆心角为-0.9794 rad,通过该段基本圆弧可将矫直曲线和弯曲曲线光滑无突变地连接起来。
基于原R9300五点弯曲五点矫直直弧型连铸机设计的曲率正弦变化机型曲线参数如表2所示。机型曲线辊列图如图2所示。新曲线弯曲段CD弧长8000 mm,基本圆弧段BC弧长1920.8 mm,矫直段AB弧长10 000 mm。

表2 曲率正弦曲线基本参数

图2 曲率正弦变化机型曲线辊列图Fig.2 Roller curve of new casting machine
图3清晰地表示出五点弯曲五点矫直的机型曲线与曲率满足正弦规律的机型曲线的曲率变化情况。由图3可以看出,多点矫直技术在矫直点处曲率存在突变,而新曲率正弦变化机型曲线的曲率变化连续,并且新曲线基本圆弧段显著缩短,矫直段和弯曲段弧长大大延长,有利于增加蠕变变形和减小应变速率。根据式(2),新曲线矫直段内弧侧表面的应变速率可以由下式计算:
(9)

图3 两种机型曲线曲率对比图Fig.3 Curvature of two casting machines
内弧表面应变速率的理论最大值为5.65×10-5s-1,位于矫直开始点,而在整个矫直过程中,应变速率满足余弦规律,由最大值单调递减为0。
3.2 数值模拟计算
根据某钢铁厂R9300连铸机铸坯断面尺寸1000 mm×230 mm和两种不同的机型辊列建立有限元模型。图4所示为曲率正弦变化机型辊列的有限元计算模型。

图4 曲率正弦变化机型曲线有限元计算模型Fig.4 Finite element model of new casting machine
为了精确对比两种矫直技术的效果,两种曲线模型均采用相同设定,铸坯尺寸相同,采用相同辊径和间隙并均匀布置,忽略了温度场、重力、钢水静压力等参数对其应变造成的影响,通过各个连铸辊转动摩擦力带动铸坯沿曲线位置以工厂实际拉速1.5 m/min匀速运动[15]。由于连铸坯在矫直区域表面温度都在1000℃左右,因此材料属性采取Q460E钢种在Gleeble-3800试验机上的1000 ℃的各项热物性参数,如表3所示。
由于连铸坯在矫直区内弧侧表面受拉,外弧侧表面受压,因此提取矫直区内弧侧表面应变速率的计算值,如图5所示。

表3 Q460E在1000 ℃时热物性参数表

图5 两种机型曲线矫直应变速率对比Fig.5 Strain rate of two casting machines
传统五点弯曲五点矫直机型曲线由于矫直段弧长比较短,矫直变形时间短,并且多点矫直存在应变速率突变,在最后一个矫直点的应变速率达到1.2×10-3s-1,而新的曲率正弦变化机型曲线由于矫直区很长,应变速率变化比较平缓,最大值都在10-5以下,可以看出,新的曲率变化符合正弦规律的机型曲线应变速率明显小于原机型曲线应变速率。
新曲线由于圆弧段的大量减少,变形的时间比原曲线长很多,在矫直段,新曲线变形时间为350 s,原曲线变形时间为60 s。新曲线在矫直段有更长的应变时间,在这段时间连铸坯会发生大量的蠕变变形,从而可以充分利用蠕变变形使铸坯矫直。
4 蠕变试验
对某钢厂生产的Q460E连铸坯取样,其化学成分如表4所示,本次试验采用Gleeble-3800热/力模拟试验机对连铸坯Q460E的高温力学性能和蠕变力学性能进行测试[16]。试件选取直径10 mm、长度为120 mm两端加工有螺纹的圆棒。

表4 Q460E的化学成分(质量分数)
为了更精确地模拟材料在连铸过程中的力学性能,在模拟试验机上采取了与工厂相同的热循环制度。以10 ℃/s的速度加热至1320 ℃,并且保温2 min,然后以3 ℃/s的速度冷却至1000 ℃,通过0.01 s-1恒定应变速率将试件拉断得到应力应变曲线,从而确定Q460E钢在1000 ℃的屈服强度为29.2 MPa。

图6 蠕变试验拉断的试件Fig.6 Specimens after creep tensile tests
采用上述相同的热循环制度,在温度为1000 ℃的条件下,进行恒定应力拉伸试验,应力分别取为18 MPa、19 MP、20 MPa、22 MPa,图6所示为试件蠕变拉断后的形状。
蠕变数据的整理和处理方法参考日本学者平修二的方法,对蠕变曲线进行整理推导。金属材料的蠕变曲线对于各种金属都具有相同的形式,表示某一温度和应力下蠕变的经验公式为
ε=ε0+btn+Kt
(10)
式中,ε0为瞬时应变;b和K分别为应力和温度相关系数;n为硬化指数。
式(10)中第二项表示过渡蠕变的应变分量,第三项表示稳态蠕变的应变分量。忽略瞬时应变,对原始蠕变曲线进行自定义函数拟合,拟合函数为
ε=btn+Kt
(11)
两端取对数得
ln(ε-Kt)=lnb+nlnt
(12)
线性拟合后蠕变本构方程为
εc=exp(0.124 26T-168.3733)σ10t0.36+exp(0.044 36T-88.749 92)σ10t
(13)
式中,εc为蠕变应变;σ为应力,MPa;T为温度,℃。
式(13)揭示了应力与温度对Q460E蠕变的影响规律。把蠕变试验下1000 ℃对应的应力18 MPa、19 MP、20 MPa、22 MPa分别带入蠕变方程,得到理论值,再与试验值做比较,如图7所示。蠕变方程与试验值较吻合,由于整体连铸生产过程的时间相对试验时间比较短,多为2000 s左右,蠕变变形基本发生在过渡蠕变和稳定蠕变阶段,所以蠕变方程式(13)完全可以适用于连铸生产中的蠕变变形研究。

图7 蠕变方程计算值与试验值对比图Fig.7 Comparative data by creep test and creep equation

(14)
由式(14)可知,等号右边第一项随着时间的延长,蠕变应变速率逐渐减小,最终趋近于第二项的最小蠕变应变速率。
当连铸坯温度为1000 ℃时,采用屈服应力29.2MPa代入式(14),得到1000 ℃下最小蠕变应变速率为2.374×10-5s-1,对比曲率正弦变化机型曲线的连铸坯应变速率和五点弯曲五点矫直机型曲线的应变速率可以看出:
曲率正弦变化的机型曲线使连铸坯发生矫直变形的应变速率普遍较小,集中在10-5s-1,接近最小蠕变应变速率;而五点弯曲五点矫直机型曲线在矫直区的应变速率都较大,最大值接近10-3s-1,远大于蠕变应变速率,说明新设计的机型曲线使连铸坯在矫直变形中更多地依靠低于屈服强度作用的蠕变变形,而五点弯曲五点矫直机型曲线则更多依靠大于屈服强度的塑性变形,这必然导致应变速率的增大,也增加了裂纹出现的可能。
5 结论
(1)新机型曲线显著延长了连铸机弯曲段和矫直段弧长,缩短基本圆弧段弧长,并且具有整体铸机高度较低、矫直段应变速率小、蠕变变形量大的特点,充分发挥了材料的高温蠕变特性,使铸坯发生变形。
(2)新曲线的应变速率远小于五点弯曲五点矫直机型曲线的应变速率。新设计的机型曲线使连铸坯在矫直变形中更多地依靠低于屈服强度作用的蠕变变形,而五点弯曲五点矫直机型曲线则更多地依靠大于屈服强度的塑性变形。
在以后的铸机曲线设计中可以参考利用蠕变进行矫直的新方法,进一步缩短基本圆弧段弧长,甚至取消基本圆弧段,最大限度延长矫直段弧长,降低应变速率,从而达到完全的蠕变矫直,大大降低铸坯的矫直裂纹发生率,提高铸坯质量。
[1]TOMONOH.DevelopmentofSteelContinuousCastinginJapan:HasBessemer’sDreamComeTrue?[J].Ironmaking&Steelmaking,2015,42(4):242-251.
[2] 殷瑞钰.中国连铸的快速发展[J].钢铁,2004, 39(z1):1-7.YINRuiyu.RapidDevelopmentofSteelContinuousCastinginChina[J].IronandSteel,2004,39(z1):1-7.
[3]DUFengming,WANGXudong,LIUYu,etal.InvestigationonThermo-mechanicalBehaviorofMoldCornerforContinuousCastingSlab[J].ISIJInternational,2015,55(10):2150-2157.
[4]BRIMACOMBEJK,SORIMACHIK.CrackFormationintheContinuousCastingofSteel[J].Metallurgical&MaterialsTransactionsB,1977,8(2):489-505.
[5]GRILLA,SCHWERDTFEGERK.Finite-elementAnalysisofBulgingProducedbyCreepinContinuouslyCastSteelSlabs[J].Ironmaking&Steelmaking,1979,6(3):131-135.
[6]OKAMURAK,KAWASHIMAH.Three-dimensionalElasto-plasticandCreepAnalysisofBulginginContinuouslyCastSlabs[J].ISIJInternational,1989, 29(8):666-672.
[7]HUESPEAE,CARDONAA,NIGRON,etal.Visco-plasticConstitutiveModelsofSteelatHighTemperature[J].JournalofMaterialsProcessingTechnology, 2000,102(1/3):143-152.
[8] 李宪奎.具有两个光滑连续矫直区的低矮型连铸机[J].钢铁,1996,31(4):31-35.LIXiankui.Low-headContinuousCastingMachinewithTwoSmoothContinuousStraighteningAreas[J].IronandSteel,1996,31(4):31-35.
[9] 满媛,李宪奎,杨拉道.连铸板坯连续矫直过程充分利用钢高温特性的研究[J].塑性工程学报,2008, 15(6):96-101.MANYuan,LIXiankui,YANGLadao.StudyaboutUsingtheElevatedTemperatureCharacteristicsofSteelduringContinuousStraightening[J].JournalofPlasticityEngineering,2008,15(6):96-101.
[10] 马春武,封伟华,储鸿文. 连铸坯弯曲矫直时的变形行为[J]. 钢铁研究学报,2012,24(3):21-27.MAChunwu,FENGWeihua,CHUHongwen.DeformationBehaviorduringBendingorStraighteningofSlab[J].JournalofIronandSteelResearch,2012,24(3):21-27.
[11] 景奉儒,李宪奎,杨拉道,等. 直弧型板坯连铸机连续弯曲矫直曲线的优化研究[J]. 钢铁,2009,44(4):23-27.JINGFengru,LIXiankui,YANGLadao,etal.OptimizationofContinuousBendingandStraighteningCurveofVerticalArcSlabCaster[J].IronandSteel,2009,44(4):23-27.
[12] 黄文, 张卓然, 张兴中,等.连铸机多点矫直的矫直辊反力的解析计算法[J].特种铸造及有色合金, 2015,35(11):1139-1142.HUANGWen,ZHANGZhuoran,ZHANGXingzhong,etal.AnalyticalSolutionofRollerReactingForcesinMultipointStraighteningofContinuousCaster[J].SpecialCasting&NonferrousAlloys,2015,35(11):1139-1142.
[13] 李宁.连续矫直在薄板坯连铸中的应用及其矫直力计算[J].重型机械,2005(1):26-30.LINing.TheApplicationofContinuousStraighteninginCSPandtheCalculationofStraighteningForce[J].HeavyMachine,2005(1):26-30.
[14] 曹广畴.现代板坯连铸[M].北京:冶金工业出版社,1994:102-103.CAOGuangchou.ModernContinuousCastingforSteelSlab[M].Beijing:MetallurgicalIndustryPress, 1994:102-103.
[15]BZVNEKZM,DIERBERGERJ.SomeProblemsofBridgeContactAnalysisUsingMarc[J].ComputationalandExperimentalMethods,2003,38:63-72.
[16] 董志华,陈登福,龙木军,等.20CrMnTi钢连铸坯柱状晶区的高温力学性能[J].材料研究学报,2013,27(3):274-278.DONGZhihua,CHENDengfu,LONGMujun,etal.HighTemperatureMechanicalPropertiesfortheColumnarZoneofSteel20CrMnTi[J].ChineseJournalofMaterialsResearch,2013,27(3):274-278.
(编辑 王旻玥)
New Straightening Technology of Continuous Casting Slabs Based on High-temperature Creep Properties
ZHANG Xingzhong GUO Long FENG Changxi
National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Yanshan University,Qinhuangdao,Hebei,066004
A new straightening technology where the continuous casting slabs might be straightened by full using of high-temperature creep properties was proposed based on the straightening technologies that widely used currently. The new straightening curves were designed herein where the curvatures were changed as sine law. The arc lengths of straightening segments and bending segments were extended significantly. The strain rate in the new curve was less than creep strain rate so that high-temperature creep behavior might be used fully in the straightening processes by finite element method. The parameters of thermo-physical property were confirmed and the creep constitutive equation was derived through the uniaxial tensile tests of Q460E steels on the Gleeble-3800 machine. Strain rates in the new curve were close to the minimum creep strain rates, thus the slabs might be straightened by creep deformations mainly. Due to the lower strain rates, internal cracks caused by bending and straightening might be effectively avoided, and the quality of the slabs was improved.
continuous casting slab; creep straightening; strain rate; straightening curve
2016-06-16
国家自然科学基金资助项目(51275446);河北省自然科学基金资助项目(E2016203492);河北省研究生创新资助项目(2016SJBS027);河北省引进留学人员项目(C2013005012)
TF777.1;TF341.6
10.3969/j.issn.1004-132X.2017.10.016
张兴中,男,1965年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心教授、博士研究生导师。主要研究方向为机械设计及理论和高效连铸技术。获省科技进步三等奖2项,发表论文50余篇。E-mail:Zhangxzh@ysu.edu.cn。郭 龙,男,1985年生。燕山大学机械工程学院博士研究生。冯常喜,男,1991年生。燕山大学机械工程学院硕士研究生。

