不完全测量系统鲁棒SGQKF的传递对准滤波器设计和稳定性分析

陈红梅，刘建娟，程向红，刘楠嶓

（1. 河南工业大学 电气工程学院 机电设备及测控实验室，郑州 450001；

2. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

不完全测量系统鲁棒SGQKF的传递对准滤波器设计和稳定性分析

陈红梅，刘建娟，程向红，刘楠嶓

（1. 河南工业大学 电气工程学院 机电设备及测控实验室，郑州 450001；

2. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

针对复杂环境下运载体观测信息不完全测量并且存在随机干扰不确定的传递对准问题，研究了不完全测量随机不确定系统的鲁棒稀疏网格求积分（H∞-SGQKF）的高斯逼近滤波算法。基于非线性离散系统的最优贝叶斯滤波框架和间断观测滤波算法以及不确定性扰动噪声下的 H∞范数的鲁棒 SGQKF算法，给出了不完全测量的稀疏网格求积分的高斯逼近滤波算法；通过非线性系统随机稳定性理论，分析并给出了系统估计误差和估计误差方差有界的充分条件，同时给出了系统稳定的不完全测量时的丢包率临界值，证明间断观测条件下的不完全测量H∞-SGQKF算法是稳定的。通过传递对准仿真试验和某型激光捷联式惯性导航系统的跑车试验对该算法进行了验证。结果表明，该方法比未采用鲁棒的不完全测量的稀疏网格求积分滤波的传递对准精度有所提高，说明不完全测量的鲁棒稀疏网格求积分滤波算法是正确的、稳定的，并且具有鲁棒性能。

鲁棒稀疏网格求积分卡尔曼；不完全测量系统；鲁棒收敛性分析；传递对准

运载体导航系统采用以惯性导航系统为主，卫星导航或天文导航为辅的组合导航，主要涉及高动态传递对准技术、黑障区导航信息补偿技术、高动态下信息快速捕获技术、宽带数据链通信等关键技术[1]。稀疏网格求积分卡尔曼滤波可用于非线性线性时变系统，并要求系统误差模型准确，过程噪声和测量噪声均值为零，且方差已知，这对应用于运动载体的传递对准技术来说很难实现[2]。运载体的外挂武器和传感器吊舱一般悬挂在机翼或机腹下，而飞行器在高速机动飞行情况下，受空气气流、载荷变更、发动机噪声等多种因素的影响，机体会发生时变结构变形，复合材料的更多使用和现代战斗机的高机动特性使机身和机翼的弹性特性增强[3]，使得子惯导系统的姿态精度不高，此外存在杆臂时间延迟误差等，很难保证建模完全准确[4]。武器一般在发射前或发射中进行动基座条件下传递对准，需要借助外界辅助信息(也称为外部测量信息)解决SINS误差积累问题。运载体始终处于不断运动中，飞行器受到各种天文观测条件约束，要实现较好几何配置关系的导航星通常比较困难，天文导航定位计算过程对导航选星将引起导航星观测信息丢失[5]；同时，空间环境电磁信号密集，信号干扰严重，卫星快速捕获过程中接收机及其天线可能会受到带电粒子以及外层空间的电、磁、紫外线、宇宙射线等的影响，观测量出现间断性随机丢失或延迟[6]。复杂环境下外部量测信息延迟或丢失等不足的不完全量测信息将严重影响导航精度。

为确保攻击精度，运载体的定位精度通常要求达米级，现有的基于完全量测的组合导航算法难以完成不确定条件下导航估计。文献[7-8]提出一种处理不完全量测的滤波器：当rk=0时，表示系统获得实际观测量，观测噪声为Rk；当rk=1时，表示系统未获得实际观测量，系统用上一时刻的测量值来代替，此时假定方差为σ2I的虚拟观测来代替观测噪声，当方差为σ2I取较大值时，相当于系统只进行时间更新，不进行量测更新，这种方法将会减低滤波器性能。文献[9]基于贝叶斯基本框架，给出一套不完全测量的高斯逼近滤波算法。文献[10]分析了系统的稳定性，给出稳定的充分条件。但是针对组合导航系统随机丢包延时等不完全量测的状态估计研究，特别针对同时存在杆臂挠曲误差和各种外界干扰噪声等不确定条件的状态估计研究有待深入，本文将因杆臂挠曲变形引起的杆臂速度误差作为能量有限的不确定性干扰引入 H∞滤波器，利用不确定性噪声的鲁棒性抑制杆臂速度误差的影响，根据鲁棒滤波思想[11]和不完全测量系统高斯逼近[9]算法给出一套不完全测量的鲁棒稀疏网格滤波(H∞-SGQKF)算法,完成传递对准过程，并进行鲁棒算法和稳定性实验验证。

1 不完全测量系统模型和滤波器设计

考虑如下非线性离散系统状态方程加性噪声模型：

不完全测量系统滤波器接收到的测量值可通过如下模型来描述：

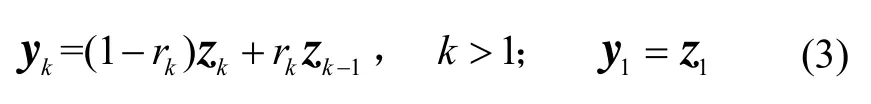
其中：xk∈Rn为n维状态向量；zk∈Rm为系统理想测量输出；yk∈Rm为系统实际测量输出；wk∈Rp和 vk∈Rm为随机过程噪声序列和测量噪声序列，均为0均值白噪声，且有

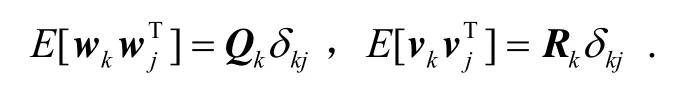
fk(xk)和hk(xk)为已知的非线性系统n维向量函数和m维向量函数；{rk∈R，k>1}，为满足Bernouli分布的序列，其取值为0和1，其不完全测量概率pk为

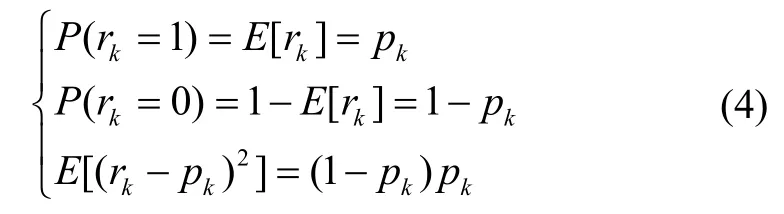
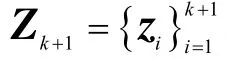
贝叶斯估计不完全测量随机不确定系统 SGQKF的流程如图1所示。

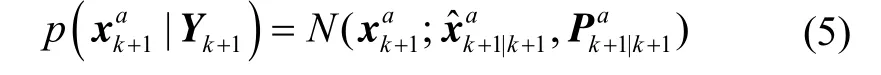
其中，

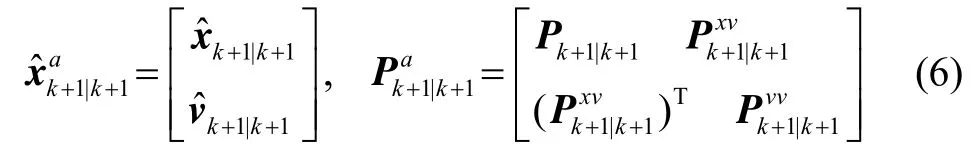
不完全测量随机不确定系统鲁棒SGQKF高斯逼近滤波可通过预测和更新完成，具体表示如下。

滤波器初始化（k=0）设置状态和协方差阵平方根因子的初始值：

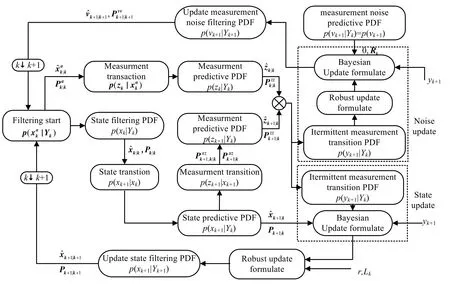
图1 递归贝叶斯估计不完全测量鲁棒SGQKF的流程图Fig.1 Recursive bayesian estimation incomplete measuring robust SGQKF

1）时间更新：k=1, 2, …

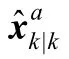
② 通过状态方程和测量方程传播计算预测积分点

这里Np与稀疏网格求积分点集的准则和系统维数有关，Np=2n2+6n+1.

⑤ 测量方程重新传播积分点

2）状态估计更新和测量噪声更新

2 系统误差及相关误差方差阵

2.1 系统估计误差和预测误差

定义系统估计误差和预测误差：

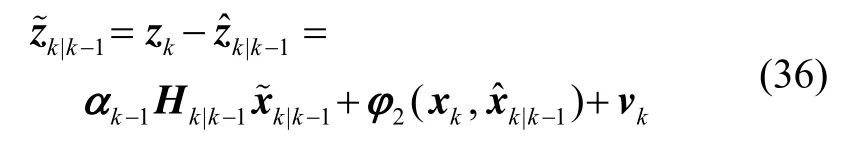
其中，δφ2和εφ2为不为零的正实数，满足

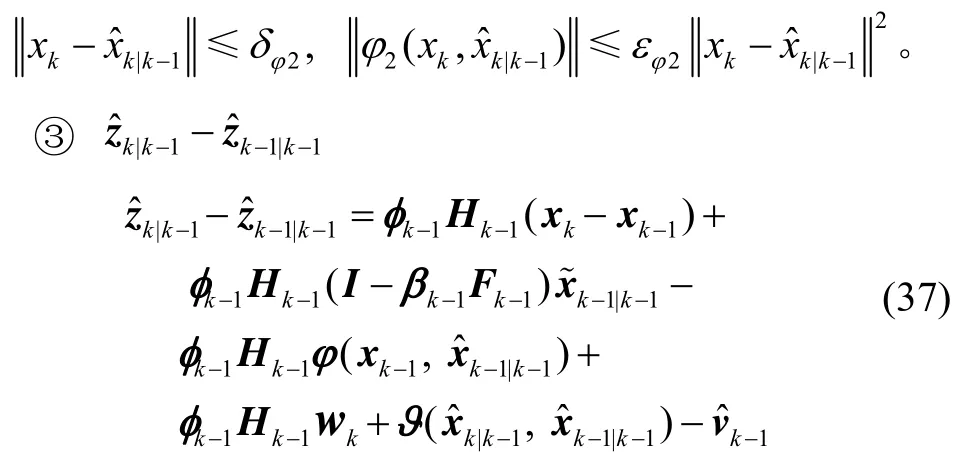
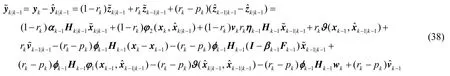
将式(38)代入式(34)：

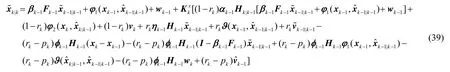
2.2 系统估计误差方差阵和预测误差方差阵

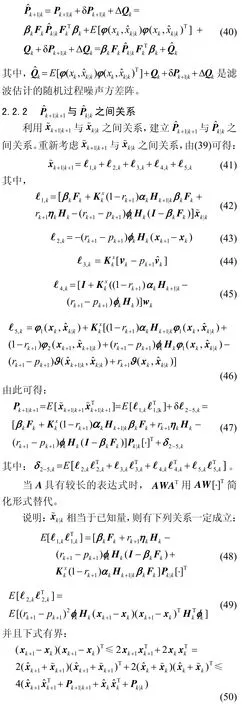
利用矩阵求逆运引理对(26)取逆，可得：

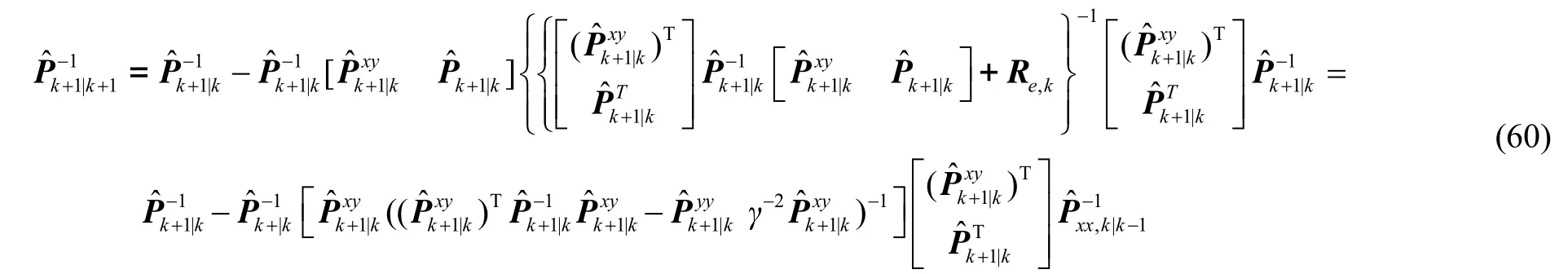
再次利用矩阵求逆引理，将式(60)重新表示为

对比不完全测量的高斯逼近滤波算法，

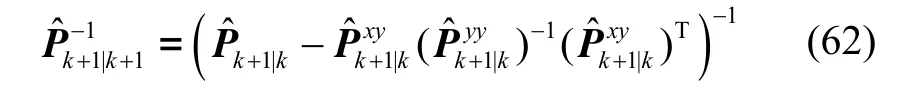
定义：

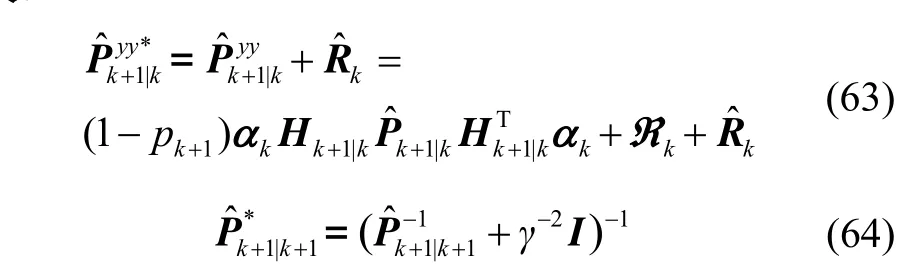
将式(26)(27)(63)代入式(64)整理得到：

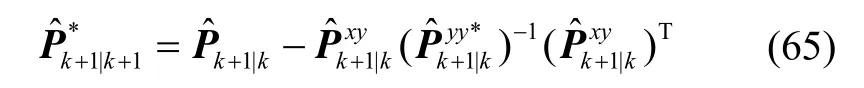
由于

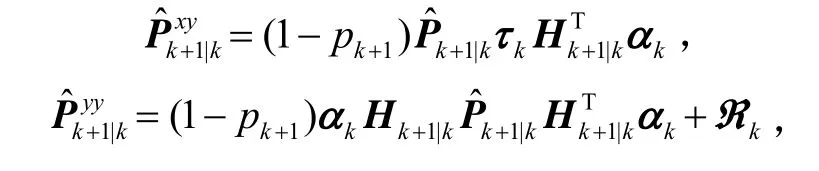
结合式(63)将式(65)重新表示为

其中，

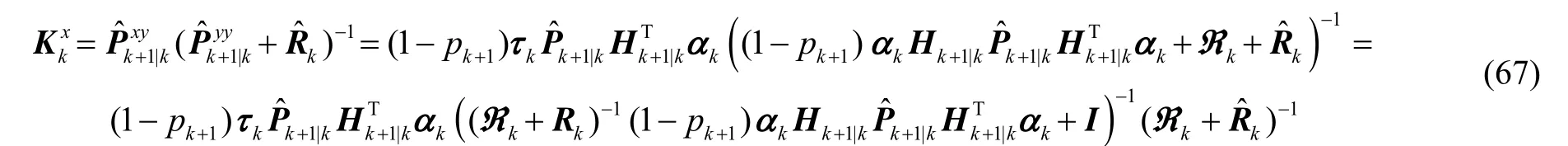
3 系统估计误差随机有界性

以定理1的形式给出不完全测量随机不确定系统鲁棒稀疏网格求积分高斯滤波算法的稳定性充分条件。引入文献[13]的随机过程有界性引理，证明不完全测量H∞-SGQKF滤波算法的稳定性。

定理 1：广义非线性随机系统(1)～(3)以及不完全测量高斯滤波器算法(7)～(30)，若满足如下假设，则(31)中的估计误差x˜k|k为均方内指数有界，则算法稳定。

结合定理1给出的稳定性充分条件，证明满足文献[13]引理的相关结论，则系统估计误差随机有界，证明过程见附录1。

4 系统估计误差方差阵随机有界

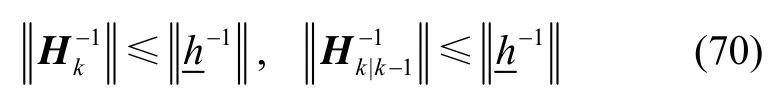
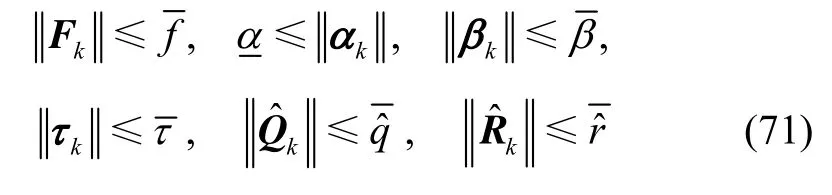
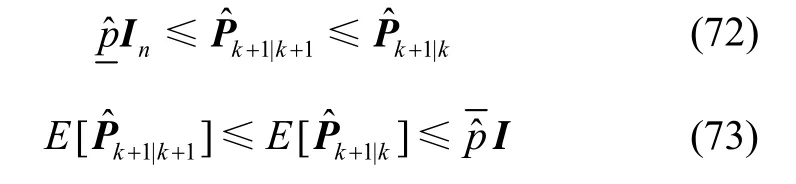
证明过程见附录2。

5 仿真和物理数据验证

为了验证不完全测量随机不确定系统鲁棒SGQKF滤波性能，设计了如下仿真实验和车载跑车试验。

5.1 数学仿真试验

5.1.1 系统参数设置

初始位置为北纬31.98°，东经118.8°，高度50 km,初始速度为5 Ma，加速度计常偏为0.1 mg(1σ)，随机为0.05 mg/Hz1/2陀螺仪的常值漂移为0.1 (°)/h(1σ)，随机噪声为0.01 (°/h)/Hz1/2，基准系统的速度精度为0.5 m/s，姿态更新时间为5 ms，滤波周期为1 s。杆臂和机动轨迹设计采用文献[15]模型，其中静态杆臂为0.15/0.15/ 0.30 m，未建模动态杆臂为8～12 mm，8～14 mm，5～30 mm。仿真时间为300 s，横滚角从0°到34°做摇翼机动，俯仰角和航向角从0°到10°做匀速变化。仿真过程中注入挠曲变形干扰,发射点惯性坐标系(i)作为导航坐标系，采用“速度+姿态”匹配方式进行传递对准，系统的状态方程和观测方程不对主子惯导间的杆臂和挠曲变形进行建模，需要对准的子惯导系统初始失准角的俯仰角、航向角和横滚角方向分别为：50°/20°/30°。不完全测量概率pk为0.885，给定鲁棒因子γ取为3.0，给定矩阵Lk=I。

5.1.2 试验及结果分析

系统存在外观测丢失等不完全测量且同时存在杆臂和挠曲等随机不确定问题时，分别采用未加入鲁棒/增加鲁棒的不完全测量系统，并与系统完全观测鲁棒估计进行了比较，仿真结果如图2所示。黑色点画线表示系统在模型随机不确定时未加入鲁棒的不完全测量；蓝色实线表示系统增加了鲁棒的不完全测量，红色点划线表示系统完全观测。

从图2中可以看出：由于未加入鲁棒方法的不完全测量的滤波器较依赖精确的数学模型和噪声统计方法，当系统中存在不确定因素时，传递对准初期滤波器收敛较缓慢，传递对准后期，特别是在俯仰角姿态发散较大，降低了系统性能；与之对应的增加了鲁棒的不完全测量的滤波器，逼近完全测量的鲁棒滤波器，能够较好地完成传递对准。

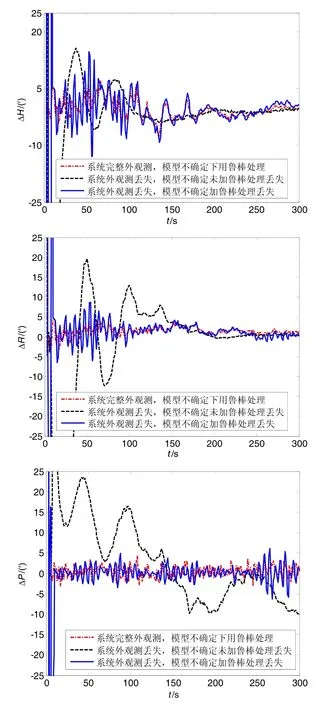
图2 飞行器姿态误差曲线图Fig.2 Attitude error comparisons based on Pehlivanoğlu

5.2 车载跑车试验

为验证不完全测量随机不确定系统鲁棒SGQK算法和稳定性分析在工程应用中的可行性，搭建实验平台如图3所示。

图3 跑车实验平台Fig.3 Experiment platform of trial vehicle

本文采用某型主惯性测量组件（IMU），不对主惯导误差建模，子惯性测量组件由三个 1.0 (°)/h(1σ)精度级别的陀螺和三个 0.5 mg(1σ) 精度级别的加速度计组成。主惯导提供姿态和速度作为外部匹配观测量，GPS输出当地地理系(t)位置/速度信息作为系统导航真值，GPS的水平定位精度为10 m(1σ)，导航坐标系为当地地理坐标。

5.2.1 系统参数设置

传递对准滤波模型的状态方程可由以下 4个矢量方程组成[17]：

滤波器的参数设置如下：

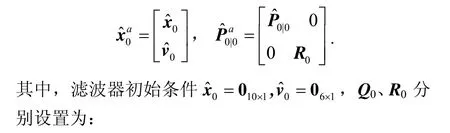
不完全测量的随机丢包率为85%，即不完全测量概率pk为0.85，给定鲁棒因子γ取为1.0，给定矩阵Lk=I。

5.2.2 试验及结果分析

针对实验平台不完全测量问题，采用本文提出的鲁棒方法处理不完全测量系统（蓝色实线5，方案5），分别与文献[7-8]未加入鲁棒方法（绿色点画线 2，方案2）/ 增加鲁棒滤波方法（品红色点画线4，方案4）、文献[9]处理外观测丢失未加鲁棒滤波方法（品红色实线3方案3）和系统完全观测系统（黑色虚线曲线1，方案1）进行了比较，跑车实验结果如图4所示。系统采用GPS位置提供基准，采用主子惯导的完全观测系统作为姿态参考基准。

从图4(a)～(c)可以看出，采用了贝叶斯框架处理的不完全测量（方案3和方案5）优于文献Xia的一步预测方案（方案2和方案4），不完全测量系统增加鲁棒补偿的方案5对姿态的估计精度优于未加鲁棒补偿的方案 3对准精度；从图 4(d)～(e)中经纬度度误差可以看出：方案2误差为262.9/145.5 m，方案3的误差为152.7/61.19 m，方案4的位置误差为48.98/18.77 m，方案5的位置误差为15.58/5.17 m，方案1的位置误差为7.35/3.40 m，方案3处理不完全量测系统性能优于方案2的不完全量测性能；本文的方案5基于鲁棒不完全测量的传递对准位置估计优于方案3方法，比未加入鲁棒的不完全测量系统位置误差更小，逼近系统完全观测的方案 1，性能接近完全观测系统，较好解决了不完全测量系统的性能估计问题。

图4 跑车实验的位置和失准角误差曲线图Fig.4 Position errors and misalignment comparisons based on vehicle experimental platform

6 结 论

针对观测信息不完全测量的随机不确定非线性系统，研究了不完全测量随机不确定系统的鲁棒稀疏网格求积分的高斯逼近滤波算法；通过非线性系统随机稳定性的理论，分析并给出了系统估计误差和估计误差方差有界的充分条件，同时给出了系统稳定的不完全测量丢包率的临界值；不完全测量的鲁棒稀疏网格求积分的高斯逼近算法是稳定的。最后通过数值仿真和跑车实验平台验证了算法和稳定性的可行性。

附录1

证明：由文献[13]引理，首先定义李雅普诺夫函数

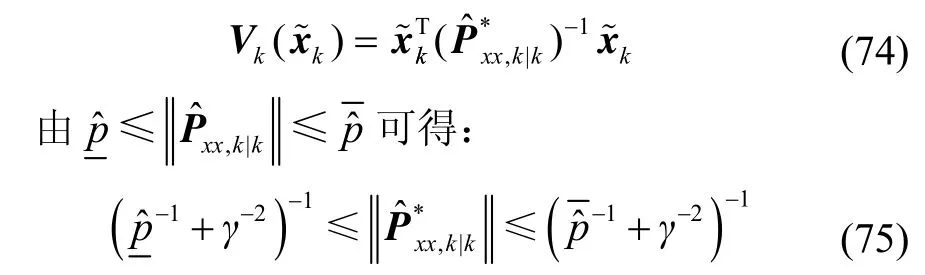
将(75)代入(74)得：

（References）：

[1] 李海林, 吴德伟. 高超声速临近空间武器平台导航方案研究[J]. 飞航导弹, 2012(2): 72-78, 84. Li Hai-lin, Wu De-wei. Research on near-space hypersonic weapon platform navigation methods[J]. Winged Missiles Journal, 2012(2): 72-78, 84.

[2] Bahm C, Baumann E, Martin J, et al. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results[R]. AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies, AIAA 2005-3275: 1-23.

[3] 李四海, 王钰, 刘镇波, 等. 快速传递对准中机翼弹性变形估计方法比较[J]. 中国惯性技术学报, 2014, 22(1): 38-44. Li Si-hai, Wang Yu, Liu Zhen-bo, et al. Comparison of wing distortion estimation methods in transfer alignment [J]. Journal of Chinese Inertial Technology, 2014, 22(1): 38-44.

[4] Spalding K. An efficient rapid transfer alignment filter[C] //AIAA Guidance, Navigation and Control Conference. Montreal, Canada. 1992: 1276-1286.

[5] Peng Hui, Xiong Zhi, Wang Rong, et al. A new dynamic calibration method for IMU deterministic errors of the INS on the hypersonic cruise vehicles[J]. Aerospace Science and Technology, 2014, 32(1): 121-130.

[6] Qin F, Zhan X, Du G. Improvement of global navigation satellite system signal acquisition using different grade inertial measurement units for high dynamic applications [J]. IET Radar, Sonar & Navigation, 2014, 8(3): 233-241.

[7] Li L, Xia Y. Stochastic stability of the unscented Kalman filter with intermittent observations[J]. Automatica, 2012, 48(5): 978-981.

[8] Li L, Xia Y. Unscented Kalman filter over unreliable communication networks with Markovian packet dropouts [J]. IEEE Transactions on Automatic Control, 2013, 58(12): 3224-3230.

[9] Wang X, Liang Y, Pan Q, et al. Gaussian filter for nonlinear systems with one-step randomly delayed measurements[J]. Automatica, 2013, 49(4): 976-986.

[10] Chen Hong-mei, Cheng Xiang-hong, Liu Nan-bo, et al. Stochastic stability of Gaussian filters for nonlinear integrated navigation system with intermittent measurements [C]//IEEE Transportation Electrification Conference and Expo, Asia - Pacific. Busan, Korea, 2016: 145-151.

[11] Chen Hong-mei, Cheng Xiang-hong, Dai Chen-xi, et al. Robust stability analysis of H∞-SGQKF and its application to transfer alignment[C]//Signal Processing Signal Processing. Vol.117, December 2015: 310-321.

[12] Xiong K, hang H Y Z, Chan C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica, 2006, 42(2): 261-270.

[13] Agniel R G, Jury E I. Almost sure boundedness of randomly sampled systems[J]. SIAM Journal on Control, 1971, 9(3): 372-384.

[14] Kluge S, Reif K, Brokate M. Stochastic stability of the extended Kalman filter with intermittent observations[J]. IEEE Transactions on Automatic Control, 2010, 55(2): 514-518.

[15] Pehlivanoğlu A G, Ercan Y. Investigation of flexure effect on transfer alignment performance[J]. Journal of Navigation, 2013, 66(1): 1-15.

[16] 程向红, 王晓飞, 刘峰丽. 稀疏网格求积分滤波算法在SINS/GPS紧组合导航中的应用(英文)[J]. 中国惯性技术学报, 2014, 22(6): 799-804. Cheng Xiang-hong, Wang Xiao-fei, Liu Feng-li. The application of sparse grid quadrature filter on SINS/GPS tightly coupled integration[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 799-804.

[17] 孙进, 徐晓苏, 刘义亭, 等. 基于自适应无迹粒子滤波的SINS大方位失准角初始对准[J]. 中国惯性技术学报, 2016, 24(2): 154-159. Sun Jin, Xu Xiao-su, Liu Yi-ting, et al. Initial alignment of large azimuth misalignment in SINS based on adaptive unscented particle filter[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 154-159.

Design and stability analysis of robust SGQKF transfer alignment filter for incomplete measurement system with stochastic disturbance

CHEN Hong-mei, LIU Jian-juan, CHENG Xiang-hong, LIU Nan-bo
(1. Henan University of Technology, College of Electrical Engineering, Mechanical and Electrical Equipment and Measurement and Control Laboratory, Zhengzhou 450001, China; 2. Key Laboratory of Micro Inertial instrument and Advanced Navigation technology, Ministry of Education, Southeast University, Nanjing 210096, China)

A transfer alignment method based on H∞-SGQKF is developed for the nonlinear systems with intermittent measurements and uncertain stochastic perturbations. A novel Gaussian robust filter with intermittent measurements (H∞-SGQKF) is proposed through presenting Gaussian approximate posterior probability density function (PDF) by embedding the Gaussian approximate filter into the robust mechanism of H∞ suboptimal filter. Using the direct method of Lyapunov, we prove that, under some conditions, the proposed filter is an exponential observer, i.e., the dynamics of the estimation error is exponentially stability, and the error covariance matrices are nominal and robust convergent by providing the existence of a super-threshold value for the intermittent measurement probability. At last, a transfer alignment method based on the proposed filter is presented, and the ground vehicle test of missile-board SINS and a numerical example show that the obtained estimator has good estimation performance.

robustness sparse grid Kalman; nonlinear system with intermittent measurements; robust convergence analysis; transfer alignment

U666.1

A

1005-6734(2017)02-0171-11

10.13695/j.cnki.12-1222/o3.2017.02.007

2017-01-20；

2017-03-26

国家自然科学基金（61374215，61304529）；东南大学微惯性仪表与先进导航技术教育部重点实验室（B 类）开放基金资助项目（SEU-MIAN-201702）；河南省教育厅高等学校重点科研项目（17B590001）；河南工业大学博士基金（2016BS005）；河南省科技厅自然科学项目（172102210214）

陈红梅（1977—），女，博士，从事导航算法研究。E-mail: chenhongmei_seu@163.com