有序不可区分串的属性约简增量更新算法*

梁宝华，严小燕

巢湖学院 信息工程学院，合肥 238000

有序不可区分串的属性约简增量更新算法*

梁宝华+，严小燕

巢湖学院 信息工程学院，合肥 238000

+Corresponding author:E-mail:liangbh426@126.com

LIANG Baohua,YAN Xiaoyan.Incremental updating algorithm for attribute reduction based on ordered indistinguishable string.Journal of Frontiers of Computer Science and Technology,2017,11(5)：842-850.

属性约简;有效元素对;不可区分串;增量更新

1 引言

为处理模糊、不确定数据，1982年波兰数学家Pawlak提出了一个强有力的数学工具——粗糙集理论[1]，它是在无需任何先验知识的前提下处理不精确数据，目前已广泛应用于数据挖掘、人工智能、金融分析等领域。属性约简是粗糙集理论研究的重点内容之一，是指用较少的特征描述事物，且不影响事物的区分能力，剔除不必要的数据。为了有效地对数据进行约简，广大研究者提出了很多属性约简算法[2-8]，但多数是针对静止不变的信息系统。现实生活中的信息是变化不定的，为了处理多变的信息系统，学者们相继提出了少数增量更新算法[9-15]。官礼和在文献[9]中设计了一种利用差别矩阵的启发式增量更新算法，可快速得到最小属性约简集，但算法在更新差别元素时，未能有效剔除无用的元素，消耗大量的时间资源。胡峰在文献[10]中设计了基于正区域的增量更新算法，能够根据不同元素是否属于正区域进行准确定位，根据具体情况作相应处理，有效提高了动态数据的约简效率，但未能充分利用更新的核，对加入对象属于负区域，或引起数据不一致情况未能很好地处理。刘洋博士在文献[11]中虽然给出了基于差别矩阵增量更新算法，但因未将决策表进行化简，导致算法有很高的时间、空间复杂度。增量更新算法，旨在适应变化的数据集。当数据集变化后，无需重新将原来的数据进行约简，而根据相应变化情况对新增加的数据进行约简，既保持约简集的区分能力，又减少约简时间。多数差别矩阵的增量更新算法，均是以差别元素最多的属性为重要属性，即每次需扫描更多的差别元素；在约简过程中，传统算法也未能有效地将已区分的数据过滤，导致消耗大量的系统资源。

为解决差别矩阵类的增量更新算法存在的不足，本文提出每次选择最少的元素，且选择最重要的属性。在约简过程中，不断将基数为1的子划分有效删除，加速寻找最小约简集，有效提高时间效率。本文工作概括如下：（1）借助文献[3]中用到的方法求简化决策表及正、负区域集。（2）根据改进差别矩阵定义，给出有效比较元素对定义，并将每个元素对给予唯一编号。将元素对在条件属性Ci上取值相同的元素对编号顺次连接形成有序表。（3）根据有序表的长短决定属性的重要性。（4）当有新增对象加入时，根据相应条件，动态增删有序表中信息，可快速得到更新后的约简集。（5）利用实例和实验验证算法的正确性和有效性。

2 粗糙集相关概念

决策表S=(U,A,V,f)，其中U为论域，A=C⋃D，C⋂D=∅，C为条件属性，D为决策属性，V是A上的值域；f∶A→V是一个信息函数；∀a∈A,x∈U，有f(x,a)∈Va。

定义1对于B⊆A决定不可分辨关系：

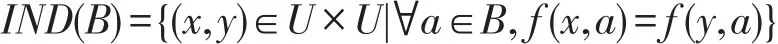
可简化为U/B；U/B的元素为等价类，含x的等价类记为：

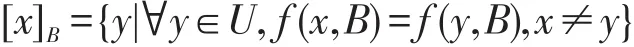
定义2B⊆A，用U B表示B的所有等价类的集合，用[x]B表示在等价关系B下包含元素x(x∈U)的等价类。对于论域给定决策表S=(U,A,V,f)，对于任意子集X⊆U和不可分辨关系IND(B)：

定义3条件属性集C相对于D的正区域定义为，简记为UPOS，负区域为UNEG= U-UPOS。

定义4[12]决策表S的改进差别矩阵M={mij}定义为：

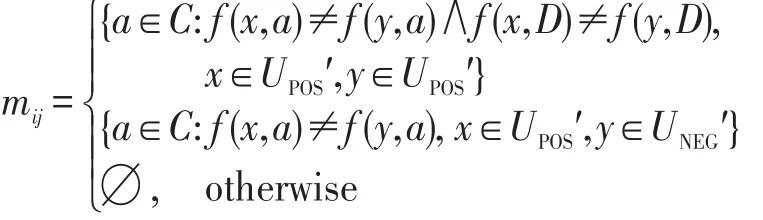
其中，UPOS′简化决策表中正区域部分，UNEG′为负区域部分，简化决策表是U/C每个子划分中取第一个元素组成的决策表。

定义5对于简化决策表S′=(U′,A,V,f)，U′为简化后的论域，U′=UPOS′⋃UNEG′,UPOS′、UNEG′分别为简化决策表中的正区域和负区域集，可将相互比较的元素形成元素对Mpair，定义如下：

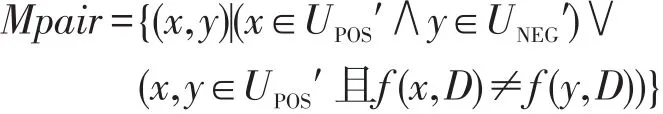
定理1定义4的改进差别矩阵元素与定义5 Mpair的元素对具有等价性。

证明（1）由改进差别矩阵M及Mpair定义可得，M中的a所对应的样本x、y组成的元素对一定能在Mpair中找到。

（2）Mpair中的元素也一定能找到M中所对应的(x,y):（以下的a为条件属性C中的任意一个）。∀(x,y)∈Mpair，当x∈UPOS′∧y∈UNEG′时，假设找不到任何 f(x,a)≠f(y,a)，因为 a具有任意性，所以有f(x,C)=f(y,C)，又Mpair中的(x,y)来源于简化决策，而简化决策表中无重复元素，即不存在 f(x,C)= f(y,C)，因此假设不成立，也即在M中能找到一个a及相对应的(x,y)，使 f(x,a)≠f(y,a)；同理可得，当x∈UPOS′∧y∈UPOS′∧f(x,D)≠f(y,D)时，也能在M中找到一个a使 f(x,a)≠f(y,a)。

综合（1）、（2）得M与Mpair元素具有等价性。□

定义6设每个元素对给定一个唯一编号，关于属性集B的所有不可区分元素对对应的编号形成的有序序列称不可区分序号串：

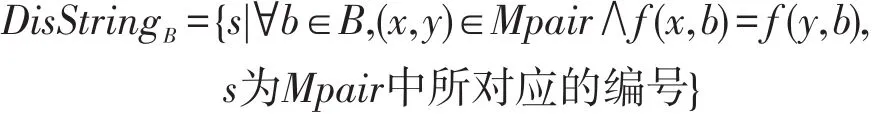
定理2对于简化决策表S′=(U′,C⋃D,V,f)，C为条件属性，设B⊆C,b⊆C-B，则有DisStringB⋃b⊆DisStringB。

证明设∀s∈DisStringB⋃b，编号s所对应的两个比较样本分别为x和y,根据定义6可知，(x,y)∈Mpair且 f(x,B⋃b)=f(y,B⋃b)，因为B⊆B⋃b，所以一定有f(x,B)=f(y,B)。又因为 s具有任意性，所以有 s∈DisStringB，因此DisStringB⋃b⊆DisStringB。 □

性质1不可区分序号串DisStringB长度越短，区分能力越强。

证明根据定义5，可得对于一个给定的决策表，Mpair的元素是一定的。现DisStringB记录了条件属性B关于Mpair中不可区分的元素对，若DisStringB组成的字符串长度越短，表明越少的样本在条件属性B上不可区分。相反，可区分的样本越多，也即可区分能力越强。 □

3 有序不可区分串的属性约简增量更新算法

3.1 有序不可区分串的属性约简算法

传统的差别矩阵算法，需消耗大量内存空间存储差别信息矩阵。在约简过程中，每次挑选区分度最高的属性加入简约集，但区分度最高，意味着可区分串的长度最长，也即每次扫描的元素对越多，造成时间的浪费。鉴于此，为加速寻找最小约简集，本文以一种有序不可区分串为依据，每个条件属性都对应一个不可区分串，可独立存放于内存，这样无需将所有条件属性的不可区分串同时存储于内存，大大减少内存消耗。此外，每次选择最短的不可区分串，有效减少了扫描对象，降低了时间、空间消耗。

算法1不可区分串的属性约简算法

算法中，在求MinString⋂DisStringCi时，因为这两个串均是有序的，所以时间复杂度为O(m+n),m、n分别为MinString与DisStringCi的元素个数。步骤1时间复杂度为O(|C||U|)；步骤2时间复杂度为O(|UPOS′||U′|)；步骤3时间复杂度可忽略不计；步骤4时间复杂度为O(|C||UPOS′||U′/C|)；步骤5在最好情况下时间复杂度为O(|C|min(|DisStringCi|))+O(|C|min(|DisStringCj|))，因为|DisStringCi|也即是不可区分串的长度，最坏情况下是O(|UPOS′||U′|)，所以步骤5的时间复杂度为O(|C|min(|DisStringCi|+|DisStringCj|))。总时间复杂度为max(O(|C||UPOS′||U′/C|),O(|C|min(|DisStringCi|+|DisStringCj|)),其中min(|DisStringCi|+|DisStringCj|)为两个较短的不可区分串。空间资源消耗主要是用来存储条件属性的不可区分串，由于在实验时，可将每个条件属性的DisStringCi依次取出，无需将所有的DisStringCi同时驻留内存，因为DisStringCi的长度不可能超过|UPOS′||U′|，所以空间复杂度为O(|UPOS′||U′|+max(|DisStringCi|))。

3.2 增量更新算法

3.2.1 增量情况分析

现实生活中，信息系统的数据是不断变化的。当增加数据对象时，如何充分利用前期约简结果得到新的约简集，这一问题引起了多数研究者的关注。经研究分析，新增对象与改进差别矩阵相比，存在以下几种情况（设x为原数据集对象，y为新增对象）：

（1）∃x∈UPOS′，对∀Ci∈C有 f(x,Ci)=f(y,Ci)：若 f(x,D)=f(y,D)，则Mpair保持不变；

若 f(x,D)≠f(y,D)，将x变为UNEG′，则Mpair中删除所有UNEG′与x组成的元素对，原来UPOS′与x构成的Mpair元素对对应的序号加标记“*”。

证明∃x∈UPOS′，对∀Ci∈C有 f(x,Ci)=f(y,Ci)，说明数据源中有样本与y样本在条件属性C上取值重复，设此样本为x，若 f(x,D)=f(y,D)，则完全重复，故加入y不影响约简结果，Mpair也不变；若 f(x,D)≠f(y,D)，说明条件属性值相同，但决策值不同，根据负区域定义可得，因y的加入，使x变为负区域，x与y任选其一加入负区域集，设取x加入。再根据Mpair定义得，负区域集各元素间无需比较，因x已变为UNEG′，所以删除Mpair中原来与x组成的且带“*”标记的元素对，并将Mpair中原来与x构成的未加标记“*”元素对加标记“*”，以便识别新组建的关系。 □

（2）∃x∈UNEG′，对∀Ci∈C有 f(x,Ci)=f(y,Ci)，则Mpair不变。

证明根据负区域定义得y∈UNEG′。根据Mpair定义得y无需与负区域集的其他元素进行比较，而y与正区域元素比较的情况与x完全相同，由于x与正区域元素比较的元素对情况已包含在Mpair中，故Mpair不变。 □

（3）∀x∈U′,f(x,C)≠f(y,C),则将 y加入到UPOS′中，改变Mpair的值：

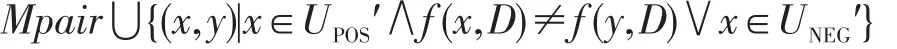
证明因为∀x∈U′∧f(x,C)≠f(y,C),所以y在U′中无数据与之相对应，当y加入U′时，由UPOS′定义可得y∈UPOS′。根据Mpair定义得，y与UPOS′中元素构成元素对{(x,y)|x∈UPOS′∧f(x,D)≠f(y,D)}，y与UNEG′中元素构成元素对{(x,y)|x∈UNEG′}，合并得Mpair⋃{(x,y)|x∈UPOS′∧f(x,D)≠f(y,D)∨x∈UNEG′}。 □

3.2.2 增量更新算法描述

算法2增量更新算法

算法复杂度分析：设新增对象y，在计算步骤1过程中，当 f(x,D)=f(y,D)时，计算用时O(|C||UPOS′|)，当f(x,D)≠f(y,D)时，计算用时O(|C||UPOS′|)+O(|Mpair|)+ min(O(|Reduce|2|DisString(Ci)|)，O(|Mpair|)为定义5元素对的个数，即O(|C||UPOS′||U′|)；步骤2用时为O(|C||UNEG′|)；计算步骤3过程中，因新增对象y，所以更新DisStringCi用时O(|C||UPOS′||U′|)，求最短不可区分串用时O(|C||UPOS′| |U′|)+min(O(|Reduce|2|DisStringCi|))。因为O(|DisStringCi|)≺O(|UPOS′||U′|)，所以算法总的时间复杂度为max(O(|C| |UPOS′||U′|),O(|Reduce|2|UPOS′||U′|))。算法的空间消耗主要用来存储每个条件属性的不可区分串，因为在访问数据时，可将条件属性的不可区分串逐一存取，所以空间复杂度为O(|UPOS′||U′|)。

文献[13]算法的时间、空间复杂度均为O(|C|2||U′|2)，文献[14]算法的时间复杂度为max(O(|C||U′|),O(|Reduce|2|UPOS′||U′|))，空间复杂度为O(|C||UPOS′||U′|)。虽然文献[14]的时间复杂度略低于算法2，实际知识发现过程中，算法2每次取的是最短的不可区分串，因此时间消耗上与文献[14]相差不大，但其空间复杂度大大超过算法2。算法2综合来看，计算的时间、空间效果要优于文献[13-14]。

4 示例及实验分析

下面以决策表S=(U,C,D,V,f)为例进行分析，决策表如表1所示。

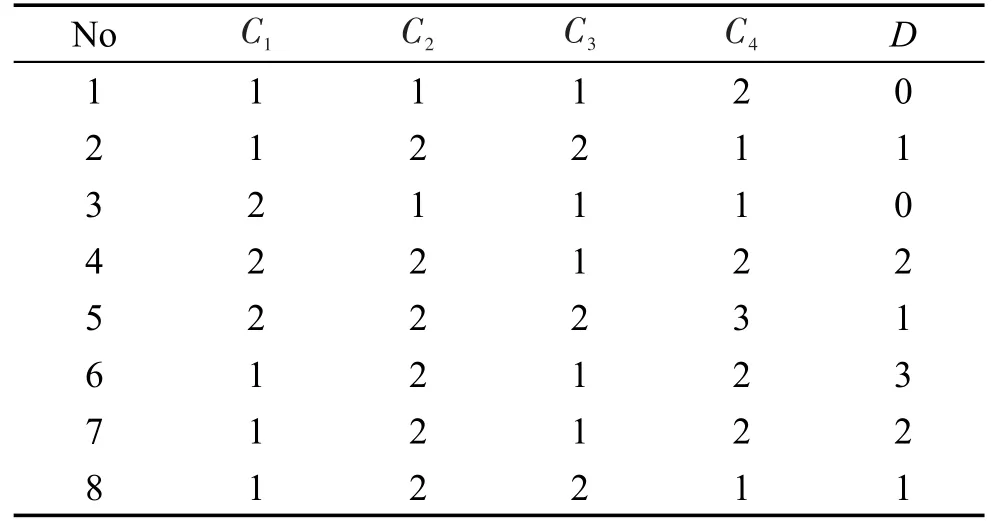
Table 1 Decision table表1 决策表

4.1 属性约简过程示例

简化决策表S得S′，并根据文献[3]计算S′的正区域集数据对象序号依次为{1,2,3,4,5}、负区域对象有{6}。根据定义4可得到Mpair，并统一编号如表2所示。

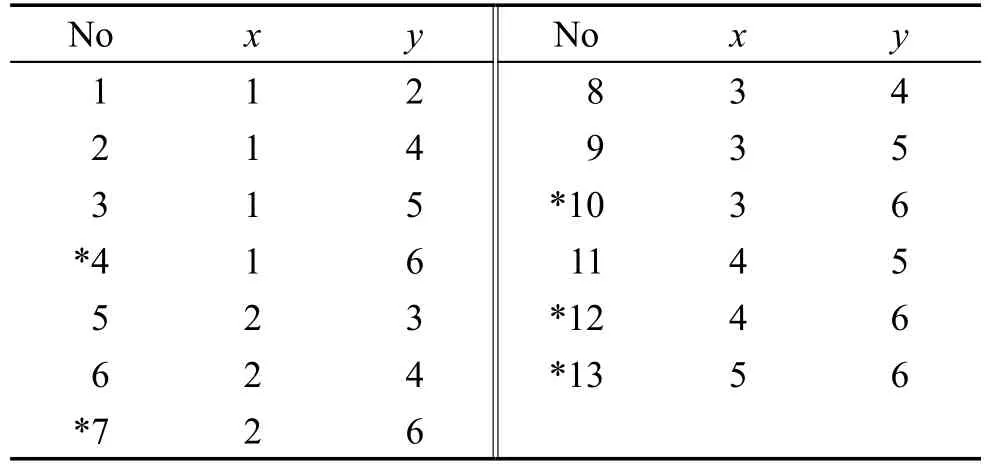
Table 2 Element pairs of Mpair表2 Mpair元素对

将U′按条件属性划分得：

其中，每个子划分中带下划线部分的元素决策值相等，根据定义5得，具有相同决策值的样本无需比较。将每个子划分中的样本两两组成元素对，并根据Mpair中的元素得到元素对的编号，收集成一个有序的不可区分串得：

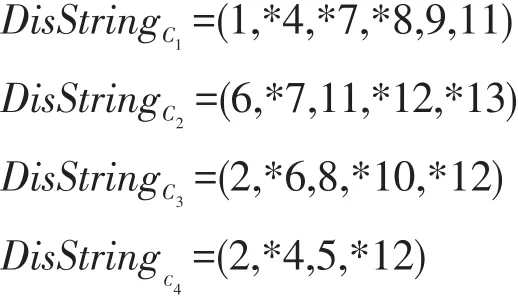
DisStringC4长度最短，因此取Reduce={C4},Min-String=(2,*4,5,*12)。同理，；选择C1加入约简集得Reduce={C1,C4}(C1与C2任选一个)， MinString={*4},，故算法终止，将C2并入Reduce得Reduce={C1,C2,C4}。

4.2 增量更新过程示例

（1）当新增对象为y={1,2,2,1,1}时，对于Ci∈C，存在x2∈UPOS′，使得 f(y,Ci)=f(x2,Ci)，根据算法步骤1可知，Reduce={C1,C2,C4}不变；当新增对象为y={1,1,1,2,1}时，对于Ci∈C，存在 x1∈UPOS′，使得f(y,Ci)=f(x1,Ci)∧f(x1,D)≠f(y,D)。根据算法步骤1可知，编号为1、2、3的元素对分别加上标记“*”，删除*4号元素对，UPOS′={2,3,4,5}，UNEG′={1,6}，反向删除{C2}得DisStringReduce=∅，故Reduce={C1,C4}。

（2）当新增对象为y={1,2,1,2,4}时，对于Ci∈C，存在x6∈UNEG′，使得 f(y,Ci)=f(x6,Ci)。根据算法步骤2可知，属性约简Reduce={C1,C4}不变。

（3）当新增对象为y={1,1,2,1,0}时，对∀x∈UPOS′,∃Ci∈C，使得 f(y,Ci)≠f(x,Ci)。根据算法步骤3可知，更新Mpair。

Mpair元素对更新结果如表3所示。

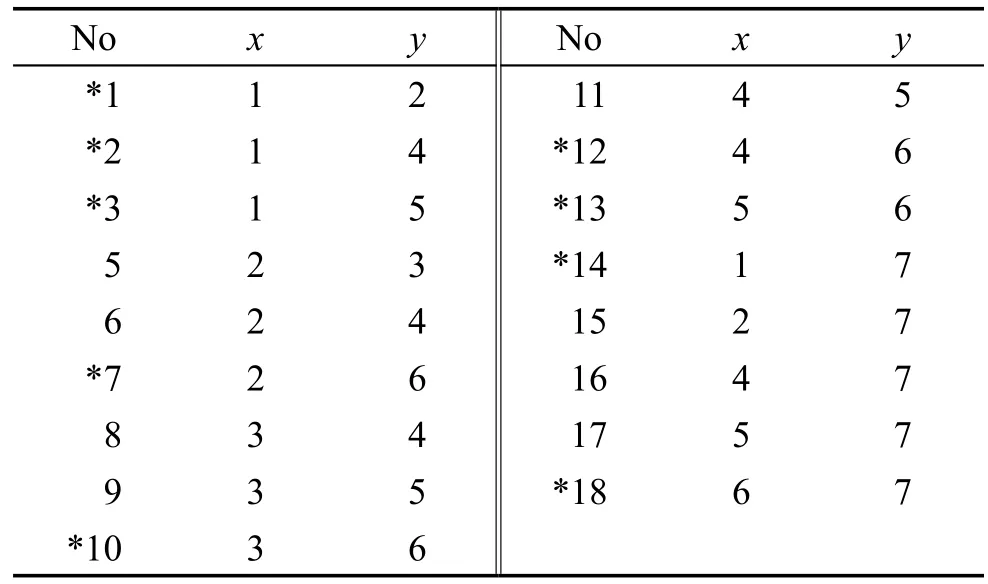
Table 3 Updating element pairs of Mpair表3 Mpair元素对更新

因增加新对象y，使各条件属性增加了新的不可区分元素对，根据算法步骤3可知DisStringC1增加部分为(*14,15,*18)，增加部分为(*14),增加部分为(15,17)，增加部分为(15)。因DisStringReduce=(15)非空，所以更新Reduce。因，所以将属性C2并入Reduce，更新Reduce={C1,C2,C4}，算法终止。

4.3 实验比较

为进一步验证本文增量更新算法2与其他同类算法的性能，在WindowsXP下,开发工具为VC6.0，CPU 2.3 GHz，内存2 GB环境下编程。本文选用UCI机器学习数据库中的5个数据集测试，具体数据集情况如表4所示。D1～D5依次表示UCI中的数据集Patient、Cancer、Forest、Car、Mushroom，|U|为数据集对象数，|U′|为简化后数据集对象数，|C|为条件属性个数，|UPOS′|为正区域对象数，|Base|为基准数。下面分别以雷晓蔚的文献[13]与钱文彬的文献[14]及本文算法2，从空间及时间上进行比较。

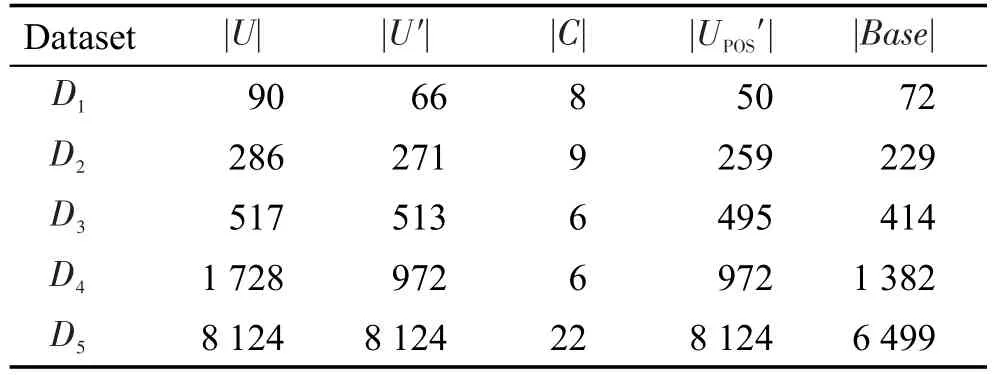
Table 4 Test dataset表4 测试数据集

（1）以UCI数据库中的5个数据集进行空间的测试，共进行了5次计算，取平均值。表5表示各算法存储信息矩阵的元素个数。

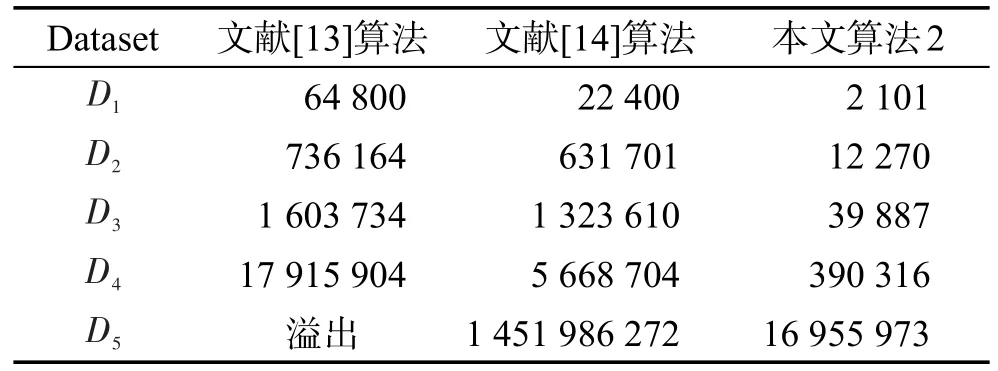
Table 5 Space comparison of 3 algorithms表5 3种算法的空间比较

从空间资源消耗上说，文献[13]算法的空间复杂度为O(|C||U|2)，文献[14]算法的空间复杂度为O(|C||U′||UPOS′|)。当|U|≈|U′|时，文献[13]与文献[14]算法的复杂度较接近，但文献[13]算法未能避免决策值相同元素间的比较，导致空间效率较文献[14]低。本文算法2的空间消耗不到文献[14]算法的1/|C|，实现时只需存储最短的不可区分串。若测试数据集中有大量重复数据，效果更加明显，如数据集D1、D4在挖掘时，算法2中有效剔除了无需区分对象，使所需空间远比文献[13]的1/|C|小。文献[13]算法在计算数据集Mushroom约简时，由于数据量大，属性多，无法将信息矩阵存入到内存，产生溢出。而本文算法2只需少量空间就可得到约简结果，节省大量空间资源。

（2）对UCI数据库中的5个数据集进行时间消耗的测试，Ti为算法需要的时间，以秒为单位，Ri为约简后的属性个数，共进行了5次计算，取平均值，并且取每个原数据集80%的数据作为基准数，其余作为增量部分，结果如表6所示。

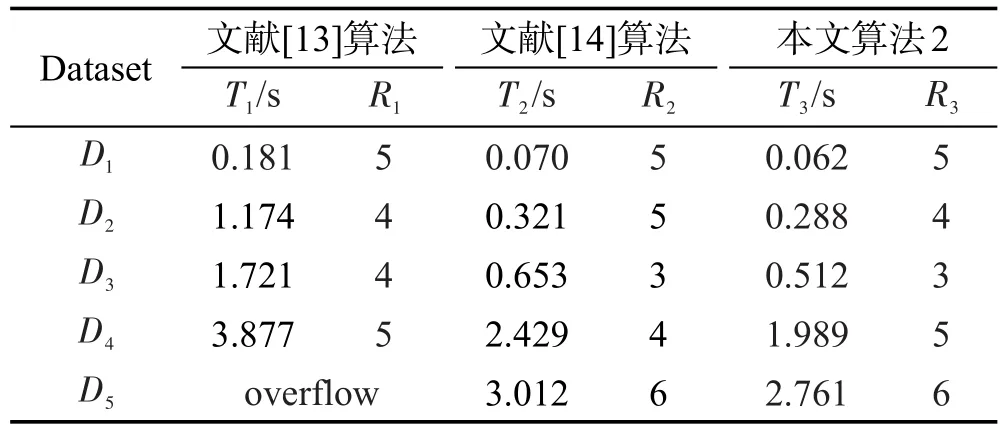
Table 6 Comparison of 3 incremental updating algorithms表6 3种增量更新算法的比较

文献[13]、文献[14]及本文算法均利用正、负区域模型，计算动态更新情况下的约简集，由表6数据可知，约简结果基本一致。在数据集的维数及数据量较小的情况下，时间效果不明显，如D1只有90个样例，文献[13]约简时间0.181 s，而文献[14]约简时间0.070 s，本文算法2约简时间0.062 s。但随着数据规模的增大，本文算法2在约简时，由于每次取不可区分串最短的串为选择重要属性的依据，加速了剪枝效果，时间效果更为明显。如D5有数据8 124条，文献[13]因不能有效剪枝，所以无法完成约简过程，产生数据溢出现象，而本文算法2只需2.761 s，比文献[14]的时间3.012 s稍优越。文献[10]的时间复杂度为O(|C2||U|2)，文献[14]与算法2的时间复杂度为max(O(|C||UPOS′||U′|),O(|Red|2|UPOS′||U′|))，与|U′|、|UPOS′|关系较大，因此|U′|、|UPOS′|的大小严重影响文献[14]与算法2的运算时间，但对文献[13]算法时间影响不大。上述数据集中，D4出现大量重复。表面上看，D4虽然比D3的数据量大很多，但运算时间上，文献[13]明显没有文献[14]和算法2的效果好，因此文献[14]与本文算法2更适应于重复样本多的数据集约简。

5 结束语

关于属性约简算法，多数只针对静态数据集的情况。现实生活中，数据是不断变化的，当有新数据加入时，可能会引起约简集的变化。为了充分利用前期的约简结果，减少大量重复性的计算，本文提出比较元素对概念Mpair，并以每个条件属性的不可区分元素对的数量多少为重要依据，设计一种动态增量更新算法，根据加入对象的不同情况，进行相应处理，动态更新约简集。由于每次以最短的不可区分串为选择的条件，加速了寻找约简集的速度，而同类算法均以最长的可区分元素对为依据，不能有效剪枝。为更进一步加快约简速度，且适应现代计算机体系结构的变化，下一步工作是：研究如何将数据集分成n块，适应多处理器的计算机运行，让每个处理器同时处理，达到并行处理效果。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11(5):341-356.

[2]Wang Jue,Wang Ju.Reduction algorithm based on discernibility matrix:the ordered attributes method[J].Journal of Computer Science and Technology,2001,16(6):489-504.

[3]Liang Baohua,Wang Shiyi,Cai Min.Heuristic attribute reduction algorithm based on order table[J].Computer Engineering,2012,38(2):51-53.

[4]Miao Duoqian,Hu Guirong.Aheuristic algorithm for reduction of knowledge[J].Computer Research and Development,1999,36(6):681-684.

[5]Qian Yuhua,Liang Jiye,Pedrycz W,et al.Positive approximation:an accelerator for attribute reduction in rough set theory[J].Artificial Intelligence,2012,174(9/10):597-618.

[6]Ge Hao,Li Longshu,Yang Chuanjian.Improvement to quick attribution reduction algorithm[J].Journal of Chinese Computer Systems,2009,30(2):308-312.

[7]Zhang Qinghua,Xiao Yu.New attribute reduction on information entropy[J].Journal of Frontiers of Computer Science and Technology,2013,7(4):359-367.

[8]Chen Tangmin.Research of the heuristic reduced algorithm based on the separating capacity[J].Chinese Journal of Computers,2006,29(3):480-487.

[9]Guan Lihe,Wang Guoying.An incremental updating algorithm for attribute reduction set of decision tables[J].Journal of Frontiers of Computer Science and Technology,2010, 4(5):436-444.

[10]Hu Feng,Wang Guoyin,Huang Hai,et al.Incremental attribute reduction based on elementary sets[C]//LNCS 3641: Proceedings of the 10th International Conference on Rough Sets,Fuzzy Sets,Data Mining,and Granular Computing, Regina,Canada,Aug 31-Sep 3,2005.Berlin,Heidelberg: Springer,2005:185-193.

[11]Liu Yang,Feng Boqin,Zhou Jiangwei.Complete algorithm of increment for attribute reduction based on discernibility matrix[J].Journal of Xi’an Jiaotong University,2007,41 (2):158-161.

[12]Yang Ming.An incremental updating algorithm of the computation of a core based on the improved discernibility matrix[J].Chinese Journal of Computers,2006,29(3):407-413.

[13]Lei Xiaowei.The matrix approaches of rough sets[J].Computer Engineering andApplications,2006,42(17):73-75.

[14]Qiang Wenbin,Yang Bingru,Xu Zhangyan,et al.Efficient algorithm for dynamic attribute reduction based on a matrix [J].Journal of University of Science and Technology Beijing,2013,35(2):249-255.

[15]Hu Feng,Dai Jin,Wang Guoyin.Incremental algorithms for attribute reduction in decision table[J].Control and Decision,2007,22(3):268-272.

附中文参考文献：

[3]梁宝华,汪世义,蔡敏.基于顺序表的启发式属性约简算法[J].计算机工程,2012,38(2):51-53.

[4]苗夺谦,胡桂荣.知识约简的一种启发式算法[J].计算机研究与发展,1999,36(6):681-684.

[6]葛浩,李龙澍,杨传健.改进的快速属性约简算法[J].小型微型计算机系统,2009,30(2):308-312.

[7]张清华,肖雨.新的信息熵属性约简[J].计算机科学与探索,2013,7(4):359-367.

[8]陈堂敏.基于区分能力大小的启发式约简算法的研究[J].计算机学报,2006,29(3):480-487.

[9]官礼和,王国胤.决策表属性约简集的增量式更新算法[J].计算机科学与探索,2010,4(5):436-444.

[11]刘洋,冯博琴,周江卫.基于差别矩阵的增量式属性约简完备算法[J].西安交通大学学报,2007,41(2):158-161.

[12]杨明.一种基于改进差别矩阵的核增量式更新算法[J].计算机学报,2006,29(3):407-413.

[13]雷晓蔚.粗集理论的矩阵方法[J].计算机工程与应用, 2006,42(17):73-75.

[14]钱文彬,杨炳儒,徐章艳,等.一种快速的动态属性约简矩阵算法[J].北京科技大学学报,2013,35(2):249-255.

[15]胡峰,代劲,王国胤.一种决策表增量属性约简算法[J].控制与决策,2007,22(3):268-272.

LIANG Baohua was born in 1973.He received the M.S.degree from Guangxi Normal University in 2007.Now he is an associate professor at Chaohu University.His research interests include data mining and rough set,etc.

梁宝华（1973—），男，安徽无为人，2007年于广西师范大学获得硕士学位，现为巢湖学院副教授，主要研究领域为数据挖掘，粗糙集等。

YAN Xiaoyan was born in 1984.She is a lecturer at Chaohu University.Her research interests include computer network and artificial intelligence,etc.

严小燕（1984—），女，安徽庐江人，硕士，巢湖学院讲师，主要研究领域计算机网络，人工智能等。

欢迎订阅2017年《计算机科学与探索》、《计算机工程与应用》

《计算机科学与探索》为月刊,大16开,单价48元,全年12期总订价576元,邮发代号：82-560。邮局汇款地址：

北京619信箱26分箱《计算机科学与探索》编辑部(收) 邮编：100083

《计算机工程与应用》为半月刊,大16开,每月1日、15日出版,单价45元,全年24期总订价1080元,邮发代号：82-605。

邮局汇款地址：

北京619信箱26分箱《计算机工程与应用》编辑部(收) 邮编：100083

欢迎到各地邮局或编辑部订阅。个人从编辑部直接订阅可享受8折优惠！

发行部

电话：(010)89055541

Incremental UpdatingAlgorithm forAttribute Reduction Based on Ordered Indistinguishable String*

LIANG Baohua+,YAN Xiaoyan
College of Information Engineering,Chaohu University,Hefei 238000,China

When some new objects are added to the decision table,the attribute reduction sets will be changed.To ensure the correctness of the results,it is necessary to update the attribute reduction dynamically.Usually,the important attribute is selected which depends on the quantity of distinguishable elements in discernibility matrix algorithm. The most distinguishable information attribute is merged into reduction set every time,so the time complexity is high.Firstly,this paper proposes the definitions of effective element pair and indistinguishable string,selects the important attribute according to the length of indistinguishable string and proves the effectiveness.Secondly,this paper analyzes the different cases of added object,and updates the attribute reduction of simplified decision table according to the corresponding conditions dynamically.Then this paper designs the incremental updating algorithm based on ordered indistinguishable string.At last,the example analysis and experimental comparison show that the algorithms are feasible and effective.

attribute reduction;effective element pair;indistinguishable string;incremental updating

10.3778/j.issn.1673-9418.1602039

A

TP181

*The National Natural Science Foundation of China under Grant No.60573174(国家自然科学基金);the Outstanding Young Backbone Talent Visiting Foundation of Anhui University under Grant No.gxfx2017100(安徽省高校优秀青年骨干人才访学项目);the Natural Science Foundation ofAnhui Province under Grant No.KJ2013Z231(安徽省自然科学基金).

Received 2016-02,Accepted 2016-08.

CNKI网络优先出版:2016-08-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160801.1406.002.html

摘 要：当有新增对象加入到决策表时，已有的属性约简将会发生变化，为保证约简结果的正确性，需对其进行动态更新。差别矩阵算法通常以可区分元素的多少作为属性重要性的依据，每次选择可区分信息最多的属性加入约简集，导致有较高的时间复杂度。为此，提出了有效比较元素对及不可区分串定义，以不可区分串长短为属性重要性选择的依据，并证明了其有效性；然后分析了增量更新的不同情况，将新增对象加入简化决策表，按相应条件动态变化约简集，由此设计了基于有序不可区分串的增量更新算法；最后通过实验比较和实例分析了增量更新算法的可行性和有效性。