可靠性感知周期任务能耗管理调度算法*

张忆文，王 成

华侨大学 计算机科学与技术学院，福建 厦门 361021

可靠性感知周期任务能耗管理调度算法*

张忆文+，王 成

华侨大学 计算机科学与技术学院，福建 厦门 361021

针对EDF/DDM（earliest deadline first/dynamic deadline modify）算法不能利用空闲时间降低能耗的不足，提出了能够回收空闲时间的静态节能（static saving energy，SSE）算法。针对SSE算法没有考虑系统可靠性问题，在证明可靠性感知资源受限周期任务调度问题是NP难之后，提出两种启发式算法：最长执行时间优先算法（longest execution time first，LETF）算法和最短执行时间优先算法（shortest execution time first，SETF）算法。仿真实验表明所提出的LETF算法和SETF算法的能耗均低于EDF/DDM算法的能耗。此外，SETF算法和LETF算法的出错率比EDF/DDM算法低，是EDF/DDM算法的97%和76%，系统可靠性得到提高。

能耗；可靠性感知；资源受限；实时调度

1 引言

对于使用电池供电的嵌入式系统便捷式设备而言，低能耗是其设计目标。低能耗可以减少设备的冷却成本，延长电池的使用时间。动态电压调节（dynamic voltage supply，DVS）技术是一种有效的低功耗技术[1]，它利用系统的空闲时间，通过调节处理器速度，降低系统能耗。

低能耗调度算法是解决系统能耗的主要技术。文献[1-4]提出的算法以系统能耗为目标，忽略处理器速度对系统可靠性造成的影响。而文献[5]的研究指出，处理器速度降低，系统可靠性降低。因此，在降低处理器速度时，必须采取措施来确保系统可靠性。近年来，很多研究者针对相互独立的周期任务模型的可靠性感知调度问题开展研究[5-8]。文献[6]首次提出了可靠性感知能耗管理（reliability aware power management，RA-PM）方法来解决系统可靠性问题。该方法通过利用空闲时间构建恢复任务来确保系统可靠性。文献[9]拓展了该研究成果，并且提出了能够利用动态空闲时间构建恢复任务的方法。但是文献[9]所提的方法只能选取固定的任务作为缩放任务，对空闲时间的利用率低。文献[10]提出了能够动态利用空闲时间构建恢复任务的方法。

以上的研究成果仅仅针对相互独立的周期任务模型，忽略了系统的资源共享问题。文献[11]提出了基本的继承协议和天花板协议来解决资源共享问题。文献[12]针对资源受限的偶发任务模型，提出了EDF/DDM（earliest deadline first/dynamic deadline modify）算法来解决因资源共享所造成的优先级逆转问题。但是该算法没有考虑系统的能耗问题。文献[13]扩展了该研究成果，提出了偶发任务低功耗调度算法。该算法利用DVS技术，降低了系统能耗，但其忽略了处理器的静态功耗，且假设任务以其最坏情况下的执行时间执行。针对这些不足，张忆文等人[2]提出了考虑通用功耗模型，能够回收动态空闲时间的调度算法。但是这些研究成果都忽略了处理器速度对系统可靠性的影响。

以上研究成果仅仅针对系统可靠性、资源共享问题的某一方面进行研究，针对该问题提出了可靠性感知周期任务能耗管理调度算法。

2 系统模型和问题阐述

2.1 任务模型

在单处理器硬实时系统中，考虑n个资源限制的周期任务集T={T1,T2,…,Tn}，该任务集共享的资源集合用R={R1,R2,…,Rn}表示[11]。每个周期任务Ti用三元组(ei,ri,pi)表示，其中ei是Ti最坏情况下的执行时间；ri是Ti的资源需求，其值为1≤ri≤m之间的整数；pi是Ti的周期。ri≠0表示任务Ti在执行过程中需要使用资源Rri；ri=0表示任务Ti没有资源需求，意味着其在执行过程中不会有优先级逆转问题。系统利用率用Utot表示，其值为。假设任务Ti的相对截止期限等于其周期，且任务一次至多只使用一个资源。任务Ti的第 j个实例用Ti,j表示。

利用文献[12]提出的EDF/DDM算法调度周期任务集T。EDF/DDM算法以EDF策略为基础，通过动态地修改任务的截止期限来实现，且利用信号量确保资源能够被互斥访问。每个任务Ti有两个截止期限，初始截止期限(IDi)和执行截止期限(EDi)。IDi是根据EDF调度策略分配的截止期限，而EDi是任务开始执行时分配的截止期限。任务的优先级根据其执行截止期限来确定，执行截止期限越近，其优先级就越高，优先调度。任务Ti就绪时，设置EDi=IDi。对于有资源需求的任务Ti开始执行时修改EDi，将其值设置为。其中tri是 Ti的释放时刻；Pi是所有共享资源Ri的周期任务的最小周期，其值为Pi=min(pj|rj=i)；tsi是Ti开始执行的时刻。任务Ti的IDi=tri+pi。对于没有资源需求的任务Ti，无论何时其EDi=IDi。

2.2 功耗模型

采用系统层次的功耗模型[2]，其功耗P的计算方法如下：

其中，Ps是静态功耗，主要来自保持电路和基本时钟运转的功耗，系统关闭时其值为0；Pind是与速度无关的功耗；Cef是电路的有效负载电容；S是处理器归一化速度；m为与系统相关的常数，其值为2≤m≤3；h是常数，当处理器处于空闲状态时，其值为h=0，否则h=1。

为了使系统层次的能耗最低，文献[9]提出了关键速度Scrit的概念，为了确保任务不错过截止期限，任务的执行速度不低于关键速度Scrit。

2.3 错误模型与可靠性定义

嵌入式系统任务执行过程中存在永久错误和瞬时错误。文献[14]的研究指出，发生瞬时错误的频率远远超过永久错误，因此只考虑瞬时错误。当任务在执行过程中发生了瞬时错误，利用时间冗余的方法或重新执行任务来消除错误对系统的影响，以确保任务能够顺利地执行。假设瞬时错误可以在任务执行过程中通过一致性检查技术检测[15]，同时假设检测的开销计入任务最坏情况下的执行时间。

文献[5]的研究指出处理器速度变化会对任务的出错概率造成影响，当处理器速度降低时，任务的出错概率变大。采用文献[6-7]的任务发生错误的模型。该模型由下式给出：

其中，λ0是任务在最大处理器速度Smax下的平均出错概率，且g(Smax)=1；S是当前的处理器速度；g(S)服从指数分布，其值由下式给出:

式中，d是大于0的系统常数；Smin为处理器提供的运行速度。

文献[7]给出了任务的可靠性定义，即指任务成功执行的概率，对于任务Ti，其以速度Si执行的可靠性由下式给出：

其中，λ(Si)的值由式（2）计算。

任务Ti的原始可靠性R0i是指任务以最大的处理器速度执行的可靠性，其值为，而系统的原始可靠性是指任务集中所有任务原始可靠性的乘积，其值为。

为了确保系统可靠性，文献[7]提出RA-PM算法来解决这个问题。所谓RA-PM算法是指在降低处理器速度之前，判断此时的空闲时间是否足够构建恢复任务，以确保任务出现错误时能够重新执行该任务，恢复任务始终以最大处理器速度执行。如果空闲时间足够的话，除去构建恢复任务的时间，将余下的时间用来调节处理器速度；否则任务以最大处理器速度执行。对于任务Ti，以速度Si执行，使用RAPM算法，其可靠性由下式给出：

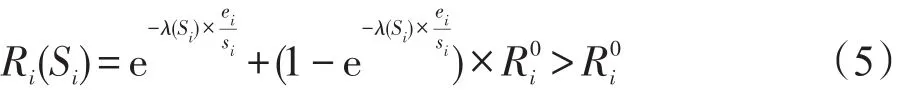
式（5）中，第一部分代表任务Ti以速度Si执行的可靠性；第二部分代表任务执行时出现错误，恢复任务执行的可靠性。从式（5）可以看出，任务的可靠性得到提高。

研究目标：针对n个有资源需求的周期任务集，在满足系统实时性、可靠性需求，确保资源被互斥使用的前提下，利用DVS技术，最大限度地降低系统能耗。

3 静态节能算法

在提出静态节能算法（static saving energy，SSE）之前，先通过一个特例，解释EDF/DDM算法存在的不足。EDF/DDM算法基于EDF算法，能够确保资源被互斥使用，但任务始终以最大的处理器速度执行。

在单处理器系统中考虑3个周期任务的任务集，每个任务的参数信息如下：

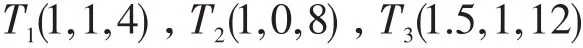
其中任务T1与任务T3共享资源R1，Utot=0.5，使用资源R1的任务的最短周期P1=4。假设所有任务都在时刻0释放，在区间[0,24]利用EDF/DDM算法调度该任务集。在时刻0，设置任务实例T1,1的ED1,1= ID1,1=4，且其在时刻1完成执行。在时刻1，任务实例T2,1没有资源需求，其ED2,1=ID2,1=5，且在时刻2完成执行。在时刻3，任务实例T3,1的ID3,1=12，且开始执行，设置ED3,1=7，在时刻3.5完成执行。其他任务实例以相似的方法调度，最终的调度结果如图1所示。

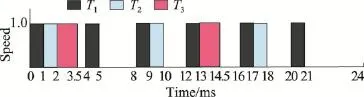
Fig.1 EDF/DDM algorithm schedules periodic task set图1EDF/DDM算法调度周期任务集

从图1可以看出，存在大量的空闲时间间隔如[4.5,8]，[10,12]，[18,20]，[21,24]等，可以利用这些空闲时间降低能耗，为此提出静态节能（SEE）算法。在介绍SSE算法之前，先介绍几个定义。

定义1有资源需求的任务集合用RT表示，值为RT={Tj|Tj∈T and rj≠0}。

定义2没有资源需求的任务集合用NRT表示，值为NRT={Tj|Tj∈T and rj=0}。

定义3在区间[0,L](Pri＜L＜pi)内，使有资源需求的集合RT中所有任务都能够满足其截止期限的最小运行速度用SRT(i)表示。

定义4在区间[0,L](Pri＜L＜pi)内，使没有资源需求的集合NRT中所有任务都能够满足其截止期限的最小运行速度用SNRT表示。

定义5资源限制的周期任务集T的最小运行速度用ST表示。

资源限制的周期任务集T被划分为两个子集RT和NRT。借鉴文献[2]的思想，计算出相应集合的最小运行速度。在集合NRT中，任务没有资源的需求，其最小的运行速度SNRT由下式计算：

文献[12]的研究指出对于有资源需求的任务Ti，在区间(Pri,pi)中必须满足以下的条件：

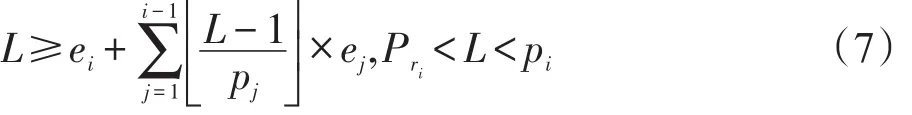
根据式（7），任务Ti的最小运行速度为SRT(i)可以通过下式计算：

有资源需求的集合RT中任务只共享一个资源时，SRT(i)是任务Ti的最小运行速度。但RT中的任务共享不同的资源时，任务Ti的运行速度应该是所有有资源需求任务的最小运行速度中的最大值。该速度用LSRT表示，其值可以由下式计算：

因此，资源限制周期任务集T的最小运行速度ST可以由下式计算：

算法1 SSE算法

（1）将资源限制周期任务集T划分为两个不相交的子集RT和NRT；

（2）计算最小运行速度ST；

（3）假如ST＜Scrit，ST=Scrit；

（4）假如任务Ti释放一个实例，根据EDF策略将其插入到就绪队列中；

（5）假如任务Ti开始执行，修改EDi；

（6）任务Ti始终以速度ST执行。

SSE算法计算ST，其时间复杂度为O(m)，而根据EDF策略将任务插入到就绪队列中，其时间复杂度为O(nlbn)。因此，SSE算法的时间复杂度为O(nlb(n+m))。

利用EDF/DDM算法的实例来解释SSE算法。该资源限制的周期任务集T被划分为RT={T1,T3}和NRT={T2}，根据式（6），SNRT=0.125；根据式（8），SRT(3)= 0.499 4；根据式（9），LSRT=0.499 4；根据式（10），ST=0.62。利用SSE算法调度任务集T的结果如图2所示。

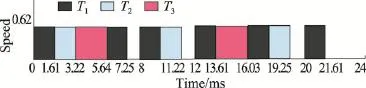
Fig.2 SSE algorithm schedules periodic task set图2 SSE算法调度周期任务集

使用文献[3]所提出的功耗模型,该功耗模型为P=0.08+1.52×S3，关键速度Scrit=0.3，处理器处于空闲状态的功耗为0.085。EDF/DDM算法调度周期任务集的总能耗为22.49，而SSE算法调度周期任务集的总能耗为8.95。因此，SSE算法比EDF/DDM算法的能耗少60.20%。

SSE算法可行的必要条件由以下的定理给出。

引理1资源限制的周期任务集T，假设周期任务的相对截止期限等于周期。SSE算法调度T是可行的，必须满足以下条件：

（1）Utot＜1；

（2）资源限制的周期任务集的最小运行速度ST满足以下条件：

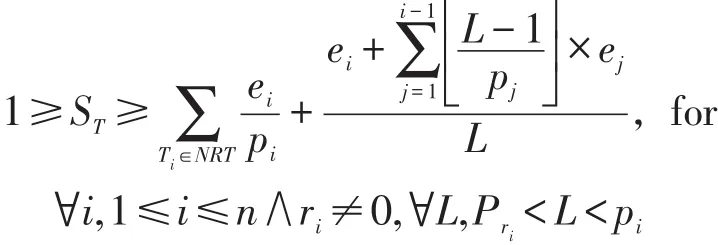
证明张忆文等人在文献[2]中给出了调度资源限制偶发任务集可行的必要条件，且给出了证明。而资源限制周期任务集是资源限制偶发任务集的特例。详细的证明过程请参见文献[2]。 □

4 两种启发式算法

SSE算法将所有的空闲时间用来降低系统能耗，没有考虑处理器速度对系统可靠性造成的影响。文献[5]的研究指出处理器速度降低时，任务的出错概率变大。在提出解决方案之前，先证明可靠性感知周期任务低能耗调度问题是NP难的。

引理2资源限制周期任务可靠性感知低能耗调度（reliability-aware low power scheduling for periodic tasks with shared resources，RMLPSR）问题是NP难的。

证明文献[7]针对共享同一截止期限的相互独立周期任务可靠性感知低能耗调度（RA-MP）问题开展研究，并且证明了该调度问题是NP难的。而RAMP是RMLPSR问题的一个特例，因此定理得证。□

考虑到RMLPSR问题是NP难的，为此提出启发式算法来解决这个问题。解决RMLPSR问题需要考虑两个问题：其一，哪些任务可以降低处理器速度（缩放任务）？其二，缩放任务的运行速度如何确定？

针对第一个问题提出两个启发式策略：其一，最长执行时间优先算法（longest execution time first，LETF），即将最坏情况下执行时间（worst case execution time,WCET）最大的任务作为缩放任务，当任务的WCET相同时，下标小的任务作为缩放任务；其二，最短执行时间优先（shortest execution time first，SETF）算法，即将WCET最小的任务作为缩放任务，当任务的WCET相同时，下标小的任务作为缩放任务。针对第二个问题，将空闲时间首先用来构建缩放任务的恢复任务（recover task，RK），余下的空闲时间用来调节处理器速度。当周期任务Ti被选为缩放任务时，空闲时间将用于构建其恢复任务RKi，剩余的空闲时间将用于调节处理器速度。恢复任务RKi的执行时间等于Ti的WCET，且其截止期限等于Ti的截止期限。为了确保系统可靠性，恢复任务始终以最大的处理器速度执行。如果此时的空闲时间不足以用来构建恢复任务RKi，缩放任务将以最大的处理器速度执行。

资源限制的周期任务集T的最小运行速度ST可以通过式（10）计算。所有的任务都以最大的处理器速度Smax(ST≤Smax)执行，这时会产生静态空闲时间。对于周期任务Ti，在此每一个调度周期内，所产生的空闲时间ST可以通过式（11）计算：

其中，EDi是任务Ti的执行截止期限；tb是周期任务Ti的释放时刻。当ST大于任务Ti的ei时，构建恢复任务RKi，余下的空闲时间ST-ei用来调节处理器速度。

LETF算法和SETF算法都是基于SSE算法，通过利用系统产生的空闲时间，构建恢复任务，确保系统可靠性，以及利用空闲时间，降低系统能耗。利用EDF/DDM算法所用的实例来解释LETF算法和SETF算法。在这个实例中，ST=0.62。LETF算法和SETF算法在区间[0,24]调度该任务集的最终调度结果分别如图3和图4所示。

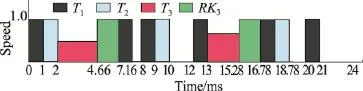
Fig.3 LETF algorithm schedules periodic task set图3 LETF算法调度任务集

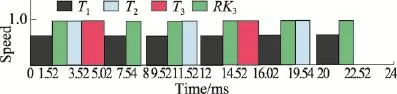
Fig.4 SETF algorithm schedules periodic task set图4 SETF算法调度任务集

在图3中，任务T3被选为缩放任务。在时刻2，任务T3的执行截止期限和释放时刻分别为7和0。因此，在第一个截止期限内可以利用的空闲时间ST为(1-0.62)×(7-0)=2.66。可以用来调节处理器速度的空闲时间为2.66-1.5=1.16。此时任务T3以速度1.5/(1.5+1.16)=0.56执行。在时刻13，任务T3的执行截止期限和释放时刻分别为18和12。因此，在第二个截止期限内可以利用的空闲时间 ST为(1-0.62)×(18-12)=2.28。可以用来调节处理器速度的空闲时间为2.28-1.5=0.78。此时任务T3以速度1.5/(1.5+0.78)=0.66执行。

在图4中，任务T1被选为缩放任务。在时刻0，任务T1的执行截止期限和释放时刻分别为4和0。因此，在第一个截止期限内可以利用的空闲时间ST为(1-0.62)×(4-0)=1.52。可以用来调节处理器速度的空闲时间为1.52-1=0.52。此时任务T1以速度1/(1+0.52)=0.66执行。在时刻5.02，任务T1的执行截止期限和释放时刻分别为8和4。因此，在第二个截止期限内可以利用的空闲时间ST为(1-0.62)× (8-4)=1.52。可以用来调节处理器速度的空闲时间为1.52-1=0.52。此时任务T1以速度1/(1+0.52)= 0.66执行。其他任务实例以相似的方法进行调度，这里不再赘述。

为了更好地评价所提出算法的性能[7]，引入以下的概念。

定义6任务Ti的原始出错概率用Fi0表示，值为。

定义7任务Ti在速度Si下的出错概率用Fi(Si)表示，值为Fi(Si)=1-Ri(Si)。

定义8资源限制的周期任务集T的原始出错概率用TF0表示，值为，其中ki为周期任务Ti的任务实例的个数。

定义9存在缩放任务的资源限制的周期任务集T的出错概率用TF表示，值为T，其中ki为周期任务Ti的任务实例的个数。

利用文献[14]的研究成果，假设λ0=10-6,d=2。通过计算可知。对于任务Ti而言，不同的实例其可靠性是不同的，简单起见，选择最小的可靠性作为这些任务实例的可靠性。在SSE算法中，通过计算可知任务T1、T2和T3的出错概率。这意味着任务T1、T2和T3的出错概率是EDF/DDM算法的相应任务出错概率的27.68倍、27.68倍和97.07倍。此外，计算出存在缩放任务的资源限制的周期任务集T的出错概率TF=45.01TF0。至此可以看出，SSE算法的出错概率是EDF/DDM算法的45.01倍，而它的能耗比EDF/DDM算法少60.22%。其他算法的能耗以及出错概率用相似的方法计算，最终的结果参见表1。

Table 1 Energy consumption and probability of failure表1 能耗与出错概率

从表1中可以看出，SETF算法的出错概率最低，且相对于EDF/DDM算法可以节约33.00%的能耗。此外，SETF算法和LETF算法的能耗都高于SSE算法的能耗，但它们的出错概率都远远低于SSE算法的出错概率。

5 仿真实验

利用C语言实现一个基于EDF/DDM调度策略的周期任务调度仿真器，该仿真器基于PXA270处理器。PXA270处理器的功耗模型[3]：P=0.08+1.52×S3，该功耗模型的关键速度Scrit=0.3，处理器处于空闲状态的功耗为0.085。在该仿真器中实现4种调度算法：（1）EDF/DDM算法，该算法所有任务都以最大处理器速度执行；（2）SSE算法，该算法基于EDF/DDM算法，且所有任务都以速度ST执行，但其忽略了速度对系统可靠性的影响；（3）LETF算法，该算法基于SSE算法，考虑了速度对系统可靠性的影响，且WCET最大的任务被选为缩放任务；（4）SETF算法，该算法基于SSE算法，考虑了速度对系统可靠性的影响，且WCET最小的任务被选为缩放任务。

以文献[16]的数控系统任务集为研究对象，该任务集包含8个周期任务，每个周期任务Ti的周期 pi在[2.4,9.6]中随机选取。为了更好地评价各个算法的性能，周期任务Ti在最坏情况下的执行时间从0.035到其周期 pi中选取。假设资源任务集有两个资源，也就是R={R1,R2}。同时假设，任务T1和任务T8共享资源R1，任务T2和任务T7共享资源R2。在每个实验中设置λ0=10-6,d=2。设置仿真实验的时间为1 000 000个时间片，每次仿真实验产生10个任务集，以这10个任务集实验结果的平均值作为最终的实验结果。在实验中任务的出错概率等于执行失败的任务的个数除以所有执行的任务的总个数。

在实验中，设置系统利用率从0.1到0.8，考察系统利用率对算法能耗和出错概率的影响。实验结果如图5和图6所示。

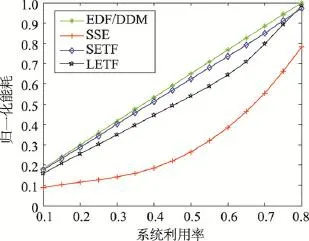
Fig.5 System utilization effects on algorithm energy consumption图5 系统利用率对算法能耗的影响

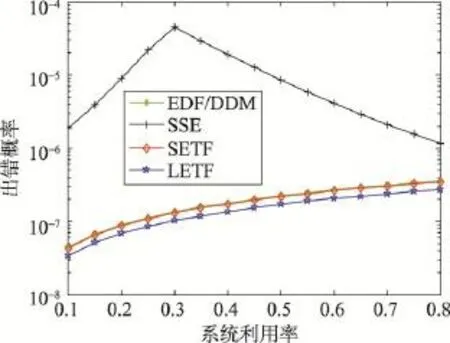
Fig.6 System utilization effects on algorithm probability of failure图6 系统利用率对算法出错概率的影响

在图5中，以EDF/DDM算法在系统利用率等于0.8时的能耗为基准进行归一化。从图5中可以看出，所有算法的归一化能耗都受到系统利用率的影响。系统利用率上升时，算法的归一化能耗也上升。这是因为系统利用率越高，任务的执行时间就越长，能耗也就增加。此外，SSE算法的归一化能耗低于其他算法的归一化能耗。这是因为该算法将所有的空闲时间用来降低系统能耗，忽略了速度对系统可靠性的影响。SETF和LETF算法的归一化能耗均低于EDF/DDM算法的归一化能耗。同时，LETF算法的归一化能耗低于SETF算法的归一化能耗。总之，SSE算法比EDF/DDM算法节约21.73%～66.36%的能耗，且SETF算法和LETF算法比EDF/ DDM算法分别节约3.61%和13.36%的能耗。

从图6中可以看出，所有算法的出错概率都受到系统利用率的影响。随着系统利用率的上升，EDF/ DDM算法、SETF算法、LETF算法的出错概率都增加。这是因为系统利用率越高，导致任务的执行时间增加，从而任务的出错概率增加。对于SSE算法而言，当系统利用率低于0.3时，出错概率上升。这是因为该算法的运行速度受到关键速度(Scrit=0.3)的限制。当系统利用率大于0.3，该算法的出错概率下降。这是因为系统利用率越高，导致任务的静态空闲时间越少，从而任务将以更高的速度运行。此外，LETF算法的出错概率总是低于SETF算法的出错概率。总之，SSE算法的出错概率是EDF/DDM算法的80.01倍，而SETF算法和LETF算法的出错概率比EDF/DDM算法低，是它的97%和76%，也就是说SETF算法和LETF算法与EDF/DDM算法相比，系统可靠性得到提高。

6 结束语

针对EDF/DDM算法存在的不足，提出能够回收空闲时间的SSE算法。针对SSE算法存在的不足，在证明可靠性感知资源受限周期任务调度问题是NP难之后，提出两种启发式算法：LETF算法和SETF算法。仿真实验表明所提算法的能耗均低于EDF/ DDM算法的能耗。此外，SETF算法和LETF算法的出错概率比EDF/DDM算法低，这意味着系统的可靠性得到提高。因为SETF算法和LETF算法假设任务始终以其最坏情况下执行时间执行，而任务真实执行时间小于其最坏情况下的执行时间，所以会产生动态空闲时间。能够回收动态空闲时间的可靠性感知资源受限周期任务动态调度算法，将是下一步的研究工作。

[1]Yao F,Demers A,Shenker S.A scheduling model for reduced CPU energy[C]//Proceedings of the 36th Annual Symposium on Foundations of Computer Science,Milwaukee,USA, Oct 23-25,1995.Piscataway,USA:IEEE,1995:374-382.

[2]Zhang Yiwen,Guo Ruifeng.Low-power scheduling algorithms for sporadic task with shared resources in hard real-time systems[J].The Computer Journal,2015,58(7):1585-1597.

[3]Chen Jianjia,Kuo Teiwei.Procrastination determination for periodic real-time tasks in leakage-aware dynamic voltage scaling systems[C]//Proceedings of the 2007 International Conference on Computer-Aided Design,San Jose,USA, Nov 5-8,2007.Piscataway,USA:IEEE,2007:289-294.

[4]Zhang Yiwen,Guo Ruifeng.A scheduling algorithm with low power for periodic tasks in hard real-time system[J]. Journal of Xi’an Jiaotong University,2014,48(7):90-95.

[5]Zhu Dakai,Melhem R,Mossé D.The effects of energy management on reliability in real-time embedded systems[C]// Proceedings of the 2004 International Conference on Computer-Aided Design,San Jose,USA,Nov 7-11,2004.Piscataway,USA:IEEE,2004:35-40.

[6]Zhu Dakai,Aydin H.Energy management for real-time embedded systems with reliability requirements[C]//Proceedings of the 2006 International Conference on Computer-Aided Design,San Jose,USA,Nov 5-9,2006.Piscataway, USA:IEEE,2006:528-534.

[7]Zhu Dakai,Aydin H.Reliability-aware energy management for periodic real-time tasks[J].IEEE Transactions on Computers,2009,58(10):1382-1397.

[8]Luo Jun,Liu Yongfeng,Fu Li.Reliability-aware schedule of periodic tasks in energy-constrained real-time systems[J]. Journal of Chongqing University,2011,34(8):86-90.

[9]Zhu Dakai.Reliability-aware dynamic energy management in dependable embedded real-time systems[C]//Proceedings of the 12th Real-Time and Embedded Technology and Applications Symposium,San Jose,USA,Apr 4-7,2006.Piscataway,USA:IEEE,2006:397-497.

[10]Zhao Baoxian,Aydin H,Zhu Dakai.Energy management under general task-level reliability constraints[C]//Proceedings of the 18th Real-Time and Embedded Technology and Applications Symposium,Beijing,Apr 16-19,2012.Piscataway,USA:IEEE,2012:285-294.

[11]Sha L,Rajkumar R,Lehoczky J P.Priority inheritance protocols:an approach to real-time synchronization[J].IEEE Transactions on Computers,1990,39(9):1175-1185.

[12]Jeffay K.Scheduling sporadic tasks with shared resources in hard-real-time systems[C]//Proceedings of the Real-Time Systems Symposium,Phoenix,USA,Dec 2-4,1992.Piscataway,USA:IEEE,1992:89-99.

[13]Huang C S,Kuo Y H,Hu J W.Scheduling sporadic,hard real-time tasks with resources[C]//Proceedings of the 3rd International Conference on Innovative Computing Information and Control,Dalian,China,Jun 18-20,2008.Piscataway, USA:IEEE,2008:84-87.

[14]Castillo X,McConnel S R,Siewiorek D P.Derivation and calibration of a transient error reliability model[J].IEEE Transactions on Computers,1982,31(7):658-671.

[15]Pradhan D K.Fault tolerance computing:theory and techniques[M].Upper Saddle River,USA:Prentice Hall,1986.

[16]Kim N,Ryu M,Hong S,et al.Visual assessment of a realtime system design:a case study on a CNC controller[C]// Proceedings of the 17th Real-Time Systems Symposium, Washington,Dec 4-6,1996.Piscataway,USA:IEEE,1996: 300-310.

附中文参考文献：

[4]张忆文,郭锐锋.硬实时系统周期任务低功耗调度算法[J].西安交通大学学报,2014,48(7):90-95.

[8]罗钧,刘永锋,付丽.能耗限制的实时周期任务可靠性感知调度[J].重庆大学学报,2011,34(8):86-90.

ZHANG Yiwen was born in 1988.He received the Ph.D.degree from University of Chinese Academy of Sciences in 2016.Now he is a lecturer at College of Computer Science and Technology,Huaqiao University,and the member of CCF.His research interests include real-time system and low-power scheduling.

张忆文（1988—），男，福建周宁人，2016年于中国科学院大学获得博士学位，现为华侨大学计算机科学与技术学院讲师，CCF会员，主要研究领域为实时系统，绿色计算。主持华侨大学科研启动项目1项，参与核高基国家科技重大专项1项、国家科技支撑计划1项，发表学术论文16篇，其中SCI/EI检索12篇，申请发明专利15项，授权2项，出版学术专著1部，获得1项软件著作权。

WANG Cheng was born in 1984.He received the Ph.D.degree in mechanics from Xi’an Jiaotong University in 2012.Now he is an associate professor and M.S.supervisor at Huaqiao University,and the senior member of CCF. His research interests include signal processing and artificial intelligence.

王成（1984—），男，湖北通城人，2012年于西安交通大学获得博士学位，现为华侨大学计算机科学与技术学院硕士生导师、副教授，CCF高级会员，主要研究领域为信号处理，人工智能。主持国家自然科学基金1项、福建省面上项目1项、华侨大学科研启动项目1项，发表学术论文20余篇。

Reliability-Aware Energy Management SchedulingAlgorithm for Periodic Task*

ZHANG Yiwen+,WANG Cheng
College of Computer Science and Technology,Huaqiao University,Xiamen,Fujian 361021,China

+Corresponding author:E-mail:zyw@hqu.edu.cn

ZHANG Yiwen,WANG Cheng.Reliability-aware energy management scheduling algorithm for periodic task. Journal of Frontiers of Computer Science and Technology,2017,11(5)：833-841.

Aiming at the shortcoming of the EDF/DDM(earliest deadline first/dynamic deadline modify)algorithm which can't use the slack time to reduce the energy consumption,this paper proposes the SSE(static saving energy) algorithm which can reclaim the slack time.But,it ignores that the processor speed has a negative effect on the system reliability.This paper proves that the problem of reliability-aware resource-constrained low-power periodic task scheduling is NP-hard.Furthermore,this paper presents two heuristic algorithms:LETF(longest execution time first)algorithm and SETF(shortest execution time first)algorithm.The simulation results show that the energy consumption of the LETF algorithm and the SETF algorithm is lower than that of the EDF/DDM algorithm.In addition, the probability of failure of the LETF algorithm and the SETF algorithm is 97%and 76%lower than that of the EDF/DDM algorithm,respectively.It means that the system reliability is improved.

energy consumption;reliability-aware;resource constrained;real-time scheduling

10.3778/j.issn.1673-9418.1609039

A

TP316.2

*The National Natural Science Foundation of China under Grant No.51305142(国家自然科学基金);the Introduction Talents Scientific Research Projects of Huaqiao University under Grant No.16BS104(华侨大学引进人才科研启动项目).

Received 2016-09,Accepted 2016-12.

CNKI网络优先出版:2016-12-07,http://www.cnki.net/kcms/detail/11.5602.TP.20161207.0922.014.html