基于三元闭包的节点相似性链路预测算法*

高 杨，张燕平，钱付兰，赵 姝

安徽大学 计算机科学与技术学院，合肥 230601

基于三元闭包的节点相似性链路预测算法*

高 杨，张燕平，钱付兰+，赵 姝

安徽大学 计算机科学与技术学院，合肥 230601

复杂网络；链路预测；三元闭包；节点权重

1 引言

很多复杂系统都可以用网络的形式来描述，节点可以表示一个人、一座城市或者一个机构等，边可以表示节点之间的联系、关系或相互作用等。复杂网络涉及的领域非常广泛，在社会、技术、生物等领域都有关于复杂网络的研究。复杂网络研究对探索网络生成机制具有重要的意义。

链路预测作为复杂网络的重要研究方向越来越受到研究者们的关注。网络中的链路预测是指如何通过已知的网络节点和网络结构等信息，预测网络中尚未连接的两个节点之间产生链接的可能性[1-3]。这种预测既包含对未知链接的预测，也包含对未来链接的预测。

链路预测问题因其重大的实际应用价值，受到不同领域不同背景的科学家的广泛关注。在生物领域研究中，例如蛋白质相互作用网络和新陈代谢网络，利用链路预测技术，可以指导其实验，降低实验成本，提高实验的成功率。在社会网络分析中遇到数据不全的情况时，链路预测同样可以作为准确分析社会网络结构的有力辅助工具[4-5]。链路预测技术可以应用于将实体及其之间关系抽象为网络的系统中，如在线社交网络、电子商务网站等，从而产生可观的商业价值。在不断发展的社交网络中，链路预测根据现有的网络结构来预测哪些尚未结交的用户“应该是朋友”，并将结果作为“朋友推荐”发给用户，可以提高相关网络在用户心目中的地位，从而提高用户对该网站的忠诚度。

本文组织结构如下：第1章介绍链路预测的研究目的与意义；第2章讨论相关工作；第3章介绍本文提出的链路预测算法；第4章给出实验结果并进行算法效率分析；第5章是结束语，总结本文工作以及对下一步研究进行展望。

2 相关工作

网络中的链路预测，既包含对未知链路的预测，也包括对未来链路的预测。基于节点相似性的链路预测方法分为3类[6]：基于网络局部结构的预测方法，基于网络全局结构的预测方法，基于准局部结构的预测方法。本文主要关注基于网络局部结构的研究。链路预测本质上是对网络演化规律的猜测。在链路预测的一些方法中体现出网络中三元闭包机制的原理。例如，共同邻居（common neighbor，CN）算法[7]，利用共同邻居节点数定义节点之间的相似性。其思想是两个节点如果有越多的共同邻居节点，那么这两个节点越相似，就越可能形成链接。Adamic等人[8]在共同邻居的基础上考虑节点的度，根据共同邻居节点的度为每个节点赋予一个权重值，提出AA（Adamic-Adar）算法。Zhou等人[9]受网络资源分配过程的启发提出了资源分配指标（resource allocation，RA）算法，与AA算法有异曲同工之效。近年来，在共同邻居的基础上结合网络拓扑结构信息的链路预测算法有很多。Gupta等人[10]认为只利用共同邻居节点的信息是不够的，在此基础上考虑非共同邻居节点之间的连接紧密程度，提出了一种新的链路预测算法，获得较好的预测效果。Yin等人[11]认为每个共同邻居节点对链接的影响是不同的，定义共同邻居节点连接强度的概念，提出了NLSA（node link strength algorithm）预测算法，并且在真实的社交网络中取得了较好预测效果。Zhang等人[12]在考虑两步路径上的节点对链接产生贡献的同时又考虑了三步路径上节点的贡献，提出了CCN（cohesive common neighbors）算法，并且取得了较高的预测精确度。利用三元闭包机制结合网络拓扑结构信息可以提高链路预测算法的预测效果。

三元闭包（triadic closure）[13]作为网络最基本的局部结构和重要的链接生成机制，在网络模型的研究中不断被提到，对探索网络演化机制具有重要的作用。其作为网络中的最小局部结构，具有结构平衡和稳定的特征。三元闭包的形成机理在不同的网络中有着不同的解释。在朋友网络中表现为：A和B是朋友，B和C也是朋友，那么A和C很可能也是朋友。在微博中关注关系网络中表现为：关注用户v的用户u同时关注了很多v的朋友，那么u很可能去关注用户v关注的用户。文献[14]在Twitter上的朋友推荐系统的研究中，根据三元闭包的形成机理，利用HITS算法与根据该机理计算得到的用户间的相似性值来产生最后的推荐结果，并获得了不错的效果。文献[15]提到三元闭包的形成过程是多种网络中新链接生成的一个非常重要的机制，并在引文网络中证明了该机制是引文链接产生的重要力量。文献[16]提出一种基于三元闭包机制的网络生长模型，利用该模型产生带有肥尾分布、高聚类系数和强社团结构特征属性的网络系统，体现出三元闭包在网络演化中的重要作用。文献[17]根据三元闭包定义聚类系数的思想，在双模网络中重新定义了聚类系数的计算方法，体现出三元闭包在不同网络中的应用。文献[18]根据三元闭包和随机链接两种机制，提出了一种社交网络增长模型，并应用到两种社交网络中，证明了该模型能够重建网络的主要拓扑结构。另外文献[19]研究在动态网络中三元闭包是如何形成的，提到三元闭包预测问题与链路预测是相关的，不同之处是它只专注于预测三元闭包中的链路问题。

本文根据三元闭包结构提出了一种加节点权重的链路预测算法，根据三元闭包结构的数目计算节点的权重。首先统计网络中每个节点拥有的三元闭包结构的数目，根据该数目对每个节点排序，得到每个节点的序值，再将序值映射到区间[0,1]内，由此求得每个节点的权重。将其应用到节点相似性指标中得到计算相似性的方法。采用CN算法、AA算法和RA算法作为最基本的对比算法。与文献[20]和文献[21]中提出的在有权网络中的链路预测算法进行比较，在10个真实网络中实验结果表明，本文算法能够提高链路预测的精确度。分析实验结果，发现了一个很有趣的现象：在社交网络中，拥有较多三元闭包结构的用户，不倾向于建立更多的新链接；相反，拥有较少三元闭包结构的用户，倾向于建立更多的新链接。这种现象也符合社会学中有关弱关系产生链接的现象。

3 算法描述

3.1 链路预测问题描述

定义一个无向网络G(V，E)，其中V表示节点集合，E表示边的集合。网络总的节点数是N，总的边数是M。令U为N×(N-1)/2个节点对组成的全集。给定一种链路预测方法，为每对没有连边的节点对(x,y)赋予一个分数值。这个分数值可以理解为一种接近性，它与两节点的链接概率正相关。将所有未连接的节点对按照该分数值从大到小排序，排在最前面的节点对相互连接的概率最大。

3.2 基本算法介绍

定义Γ(x)表示节点x的邻居节点集合，CN、AA、RA算法的计算节点相似性指标的定义如下。

（1）CN指标：其思想是两个节点如果有很多的共同邻居节点，那么这两个节点相似。

（2）AA指标：其思想是度小的共同邻居节点的贡献大于度大的共同邻居节点，根据共同邻居节点的度为每个节点赋予一个权重值。

（3）RA指标：其思想是每个媒介都有一个单位的资源并且将平均分配传给它的邻居，则节点可以接收到的资源数就定义为节点x和y的相似性。

其中，kz表示节点z的度。

3.3 基于三元闭包的链路预测算法

三元闭包作为网络最基本的局部结构和重要的链接生成机制，对网络衍化有着重要的作用。作为网络中的最小局部结构，具有结构平衡和稳定的特征。可以将其应用到链路预测当中，探索其对网络衍化的影响。用一个三元组表示一个三元闭包，即(A，B，C)，其表示在网络中的结构是节点A与节点B和C都有连边，且节点B和C之间也有连边。统计整个网络中的三元闭包数目，根据这些存在的三元闭包统计出每个节点所拥有的三元闭包的数目。在网络中，节点拥有的三元闭包越多，它的聚类系数可能越大，它的“朋友圈”就越紧密，该节点就越重要。为了量化这种重要性，采用如下的做法：统计网络中节点i拥有的三元闭包数目nΔi，对nΔi进行排序，nΔi越大，序值x越小，节点就越重要。根据函数 f(x)= 1/(1+lg x)，将序值映射到[0,1]之间，得到最终的节点权重wi。一个简单的例子如图1所示。在该网络中，三元闭包结构中的边用粗黑线表示，非三元闭包结构中的关系用细黑线表示，该简单网络中的三元闭包结构有(1,2,9)、(1,2,7)、(1,7,9)、(2,3,9)、(2,7,9)、(4, 5,7)。节点权重的计算结果如表1所示。

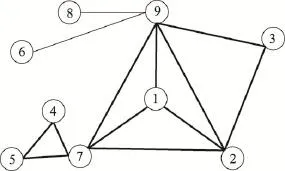
Fig.1 Asimple network图1 一个简单网络

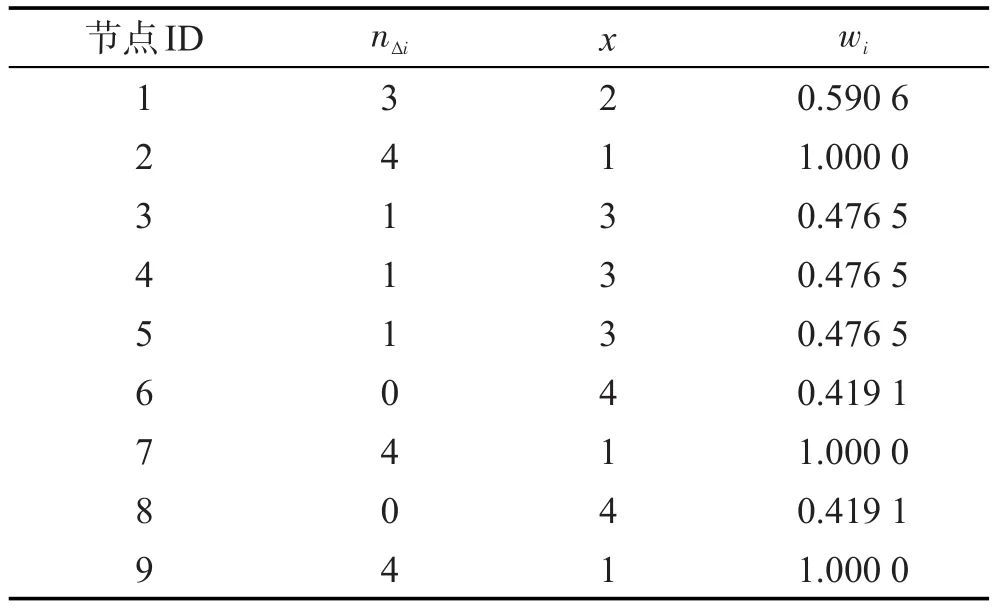
Table 1 Node weight表1 节点权重

基于三元闭包的节点相似性链路预测算法，其计算相似性的方法是将所求的节点权重应用到CN指标、AA指标和RA指标中，分别得到加节点权重的共同邻居指标TWCN，加节点权重的Adamic-Adar指标TWAA，加节点权重的资源分配指标TWRA。其计算公式如下所示：

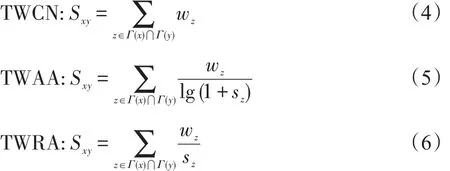
为了进一步研究三元闭包结构在链路预测中的作用，将式（4）、（5）和（6）节点相似性指标进行改进，加入权重调节参数α来调节权重的大小。其计算公式如下所示：

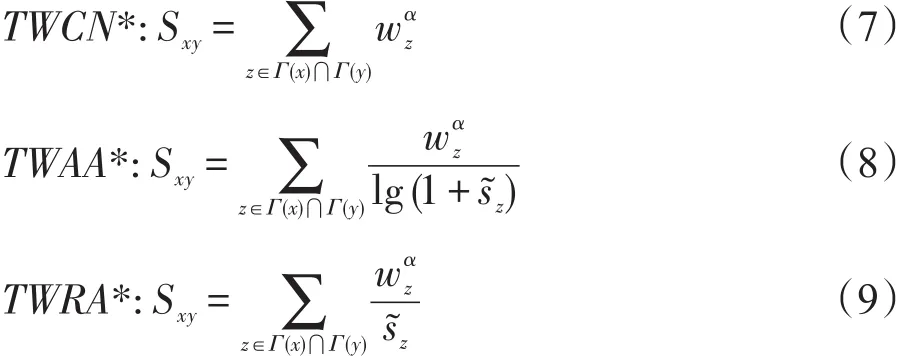
将根据三元闭包计算节点权重的算法命名为CNWTC（calc node weight based triadic closure）算法。将基于节点权重的链路预测算法命名为PWNW（prediction with node weight）算法。将带调节参数α的链路预测算法命名为PWNW_α（prediction with node weight_α）算法。

算法1 CNWTC算法

算法2 PWNW算法

算法3 PWNW_α算法

4 实验结果分析

4.1 评价指标

链路预测评价指标有AUC（area under the receiver operating characteristic curve）[22]和精确度[23]precision）。

AUC可以理解为在测试集中的边的分数值有比随机选择的一条不存在的边的分数值高的概率。独立比较n次，如果有n′次测试集中的边的分数值大于不存在的边的分数值，有n″次两分数值相等，其计算公式如下所示：

precision定义为在前L个预测边中被预测准确的比例。如果有m个预测准确，即排在前L的边中有m个在测试集中，则precision定义为：

本文采用的评价指标是precision，排序列表L的长度为100。

4.2 实验数据

本文采用10个真实网络数据集，分别是以复杂网络为主题发表过论文的科学家合作网络[24]Net-Science）、计算几何领域的科学家合作网络（CGScience，http://vlado.fmf.uni-lj.si/pub/networks/data/）、爵士音乐家合作网络[25]Jazz）、Facebook（http://snap.stanford. edu/data/）社交网络，以及6个合作者网络（T75sub0、T162sub1、T145sub0、T131sub0、T24sub0、T107sub1，http://www.datatang.com/datares/go.aspx?dataid=608815）。数据集详细信息如表2所示（表中N表示节点数，M表示边数，＜k＞表示网络的平均度，＜c＞表示网络的平均聚类系数，D表示网络密度，Triadic表示网络中三元闭包数目）。另外还分析了节点的度和节点拥有的三元闭包数的关系，如图2所示（图中的横坐标表示节点的度d，纵坐标表示度为d的节点拥有的三元闭包数目的平均数）。从图中的结果可以看出，整体上，节点的三元闭包数正比于节点的度。即节点的度越大，该节点拥有的三元闭包的数目就越多。另外，图中随着度的增加散点的分布越稀疏，这是因为网络中度越大，节点的数目越少。由图2的结果还可以看出，度大的节点占据着网络中大部分三元闭包结构，由此看出度大的节点对网络结构稳定性有着重要影响。

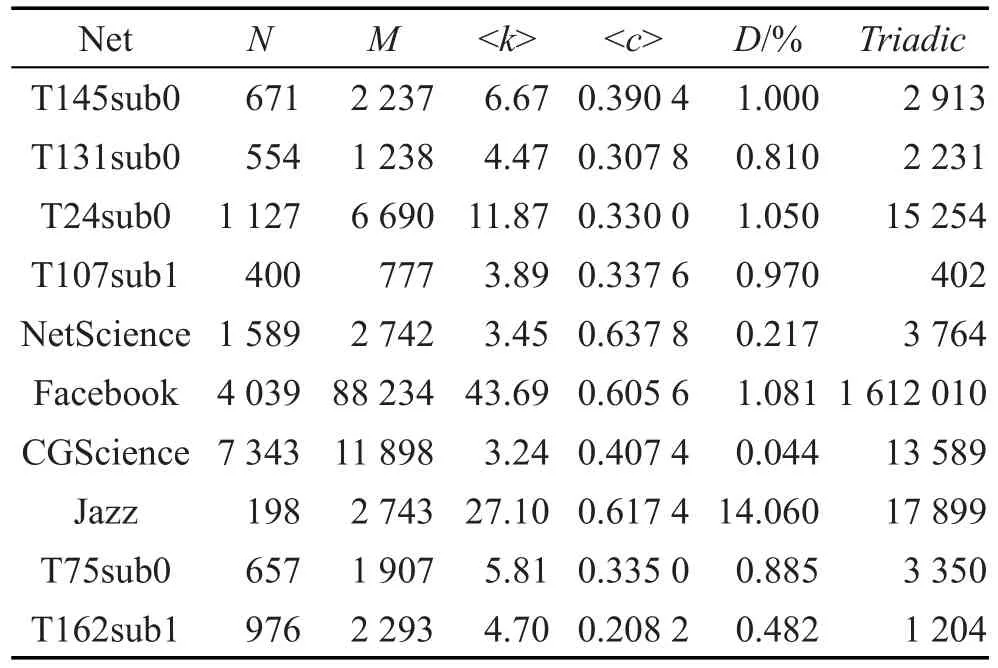
Table 2 Information of datasets表2 数据集信息

4.3 结果分析

本文采用十字交叉验证法，将数据集平均分为10份，其中1份作为测试集，其余9份作为训练集。分别进行了10次实验，取平均值作为最后的结果。与基本算法的精确度比较结果如表3所示，在该表中CN、AA、RA对应的结果是基本相似性指标算法的精确度结果；TWCN、TWAA、TWRA对应的结果是直接加上节点权重的相似性指标的精确度结果（即PWNW算法的结果）；TWCN*、TWAA*、TWRA*对应的结果是在最优参数α时的加节点权重的相似性指标的精确度结果（即PWNW_α算法的结果）。表3～表5中加黑字体表示在对应指标下的最优精确度值。

另外从表4可以得到，由结构信息获得的节点权重的链路预测算法在部分网络中的预测效果，仍然高于由一般属性信息获得的边权重的链路预测算法的预测效果。表5比较了有权重参数α调节的两种不同权重预测算法的预测结果，可以看出，由结构信息获得的节点权重链路预测算法（PWNW_α算法）仍有预测精度上的优势。

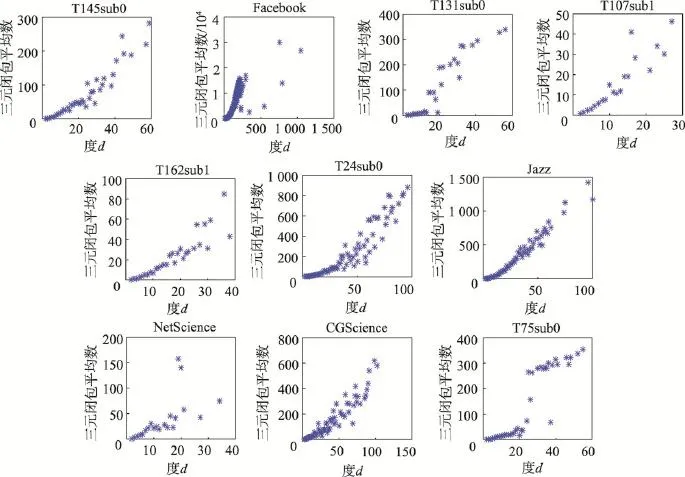
Fig.2 Relationships between the number of triadic closure and degree d图2 三元闭包数与度d的关系

而且本文算法的相似性指标是基于网络结构信息的，其适用范围比较广泛，在有权网络和无权网络中均可应用。整体来说，该相似性指标在无权网络中能够提高预测精确度，在有权网络中，该算法的精确度亦可以得到保证。图3给出在这10个不同网络中精确度与权重调节参数α的关系。根据精确度与α的关系，获得各指标取得最优值时α的取值情况，来进一步研究三元闭包对链路预测精确度的影响。参数α的取值结果如表6所示。

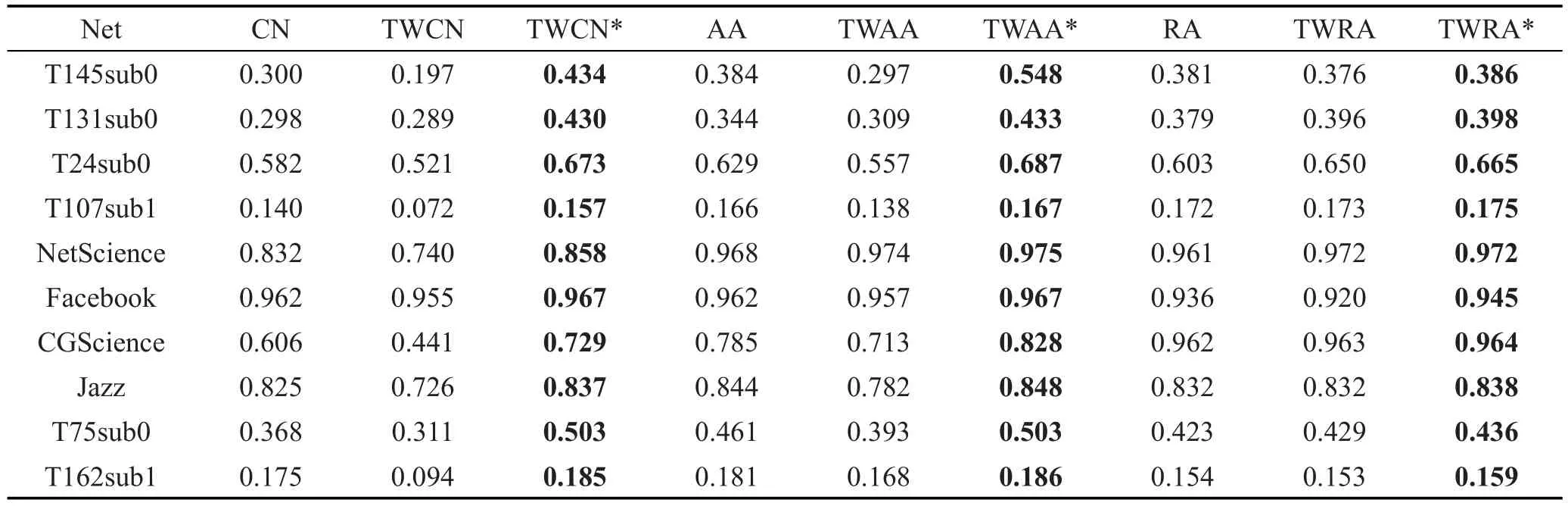
Table 3 Precision of CNWTC,PWNA_αand CN,AA,RAalgorithms表3 CNWTC算法、PWNA_α算法与CN、AA、RA算法的精确度

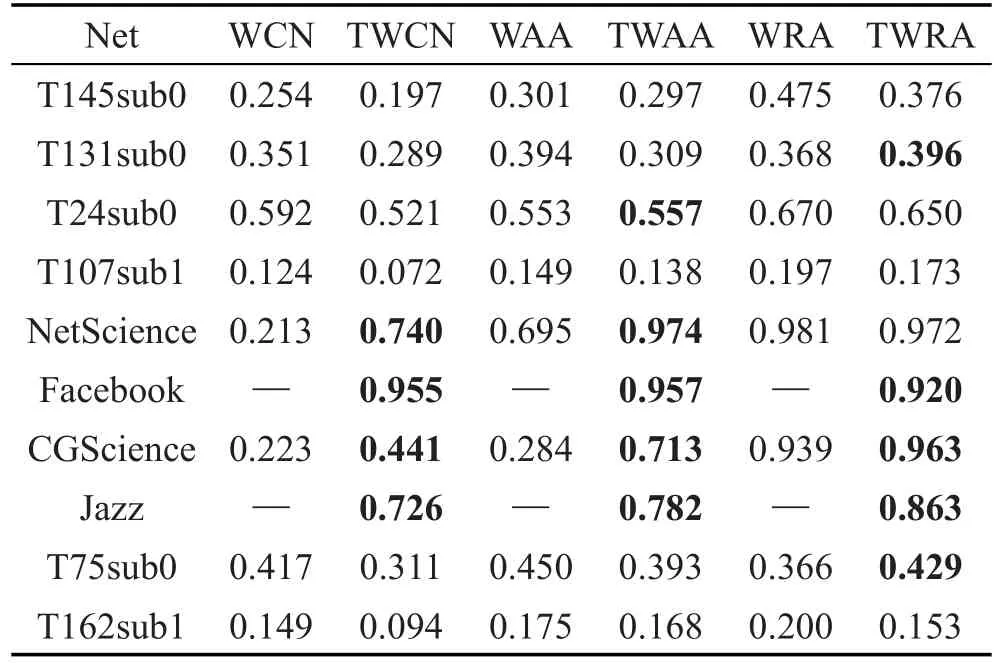
Table 4 Precision of TWCN,TWAA,TWRA and WCN,WAA,WRA表4 TWCN、TWAA、TWRA与WCN、WAA、WRA的精确度

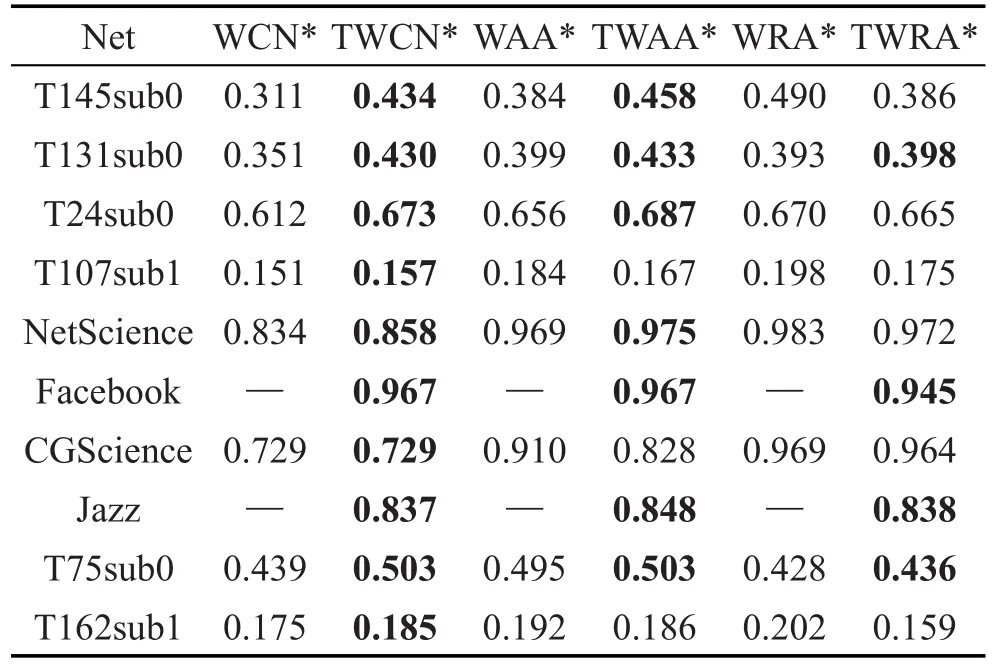
Table 5 Precision of TWCN*,TWAA*,TWRA* and WCN*,WAA*,WRA*表5 TWCN*、TWAA*、TWRA*与WCN*、WAA*、WRA*的精确度

当最优参数α的值均小于0时，基于三元闭包得到的节点权重，权重小的节点对预测精确度的促进作用较大，而权重较大的节点对预测精确度的促进作用较小。这说明在社交网络中会有这样一种现象：拥有较多三元闭包的节点不倾向于建立更多的新链接；相反，拥有较少三元闭包的节点非常乐意去建立更多的新链接。即朋友圈越紧密的人不倾向结交更多的新朋友。在社会学领域中弱关系传递信息，人们为了获取更多且有用的信息，往往会愿意和关系并不紧密的朋友建立联系。本文所提算法的实验结果也契合了这种社会学现象。表6中α取负值的情况（表6中加黑字体所示），说明这种现象是存在于社交网络中的。

为了进一步分析实验结果，做出如下定义：如果一条边所在的三元闭包数目大于3，说明这条边具有局部结构特征。假设一条边只具有局部结构特征和非局部结构特征，得到如图4所示的结构（粗线表示一条边只具有局部结构特征）。网络中的三元闭包结构可以表示为图5中所示结构。

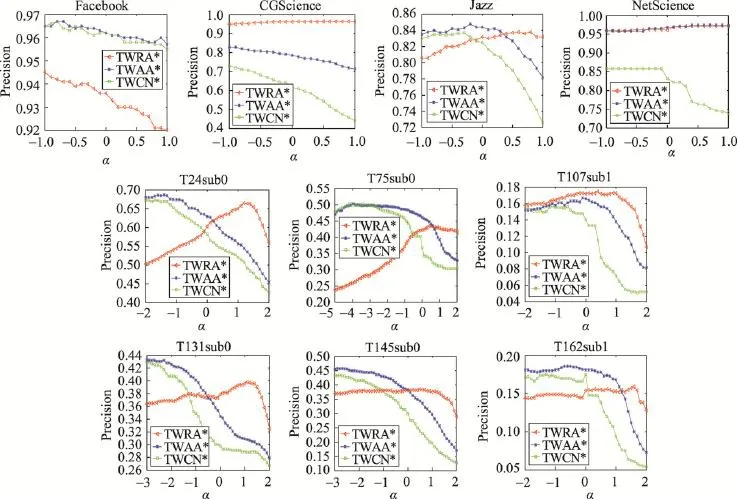
Fig.3 Relationships between precision and parameterα图3 精确度与参数α之间的关系

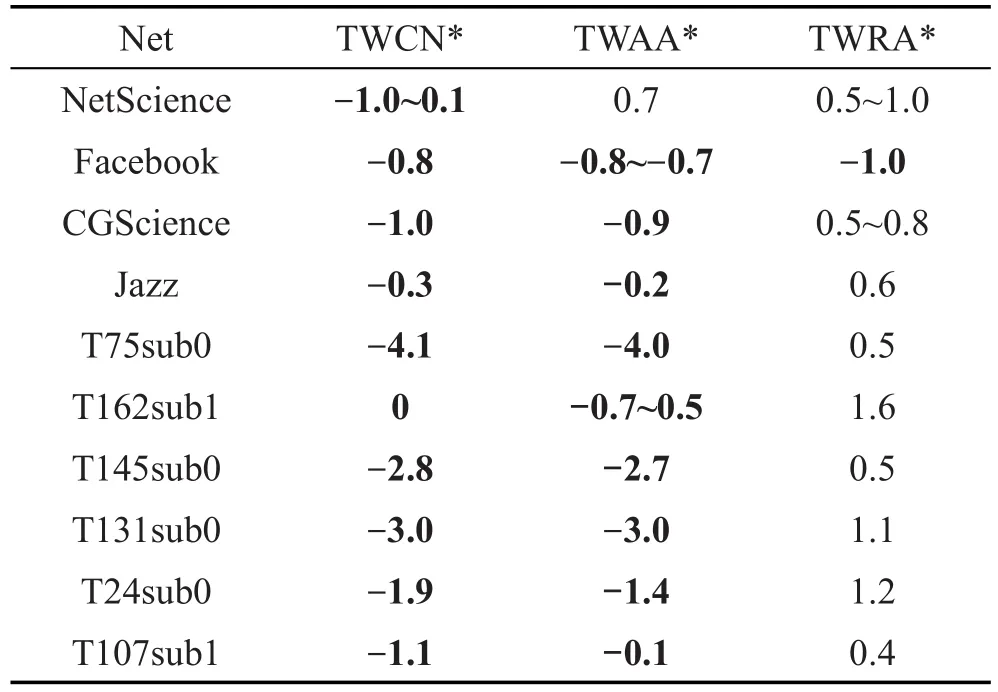
Table 6 Values of optimal parameterα表6 最优参数α取值情况

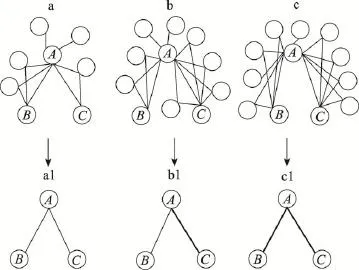
Fig.4 Structure feature of edge in network图4 网络中边的结构特征

在这10个网络中统计这7种连通三元闭包CS1～CS7的数目，分别用N1～N7表示。那么两条边都具有局部结构特征，则相连的概率就为。设参数 β=N4/Triadic（Triadic表示网络中三元闭包数目）。β越大，说明网络的局部结构越稠密，三元闭包数越多。P1越小，说明网络中局部相连的概率越低。当β越大P1越小时，说明网络的局部结构越稠密，但是局部结构相连的概率越低，该结果正好反映出上述现象。该结果越明显说明这种现象在网络中表现就越明显。从表7的结果中可以看出，Facebook、Jazz、T75sub0、T145sub0、T131sub0和T24sub0这6个网络明显具有这种特征，这同样说明了该现象是明显存在于部分社交网络中的。

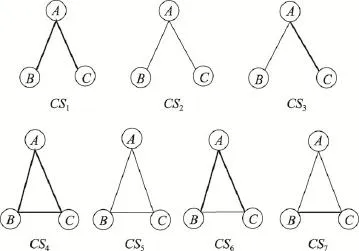
Fig.5 Triadic closure structure in network图5 网络中三元闭包结构

Table 7 Values ofP1andβ表7 P1与 β值

4.4 算法时间复杂度分析

运算效率高且预测效果好的链路预测算法较难获得，一般的算法是在两者之间取得一个平衡或谋求某一方面的促进与提升。在基于共同邻居的链路预测算法中，计算节点对的共同邻居的时间复杂度为O(k)，k表示网络的平均度。因此对于CN算法来说，计算所有节点的相似度值的时间复杂度为O(n2×k)。AA与RA两个算法与CN算法有着相同的计算过程，同样与CN算法的时间复杂度也相同。较为简单的PA算法[7]，其时间复杂度为O(n2)，是一种较为高效的方法。另外，局部路径指标LP算法[26]的时间复杂度为O(n×k3)。基于全局的预测算法Katz[27]的时间复杂度为O(n3)，另外ACT[28]和RWR[29]算法的时间复杂度也是O(n3)。基于随机游走的两个算法LRW和SRW[30]的时间复杂度为O(n×kl)，其中l为随机游走的步数。本文算法最耗时的地方是统计网络中三元闭包数目的过程，其时间复杂度为O(n3)。其预测过程与CN算法的预测过程是完全相同的，该过程的时间复杂度为O(n2×k)，因此本文算法的时间复杂度为O(n3)。与CN、AA、RA算法相比牺牲了时间换取精度上的提升。

5 结束语

本文提出了一个新的基于网络局部拓扑结构的度量节点相似性的链路预测算法。利用了网络中的最基本的局部结构三元闭包，根据结构平衡理论，三元闭包具有结构平衡特征和稳定性特征。通过统计网络中三元闭包数目，经过转化得到节点权重，将该权重应用到链路预测相似性指标中，得到计算节点相似性的方法，即3个相似性指标TWCN、TWAA、TWRA和具有调节参数α的3个相似性指标TWCN*、TWAA*、TWRA*，由此提出PWNW算法和PWNW_ α算法。与CN、AA和RA算法相比，PWNW_α算法在预测效果上有很大的优势。在10个网络数据集上的实验结果表明，本文提出的链路预测算法能够提高预测精确度。通过分析参数α的结果得到了一个很有趣的现象：在社交网络中，拥有较多三元闭包的节点，不倾向于建立更多的新链接；相反，拥有较少三元闭包的节点，乐于建立更多的新链接。这种现象也符合社会学中有关弱关系产生链接的现象。

无向网络中的一个三元闭包，在有向网络中有7种情形。有向网络中的三元闭包比无向网络更复杂，不同的三元闭包对网络功能有着不同的影响。下一步的工作是研究不同形式的三元闭包对有向网络链路预测算法的影响。

[1]Mamitsuka H.Mining from protein-protein interactions[J]. Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery,2012,2(5):400-410.

[2]Aiello L M,BarratA,Schifanella R,et al.Friendship prediction and homophily in social media[J].ACM Transactions on the Web,2012,6(2):1-33.

[3]Getoor L,Diehl C P.Link mining:a survey[J].ACM SIGKDD Explorations Newsletter,2005,7(2):3-12.

[4]Lv Linyuan,Zhou Tao.Link prediction in complex networks: a survey[J].Physica A:Statistical Mechanics and Its Applications,2011,390(6):1150-1170.

[5]Lv Linyuan.Link prediction on complex networks[J].Journal of University of Electronic Science and Technology of China,2010,39(5):651-661.

[6]Chen Bolun,Chen Ling,Li Bin.A fast algorithm for predicting links to nodes of interest[J].Information Sciences,2016, 329:552-567.

[7]Xie Yanbo,Zhou Tao,Wang Binghong.Scale-free networks without growth[J].Physica A:Statistical Mechanics and Its Applications,2008,387(7):1683-1688.

[8]Adamic L A,Adar E.Friends and neighbors on the Web[J]. Social Networks,2003,25(3):211-230.

[9]Ou Qing,Jin Yingdi,Zhou Tao,et al.Power-law strengthdegree correlation from a resource-allocation dynamics on weighted networks[J].Physical Review E,2007,75:021102.

[10]Gupta N,Singh A.A novel strategy for link prediction in soial networks[C]//Proceedings of the 10th International Conference on Emerging Networking Experiments and Technologies on Student Workshop,Sydney,Dec 2-5,2014. New York:ACM,2014:12-14.

[11]Yin Guisheng,Yin Wansi,Dong Yuxin.A new link prediction algorithm:node link strength algorithm[C]//Proceedings of the 2014 IEEE Symposium on Computer Applications and Communications,Weihai,China,Jul 26-27,2014. Piscataway,USA:IEEE,2014:5-9.

[12]Zhang Weiyu,Wu Bin.Accurate and fast link prediction in complex networks[C]//Proceedings of the 10th International Conference on Natural Computation,Xiamen,China,Aug 19-21,2014.Piscataway,USA:IEEE,2014:653-657.

[13]Easley D,Kleinberg J.Networks,crowds,and markets:reasoning about a highly connected world[M].Cambridge,UK: Cambridge University Press,2010.

[14]Carullo G,Castiglione A,De Santis A,et al.A triadic closure and homophily-based recommendation system for online social networks[J].World Wide Web,2015,18(6):1579-1601.

[15]Peng Taiquan.Assortative mixing,preferential attachment, and triadic closure:a longitudinal study of tie-generative mechanisms in journal citation networks[J].Journal of Informetrics,2015,9(2):250-262.

[16]Bianconi G,Darst R K,Iacovacci J,et al.Triadic closure as a basic generating mechanism of communities in complex networks[J].Physical Review E,2014,90(4):042806.

[17]Opsahl T.Triadic closure in two-mode networks:redefining the global and local clustering coefficients[J].Social Networks,2013,35(2):159-167.

[18]Medus A D,Dorso C O.Triadic closure mechanism in faceto-face and online social relationship networks[J].arXiv: 1312.3496,2013.

[19]Huang Hong,Tang Jie,Wu Sen,et al.Mining triadic closure patterns in social networks[C]//Proceedings of the 23rd International Conference on World Wide Web,Seoul, Apr 7-11,2014.New York:ACM,2014:499-504.

[20]Lv Linyuan,Zhou Tao.Role of weak ties in link prediction of complex networks[C]//Proceedings of the 1st ACM International Workshop on Complex Networks Meet Information&Knowledge Management,Hong Kong,China,Nov 6,2009.New York:ACM,2009:55-58.

[21]Wind D K,Mørup M.Link prediction in weighted networks [C]//Proceedings of the 2012 International Workshop on Machine Learning for Signal Processing,Santander,Spain, Sep 23-26,2012.Piscataway,USA:IEEE,2012:1-6.

[22]Hanley J A,McNeil B J.The meaning and use of the area under a receiver operating characteristic(ROC)curve[J]. Radiology,1982,143(1):29-36.

[23]Herlocker J L,Konstan J A,Terveen L G,et al.Evaluating collaborative filtering recommender systems[J].ACM Trans-actions on Information Systems,2004,22(1):5-53.

[24]Newman M E J.Finding community structure in networks using the eigenvectors of matrices[J].Physical Review E, 2006,74(3):036104.

[25]Gleiser P M,Danon L.Community structure in Jazz[J].Advances in Complex Systems,2003,6(4):565-573.

[26]Zhou Tao,Lv Linyuan,Zhang Yicheng.Predicting missing links via local information[J].The European Physical Journal B,2009,71(4):623-630.

[27]Katz L.A new status index derived from sociometric analysis[J].Psychometrika,1953,18(1):39-43.

[28]Klein D J,Randić M.Resistance distance[J].Journal of Mathematical Chemistry,1993,12(1):81-95.

[29]Sehgal U,Kaur K,Kumar P.The anatomy of a large-scale hyper textual Web search engine[C]//Proceedings of the 2nd International Conference on Computer and Electrical Engineering,Dubai,UAE,Dec 28-30,2009.Washington: IEEE Computer Society,2009:491-495.

[30]Liu Weiping,Lv Linyuan.Link prediction based on local random walk[J].Europhysics Letters,2010,89(5):58007.

附中文参考文献：

[5]吕琳媛.复杂网络链路预测[J].电子科技大学学报,2010, 39(5):651-661.

GAO Yang was born in 1990.He is an M.S.candidate at Anhui University.His research interests include complex network and link prediction,etc.

高杨（1990—），男，安徽宿州人，安徽大学硕士研究生，主要研究领域为复杂网络，链路预测等。

ZHANG Yanping was born in 1962.She is a professor and Ph.D.supervisor at Anhui University,the member of CCF.Her research interests include intelligent computing,quotient space,machine learning,artificial neural network and intelligent information processing,etc.

张燕平（1962—），女，安徽合肥人，安徽大学教授、博士生导师，CCF会员，主要研究领域为智能计算，商空间，机器学习，神经网络，智能信息处理等。发表学术论文80多篇，其中SCI、EI、ISTP收录30多篇。

QIAN Fulan was born in 1978.She received the Ph.D.degree from Anhui University in 2016.Now she is a lecturer at Anhui University,and the member of CCF.Her research interests include granular computing,social network and data mining,etc.

钱付兰（1978—），女，安徽蚌埠人，2016年于安徽大学获得博士学位，现为安徽大学讲师，CCF会员，主要研究领域为粒计算，社交网络，数据挖掘等。

ZHAO Shu was born in 1979.She is a professor and Ph.D.supervisor at Anhui University,and the member of CCF.Her research interests include intelligent computing,quotient space,machine learning,social network and granular computing,etc.

赵姝（1979—），女，安徽合肥人，安徽大学教授、博士生导师，CCF会员，主要研究领域为智能计算，商空间，机器学习，社交网络，粒计算等。

Link PredictionAlgorithm Based on Node Similarity of Triadic Closure*

GAO Yang,ZHANG Yanping,QIAN Fulan+,ZHAO Shu
School of Computer Science and Technology,Anhui University,Hefei 230601,China

+Corresponding author:E-mail:qianfulan@hotmail.com

GAO Yang,ZHAGN Yanping,QIAN Fulan,et al.Link prediction algorithm based on node similarity of triadic closure.Journal of Frontiers of Computer Science and Technology,2017,11(5)：822-832.

Link prediction is a fundamental method for analyzing complex network which has been widely used in many domains.Link prediction in complex network based on solely topological information is a challenging problem.As one of the basic local structure,triadic closure has the characteristics of structural balance and stability.This paper proposes a link prediction algorithm to measure the similarity of nodes based on triadic closure.By calculating the weight of each node in the network according to the triadic closure,and using the weights in the node similarity index,this paper proposes three similarity indexes of TWCN,TWAA,TWRA and the other three similarity indexes of TWCN*,TWAA*,TWRA*with adjustment parameter.The experimental results on ten real network datasets demonstrate that the new method can improve the accuracy of link prediction.Moreover,by analyzing the experiment results,this paper finds that the network with more triadic closure nodes tends to be more stable.In other words,a network with less triadic closure nodes is less stable,and it is more likely to establish a new link with others.This phenomenon is also consistent with some related phenomenon in sociology on weak relations to generate links.

complex networks;link prediction;triadic closure;node weight

10.3778/j.issn.1673-9418.1605039

A

TP391

*The National Natural Science Foundation of China under Grant Nos.61175046,61402006(国家自然科学基金);the Natural Science Foundation of Anhui Province under Grant No.1508085MF113(安徽省自然科学基金);the Humanities and Social Science Foundation of the Ministry of Education of China under Grant No.1508085MF113(教育部人文社科基金项目).

Received 2016-04,Accepted 2016-06.

CNKI网络优先出版:2016-06-23,http://www.cnki.net/kcms/detail/11.5602.TP.20160623.1139.008.html

摘 要：链路预测作为复杂网络分析的基本方法被应用到很多领域，完全基于拓扑结构信息的复杂网络链路预测仍然是一个具有挑战性的问题。三元闭包作为网络中最小局部结构，具有结构平衡和稳定的特征。提出了一种基于三元闭包的节点相似性链路预测算法，通过计算出每个节点在网络中所占三元闭包的权重，并将该权重用于节点相似性指标中，提出了3个相似性指标TWCN、TWAA、TWRA和具有调节参数的3个相似性指标TWCN*、TWAA*、TWRA*。在10个不同的网络数据集上的实验结果表明，所提算法能够提高链路预测的精度。不仅如此，通过分析实验结果，发现在社交网络中拥有较多三元闭包的节点具有局部稳定性，不倾向于建立更多的新链接；相反，拥有较少三元闭包的节点具有局部不稳定性，倾向于建立更多的新链接。这种现象也符合社会学中有关弱关系产生链接的现象。