隐子空间聚类算法的改进及其增量式算法*

董 琪，王士同

江南大学 数字媒体学院，江苏 无锡 214122

隐子空间聚类算法的改进及其增量式算法*

董 琪+，王士同

江南大学 数字媒体学院，江苏 无锡 214122

基于稀疏表示的隐子空间聚类（latent subspace clustering，LSC）算法，相对于传统的子空间聚类算法，具有更快的聚类速度，使其适用于更大的数据集，但是其存在字典训练具有随机性，占用内存过多等缺陷。参照LC-KSVD字典训练算法的思想，通过将一部分信号的标签信息添加进字典训练阶段，以此提高了字典的判别性，进而提出了聚类精度更好的ILSC（improved LSC）算法。但相比于LSC算法，ILSC算法在字典训练阶段的耗时却大幅增加，针对此缺陷，参照增量字典训练的思想，提出了ILSC算法的增量式聚类算法I2LSC（incremental ILSC），在确保聚类精度、NMI（normalized mutual information）、RI（Rand index）值高于LSC且与ILSC相当的同时，较之ILSC具有更快的运行速度。

子空间聚类；隐子空间聚类（LSC）；判别式字典训练；增量式字典训练

1 引言

聚类分析是数据挖掘、模式识别领域的重要内容。随着数据维度的增大，高维数据的聚类成为聚类分析技术的重点和难点，子空间聚类是实现高维数据集聚类的一种有效途径，它是根据一簇信号集的子空间跨越情况来进行聚类的算法，是对传统聚类算法的一种扩展。根据文献[1]，子空间聚类算法可以根据实现方法分为4类，即基于统计的方法、代数的方法、迭代的方法和基于谱聚类的方法。现阶段最流行的算法包括：Elhamifar等人基于一维稀疏性提出的稀疏子空间聚类算法（sparse subspace clustering，SSC）[2]，Liu等人进一步利用二维稀疏性提出的基于低秩表示的子空间聚类算法（low-rank representation，LRR）[3]，Favaro等人提出的基于低秩表示的闭合解子空间聚类算法（closed form solutions of low-rank representation，LRR-CFS）[4]，这些算法都基于谱聚类，并拥有优秀的聚类性能。LRR和SSC是相似的算法，都是通过构建自表示系数矩阵来展现初始信号间的相关性，并利用系数矩阵构建相似度矩阵，最后利用谱聚类算法如Ncut[5]得到最终的聚类结果。但是由于系数矩阵计算的多项式复杂度和聚类时的复杂度，限制了它们只能处理中小规模数据集。文献[6]提出了一种基于稀疏表示的隐子空间聚类（latent subspace clustering，LSC）算法，其稀疏表示系数矩阵是通过OMP（orthogonal matching pursuit）[7]算法构建而来，有效降低了系数矩阵计算和聚类时的复杂度。LSC算法中使用K-SVD[8]算法训练出一个所有类共享的字典。该字典虽然具有优秀的重构能力，但是缺乏足够的判别信息，导致系数矩阵表示的数据与原始信号之间存在较大的误差，故会影响LSC算法的聚类精度。

针对以上问题，人们改进了LSC算法的字典训练过程，Zhang等人[9]基于K-SVD算法引入监督学习的思想，提出了一种判别式字典训练算法D-KSVD（discriminative K-SVD），通过同时训练字典和线性分类器，获得了兼具重构性和判别性的字典。同样基于K-SVD算法，Jiang等人[10]提出了具有标签一致性的K-SVD算法（label consistent K-SVD，LC-KSVD），在训练字典的同时，添加了对训练信号具有判别性的稀疏编码误差项，此项约束使得属于同一类的信号具有十分相似的稀疏表示形式，从而突出了不同类别的差异性，故相比于D-SVD算法而言，LC-KSVD算法能进一步构建出更加优秀的字典。本文在LSC算法的基础上，通过引入LC-KSVD算法来改进原字典训练方法，以提高LSC算法的聚类精度，进而提出了聚类精度更好的改进算法ILSC（improved latent subspace clustering）。进一步地，虽然ILSC算法相对于LSC算法较好地提升了聚类精度，但在字典训练阶段的耗时也成倍增加。针对此缺陷，结合增量式字典训练的思想，提出了ILSC算法的增量式聚类算法I2LSC（incremental improved latent subspace clustering）。它在保证聚类精度的同时，进一步提高了运行速度。

本文组织结构如下：第2章介绍了基于稀疏表示的隐子空间聚类算法LSC；第3章介绍了LSC的改进型聚类算法ILSC；第4章介绍了ILSC的增量式聚类算法I2LSC；第5章为实验验证，采用聚类精度、归一化互信息（normalized mutual information，NMI）、芮氏指标（Rand index，RI）、运行时间等来评估算法性能；第6章总结全文。

2 相关知识

2.1 稀疏表示模型

稀疏表示提供了一种高维数据在低维子空间中表示的自然模型。模型假设信号y∈ℝK（即样本数据）可以表示为y≃Dx，其中字典矩阵D∈ℝK×M，稀疏表示向量x∈ℝM×N。即信号y可由字典D的原子（即字典D的列向量）线性表示，此时x的求取可以转换为如下问题的最优化：

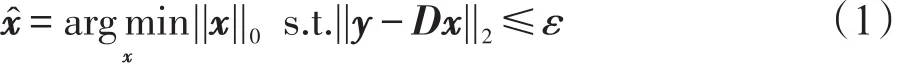
其中，ε为近似误差的阈值；ℓ0范数||c||0为稀疏表示向量x中的非零元素个数。最优化上式的问题是NP难的，但可以通过OMP算法[7]求得稀疏表示系数的近似解，如下式：

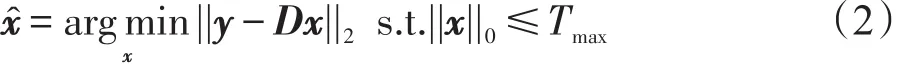
其中，Tmax为最大稀疏度。字典D可以预先设置或由信号y训练得到，具体参见文献[11]。例如，通过K-SVD算法[8]求解如下最优化问题可以得到字典D：

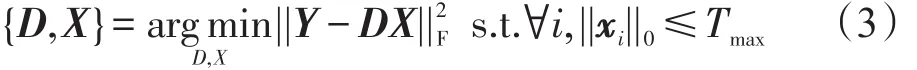
其中，Y∈ℝK×N是信号矩阵，其第i列为信号 yi；X∈ℝM×N是稀疏表示系数矩阵，其第i列为稀疏表示向量xi；Tmax是最大稀疏度。此时，每一个信号就可以由一些原子（即字典D的列向量）线性表示。

若使用ℓ1范数正则化代替ℓ0范数来加强稀疏性，x的求取就可以转换为如下问题的最优化：

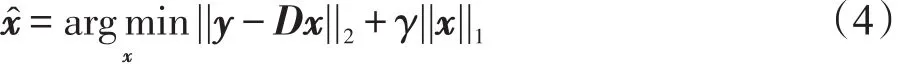
文献[12-13]中提供了多种针对ℓ1范数稀疏约束的最优化解法。

2.2 基于稀疏表示的隐子空间聚类算法

LSC算法是一种基于子空间聚类算法的改进算法，其利用系数矩阵提供的信号与原子间的关系信息来量化信号间潜在的联系。系数矩阵中非零系数的位置确定稀疏表示时所用的原子，系数的绝对值代表相应原子在稀疏表示时的权值大小。

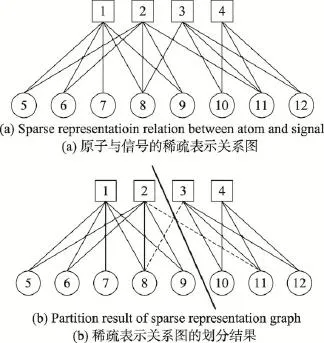
Fig.1 Sparse representation relation and partition result图1 稀疏表示关系及划分结果

图1（a）中，4个方形代表原子，8个圆形代表信号，原子与信号之间的连线表示信号在稀疏表示后与该原子的联系，可以根据这种潜在的联系对顶点集合进行划分。但在某些情况下，由于子空间的部分重叠，稀疏表示阶段的误差或噪声等原因，导致产生了不可分割的组，进而无法将集合完全地分割成不相交的子集。一种可行的办法是利用信号稀疏表示时最重要的一些原子作为特征来划分，相应的信号与原子间不重要的一些连线将被忽略（例如图1（b）中的虚线）。利用上述方法进行划分的结果如图1（b）所示，加粗的直线表示划分结果：第一组的顶点包括{1,2,5,6,7,8,9}，第二组的顶点包括{3,4,10,11,12}。

参照图1的方法，假定将样本信号Y={y1,y2,…, yN}看作其中的圆形，字典中的原子D={d1,d2,…,dM}看作其中的方形，在使用OMP算法求解信号Y的稀疏编码系数矩阵X时，一个信号yi可以由多个原子线性表示，则说明原子表示的圆形与信号表示的方形间存在一条连线，即相应信号与原子间有潜在联系。例如：图1（a）中的顶点6（即信号y6）与顶点1（即原子d1）和顶点2（即原子d2）间存在连线，则表示信号y6可以由原子d1、d2线性表示。信号与原子间的连线用集合E表示，此时两个不相交的顶点集合Y与D构成了无向图G=(Y,D,E)，为每条连线e∈E赋予一个权值wij，则非负邻接矩阵W={wij}的定义如下：

其中，Α=|X|（X为稀疏编码系数矩阵）。W的结构表明只有当原子与信号间存在稀疏表示关系时，才被赋予一个正数的权值，在原子与原子，信号与信号等其余情况中权值都为0。此时可以将信号Y的聚类问题转化为图G上的图划分问题，基于图论的最优划分准则是划分后使子图内部的相似度最大，子图之间的相似度最小。

本文使用规范割集准则（normalized-cut criterion）来划分图，其不仅能衡量同类别样本的相似度，同时考虑不同类别之间样本的差异性，并在寻求最优化分割的同时平衡每组样本的大小。文献[14]提供了一种求解规范割集准则问题的方法，此方法需要求解广义特征值问题：Lz=λDz。其中L=D-W是拉普拉斯矩阵，D是对角矩阵且，称为度矩阵，且拉普拉斯矩阵和度矩阵的定义如下：

其中，D1∈ℝM×M和 D2=ℝN×N是对角矩阵，表示第i个原子与所有信号相连边上的权值之和，表示第 j个信号与所有原子相连边上的权值之和。此时，等式Lz=λDz可以转化为如下形式：

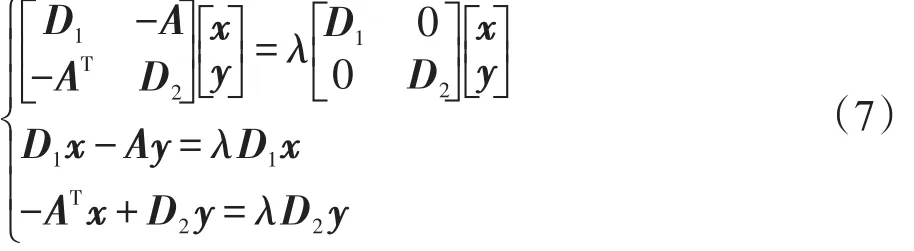
假设一个原子至少与一个信号相连（每个原子都至少在一次信号的稀疏表示中起作用），一个信号也至少与一个原子相连（每一个信号都至少由一个原子稀疏表示），故D1和D2都是非奇异的，将式（7）改写为：

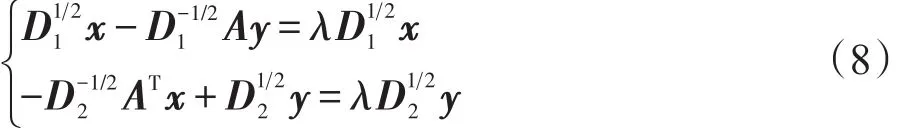
上式准确定义了矩阵An的奇异值分解（singular value decomposition，SVD）形式。其中μ和ν分别是相应的左右奇异向量，1-λ是相匹配的特征值。不同于传统谱聚类算法中计算相似度矩阵的第二小特征向量（即第二个最小特征值对应的特征向量），由于式（9）中特征值的形式为1-λ，故此时应计算矩阵An的第二大特征值对应的左右奇异向量 μ和ν，μ和ν分别包含图的最佳划分信息和原子的特征信息。此外与传统谱聚类算法相比，因为An是大小为M×N的矩阵，而传统谱聚类算法中的拉普拉斯相似度矩阵的大小为(M+N)×(M+N)，所以从计算时间的角度上讲，相似度矩阵An更有优势。

3 改进的隐子空间聚类算法ILSC

3.1 判别式字典训练算法

字典训练就是从数据中学习稀疏表示下的最优表示，同时训练初始字典使得字典中的原子特性更接近于所需表示的原始信号，以此获得性能优良并且规模更加紧凑的新字典。LSC算法中使用K-SVD算法构建字典，如式（3）所示，其目标函数只包含重构误差项，在构造字典的过程中具有一定的随机性，使得训练出的字典缺少足够的重构能力和判别能力。为了改进这一缺陷，本文利用训练信号中包含的类别信息，在式（3）的基础上添加了分类误差项，其中W是分类器参数，H= [h1h2…hN]∈ℝm×T是信号Y的类标签矩阵，m为类别数，hi=[0,0…1…0,0]T∈ℝm是对应于输入信号yi的标签向量，其中非零值的位置代表信号yi所属的类别。为了进一步增强字典的判别性，又添加了判别式稀疏编码误差项使系数矩阵X的形式接近于判别式稀疏编码矩阵Q，使得属于同一类别的信号具有十分相似的稀疏表示形式，并突出不同类别信号的差异性。综合考虑重构误差、判别能力以及线性分类性能这三方面因素提出如下的学习模型：

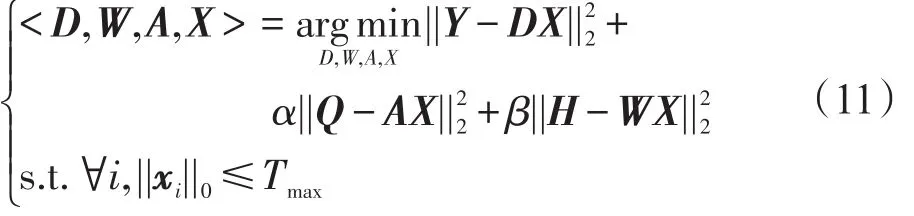
其中，α和 β是平衡因子；Q=[q1q2...qN]∈ℝK×T是关于信号Y的判别式稀疏编码矩阵；是对应于信号yi∈Y的判别式稀疏编码向量，如果信号yi和字典原子dk属于同一类，则向量qi中相应位置为1，否则为0。例如：假设有字典D=[d1d2…d6]和信号Y=[y1y2…y6]，其中y1、y2、d1、d2属于第一类，y3、y4、d3、d4属于第二类，y5、y6、d5、d6属于第三类，则矩阵Q定义如下：

每一列对应着一个信号的判别式稀疏编码。

A是一个线性变换矩阵，采用线性变换函数g(x;A)=Ax将原始稀疏表示系数x转换到更具判别性的稀疏特征空间RM中。为了计算方便，将式（11）改写为如下形式：

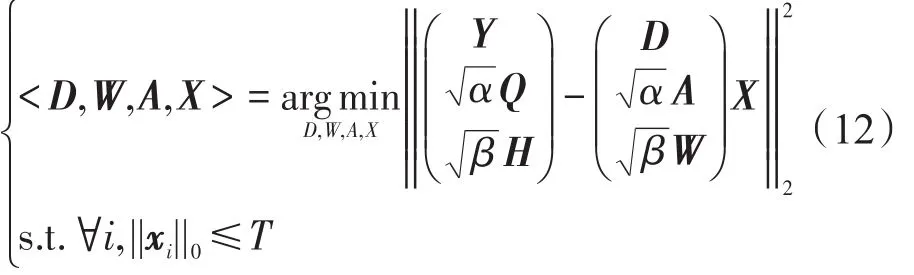
此时式（13）与式（3）的模型是相同的，因此可以用KSVD算法求得最优解，训练得到字典D。

3.2 初始化参数的推导

使用K-SVD算法求解字典学习模型式（13）时，需要具备初始化的字典Dnew，即需要对参数D、A、W进行初始化，具体方法如下。

对于字典D的初始化，针对每一类别的信号用K-SVD算法训练得到各自类别的字典，再将训练得到的字典合并为一个完整的初始字典D0，即所有类共享的字典。

对于参数A的初始化，使用多元岭回归正则化模型[15]来求解其初始值，相应的目标函数如下：

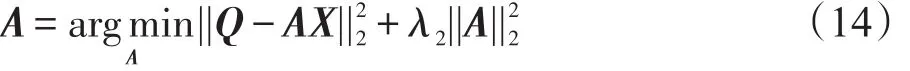
其解为：

参数W的初始化与参数A类似，利用上述模型求得如下的解：

其中，参数X是在已知初始字典D0的情况下，使用K-SVD算法所求得的信号Y的稀疏表示系数矩阵。

3.3 ILSC算法的步骤

输入：Y,m。

输出：测试信号Y2的聚类标签。

步骤1将信号Y分为Y1∈ℝK×T和Y2∈ℝK×N两部分，Y1为训练信号，带有标签信息，用于训练字典，Y2为测试信号，不带标签信息，用于测试聚类算法，即Y1∈Y,Y2∈Y,Y1⋃Y2=Y。

步骤2求得训练信号Y1的判别式稀疏编码矩阵Q∈ℝM×T和类标矩阵H∈ℝm×T（参照2.1节）。

步骤3使用K-SVD算法求解式（13）得到字典D，其中Dnew的初始化参照3.2节。

步骤4使用OMP算法，利用字典D构建测试信号Y2的稀疏表示矩阵C∈ℝM×N，使得Y≃DC。

步骤5构建矩阵A=|C|，计算度矩阵D1和D2，求得矩阵（参照2.2节）。

步骤6使用奇异值分解算法计算矩阵An的前ℓ=[lbm]个左右奇异向量 μ2,μ3,…,μℓ+1和ν2,ν3,…, νℓ+1。

步骤7构建矩阵，其中U=[μ2,μ3,…,μℓ+1]，V=[ν2,ν3,…,νℓ+1]。

步骤8对ℓ维数据集Ζ进行k-means聚类，聚类标签的最后N行是测试信号Y2的聚类结果。

在ILSC算法中，字典训练阶段需要使用部分信号的标签信息，因此与LSC算法不同，ILSC算法需要从原始信号中抽取一部分带标签的信号用于训练字典，而LSC算法则是用所有的信号去随机地训练一个字典。此外在字典训练阶段，ILSC算法和LSC算法虽然都是使用K-SVD算法求解字典，但Dnew相比于LSC中的D包含更多的判别信息，因此在ILSC算法中可以训练出更具判别性的优秀字典。与此同时，由于Dnew规模的增大，也使得字典训练的耗时大幅增加。

4 ILSC算法的增量式聚类算法I2LSC

4.1 增量式字典训练算法

在ILSC聚类算法中，使用LC-KSVD算法训练字典，相比于原先的K-SVD算法，可以训练得到判别性更好的字典，因此提高了算法的聚类精度。但是字典训练阶段的耗时也随之大幅增加，为了改进这一问题，引入增量式字典训练的思想来求解字典。为了保证训练所得的字典具有足够的判别性，同样采用式（11）的学习模型，通过最优化如下ℓ1范数约束的目标函数求解字典D：

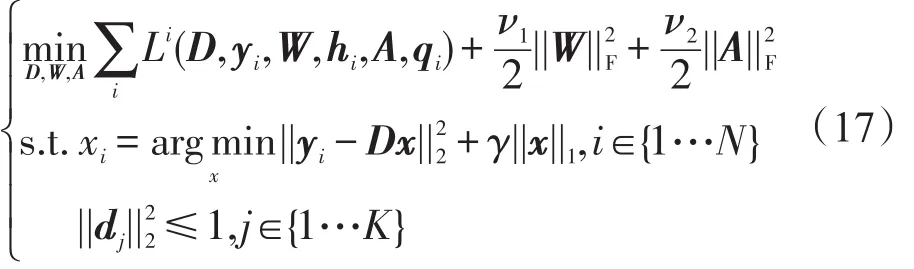
首先采用链式规则计算Li关于字典D的梯度得：

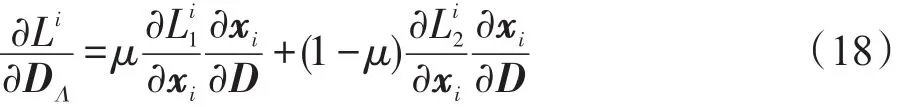
接着，参考文献[16-18]，利用不动点方程的隐函数微分来构建式（4）的不动点方程 DT(Dx-y)= -γsign(x)，并计算方程关于字典D的梯度得：

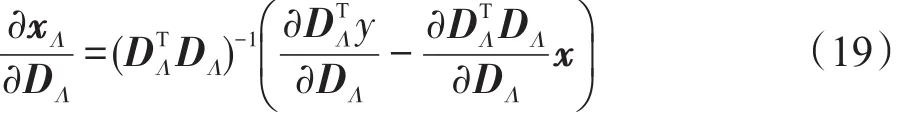
其中，Λ表示稀疏编码系数xi中非零值的索引集合；表示系数中零值的索引集合。

最后求解Li关于D、A、W的梯度，定义辅助变量ϕμ,μ∈{1,2}，使得，其中。此时可以求得故Li关于字典D的梯度如下：

此外，对Li直接求解关于A和W的梯度，其结果如下：

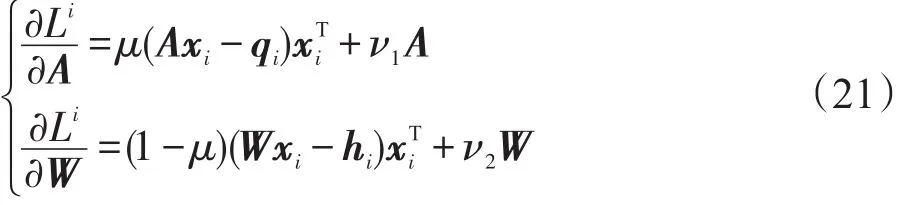
4.2 I2LSC算法的步骤

输入：Y,m,D1,A1,W1,ρ,n,M,μ,ν1,ν2,b。

输出：测试信号Y2的聚类标签。

步骤1将信号Y分为Y1∈ℝK×T和Y2∈ℝK×N两部分，Y1为带有标签信息的训练信号，用于训练字典，Y2为不带标签信息的测试信号，用于聚类算法，即Y1∈Y,Y2∈Y,Y1⋃Y2=Y。

步骤2求得训练信号Y1的判别式稀疏编码矩阵Q∈ℝM×T和类标矩阵H∈ℝm×T（参照2.1节）。

步骤3增量式训练字典D（参照3.1节）：

for i=1…n

（1）依次从信号Y1中随机抽取一批信号，计算其对应的qi∈Q和hi∈H；

for j=1…T/b

（2）根据式（4）计算y(i)的稀疏表示xi

（3）根据xi中非零值的位置，得到索引集合Λi，并计算辅助变量ϕ1和ϕ2

（4）选择学习率ρi=min(ρ,ρi0/i)

（5）通过式（20）、（21）更新参数D、A、W

D、A、W的初始化参照3.2节

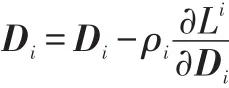
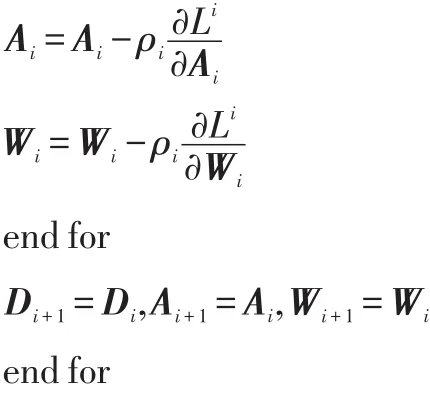
步骤4其余步骤与ILSC算法相同。

在I2LSC算法中，使用与ILSC类似的字典训练模型，但求解最优化的方式不同，I2LSC中使用增量式算法每次读取一小批信号来训练字典，并用梯度下降算法更新最优参数。梯度下降算法拥有较快的寻优速度，因此I2LSC中的增量式字典训练算法在保证字典判别性的同时，减少了字典训练的耗时。

5 实验结果与分析

实验平台：Intel®CoreTMi3-3240 CPU；主频：3.40 GHz；内存：4 GB；系统类型：Win7 64位操作系统；编程环境：Matlab R2014a（8.3.0.532）。

为了对本文算法的性能进行有效评价，本文选取如下4种指标：

（1）聚类精度（clustering accuracy assessment）[6]

（2）归一化互信息（NMI）[19-20]

（3）芮氏指标（RI）[19-21]

（4）算法耗时

聚类精度是类别被正确标记的信号占总信号数的百分比；NMI、RI两种指标，其取值范围均为[0,1]，值越靠近1说明聚类效果越好，反之值越靠近0说明聚类效果越差。

5.1 实验数据

本文采用ExtendedYale B(B+)、Scene-15、Caltech-101、手写数字数据集MNIST等4个数据集验证本文算法的有效性。

Extended Yale B[22]人脸库是一个包含28个人在9种不同姿态和64种不同光照条件下共16 128张人脸图片的数据库，为了实验的可操作性，将每张图像的尺寸都调整为48×42像素大小，构成一列信号yi∈ℝ2016。因为对数据归一化后可以加快梯度下降求最优解的速度，且可能提高精度，所以用式（22）对信号yi做归一化处理。

Caltech101[23]图像数据集包含花、车辆、动物等101个类别共计9 146幅图像。每类包含的图像数目从31～800不等，图像尺寸约为300×300像素。实验中，将图像库中的图片都转化为灰度图，采用稠密SIFT（scale-invariant feature transform）[24]特征提取算法进行图像局部特征描述，提取SIFT特征的图像块大小为16×16像素，步长为6像素。同时基于提取的SIFT特征利用空间金字塔匹配（spatial pyramid matching，SPM）特征对其进行提取，金字塔总层数为3层，大小分别为1×1、2×2、4×4。最后采用k-means算法对空间金字塔进行聚类得到视觉编码表，并用PCA（principal component analysis）算法将维度降至3 000维。

Scene-15[24]图像数据集包含卧室、厨房、城市场景等15个类别共计4 485幅自然场景图。每类包含的图像数目从200～400不等，图像尺寸约为250×300像素。实验中，利用一个四层金字塔的SIFT描述子编码本计算空间金字塔特征，并用PCA算法将维度降至3 000维。

MNIST手写数字数据集包含10类共计70 000个手写数字的图像样本，样本维数为784。同样对MNIST数据集用式（22）做归一化处理。

5.2 实验设置

为了验证本文算法的有效性，对SSC算法、LRR算法、LSC算法、ILSC算法及I2LSC算法在聚类精度、NMI值、RI值三方面的表现进行比较。同时为了进一步说明I2LSC算法相较于ILSC算法在运行时间上的优势，对比LSC、ILSC、I2LSC算法完整的运行时间，这3种算法在聚类阶段的步骤完全一致，同时也对3种算法在字典学习阶段的耗时进行比较。

在聚类精度、NMI值、RI值的对比实验中，对数据集Extended Yale B和Scene-15，为了保证实验的随机性，实验中随机选取m=2…8类，即m个尺度划分，每个类别选取T=60个信号构成包含T×m列的训练数据集，用于字典训练，剩余的信号构成测试数据集，用于测试聚类精度、NMI、RI值。对数据集Caltech101，由于其每类包含的信号数从31～800不等，为了保证足够的信号数，需要从信号数足够的类别中抽取信号，其余同上。参考文献[6]，当测试信号数与字典大小的比率N/M＞10时，LSC聚类算法可以获得较好的聚类效果，故字典的大小M设置如表1所示。

Table 1 Dictionary sizeMcorresponding to different scales m表1 不同划分尺度m对应的字典大小M

在增量式字典训练中，学习率ρ取0.01，迭代次数n取20，平衡系数 μ取0.6，ν1、ν2取10-6。增量式字典训练算法的步骤3中，每批数据块的大小为总训练信号数的10%，即b=T×10%。平衡因子的取值也可以由用户根据实际样本进行调整，但必须在经验值范围内取值。计算以上5种算法在各个数据集上的聚类精度、NMI和RI的均值以及标准差，其中均值反映了算法的平均聚类性能，标准差反映了算法的稳定鲁棒性。

在算法耗时的对比实验中，对Extended Yale B、 Caltech101、Scene15数据集，划分尺度m取8，每个划分尺度中训练信号的个数T取100。对MNIST数据集，m取6，T取5 000。其余同上。最后统计3种聚类算法的整体耗时情况和聚类算法在字典训练阶段的耗时。以上所有实验均重复40次，并且每次随机选取不同的样本集合。

5.3 实验结果

各算法在3个数据集Extended Yale B、Scene-15、Caltech101上的聚类精度、NMI、RI值如表2～表10所示。其中最优均值都已用黑体标出。对比各表的实验结果可以发现，随着划分尺度的增大，即类别m的增大，5种聚类算法SSC、LRR、LSC、ILSC、I2LSC的聚类精度、NMI、RI值在大多数情况下都逐渐下降，并且以SSC、LRR、LSC算法下降幅度最大，而ILSC和I2LSC算法的下降速度都较慢。这是因为判别式字典的训练过程中使用到训练信号的标签信息，当类别数增加时，相应类别的标签信息也会被添加进字典训练阶段。因此，在类别数增大时，相比于SSC、LRR、LSC算法，ILSC和I2LSC算法具有更稳定的聚类精度、NMI、RI值。此外，在所有聚类精度、NMI、RI值的对比实验中，ILSC和I2LSC算法的聚类精度、NMI、RI值均远优于LSC算法，在某些情况下具备良好的鲁棒性，且在大多数情况下，I2LSC算法的聚类精度、NMI、RI值均优于ILSC算法。以上说明也验证了由于在字典训练阶段合理使用了部分标签信息，使得训练得到的字典更具判别性，进而使信号稀疏表示的结果更加准确，最终提升了算法的聚类精度、NMI、RI值。

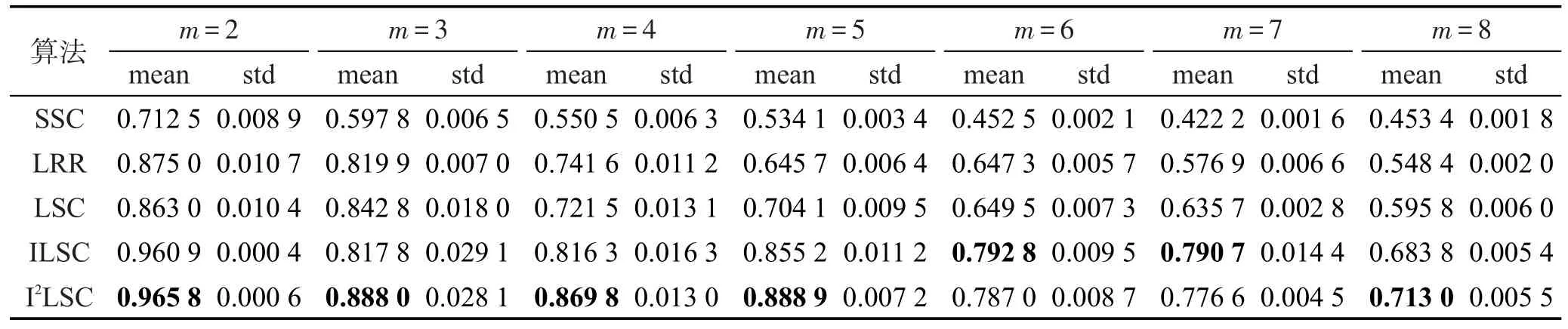
Table 2 Clustering accuracy assessment of 5 clustering algorithms on Extended Yale B dataset表2 5种聚类算法在Extended Yale B数据集上的聚类精度

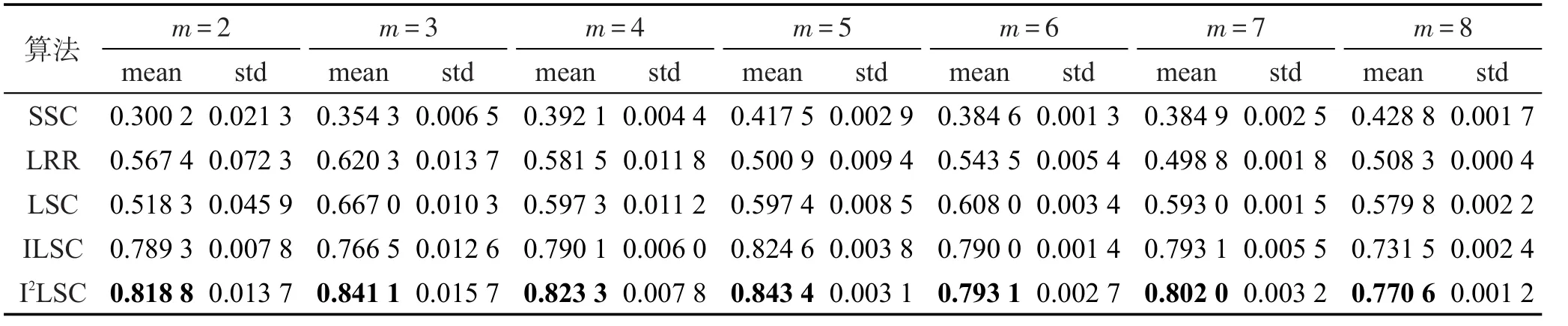
Table 3 NMI of 5 clustering algorithms on Extended Yale B dataset表3 5种聚类算法在Extended Yale B数据集上的NMI值

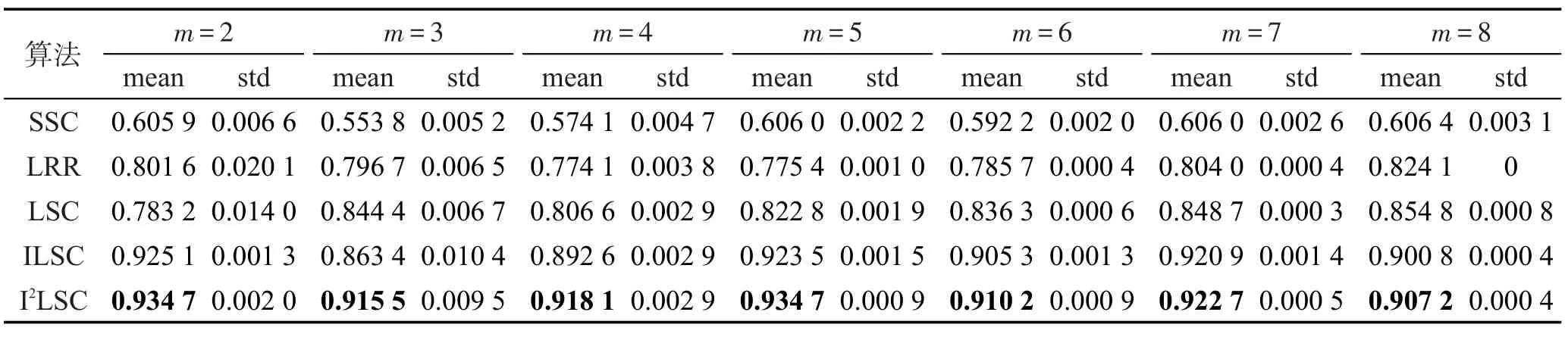
Table 4 RI of 5 clustering algorithms on Extended Yale B dataset表4 5种聚类算法在Extended Yale B数据集上的RI值

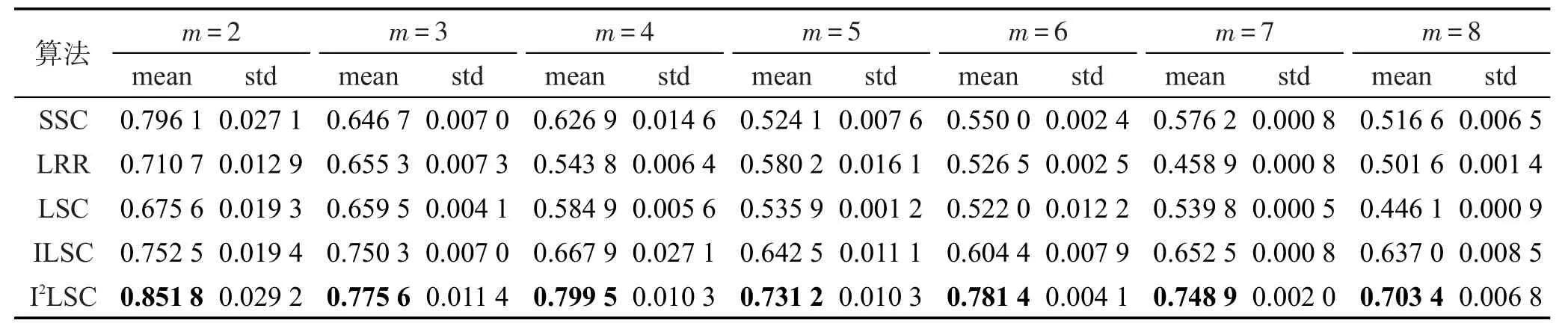
Table 5 Clustering accuracy assessment of 5 clustering algorithms on Caltech101 dataset表5 5种聚类算法在Caltech101数据集上的聚类精度

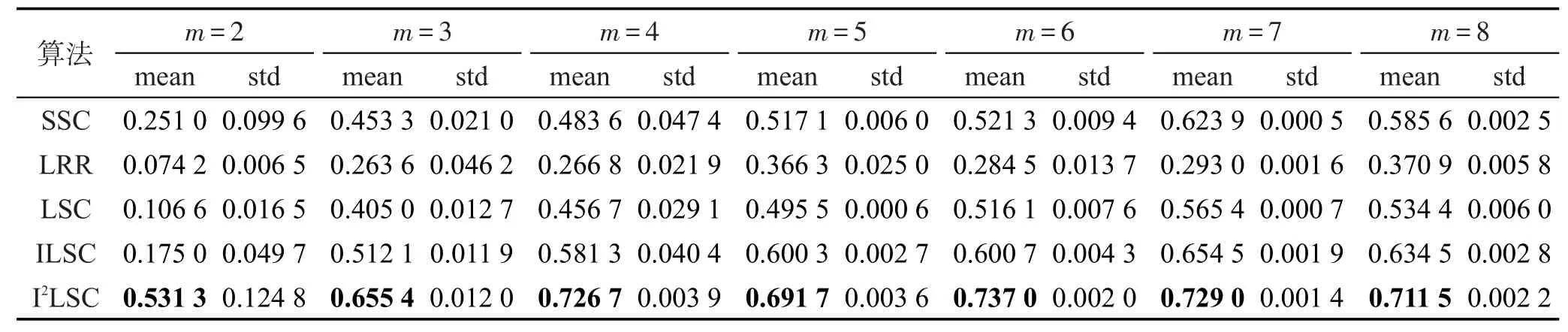
Table 6 NMI of 5 clustering algorithms on Caltech101 dataset表6 5种聚类算法在Caltech101数据集上的NMI值

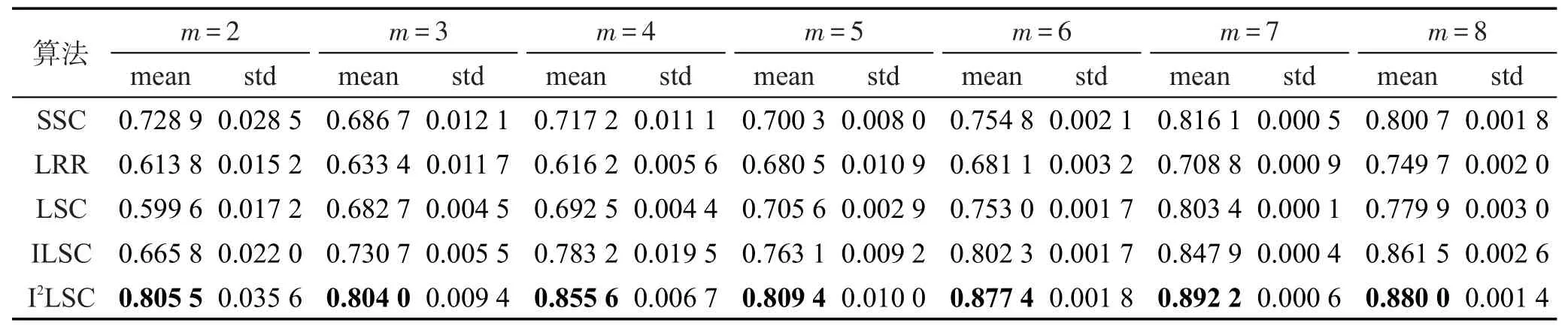
Table 7 RI of 5 clustering algorithms on Caltech101 dataset表7 5种聚类算法在Caltech101数据集上的RI值

在不同数据集上，LSC、ILSC、I2LSC聚类算法的整体耗时及算法在字典训练阶段的耗时情况如表11和表12所示。

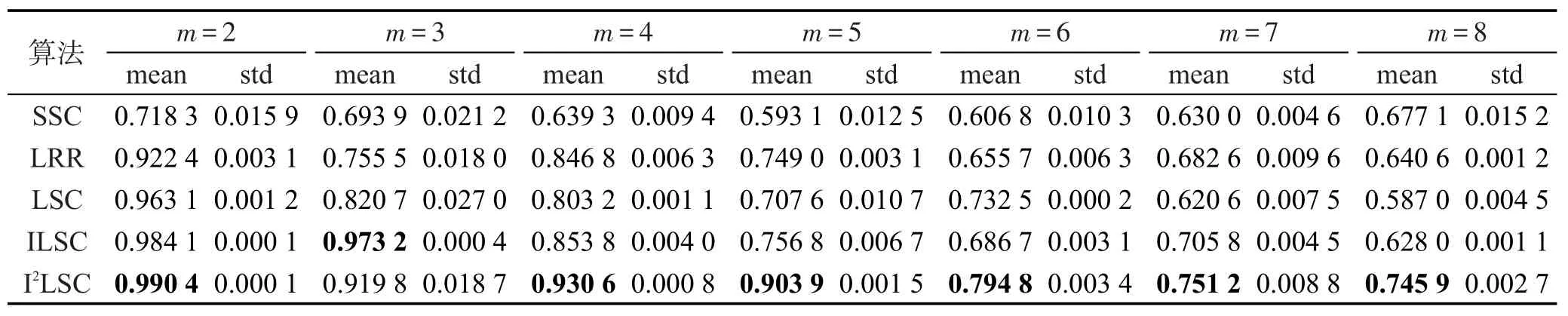
Table 8 Clustering accuracy assessment of 5 clustering algorithms on Scene-15 dataset表8 5种聚类算法在Scene-15数据集上的聚类精度

Table 9 NMI of 5 clustering algorithms on Scene-15 dataset表9 5种聚类算法在Scene-15数据集上的NMI值

Table 10 RI of 5 clustering algorithms on Scene-15 dataset表10 5种聚类算法在Scene-15数据集上的RI值

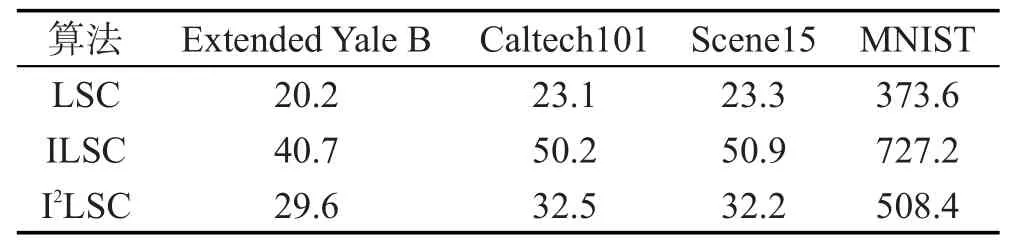
Table 11 Elapse of 3 algorithms in dictionary training phase表11 3种算法在字典训练阶段的耗时 s

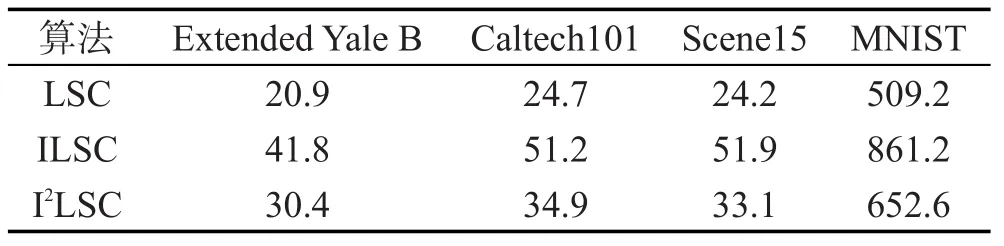
Table 12 Elapse of 3 algorithms in entire clustering phase表12 3种算法完整的耗时 s

对比3种聚类算法LSC、ILSC、I2LSC在不同数据集上训练字典所需的时间，参照表11可以看出LSC算法最快，ILSC算法最慢。这是因为LSC和ILSC算法最优化求解字典的方式类似。但由于ILSC算法在求解字典的过程中除了原有的重构误差项外，还添加了分类误差项和稀疏编码误差项，使得初始字典Dnew的规模远大于LSC算法中的初始字典D，致使最优化时的耗时大幅增加。此外，I2LSC算法在字典训练阶段的耗时远低于ILSC算法，只比LSC算法的耗时多一点，这也验证了之前的猜测，同等规模下使用梯度下降方式最优化的速度远快于使用K-SVD算法进行最优化。同时，对比表5和表6可以看出，在Extended Yale B、Caltech101、Scene15这些小样本数据集上，字典训练阶段的耗时基本等同于聚类算法的完整耗时；在MNIST这样的大样本数据集上，字典训练阶段的耗时也占聚类算法完整耗时的80%左右。因此，减少字典训练阶段的耗时对提高聚类算法的整体运行效率有显著效果。

综合以上所有实验可以看出，ILSC算法相比于LSC算法拥有更优的聚类精度，更进一步，I2LSC算法在拥有优秀聚类精度的前提下还能保证较快的运行速度。

6 结束语

基于稀疏表示的隐子空间聚类算法LSC由于字典训练算法过于简单，导致训练得到的字典缺少足够的表示能力和判别能力，影响到数据的稀疏表示，进而降低了算法的聚类精度。针对以上问题，本文改进其字典训练方法，利用已有的样本类别信息，从多尺度字典中训练得到具有优秀重构性和判别性的过完备字典，提出了ILSC算法。此外，为了提高字典训练算法的效率，改进了字典训练模型的最优化过程，提出了增量式判别字典训练算法，使得ILSC算法的增量式算法I2LSC在拥有优秀聚类精度的同时，具有较好的运行速度。

目前，ILSC和I2LSC算法仍存在一些不足，以上实验中字典的大小是根据经验设定的，一般来说字典中原子数目越多其包含的信息也越多，对聚类精度的影响也越大，但字典过大会导致冗余，并且会大幅增加字典训练阶段的耗时。另外，在验证增量式字典训练算法的实验中，每批数据块大小被设定为10%，数据块的大小对每次训练样本包含的特征信息量以及算法的迭代次数都有影响，最终将影响算法的运行时间和训练所得字典的判别性。因此，如何科学有效地设定字典大小和数据块大小将是下一步的研究方向。

[1]Vidal R.Subspace clustering[J].IEEE Signal Processing Magazine,2011,28(2):52-68.

[2]Elhamifar E,Vidal R.Sparse subspace clustering[C]//Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition,Miami,USA,Jun 20-25,2009. Piscataway,USA:IEEE,2009:2790-2797.

[3]Liu Guangcan,Lin Zhouchen,Yu Yong.Robust subspace segmentation by low-rank representation[C]//Proceedings of the 27th International Conference on Machine Learning, Haifa,Israel,Jun 21-24,2010.Red Hook,USA:Curran Associates,2014:663-670.

[4]Favaro P,Vidal R,Ravichandran A.A closed form solution to robust subspace estimation and clustering[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition,Colorado Springs,USA,Jun 20-25,2011. Washington:IEEE Computer Society,2011:1801-1807.

[5]Shi J,Malik J.Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.

[6]Adler A,Elad M,Hel-Or Y.Fast subspace clustering via sparse representations[R].Department of Computer Science, Technion,Tech,2011.

[7]Pati Y C,Rezaiifar R,Krishnaprasad P S.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the 27th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,USA,Nov 1-3,1993.Piscataway,USA:IEEE, 1993:40-44.

[8]Aharon M,Elad M,Bruckstein A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54 (11):4311-4322.

[9]Zhang Qiang,Li Baoxin.Discriminative K-SVD for dictionary learning in face recognition[C]//Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition,San Francisco,USA,Jun 13-18,2010.Piscataway,USA:IEEE,2010:2691-2698.

[10]Jiang Zhuolin,Lin Zhe,Davis L S.Learning a discriminative dictionary for sparse coding via label consistent K-SVD [C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition,Colorado Springs,USA, Jun 20-25,2011.Washington:IEEE Computer Society,2011: 1697-1704.

[11]Rubinstein R,Bruckstein A M,Elad M.Dictionaries for sparse representation modeling[J].Proceedings of the IEEE,2010,98(6):1045-1057.

[12]Lee H,Battle A,Raina R,et al.Efficient sparse coding algorithms[C]//Proceedings of the 20th Annual Conference on Neural Information Processing Systems,Vancouver,Canada, Dec 4-7,2006.Red Hook,USA:Curran Associates,2012: 801-808.

[13]Gregor K,Lecun Y.Learning fast approximations of sparse coding[C]//Proceedings of the 27th International Conference on Machine Learning,Haifa,Israel,Jun 21-24,2010. Red Hook,USA:CurranAssociates,2014:399-406.

[14]Dhillon I S.Co-clustering documents and words using bipartite spectral graph partitioning[C]//Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Francisco,USA, Aug 26-29,2001.New York:ACM,2001:269-274.

[15]Golub G H,Hansen P C,O'Leary D P.Tikhonov regularization and total least squares[J].SIAM Journal on Matrix Analysis andApplications,1999,21(1):185-194.

[16]Bagnell J A,Bradley D M.Differentiable sparse coding[C]// Proceedings of the 22nd Annual Conference on Neural Information Processing Systems,Vancouver,Canada,Dec 8-10,2008.Red Hook,USA:CurranAssociates,2009:113-120.

[17]Mairal J,Bach F,Ponce J.Task-driven dictionary learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(4):791-804.

[18]Yang Jianchao,Yu Kai,Huang T.Supervised translation invariant sparse coding[C]//Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco,USA,Jun 13-18,2010.Piscataway,USA: IEEE,2010:3517-3524.

[19]Liu Jun,Mohammed J,Carter J,et al.Distance-based clustering of CGH data[J].Bioinformatics,2006,22(16):1971-1978.

[20]Deng Zhaohong,Choi K S,Chung F L,et al.Enhanced soft subspace clustering integrating within-cluster and betweencluster information[J].Pattern Recognition,2010,43(3): 767-781.

[21]Rand W M.Objective criteria for the evaluation of clustering methods[J].Journal of the American Statistical Association, 1971,66(336):846-850.

[22]Georghiades A S,Belhumeur P N,Kriegman D J.From few to many:illumination cone models for face recognition under variable lighting and pose[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(6):643-660.

[23]Li Feifei,Fergus R,Perona P.Learning generative visual models from few training examples:an incremental Bayesian approach tested on 101 object categories[J].Computer Vision and Image Understanding,2007,106(1):59-70.

[24]Lazebnik S,Schmid C,Ponce J.Beyond bags of features: spatial pyramid matching for recognizing natural scene categories[C]//Proceedings of the 2006 IEEE Conference on Computer Vision and Pattern Recognition,New York,Jun 17-22,2006.Washington:IEEE Computer Society,2006: 2169-2178.

DONG Qi was born in 1990.He is an M.S.candidate at School of Digital Media,Jiangnan University.His research interests include artificial intelligence,pattern recognition,dictionary learning and subspace clustering algorithm.

董琪（1990—），男，江南大学数字媒体学院硕士研究生，主要研究领域为人工智能，模式识别，字典学习，子空间聚类算法。

WANG Shitong was born in 1964.He is a professor at School of Digital Media,Jiangnan University.His research interests include artificial intelligence,pattern recognition and bioinformatics.

王士同（1964—），男，江南大学数字媒体学院教授，主要研究领域为人工智能，模式识别，生物信息。

Improved Latent Subspace ClusteringAlgorithm and Its Incremental Version*

DONG Qi+,WANG Shitong
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China

+Corresponding author:E-mail:dq_nyr@163.com

DONG Qi,WANG Shitong.Improved latent subspace clustering algorithm and its incremental version.Journal of Frontiers of Computer Science and Technology,2017,11(5)：802-813.

Compared with the traditional subspace clustering algorithms,the latent subspace clustering(LSC)algorithm based on sparse representation has faster clustering speed,thereby it can be applied into larger data sets.However it still has two shortcomings.One is the randomness and slowness in dictionary training phase and the other is its occupying too much memory.On the basis of the LC-KSVD algorithm,this paper proposes the ILSC(improved LSC)algorithm to obtain its enhanced clustering accuracy by adding some labels into the dictionary training phase to improve its discrimination.However,compared with the LSC algorithm,ILSC algorithm consumes more time in dictionary training phase.In order to circumvent this drawback,based on the idea of incremental training,this paper develops the I2LSC(incremental ILSC)algorithm to achieve comparable clustering performance to ILSC algorithm in the sense of clustering accuracy,NMI(normalized mutual information)and RI(Rand index),but faster speed than ILSC.

subspace clustering;latent subspace clustering(LSC);discriminant dictionary training;incremental dictionary training

10.3778/j.issn.1673-9418.1601005

A

TP391

*The National Natural Science Foundation of China under Grant No.61170122(国家自然科学基金);the New Century Excellent Talent Foundation from MOE of China under Grant No.NCET-12-0882(教育部新世纪优秀人才支持计划).

Received 2016-01,Accepted 2016-03.

CNKI网络优先出版:2016-03-07,http://www.cnki.net/kcms/detail/11.5602.TP.20160307.1710.018.html