基于分布式技术的多级数据真值发现∗
基于分布式技术的多级数据真值发现∗
吕维新殷军
(云南电网有限责任公司昆明供电局昆明650200)
为了进一步提升数据管理系统的可靠性和准确性,论文提出了一种基于分布式技术的多级数据真值挖掘发现,消除了级别之间的差异性与独立性。该方法将数据源的数据相值进行分级,利用级值与真实值相似度定义准确率迭代,避免了同一数据在不同级被抽取时的差异性。通过在分布式技术挖掘算法下,分别计算级值概率和偏离度来判断多级数据真实值。最后,通过对重叠数据集的实验说明了论文提出的多级数据真值发现的高效性。
多级数据;真值发现;分布式;数据挖掘
Class NumberTN919.3
1 引言
随着互联网计算机的兴起,人们越来越依赖于大数据带来的信息与资源,对于信息的可靠性与准确性提出了更高的要求[1~2]。多级数据在来源上具有复杂性与模糊性,已有的真值算法采用迭代机制来进行真值发现[3]。数据源质量越高,提供的值正确率也越高,与真实值的偏差也越小。来源提供的值与真实值的偏差越小,值质量越高,来源质量也越高,数据源质量和值质量二者相互依赖[4~5]。本研究也采用分布式真值发现迭代算法,用提供值的所有来源准确率衡量值可靠性,选出真实值,用来源提供的所有值与“真实值”的相似度衡量来源可靠性,在迭代过程中一步一步地逼近真实值。
2 多级数据理论
2.1符号说明
为了方便描述多级数据问题,给相关概念及其符号给出详细解释[6],如表1所示。
根据表1对多级数据的定义,s→f表明由来源s提供事实f。f→i表明由事实f来对数据项I进行描述。fi表示事实f的第i级数据集的值,fi→f表示级值fi是事实f的一部分。tf表明由事实f进行描述的数据项的真值,tfi表明由事实f进行描述的数据项的真值在第i级上的体现。一般来说,每一个数据项真值情况有所不同,有的数据项存在多个真值,而有的数据项仅存在单真值,本文将仅对单真值的数据项进行考察。

表1 符号说明
2.2理论分析
对于每一组数据的来源,其在不同的数据项上提供事实,但存在对于不同的数据项覆盖率不同的情况,一些数据来源能够提供相当数量的数据项值,而有些数据来源仅能提供少量的数据项值[7]。这和数据来源的质量也有很大的关系。同一个数据来源其自身提供的值可能存在一定的冲突[8],为了找出真实值,我们需要解决这样的自冲突。因此,本文研究的问题可简述如下:1)给定一定集合数据的数据源并提供其事实数据[9];2)研究如何为不同的数据项筛选出其真实值[10]。基于分布式技术挖掘算法下,本文将给出以下假设来简化所研究的问题,如下所示。
1)假设每个数据项仅存在单真值。当同一个数据项存在多个事件发生冲突时,必定能找到唯一的真值。
2)数据来源提供的数据相互独立,对于不同数据源之间存在的联系情况并不在考虑的范围之内。
3)每个数据项之间是相互独立的,对于不同的数据项的事实,其为真的概率相互之间没有关联。
4)数据项的级别之间互不干扰相互独立,不同级值为真的概率相互之间没有关联。
分布式技术挖掘算法是基于迭代的思想而实现的[11]。在上述的四个假设之下,每一循环的迭代过程主要包含下述两个主要的关键步骤:
1)针对每一个数据项的值进行分级,并对每件事实f进行拆分,将其划分为多条级值{f1,f2,…,fL(f)},根据数据项所提供的fi(1≤i≤L(f))的来源的配适率得出各个级值fi获得的投票,同时以各条级值fi获得的投票为依据来获得完整的关于事实f的投票,再筛选出得到投票数最高的数据项的值作为“真实值”。
2)演绎出事实f的级值fi(1≤i≤L(f))以及其与“真值”对应的级值tfi的相似程度,并以每级的相似度为依据来计算出完整事件事实f以及“真值”tf的相似程度,并根据所选数据来源的配适率来对下一轮的数据处理进行迭代。
3 分布式真值发现
3.1级值计算
本文借鉴贝叶斯公式计算fi,即P(fitrue|ψ(fi)),其中fi为计算概率为真的公式,并从中筛选出表示fi概率为真的投票值大小的算法并得出fi所获得的投票[5]。根据上述的假设3),事实fi为真的概率仅仅与f所描述的提供真值的数据项来源相关。再根据上述的假设4),fi为真的概率仅仅与f所描述的数据项第i级值分布相关。|S(fi)|表示提供特定极值i的事实f来源的数量,其中绝对值表明该数据集合的大小。|S∧(fi)|表示提供特定极值i的事实f来源的数量,即提供错误极值的来源数量。利用|S∨(fi)|表示|S(fi)|∪|S∧(fi)|的集合,数据项来源的配适率由A(s)表示。某个数据项来源错误的概率在本文中用Pop(f)表示,简写为P(fi),完整值的投票数由C(fi)表示,通过推算得到下式:

本文利用上式来计算提供不同质量的数据来源的不同极值i的事实fi的总投票数,其总的投票数量越高,fi为真的概率则越高。
3.2完整值计算
本文将采取按照级别的高低乘以权重再叠加的方法来计算出完整值的投票数。数据项分级越高则在决定完整值的投票数时其地位越发重要也越有话语权,规定级别从1开始,随着数值的增大其代表的级别也越高[12]。当数据项的数值与地理信息位置相联系的时候,其级别数越高,与其对应的地理位置的范围就越广,同样,当数据项的数值与长度、重量、距离等相联系的时候,其级别越高,相对应的等级也就越大。当一个数据项的数值为数字时,其级别越大越具有发言权,也就是数值的大小最大程度地取决于其数量等级较高的数字,在信息位置上此原理同等适用,级别越高的数值决定基本的位置的范围。这样的原理运用到完整值的投票数之上,则其等级越高,权重越大。
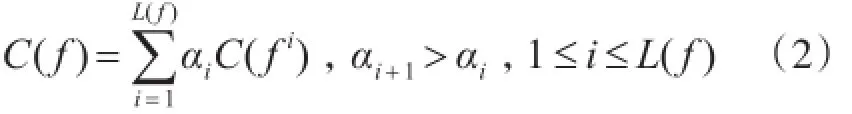
根据每个级值获得的投票数和相对应的影响因子相乘并进行累加,可计算出完整值的投票数。假定数据项级别i的权重为1,各个级别之间的权重比均为α,同时设α>1,可得到如下表达式:
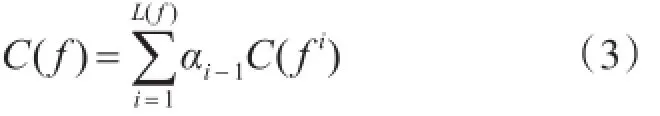
根据上式,依据所选范围内的所有数据项的事实f完整值投票数筛选出每一个数据项的“真值”。依据表1中的假设1),同一个数据项存在多个事件发生冲突时,必定能找到唯一的真值。因此可根据数据项上投票数目最多的原则选择对应的事实f作为真值。
3.3真值计算
评判数据来源提供数据质量的标准是,数据来源所提供的值同“真值”之间的相似程度,两者之间的相似程度越高则数据来源提供值的质量则越高,也就是说当数据来源所提供的值同“真值”之间的相似程度较低时,数据来源提供值的质量则越低。本文利用来源所提供的值同“真值”之间的相似程度来表示来源提供值的质量[13]。当数据项中来源提供值的质量越高,则其配适率越高。数据来源在它所提供了值的所有的数据项上的综合表现会影响到来源配适率的评价。为了防止极端的数据项值两极分化带来的数据波动从而影响到数据配适率的计算,本文将来源所提供的值同“真值”之间的相似程度的平均值作为来源的配适率,如式(3)所示。在计算过程中将来源所提供的值同“真值”之间的相似程度的演算过程划分为两个步骤:1)计算出来源所提供的值同“真值”之间的相似程度;2)按照级别的高低乘以权重再叠加计算出完整值同真值之间的相似程度。假设相邻的两个级别之间的影响因子之比均为β,同时假定β>1,所有的权重系数之和为1,由此可得:

3.4算法描述
input:对于来自每个数据源的事实的集合F划分为若干个数据源S。
output:真值集合与数据源的质量指标。
Letα=2.5,β=1.5,A(s)=0.6根据(1)式计算βl
for eachs∈S//初始化数据源质量
end
repeat
for eachi=I//根据(16)式计算βl
for eachf,f→i//根据(7)、(8)式计算第i个数据项事实的投票数
for eachfi→f//根据(9)式计算事实的投票数
end//选出数据项i的真实值
end
end
for eachs∈S//计算第i个数据项事实级值与对应级数真实值之间的相似度
for eachf,s∈f//根据(15)式计算完整值f与对应真实值之间的相似度
for eachfi,fi∈f//根据(13)式计算数据来源s的准确率A(s)
end
end
end
until Convergence//计算直到真实值收敛于级值
returnP(f)andA(s)
4 实验分析
4.1实验准备
本文以Java语言为工具对本文算法同之前常用算法进行对比。JDK的版本为JDK6.0。实验所选取的处理器为Intel Core i7-2600,实验过程在内存为16GB的Thinkpad笔记本上进行,操作系统为Windows10。
4.2性能评价
本文采取配适率的指标来对算法进行评价。利用数据集来提供“真值”由此组成“真值”集合,由于数据集较为庞大,提供的数据项值数量众多,如若全部采用人工验证的方法其代价太大,因此仅包含少数部分的数据项。本文将算法输出的真实值同真值的集合的数值比较以此来对算法的结果进行评价。集合A表示分布式数据真值发现输出的同数据项所对应的“真实值”,集合B表示集合A描述的数据项的子集,它表示真实值集合所描述的数据项。算法准确率的计算公式为

本文所采取的分布式真值发现在对其输出配适率计算时数据来源所提供的值同“真值”之间的相似程度进行衡量。依据不同的数据集的性质采取不同的数据采集方法和相似程度度量的方法。本文的试验中选取天气和人口的数据集为数值型的数据,依据其数值的大小进行相似程度的衡量,而像文本这样的数据集为字符串型的数据,依据其字符串的长度对其相似程度进行衡量。本文将分布式数据真值发现同几个常用的真值发现算法,如Vote、ACCUVOTE、Estimates等进行比较,并根据每个算法的特性对参数进行调整,选取最优结果来进行比较。
4.3实验数据集
本文选取供电局都采用的能量管理系统(EMS)集控中心的变损、线损和负载损耗三个真值的数据集进行实验并利用输出结果进行比较。三者的数据集为数值型的数据,满足多级空间值定义,各级别之间的独立性比较明显。“真实集”即真实值,其表明了由人工校准的方式筛选出的于数据集相对应的正确的数据项值的数量,各个算法的配适率则是通过将真实集同算法的输出结果进行比较得出。具体描述了这三类数据集的详细统计信息如表2所示。
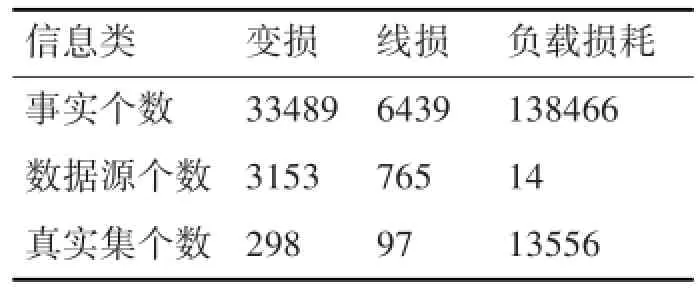
表2 电网信息真实数据集统计
4.4结果分析
具体的算法准确率与时间开销如表4所示。

表4 不同算法的准确率与时间开销统计
由表3的准确率P可以看出,分布式数据真值发现在线损数据集挖掘上拥有出色的表现,比AC⁃CUVOTE算法的配适准确率高出4.1%。由于分布式数据真值发现参考了ACCUVOTE的一些原则,其配适率与ACCUVOTE算法存在一定的联系,但最终实验结果相较于ACCUVOTE算法要优越一些。而在变损和负载损耗数据集上,分布式数据真值发现和ACCUVOTE算法输出结果的的配适率较低。分布式数据真值发现前提条件是数值拥有多级值空间,而对于数据项的值相对都比较小的数据集而言,分布式数据真值发现的多级值空间分级并不存在发挥其优势的空间。ACCUVOTE方法输出的结果在负载损耗数据集上表现也并不如人所愿,主要是负载损耗数据集中的数据来源的数量较少而与数据集对应的真值较多由此容易引发冗余数据的产生。由于数据源之间冗余数据的数据项数量较大,它作为指数,容易导致利用ACCUVOTE算法演算数据源之间存在依赖。
由表3的时间开销与迭代次数之间的关系不难发现,Vote算法的时间耗费最小,分布式数据真值发现时间耗费较小,ACCUVOTE时间耗费次之。由于算法中需要采取迭代来计算数据源之间的依赖程度们因此需要大量的计算时间,因而时间开销较大,其中变损数据集的时间开销最为明显。
对参数α与β的调整对实验结果会产生影响,具体的结果如图1和图2所示。

图1 不同α调整分布式真值发现准确率
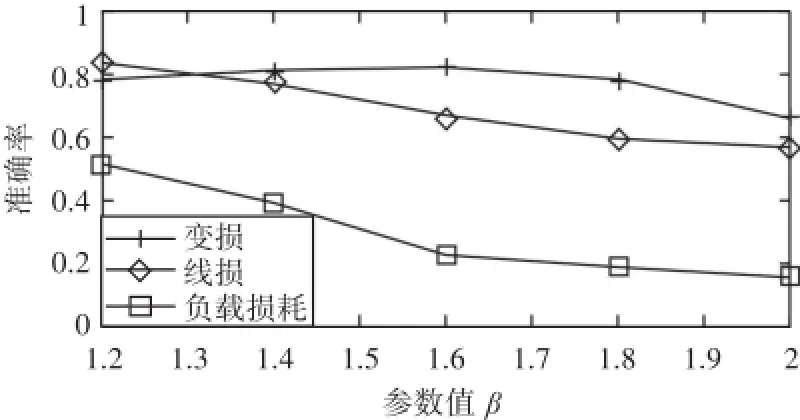
图2 不同β调整分布式真值发现准确率
根据图1中描绘了在β不变且各自选取最优值的条件下,当参数α从1.5不断调整到4时,变损、线损和负载损耗三个数据集在算法输出的结果中其配适率变化的曲线。当变损数据集的参数设定为2.5时,分布式真值发现的配适率最高。当线损数据集的参数设定为1.5时,各个“级别”之间的独立性较强,不存在拆分的关联原则,导致各个级别之间的权重比越大因此结果也越差。当线损数据集的参数设定为2时,结果最优。图2中描绘了在α不变且各自选取最优值的条件下,当参数β从1.2不断调整到2时,三个数据集在算法输出的结果中其配适率变化的曲线。参数均取为1.2时,线损和负载损耗数据集各个级别之间的权重比越低,结果最优。当变损数据集的β取为1.6时,结果最优。
5 结语
论文针对数据管理系统中存储的多级数据真值发现问题,从多级数据源特征出发,利用数据集分级后级值与真实值相似度定义分布式迭代真值发现。通过贝叶斯公式构建不同质量的数据来源级值计算,结合级别权值迭代生成完整值并利用相似度定义不同级别之间的差异性,最终设计了一套分布式真值发现算法。该多级数据真值发现算法准确率高,可为数据信息管理系统的数据分类与挖掘提供一种新的途径。
[1]杨志.一种实时大数据查询技术-对象分布式查询[J].计算机与数字工程,2015(10):1851-1856.
YANG Zhi.A Real-Time Big Data Query Technology-Objects Distributed Queries[J].Computer&Digital Engi⁃neering,2015(10):1851-1856.
[2]付仲良,刘思远,田宗舜,等.基于多级R-tree的分布式空间索引及其查询验证方法研究[J].测绘通报,2012(11):42-46.
FU Zhongliang,LIU Siyuan,TIAN Zongshun,et al.Meth⁃od of Distributed Spatial Indexing and Query Authentica⁃tion Based on Multi-Level R-Tree[J].Bulletin of Surcey⁃ing and Mapping,2012(11):42-46.
[3]张涛,余炀,李弋.Linux服务器安全审计系统的设计与实现[J].计算机应用与软件,2014(5):17-22.
ZHANG Tao,YU Yang,LI Ge.Design and Implementa⁃tion of Linux Server Security Audit System[J].Computer Applications and Software,2014(05):17-22.
[4]李天义,谷峪,马茜,等.一种多源感知数据流上的连续真值发现技术[J].软件,2016(7):341-349.
LI Tianyi,GU Yu,MA Qian,et al.A multi-Source-Aware Continuous Stream on the True Value of Data Discovery Technology[J].software.2016(7):341-349.
[5]张志强,刘丽霞,谢晓芹,等.基于数据源依赖关系的信息评价方法研究[J].计算机学报,2012,35(11):2392-2402.
ZHANG Zhiqiang,LIU Lixia,XIE Xiaoqin,et al.Evalua⁃tion Method of Information Based on the Data Source De⁃pendency[J].Journal of Computers,2012,35(11):2392-2402.
[6]马如霞,孟小峰.基于数据源分类可信性的真值发现方法研究[J].计算机研究与发展,2015(9):1931-1940.
MA Ruxia,MENG Xiaofeng.Credibility of the Discovery of the True Value Based on the Data Source Classification[J].Research and Development of Computer,2015(9):1931-1940.
[7]唐向红,李国徽,杨观赐.快速挖掘数据流中离群点[J].小型微型计算机系统,2011,32(1):9-16.
TANG Xianghong,LI Guohui,YANG Guanci.Fast Mining Data Stream Outliers[J].Journal of Chinese Computer Sys⁃tems,2011,32(01):9-16.
[8]祝然威,王鹏,刘马金.基于计数的数据流频繁项挖掘算法[J].计算机研究与发展,2011,48(10):1803-1811.
ZHU Ranwei,WANG Peng,LIU Majin.Data Stream Min⁃ing Algorithms Based on Frequent Item Count[J].Re⁃search and Development of Computer,2011,48(10):1803-1811.
[9]余祖坤,许景楠,郑小林,等.基于信任的真实数据判定方法[J].系统工程理论与实践,2013,33(9):2404-2414.
YU Zukun,XU Jingnan,ZHENG Xiaolin,et al.Real Data Determination Method Based on Trust[J].Systems Engi⁃neering Theory and Practice,2013,33(9):2404-2414.
[10]廖国琼,吴凌琴,万常选.基于概率衰减窗口模型的不确定数据流频繁模式挖掘[J].计算机研究与发展. 2012,49(5):1105-1115.
LIAO Guoqiong,WU Linqin,WAN Changxuan.Mining Model Based on Probability Attenuation Window of Un⁃certain Data Stream Frequent Pattern[J].Research and Development of Computer,2012,49(5):1105-1115.
[11]王继奎,李少波.多数据源冲突的主数据真值发现算法[J].计算机工程与设计,2014,35(1):177-182.
WANG Jikui,LI Shaobo.Master Data Multiple Data Sources Conflicts True Value Discovery Algorithm[J]. Engineering and Design of Computer,2014,35(1):177-182.
[12]郭继东,李学庆,杨成伟.基于子空间的鲁棒射影重建方法[J].计算机学报,2013,36(12):2560-2576.
GUO Jidong,LI Xueqing,YANG Chengwei.A Robust Subspace Algorithm for Projective Reconstruction from Multiple Images[J].Journal of Computers,2013,36(12):2560-2576.
[13]刘畅,唐达.一种改进的加权随机抽样算法[J].软件,2011,32(1):14-17.
LIU Chang,TANG Da.An Improved Algorithm of Weighted Random Sampling[J].Computer Engineering &Software,2011,32(1):14-17.
Multi-level Data True Value Discovery Based on Distributed Technology
LV WeixinYIN Jun
(Yunnan Power Grid Co.,Ltd.Kunming Power Supply Bureau,Kunming650200)
To further enhance the reliability and accuracy of the data management system,this study presents a multi-level data based on distributed technology discovered the true value of mining and eliminates the difference between the level of indepen⁃dence.This method grades the data phase values of data source and use level values and the real value of the defined similarity itera⁃tive accuracy to avoid the same data is extracted in a different level when differences.By distributed technical mining algorithm the probability of level values and the degree of deviation are calculated to determine the true value of the multi-level data.Finally,through the overlapping data sets of experiments the efficiency of multi-level data true value discovery is illustrated.
multi-level data,true value discovery,distributed,data mining
TN919.3
10.3969/j.issn.1672-9722.2017.05.030
2016年11月7日,
2016年12月19日
国家自然科学基金资助项目(编号:51277085)资助。
吕维新,男,高级工程师,研究方向:云计算。殷军,男,工程师,研究方向:信息技术与信息管理,计算机技术。

