基于非线性输出反馈的三自由度直升机控制∗

基于非线性输出反馈的三自由度直升机控制∗

周唯王晓东

（昆明理工大学信息工程与自动化学院昆明650500）

针对三自由度直升机系统的控制系统，提出了基于非线性输出反馈的处理方法。通过机理分析建立了三自由度直升飞机的数学模型，使用微分几何中仿射非线性局部同胚坐标变换理论把系统的俯仰轴和滚动轴两个通道精确线性化处理，得到解耦的、正则的线性系统。利用线性最优二次型（LQR）理论设计了线性化处理后跟踪控制器，同时对旋转轴设计了PID控制器。仿真和实验结果表明，论文使用的非线性反馈处理方法是有效的。

非线性；输出反馈；精确线性化；线性二次型控制；PID控制

Class NumberV275.1

1 引言

本文是基于三自由度直升机开展的研究。三自由度直升机具有多输入多输出、高阶次、强耦合、非线性等特点。为了获得对直升机更好的控制品质，需要对直升机的建模和控制器进行研究。文献［1～8］提出针对控制对象的系统辨识方法对系统建模。系统辨识方法主要依据系统辨识理论和实验，最小二乘参数辨识、极大似然参数辨识、神经网络辨识等都应用得比较成熟，但是对于多输入多输出系统建模过程就比较复杂。因此常采用近似线性化处理方法，该方法主要根据直升机的动力学模型在工作点附近做Taylor展开，取线性局部近似。缺点是建立的模型精度不够，在后期的应用中很大程度上依赖于控制器的鲁棒性对系统未建模部分进行系统镇定。文献［9］提出基于奇异系统状态反馈鲁棒控制器设计方法。文献［10］基于LQR和H∞的三自由度直升机多模型控制器设计，多模型设计比较繁琐。文献［11］把建模的不精确看成系统的不确定性干扰，设计了基于LMI的直升机鲁棒飞行控制器。本文提出的非线性状态反馈线性化方法可以实现非线性强耦合的三自由度直升机系统的线性化和解耦控制。这种方法相比系统辨识方法更简洁，省去了繁琐的实验和繁琐的数据处理，相比局部近似化处理，可以在更大的控制范围内得到很好的控制效果。

2 三自由度直升飞机系统建模

三个维度上的运动模拟的是纵列式双旋翼结构直升机，美国的中型运输直升机（支奴干CH-47）就是代表。如图1所示，三自由度直升飞机研究平台由直升机本体、俯仰机架杆、重力块、偏航机架杆、基座、集电环、三个角度传感器组成。直升机本体由两个螺旋桨电机驱动叶片提供直升机系统运动的动力。俯仰机架杆两端分别连接重力块和直升机本体。偏航轴机架杆支撑俯仰轴机架杆。三个角度传感器实时测量系统在俯仰、滚动、偏航这三个维度上的角度。定义三自由度直升机的俯仰角（Pitch）为α，滚动角（Elevation）为θ，偏航角（Travel）为ϕ。安装在基座中的集电环保证了直升机本体和控制台之间的信号传送不受直升机转动的影响。三自由度直升机实验平台的控制目标是俯仰角度，旋转角度的跟踪，同时控制滚动角度在一定的范围。取俯仰轴水平时α=π/2rad，滚动轴水平时θ=0rad，旋转角初始位置ϕ=0rad。

图1 三自由度直升机示意图和实物图

2.1俯仰轴（Elevation axis）建模

俯仰运动是靠前向电机和后向电机驱动两个螺旋桨产生的升力和系统的重力在俯仰机架上产生的合力矩来驱动的。前向电机的电压输入为Vf，后向电机的输入为Vb。电机驱动螺旋桨产生的升力近似和电机的输入电压成正比例，Kf为螺旋桨产生的升力和输入电压的比值。则单个螺旋桨的输入电压V和输出升力F之间的关系：

俯仰轴的转动惯量为Je，直升机本体到俯仰轴支点距离为La，前向、后向电机的输入电压分别为Vf，Vb，俯仰轴自重产生的关于俯仰轴支点的力矩为Fgsinα。则俯仰轴的动力学方程如下

2.2滚动轴（Pitch axis）建模

前向电机和后向电机的驱动力不相等时，作用在滚动轴上的合力矩不为零，此时滚动轴被驱动。滚动轴转动惯量为Jp，电机到转轴之间的距离为Lh，直升机的升力是垂直于滚动轴的。则滚动轴动力学方程如下

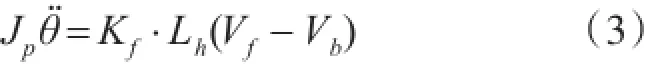
2.3旋转轴（Travel axis）建模

直升机的旋转运动是由于在直升机产生俯仰角后在水平面产生了相对于旋转轴的力矩，此力矩使直升机在水平面转动。直升机旋转轴转动惯量Jt=Je，旋转平面上的受力是Kf(Vf+Vb)sinθ，受力点到旋转轴距离为La，力的方向与旋转轴之间的夹角为α。则旋转轴的动力学方程如下

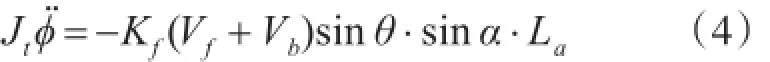
在直升机的实际控制中首先是控制俯仰角稳定，再次控制旋转角。这样在控制旋转角时方程（2）是稳定的，有如下方程：

把方程（5）代入方程（4）可得：

综上所述，三自由度直升飞机的数学模型如下：

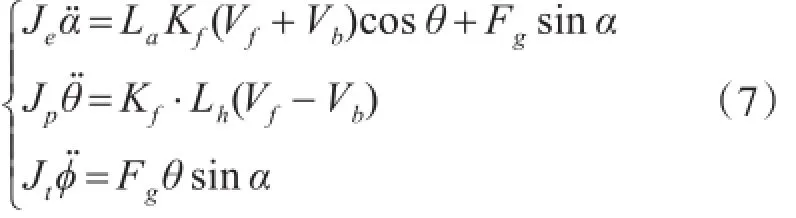
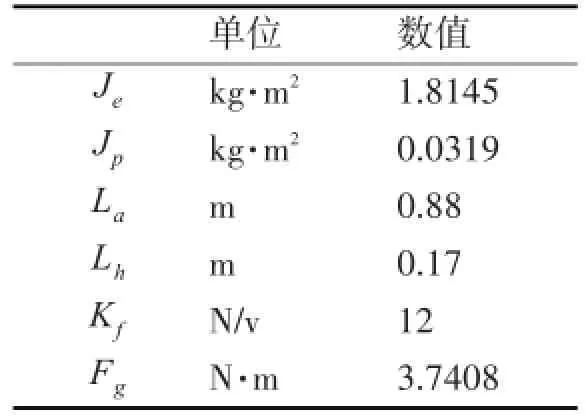
表1 系统参数

由式（7）可以看出三自由度直升机系统是一个多输入多输出、强耦合、非线性的系统。对上述系统直接设计控制器是十分困难的。通常的做法是在式（7）的基础上进行近似处理，使得系统用线性系统来近似，再利用线性系统设计的相关理论进行控制器设计。本文提出的非线性反馈的方法是在式（7）的基础上利用非线性输出反馈线性化三自由度直升机的数学模型得到解耦的线性模型，使得到的解耦的线性系统能够用成熟的线性控制理论设计控制器。

3 非线性输出反馈线性化

本文使用的是基于微分几何理论的非线性输出反馈线性化方法，又称精确线性化方法。非线性输出反馈在实现中针对输入和输出数量不相等的系统来说处理起来比较复杂［12］。输入和输出相等的非线性系统的线性化处理的问题可以如下：

定理：给定的一个仿射多输入多输出非线性系统

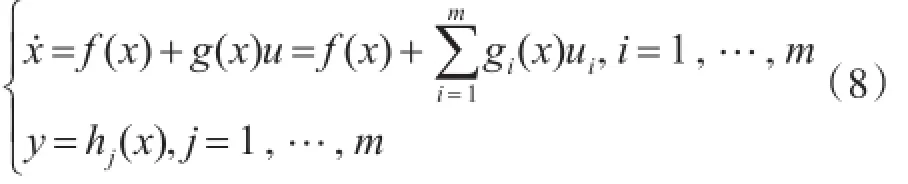
对给定的x0∈X，如果存在x0的领域V及整数向量(r1,…,rm)使满足（L是李导数符号）：

则称系统（8）在x0处具有相对阶(r1,…,rm)。

在控制率u=-A-1(x)b(x)+A-1(x)V的作用下可以线性化和解耦放射非线性系统。其中V是给定的新输入：线性化处理后得到的系统：

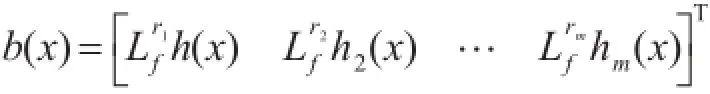
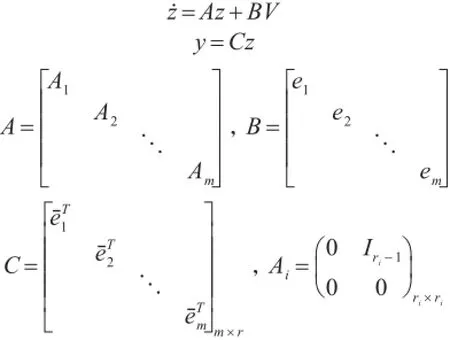
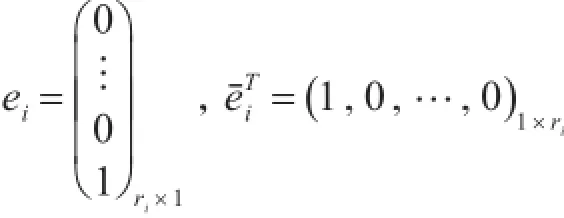
本文只针对俯仰角和滚动角进行线性化处理，是二输入和二输出系统。把三自由度直升机模型（7式）改写成式（8）的仿射非线性形式：其中状态x=[x1x2x3x4]=[α aθ θ]。

假设系统的相对阶r=[22]，下面验证系统的相对阶：

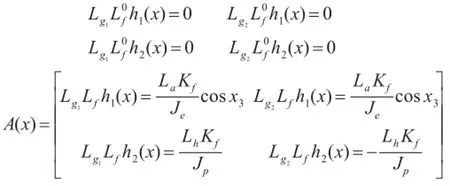
在一定的控制范围中，俯仰角在±30°，滚动角±15°，A(x)为非奇异矩阵。

系统满足假设提出的相对阶，可以进行线性和处理三自由度直升机的仿射非线性模型。由反馈构成的控制率：u=-A-1(x)b(x)+A-1(x)V，其中V是给定的新参考输入。

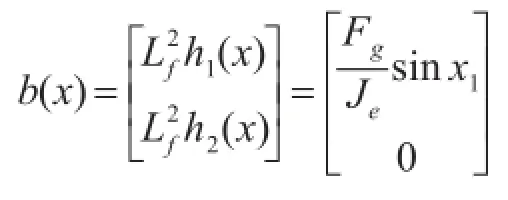
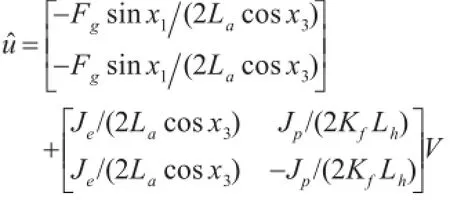
加入非线性输出反馈，经过坐标变换之后的系统可以表示成如下解耦的线性系统，输入V=[v1v2]如图2所示。

图2 系统线性化处理结构

加入非线性输出反馈后，在三自由度直升机模型中，系统输入v1单独控制俯仰角，输入v2单独控制滚动角。至此一个两输入两输出的非线性强耦合系统变成了一个线性的、解耦的线性系统。

4 控制器设计

前面实现了系统的部分线性化和解耦处理，通过验算得出系统（9）是一个不稳定的系统。需要再次设计控制器使得系统稳定，首先对式（9）设计LQR无限时间跟踪控制器，再对旋转轴设计PID控制器［13］。

4.1最优二次型无限时间定常跟踪控制器设计

利用最优二次型（LQR）无限时间定常跟踪控制器，可以方便地设计针对线性系统的跟踪控制器。在线性时不变条件下，设计的LQR无限时间定常跟踪控制器是一个近似的控制器［14］。

经过验算，系统（9）是一个完全能控制完全能观的系统。yl为希望输出，e(t)为误差向量，误差e(t)=yl-y(t)，性能指标：

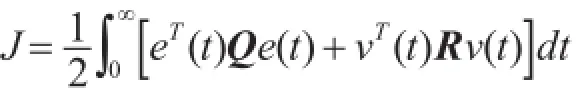
其中Q和R都是正定的常数矩阵。则系统的近似最优控制率为

其中S是黎卡提代数方程（10）的解：

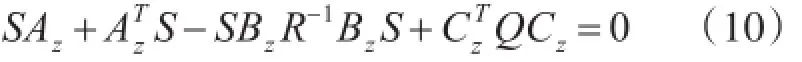
考虑控制效果选择Q=diag（［50 10］），R=di⁃ag（［1 1］），这样俯仰轴和滚动轴的控制器设计完成。4.2旋转轴PID控制器设计

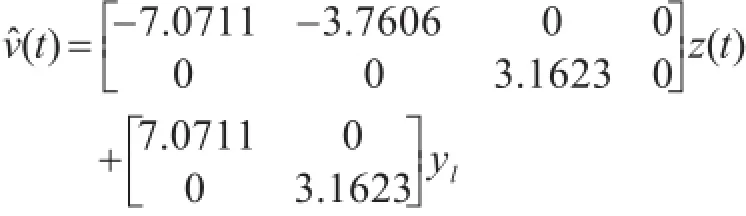
可以把方程（6）右端滚动角θ看成式（6）的输入，则简化后的表达式JtΦ=Fgθ，进行拉普拉斯变换后

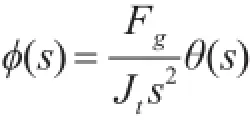
首先加入PD控制器［14］，定义旋转角误差e=ϕc-ϕ，则输入uβ=Kke+Kde，Kk为比例系数，Kd为微分系数。闭环传递函数：

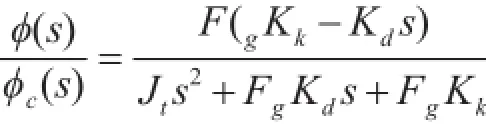
按照二阶系统响应选取阻尼比ξ=0.707设计系统PD控制器参数。再加入积分环节，实现旋转角的无静差控制。通过计算和调试选取的控制器为：Kk=0.55，Kd=1.66，Ki=1.11。

5 仿真和实验

仿真和实验均是在Matlab/Simulink环境下实现。其中仿真是在Simulink的normal模式仿真环境下实现的。实验是通过Matlab/Simulink的实时工具箱RTW（Real-Time Workshop）实现实时控制。图3所示是Simulink仿真模块，在Simulink模块中Helicopter_3DOF搭建的是三自由度直升机的非线性模型式（7），no2line用Fcn函数模块搭建非线性反馈模块（8），PID控制器模块是旋转轴PID控制器。在实验中需要把仿真中的Helicopter_3DOF模块换成控制对象的驱动模块，这样就可以按照仿真模型中的控制规律实时控制自由度直升飞机的俯仰角和旋转角。

在系统控制中受到客观的条件限制5π/18＜α＜2π/3，-π/6＜ϕ＜π/6。直升机未上电的俯仰轴π/3=1.05rad，滚动轴θ=0rad，初始条件z=［0.87 0 0 0］T。实验设定俯仰角跟踪方波高电平，底电平1.22，即俯仰轴在水平α=π/2rad在±20°内跟踪给定方波信号。滚动角设定方波跟踪信号高电平0.26，底电平-0.26，即是滚动角θ=0rad在±15°内跟踪给定信号。实验用方波周期为10s，时间20s。

图3仿真Simulink模块

图4 是非线性反馈后LQR跟踪控制器的俯仰角和滚动角仿真跟踪结果，PID跟踪控制的旋转角仿真跟踪结果。从仿真结果可以看出在三个角度单独跟踪仿真时效果良好；俯仰角和滚动角的动态响应快速，超调小；旋转角动态响应较差，调节时间长，有明显超调。

在图1所示的直升机平台上，实验分成三组进行，每组实验开始先给定俯仰角指令使俯仰角稳定，再给定旋转角指令使得旋转轴转动半圈后稳定。以此来验证本文提出的方法可以使得系统快速的稳定和跟随给定指令。

图4 跟踪仿真

根据三组实验，从数据可以看出，在直升机系统允许的角度范围内，俯仰角响应非常迅速，上升时间小于2.5s，超调量小于5%，调节时间小于3s，可以推断俯仰轴的动态响应是满足设计要求的。在给定指令使得旋转角转动半圈180°的实验中，旋转角度响应比较慢，上升时间在5s～9s之间，超调量很大在30%左右，调节时间在20s左右。

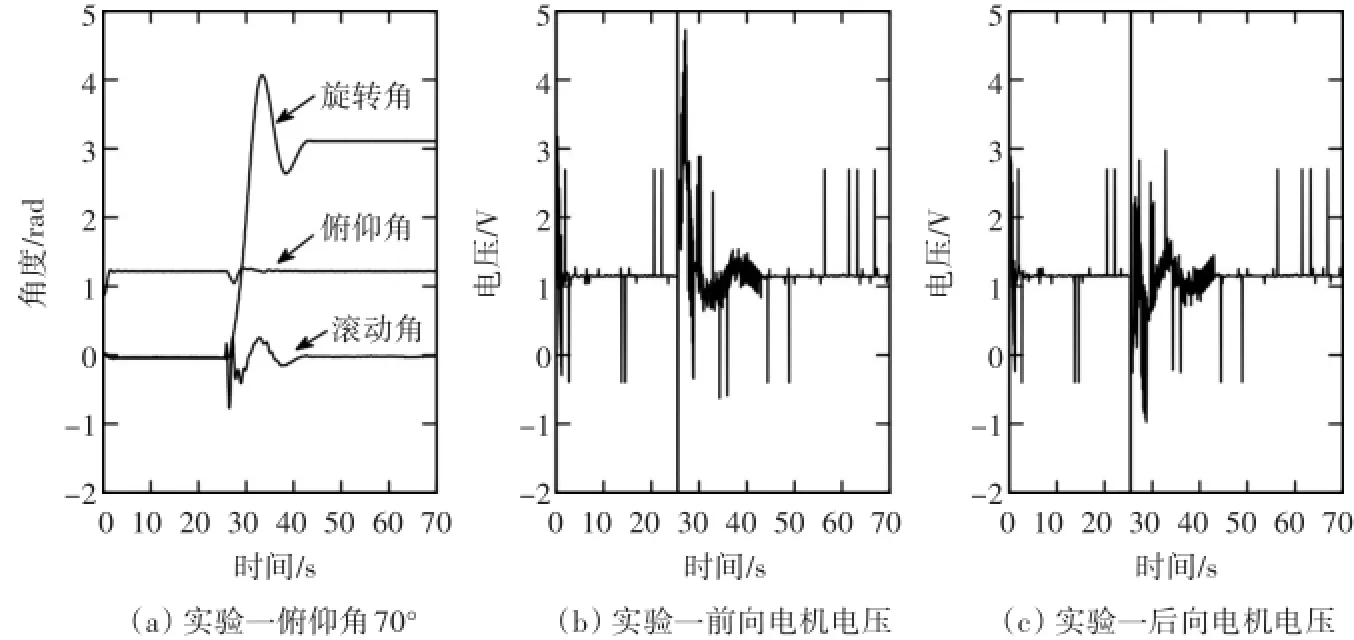
图5 俯仰轴70°、旋转轴180°

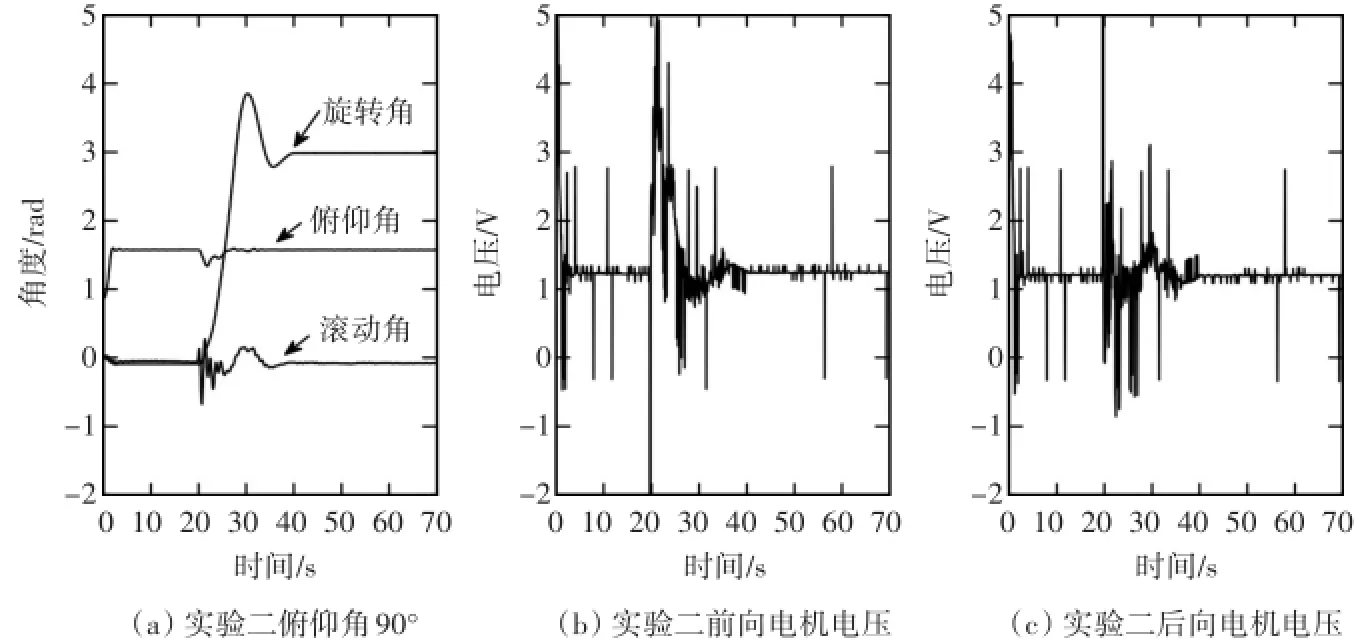
图6 俯仰轴90°、旋转轴180°

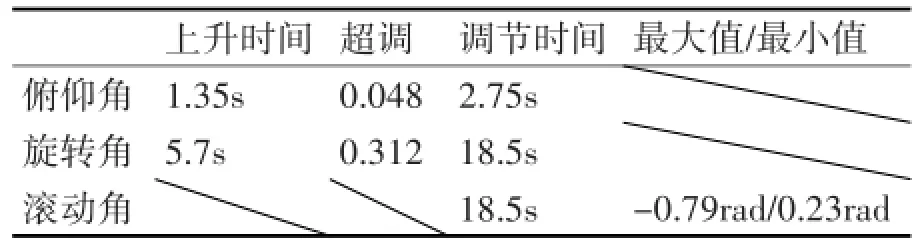
表2 俯仰角和旋转角分别给定1.22、3.14（70°、180°）

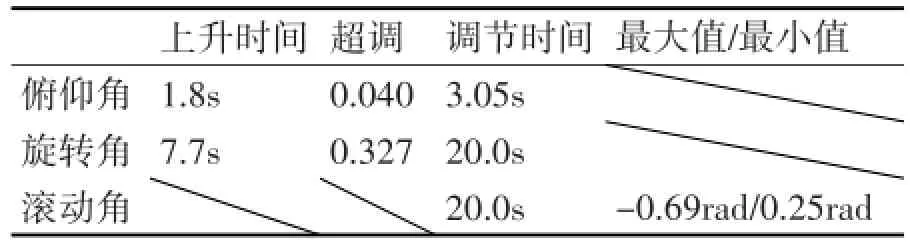
表3 俯仰角和旋转角分别给定1.57、3.14（90°、180°）

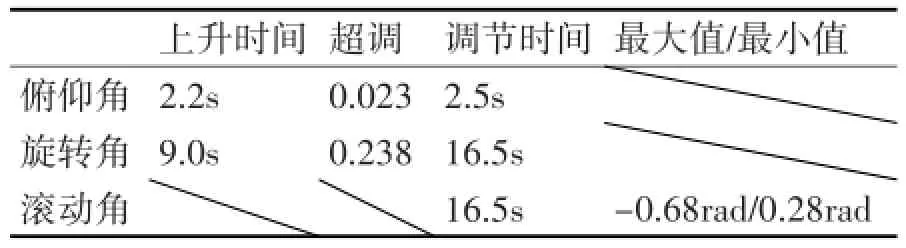
表4 俯仰角和旋转角分别给定1.92、3.14（110°、180°）

随着俯仰角度的增加，在相同的旋转角给定下，旋转角响应时间随俯仰角度增大上升时间是增大，但超调和调节时间是先增大后减小。滚动角的变化在1rad（60°）内变动，调节时间和旋转角的调节时间相等。

6 结语

根据仿真和实验结果，可以得出本文提出的非线性反馈处理的方法在三自由度直升飞机模型上是适用的。俯仰角动态响应迅速，跟踪准确；旋转角跟踪准确，单响应较慢，其原因是采用的PID控制策略的控制策略前期放大了误差，且旋转轴的阻尼很小，导致在追求旋转轴的快速性和准确性上存在着矛盾。

［1］刘克平，金晶，陈亮.三自由度直升机奇异系统鲁棒控制［J］.系统仿真学报，2011，26（6）：1238-1243.

LIU Keping，JIN Jing，CHEN Liang.Robust Control of 3-DOF Experimental Helicopter Singular System［J］.Jour⁃nal of System Simulation，2011，26（6）：1238-1243.

［2］郭帅，陆耿，钟宜生.三自由度直升机模型辨识与控制［J］.测控技术，2012，31（3）：73-76.

GUO Shuai，LU Geng，ZHONG Yisheng.Identification and Control of 3DOF Helicopter［J］.Measurement&Con⁃trol Technology，2012，31（3）：73-76.

［3］顾冬雷，高正，孙传伟.无人直升机控制动态特性的频域辨识建模方法［J］.南京航空航天大学学报，2004，36（6）：688-692.

GU Donglei，GAO Zheng，SUN Chuanwei.Frequency Do⁃main Identification for Unmanned Helicopter［J］.Journal of Nanjing University of Aeronautics&Astronautics，2004，36（6）：688-692.

［4］吴建德，李平，韩波.一种基于参数辨识的微小型无人直升机建模方法［J］.航空学报，2007，28（04）：845-850.

WU Jiande，LI Ping，HAN Bo.A Modeling Method of Min⁃iature Unmanned Helicopter Based on Parameter Identifi⁃cation［J］.Acta Aeronautica Et Astronautica Sinica，2007，28（04）：845-850.

［5］郭民环，王宇，朱欣华.固定翼无人机频率响应系统辨识技术［J］.自动化仪表，2015，36（9）：26-29.

GUO Minhuan，WANG Yu，ZHU Xinhua.Frequency Re⁃sponse System Identification Technology for Fixed-wing UAV［J］.Process Automation Instrumentation，2015，36（9）：26-29.

［6］汤剑，李中健，屈晓波.飞行控制系统辨识方法研究［J］.计算机仿真，2012，29（9）：49-53.

TANG Jian，LI Zhongjian，QU Xiaobo.Research on Identi⁃fication of Flight Control System［J］.Computer Simulation，2012，29（9）：49-53.

［7］李洁，赵佳，陈胜功，等.无人直升机辨识的一种新方法［J］.火力与指挥控制，2009，34（11）：48-51.

LI Jie，ZHAO Jia，CHEN Sheng-gong，et al.A New Sys⁃tem Identification Method for Unmanned Helicopter［J］. Fire Control&Command Control，2009，34（11）：48-51.

［8］吴伟，陈仁良.直升机纵横向耦合动力学模型的参数辨识方法研究［J］.振动工程学报，2009，22（3）：233-236.

WU Wei，CHEN Renliang.Identification method of longi⁃tudinal and lateral coupled dynamic model for helicopter［J］.Journal of Vibration Engineering，2009，22（3）：233-236.

［9］欧阳慧珉，佐野滋则，等.基于LMI的旋转起重机鲁棒控制器设计［J］.振动与冲击，2014，31（1）：107-112.

OUYANG Huimin，SANO Shigenori.Robust Controller De⁃sign for Rotary Cranes Based on LMI［J］.Journal of Vibra⁃tion and Shock，2014，31（1）：107-112.

［10］刘志超.基于LQR和H∞的三自由度直升机多模型控制器设计［D］.上海：华东理工大学，2014.

LIU Zhichao.3-DOF Helicopter Mult-model Controller Design Based on LQR and H∞［D］.Shanghai：East China University of Science and Technology，2014.

［11］代冀阳，毛剑琴.基于LMI的直升机鲁棒飞行控制及仿真研究［J］.系统仿真学报，2001，13（5）：576-578.

DAI Jiyang，MAO Jianqin.LMI-based Design and Simu⁃lation of Robust Flight Control System of Helicopters［J］Journal of System Simulation，2001，13（5）：576-578.

［12］Kreund E.The structure of decoupled non-linear systems［J］.International Journal of Control，1975，21（3）：443-450.

［13］Andrievsky B，Fradkov A.Combined adaptive autopilot for an UAV flight control［C］//International Conference on Control Applications.IEEE，2002：290-291.

［14］黄婧.三自由度直升飞机模型的模糊PID控制方法研究［D］.哈尔滨：哈尔滨理工大学，2014.

HUAN Jing.Research on Fuzzy-PID Control Method of Three-DOF Helicopter Model［D］.Harbin：Harbin Insti⁃tute of Technology，2014.

Control of 3DOF Helicopter Based on Nonlinear Output Feedback

ZHOU WeiWANG Xiaodong
（Faculty of Information Engineering&Automation，Kunming University of Science and Technology，Kunming650500）

For the control system of three degree of freedom helicopter system，a method based on nonlinear output feedback is proposed.Through the mechanism analysis，a mathematical model of three degree of freedom helicopter is established.Using the differential geometry of affine nonlinear local homeomorphism coordinate transformation theory the system of elevate axis and pitch axis two channel exact linearization processing，are decoupled，regular linear systems.Based on the linear quadratic regulator（LQR）theory，the tracking controller is designed for the linear system，and the PID controller is designed for the travel axis.Simu⁃lation and experimental results show that the nonlinear feedback processing method is effective in this paper.

nonlinear，output feedback，exact linearization，linear quadratic regulator，PID control

V275.1

10.3969/j.issn.1672-9722.2017.05.027

2016年11月1日，

2016年12月20日

云南省科技计划项目（编号：2015ZC005，2013DH034）；云南省中青年学术和技术带头人后备人才培养计划项目（编号：2011CI017）资助。

周唯，男，硕士研究生，研究方向：向非线性控制、鲁棒控制。王晓东，男，博士，教授，研究方向：基于数据驱动的工业过程控制、多源信息融合技术、基于数据挖掘的智能检测技术。