G-W序列相关性研究及在扩频通信中的应用∗

G-W序列相关性研究及在扩频通信中的应用∗

张野

（92124部队大连116023）

应用序列代数和的概念，对零相位差处复合G-W序列的良好的代数和相关性进行分析，进一步讨论了非零相位差处G-W序列代数和相关的多值特性。针对G-W序列代数和良好的代数和相关特性，并行组合扩频系统在序列非同步情况下建立仿真模型，结果表明G-W序列集可实现并行组合扩频系统的序列自同步。

G-W序列；相关性；并行组合扩频系统；序列同步

Class NumberTN914

1 引言

在拥有强干扰和噪声抑制能力、强多址通信能力等技术优势的基础上，并行组合扩频技术解决了直接扩频通信技术传输效率较低的缺点，受到很多学者专家多方面关注。当前，该领域研究主要集中在并行组合扩频和其他技术的结合［1］，并行组合扩频技术的调制［2］，并行组合扩频在不同通信环境中的应用［3］等方面。区别于直接序列扩频系统传输的单一扩频序列，并行组合扩频系统传输的是并行组合序列，组合伪随机序列是并行组合扩频技术的核心组成，寻找和构造满足需求的伪随机序列是工程应用中的关键问题，Walsh序列以其零相关处良好的正交相关性而备受重视，但因其非零相位差处相关性较差的缺点令其应用受限。而Gold序列拥有数量大，良好的统计特性的明显优点，在工程中被大量使用。一种由Walsh和Gold复合而成的G-W序列，综合了两种序列各自的优点被广泛应用在认知无线电环境中实现频谱可控，也用于通信测距中以适应各种信道模式［4～5］，因复合处理后其序列集中序列数目较多，复合序列更可用在多址通信中。由此，进一步对组合G-W序列相关性的研究对其在并行组合扩频技术中的应用更有着重要的意义。本文采用了序列代数和的概念对G-W序列进行了分析，为并行组合扩频技术中序列同步提供了良好的理论基础，并进行了同步仿真，验证了G-W序列在非同步并行组合扩频系统中具有良好的可靠性。

2 代数和相关性的概念

文献［6］针对并行组合扩频系统中组合序列并行传输的特点，提出了代数和序列相关性的概念。在并行组合扩频系统中应用代数和序列相关性分析序列相关性更准确，可以为接收端序列解扩、序列间互干扰以及序列自同步提供良好的理论基础。

扩频序列集由{A1},{A2},…,{Al},…,{AM}组成，设序列周期长度为N，设{Al}中的第i个码元为ail（其中1≤i≤N,1≤l≤M）。从序列集中取r条序列，并乘以权系数ql后叠加生成序列{B}，{B}中第i个码元为bi：

其中，权系数ql∈{+1,0,-1}用于控制序列的极性。若{B}中序列由{Al}和其它序列叠加生成，则{Al}和{B}两序列的代数和自相关函数为

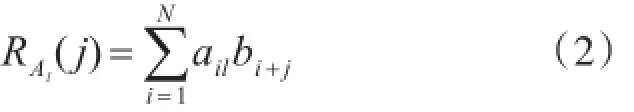
序列{Al}和{B}的代数和自相关系数定义为

若{B}中序列不是由{Al}序列参与叠加生成时，则{Al}和{B}两序列的代数和互相关函数及互相关系数也由式（2）和式（3）表示。

组合序列{B}和序列{Al}的代数和自相关函数实际上是{Al}的自相关函数以及{Al}与其它参与构成{B}的序列互相关函数的加权和，权系数由参与构成{B}的序列的r个极性选取因子确定。由伪随机序列的相关性可以推知以下组合序列的代数和相关性：

1）如果序列集中各序列自相关特性良好，并且彼此正交，那么代数和自相关系数在零相位差处为1。

2）若序列集中序列彼此正交，则组合序列与集内不参与构成组合序列的其他序列的代数和互相关系数在零延时处必为0，而与组合序列的构成序列个数r无关。即若在并行组合扩频系统中使用正交序列集进行扩频，则发送端映射后得到的组合序列和其他序列仍存在正交性。

组合序列的代数和相关特性是依据参与构成的序列加权系数及其序列自有相关特性求得的，所以在一定程度上，组合序列的代数和相关特性上继承了各参与构成序列的相关特性。但单一序列的相关性仅能定性分析组合序列的相关性，而组合序列的相关性可由代数和相关性来进行定量计算，所以关于代数和相关特性在并行组合扩频系统中的研究是十分必要的。

3 G-W序列的构成及其代数和相关性

Gold序列继承了m序列的诸多优点，且可用的序列条数远大于m序列，用Gold序列替换m序列作为外码，Walsh序列作为内码构造出G-W复合序列，其复合方法与生成m-W序列的构造方法一样［7～8］。

考虑到过渡季节及冬季极寒天气情况下，系统的切换运行及匹配性，冷冻站共设4台冷水机组，其中750RT（约2638kW）离心式冷水机组3台，450RT（约1582kW）螺杆式冷水机组1台，工艺冷冻水平时使用1台，空调用冷冻水平时使用2台，剩余1台螺杆机，根据具体运行工况进行切换。

因同族Gold和同族Walsh序列数目均较多［9］，G-W序列构成情况为1条Walsh和同族Gold序列构成的G-W序列以及1条Gold序列和同族Walsh序列构成的G-W序列，本文仅讨论Gold序列族构成的G-W序列。

若Gold序列的周期长度为Ng，Walsh序列的周期长度为Nw，则Ng与Nw必为互素。G-W复合序列的周期长度为Ngw=NgNw，由Gold序列族为主体，引入Walsh序列构造的G-W序列的相关函数(j)为

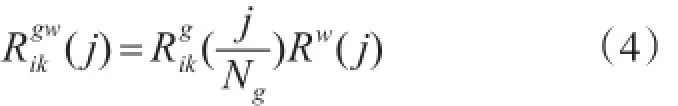
这说明G-W序列在零相位差处序列间并非完全正交，而是呈现类正交的相关特性。设G-W序列由周期为Nm=63的一族平衡Gold序列和随机抽取的一条周期Nw=8的Walsh序列构成，其周期Ngw=504。可构成的G-W序列族中序列个数L=49条，大幅度提高了复合序列的条数。从中任取4条序列{A1}、{A2}、{A3}、{A4}研究其自相关及其互相关特性，图1为序列{A1}的自相关系数及其与其他序列的互相关系数图。

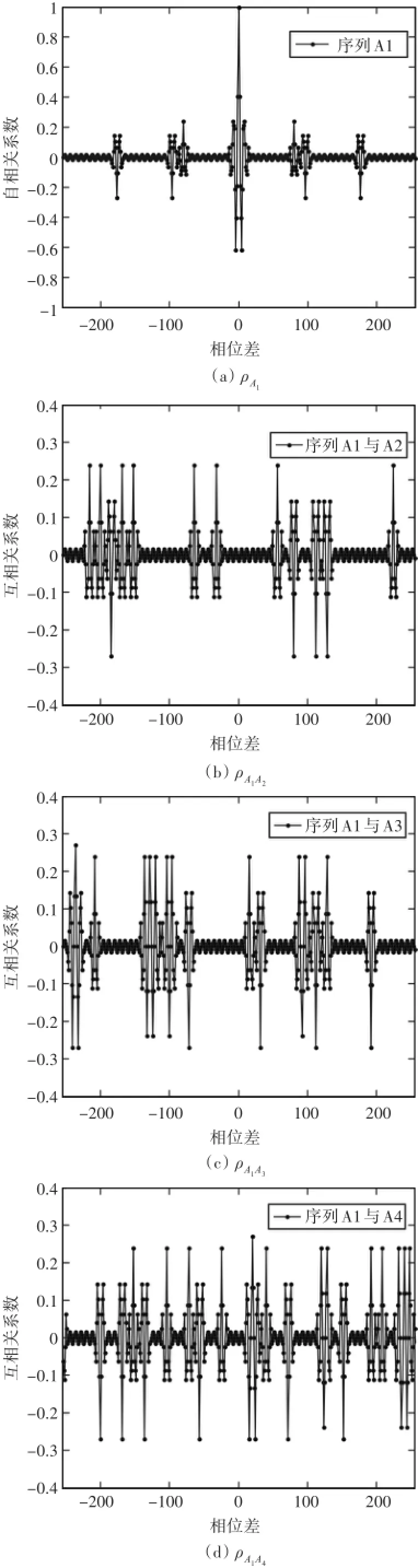
图1 序列{A1}的相关特性

由图1可知在零相位差处G-W序列的自相关系数为1，有尖锐的相关峰值，互相关系数为-0.0159，序列间近似正交，满足式（4）计算出的理论数值。从图1（a）中可以看出G-W序列自相关系数包络在零相位差处有尖锐的最高峰值，而其他时延处呈现多峰值特性。而图1（b）～（d）可见G-W序列的互相关系数包络呈多值特性，但其峰值均不超过0.3，G-W序列互相关特性良好，可见G-W序列的相关性一定程度上继承了Gold序列的相关性。

依据组合序列定义，r个G-W序列乘以极性控制因子叠加后得到组合序列{B}。若参与构成组合序列{B}的r个序列中极性控制因子qm=1的序列个数为m，那么qm=-1的序列个数则为(r-m)。G-W序列零相位差处的代数和自相关函数可表示为

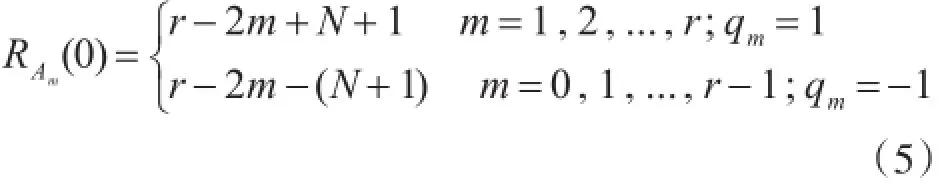
而序列{B}与序列集内其余G-W序列的代数和互相关函数可表示为

可求式（5）的极值，并取其绝对值，则其代数和自相关系数最大值|ρAm(0)|取值范围为

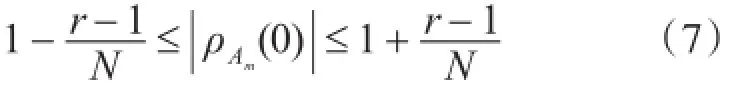
则其代数和互相关系数取值范围为

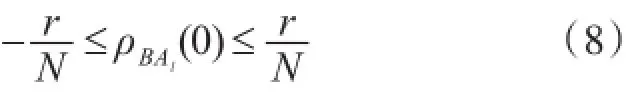
进一步可推知，用G-W序列零相位差处的代数和互相关系数取值也满足两两近似正交。设序列{B}={A1}+{A2}+{A3}，讨论G-W序列的代数和相关特性。图2为G-W序列的代数和自相关系数和代数和互相关系数示意图。

应用式（7）中理论分析，可知G-W序列的代数和自相关系数也满足零相位差处G-W序列的代数和自相关系数有尖锐峰值为0.9683，满足理论峰值；且应用式有零相位差处G-W序列代数和互相关系数满足图中序列零相位差处代数和互相关系数为0.0467，也满足理论推导。G-W序列在非零相位差处代数和自相关和互相关系数峰值也较多，且呈现峰值较大的特性，无法定量分析。

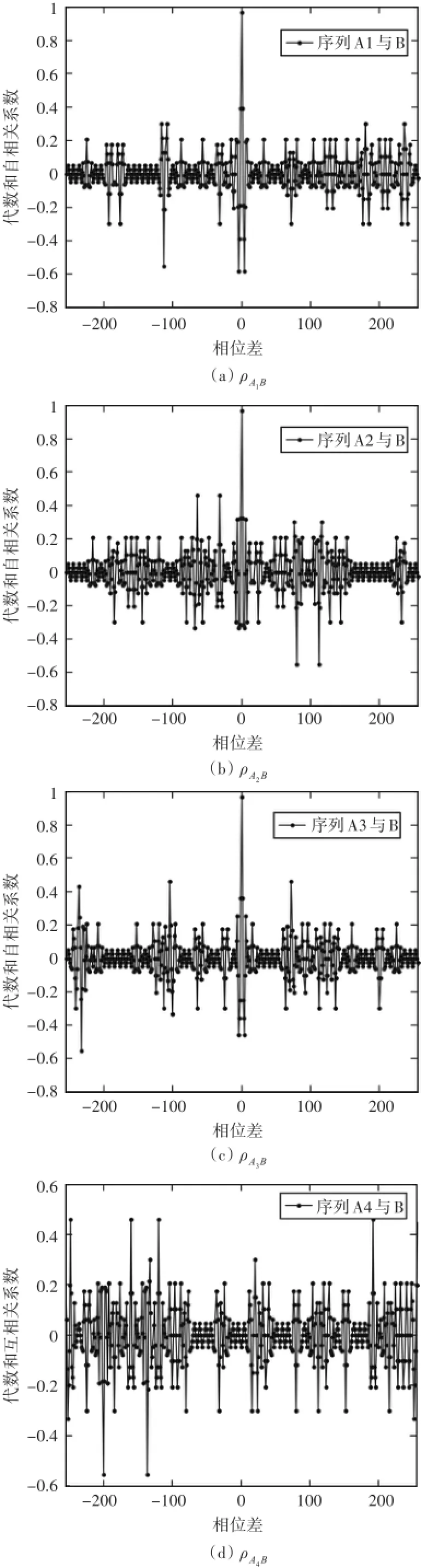
图2 {B}序列的代数和相关特性

由图2也可见Gold序列代数和互相关系数也取多值，并有多个旁瓣峰值，较一般的Gold序列互相关特性严重下降，但相对于其他序列其代数和相关性性能还是比较优越的。进而扩展了并扩系统当中序列自同步过程中可应用的序列种类。

4 G-W序列在并行组合扩频系统中的应用

在并扩系统发射端将k比特信息进行串并转换，并行送入数据-序列组合映射器，根据序列组合-数据映射算法，将r条不同序列从M条序列{PNi}(i=1,2,…,M)中选出，并考虑序列极性，取qi∈(0,-1,+1),(i=1,2,…,M)，相应码片等幅度叠加形成多值组合序列：

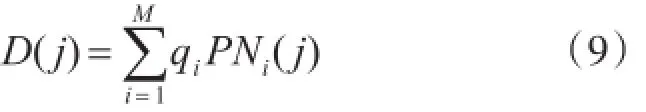
式中，qi为序列极性，表示序列选取的控制因子；qi=0时为映射时不选其对应序列{PNi}；qi=±1为映射时选取序列{PNi}，其符号表示序列选取正负极性。

并扩系统中，每次发送的信息量k为

并行组合扩频系统中，本地扩频序列在接收端与接收序列进行相关解扩后，按照序列组合-数据逆映射算法，从M个相关器输出值中选出绝对值最大的r个，结合其极性信息，经过并串转换还原出发送的信息［10］。

在并行组合扩频系统中，若想实现组合序列的正确捕获需将组合序列和所有本地序列分别进行相关运算才能得出零相位差处尖锐的自相关值，根据G-W序列良好的代数和相关性，将其应用在并行组合扩频系统无噪情况中，G-W复合序列周期长度为504。图3为扩频序列总数M=16，r=2以及r=3时系统序列的捕获概率；图4为扩频序列总数r=3，M=16以及M=32时的捕获概率。其中每个扩频码元采样点为TC2。可以发现，无论r取何值，M越大则捕获概率越高；无论M取何值，r越大则捕获概率越高。

图3 同r条件下选取发射的序列数M对捕获概率的影响

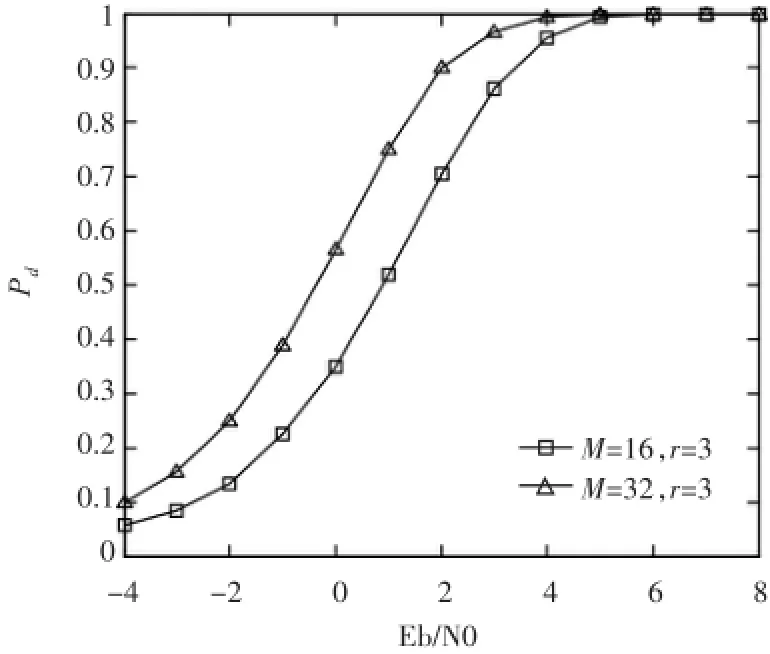
图4 同M条件下选取发射的序列数r对捕获概率的影响

5 结语

本文对复合G-W序列的相关性以及代数和相关性进行了分析，针对G-W序列非零相位差处拥有良好相关性的特点，将其用于并扩系统组合序列同步中，并在无噪声情况下对序列同步的捕获概率进行了仿真，验证了G-W序列在非同步并行组合扩频系统中应用的可行性。同时，得出了组合序列捕获概率和选取的扩频序列数r成正比，和系统扩频序列总数M成正比的结论。

［1］QI Lin，GUO Lili，JIANG Xiaofei.Performance Studies of UWB Communication System Based on Parallel Combina⁃tory Spread Spectrum［C］//Wireless Communications，Net⁃working and Mobile Com，2009：1-4.

［2］王玫.短波并行组合扩频通信系统关键技术的研究［D］.哈尔滨：哈尔滨工程大学，2009：3-4.

WANG Mei.Study of Key Techniques for Shortwave PCSS Communication System［D］.Harbin：Harbin Engineering University，2009：3-4.

［3］殷敬伟，王蕾，张晓.并行组合扩频技术在水声通信中的应用［J］.哈尔滨工程大学学报，2010（7）：958-962.

YIN Jingwei，WANG Lei，ZHANG Xiao.The Application of Parallel Combinatory Spread Spectrum in Underwater Acoustic Communication［J］.Journal of Harbin Engineer⁃ing University，2010，31（7）：958-962.

［4］郭黎利.基于互补序列的通信测距复合系统关键技术研究［D］.哈尔滨：哈尔滨工程大学，2005：15-16.

GUO Lili.Key Technologies of Communication and Loca⁃tion Complex Systems Based on Complement Seuqences［D］.Harbin：Harbin Engineering University，2005：15-16.

［5］李春晖.基于m序列与Walsh序列的复合序列［J］.佳木斯教育学院学报，2010（5）：160.

LI Chunhui.Composite sequence based on m sequence and Walsh sequence［J］.Journal of Jiamusi Education In⁃stitute，2010（5）：160.

［6］姜晓斐.并行组合扩频超宽带通信系统的关键技术研究［D］.哈尔滨：哈尔滨工程大学，2012：12-15.

JIANG Xiaofei.Research on Key Technologies of UWB Communication Systems based on Parallel Combinatory Spread Spectrum［D］.Harbin：Harbin Engineering Univer⁃sity，2012：12-15.

［7］吴海红.CDMA扩频通信中m序列与Gold序列的比较及应用［J］.喀什师范学院学报，2010（3）：39-43.

WU Haihong.Comparison and Application of in CDMA Wide Frequency Correspondence m Sequence and Gold Sequence［J］.Journal of Kashgar Teachers College，2010（3）：39-43.

［8］郭黎利，付江志，崔永生，等.采用m-W复合序列的直扩系统规避窄带干扰的研究［J］.哈尔滨工程大学学报，2010，（5）：646-651.

GUO Lili，FU Jiangzhi，CUI Yongsheng，et al.Using m-Walsh composite sequences to reduce narrow-band in⁃terference in direct sequence spread spectrum systems［J］. Journal of Harbin Engineering University，2010，31（5）：646-651.

［9］Mykhaylenich P.The research of sequence partial ensem⁃bles application in MC-CDMA system［C］//Modern Prob⁃lemsofRadioEngineeringTelecommunica，2012：253-253.

［10］郭黎利，刘佳鑫，李北明，等.并行组合扩频组合伪码捕获算法研究［J］.遥测遥控，2014（3）：1-6.

GUO Lili，LIU Jiaxin，LI Beiming.Research on Acquisi⁃tion Algorithm of Combinatory Pseudo-random Codes in Parallel Combinatory Spread Spectrum System［J］.Jour⁃nal of Telemetry，Tracking and Command，2014（3）：1-6.

Correlation Properties of Combinatory Gold-Walsh Sequences Analysis and Application in Spread Spectrum Communication

ZHANG Ye
（No.92124 Troops of PLA，Dalian116023）

According to the concept of correlation properties of combinatory sequences，the correlation function at zero time delay of combinatory Gold-Walsh sequence is analyzed，and the muti-peak values of correlation function at non-zero time delay is discussed.Aiming at the good correlation properties of combinatory Gold-Walsh sequences，simulation is built in asynchronous par⁃allel combinatory spread spectrum system.The results show that Gold-Walsh sequences self-synchronization of parallel combinato⁃ry spread spectrum system can be realized.

Gold-Walsh sequences，correlation properties，parallel combinatory spread spectrum system，sequences syn⁃chronization

TN914

10.3969/j.issn.1672-9722.2017.05.009

2016年11月21日，

2016年12月30日

张野，男，硕士研究生，工程师，研究方向：通信与信息系统、扩频通信等。