LEO太阳电池一次放电模型研究

全荣辉，池卫英，贾巍，方美华，黄三玻



LEO太阳电池一次放电模型研究

全荣辉1，池卫英2，贾巍2，方美华1，黄三玻2

（1. 南京航空航天大学，南京 210016；2. 上海空间电源研究所，上海 200040）

空间等离子体作用下,太阳电池一次放电是诱发二次放电的主要原因。目前缺乏适合工程应用的一次放电快速评估模型。文章借鉴辉光放电理论，针对太阳电池三联点结构提出一次放电一维简化模型，用于评估太阳电池设计对放电脉冲强弱的影响。模型计算结果表明，增加玻璃盖片厚度和电池串联间隙有助于提高一次放电起始电压，一次放电频率随着太阳电池偏压和表面二次电子发射系数增加而增大，放电电流随着太阳电池偏压和电池阵电容增加而增强。该模型计算结果与试验测试结果基本一致，且比其他模型计算过程简单，可以为太阳电池设计中一次放电现象快速评估提供参考。

一次放电；太阳电池；表面充电；气体放电；仿真分析

0 引言

空间等离子体与在轨航天器相互作用会使航天器表面材料带上一定负电位，即发生表面充电现象[1-2]。太阳电池表面玻璃盖片与附近导体互连片之间容易出现反向电位梯度，且随着航天器表面充电程度和电池偏压增加，两者间电位差不断加大。此时若两者间存在少量材料释放的中性气体分子，则容易形成击穿而放电，即一次放电[3]。玻璃盖片等绝缘材料的二次电子发射会加快一次放电过程，形成对间隙电场的正反馈，进而增加一次放电强度。一次放电一般脉冲持续时间较短，对太阳电池材料本身通常无较大危害，但一次放电产生的等离子体云容易扩散到太阳电池串间隙之间形成二次放电。二次放电的能量由太阳电池提供，可以持续较长时间直至烧毁太阳电池，造成航天器供电系统的永久性故障[4-5]。

从20世纪70年代发现航天器表面充电现象起，国内外对一次放电和二次放电现象已进行了大量的在轨和地面模拟试验[6-8]。遗憾的是，由于空间环境和太阳电池结构的复杂性，一次放电的机理仍未明确，通常认为三联点结构放电现象是其主要诱发机制。虽然已有较多的理论和模型对太阳电池一次放电现象进行分析，但多是定性或半定量分析模型，在工程应用中较难使用和评估[9]。随着航天任务的不断发展，高压太阳电池阵越来越多地应用，而且伴随着太阳电池偏压的增加，空间等离子体诱发的一次放电和二次放电现象将更加频繁，因此对太阳电池一次放电现象的快速准确评估已成为当前的迫切需求。

本文提出了一维简化模型，并通过试验数据验证了其在一次放电起始电压、放电频率和放电电流强度等方面的计算结果，旨在为太阳电池一次放电防护设计提供简单快速的评估。

1 模型的建立

1.1 气体放电机制

太阳电池三联点结构放电理论最早由Mengu Cho和Hastings等人提出[3]。太阳电池串联间隙内的导体互连片与盖片胶及玻璃盖片、电池间隙空间形成三联点，如图1所示。LEO太阳电池导体互连片偏压一般在-60V以上，而玻璃盖片表面充电电位（未穿越极区时）为-1V左右。此时导体互连片电位远低于玻璃盖片表面电位，形成反向电场梯度，为一次放电形成了基本条件。需要注意的是，导体互连片与玻璃盖片表面距离很小，因此该处的反向电场较强。

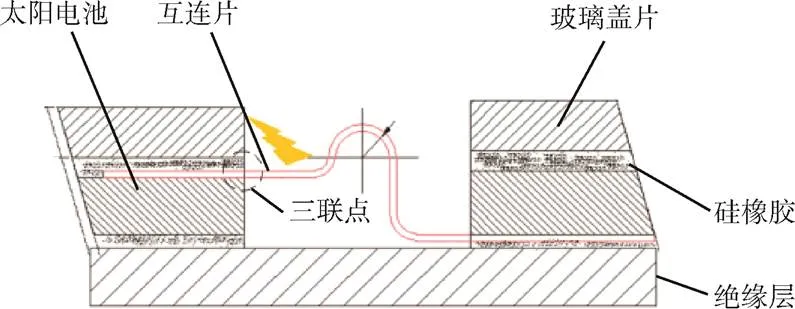
图1 三联点结构

一次放电基本过程如下：

1）在场致发射效应作用下，导体互连片不光滑边缘或毛刺区域开始向外不断发射电子。弯折处、互连片上的部分污染点或缺口点容易发生场致发射效应。

2）电子与间隙内材料放气产生的中性气体分子发生碰撞电离，产生更多的电子和离子。材料放气过程包括缓慢的渗透式放气和突发性的释放过程。材料渗透式放气在真空中迅速扩散漂移，无法对电子形成明显的倍增效应，因此一次放电多与突发性气体释放过程相关，这给一次放电现象的位置确定和强度评估带来困难。为便于计算分析，本模型中仅考虑已发生突发性放气情况。

3）电子以一定能量入射到盖片胶和玻璃盖片表面，促进中性气体分子释放，同时产生二次电子。

4）玻璃盖片表面通常镀有增透膜等材料，二次电子发射系数大于1。受到电子入射影响时，大量二次电子从玻璃盖片表面发射，造成玻璃盖片表面电位上升，进而增强了间隙内反向电场强度，形成正反馈现象。

5）该过程不断重复，放电强度逐渐增加，直至玻璃盖片表面电位上升至一定正电位，此时一次放电电流达到最大值；之后间隙内中性气体分子及表面充电电荷逐渐耗尽，一次放电电流下降至最小值。

6）空间等离子体对玻璃盖片等重新充电，恢复至初始电位分布情况。

在上述过程中，导体互连片的偏压达到一定值（即间隙内电场强度达到阈值）是一次放电发生的必要条件之一；在初始状态下，导体互连片场致发射电子电流十分微弱，间隙内中性气体或电场正反馈现象的存在是放电电流强度明显增加并形成可观测的一次放电现象的必要条件之二。玻璃盖片的二次电子发射对放电电流同样也有增强的作用。

1.2 模型的建立

根据上述放电过程，借鉴辉光放电理论，考虑电子与离子在间隙内的输运过程，其基本方程如下[10]：

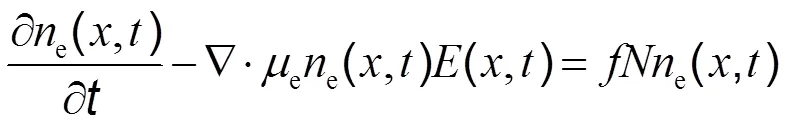
；(2)

； (3)

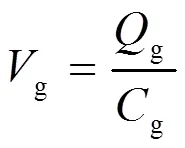
上述方程中，e(,)为间隙内电子数密度；e为电子迁移率；(,)为间隙电场；为电离产生率；为间隙内中性分子气体数密度；i(,)为离子数密度；i为离子迁移率；g为玻璃盖片表面电位；g为玻璃盖片表面电荷；g为玻璃盖片电容。

上述方程中未考虑电子、离子和中性分子的扩散运动。电离产生率与电子运动速度，中性气体碰撞截面相关，可以表示为

=e(,)≈e(,)。 (5)

考虑上述方程组的边界条件，在导体互连片的一侧，场致发射效应所引起的电子通量为[11]

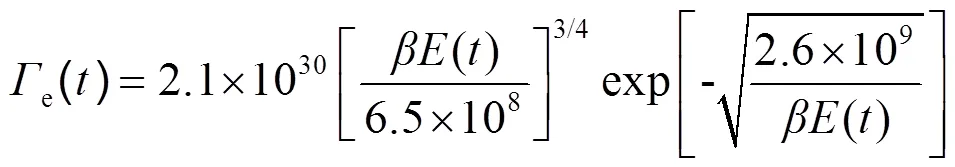
式中为形貌参数，取值范围根据材料平滑度通常在1～100之间，本文计算过程中取19。考虑到太阳电池电容s的影响，则在一次放电瞬间，由于场致电子发射引起的互连片电位变化为

dc=dc/s。 (7)

其中：c为导体电压；c为导体电量。

对于玻璃盖片，若不考虑电子在玻璃盖片侧面弹跳过程，则玻璃盖片表面电位V()变化近似为

g()/dg()(1-)/g。 (8)

式中：g()为玻璃盖片表面入射电子电流；为二次电子发射系数。间隙内等离子体密度过大时会形成对电场的屏蔽作用，考虑其德拜长度（单位m）为

当德拜长度远大于玻璃盖片表面到导体互连片的距离时，它们之间的电场强度可以近似为

， (10)

式(10)中近似为放电电弧距离，与玻璃盖片厚度、盖片胶厚度及电池间隙宽度相关。在简化条件下，电弧若从间隙中心引发，则可以近似为间隙宽度的一半加上玻璃盖片和盖片胶厚度。此时结合式(1)～式(10)，根据LEO环境参数和太阳电池结构参数，可以通过数值计算得到一次放电的模拟结果。

2 模拟结果分析

2.1 一次放电阈值电压

一次放电阈值电压受到太阳电池串联结构、组成材料、互连片偏压和空间等离子体密度等多个因素共同影响。采用上述模型，在保持其他参数不变的前提下，初步分析LEO太阳电池一次放电过程中玻璃盖片与盖片胶厚度的影响。模拟过程中采用的相关参数如表1所示。

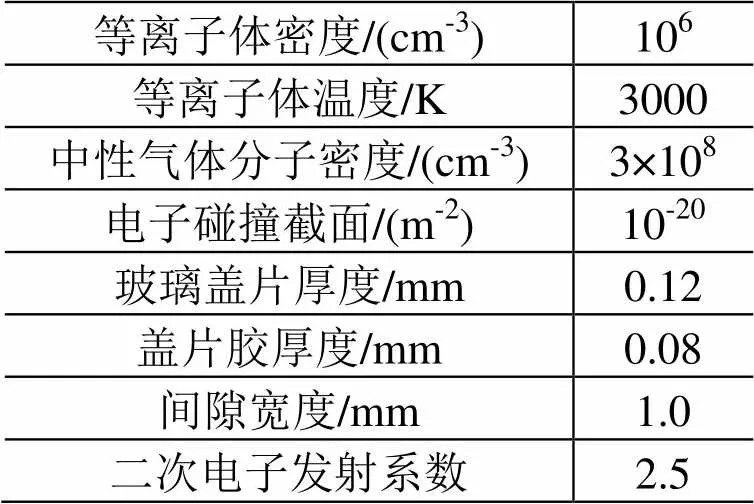
表1 计算中采用的等离子体与结构参数

由SPIS软件计算可知，在该参数条件下太阳电池的玻璃盖片表面充电电位在-0.5V左右。根据本文模型，可以得到太阳电池一次放电脉冲随电池偏压变化，如图2所示。由图2可见，一次放电脉冲强度随着互连片偏压增加而不断增强，而且随着偏压增加，脉冲上升时间迅速缩短。若取峰值电流强度0.1A为一次放电电流阈值，则在偏压达到-70V时，太阳电池开始发生一次放电现象，即临界电压为-70V，这与试验测量值是基本一致的[4]。

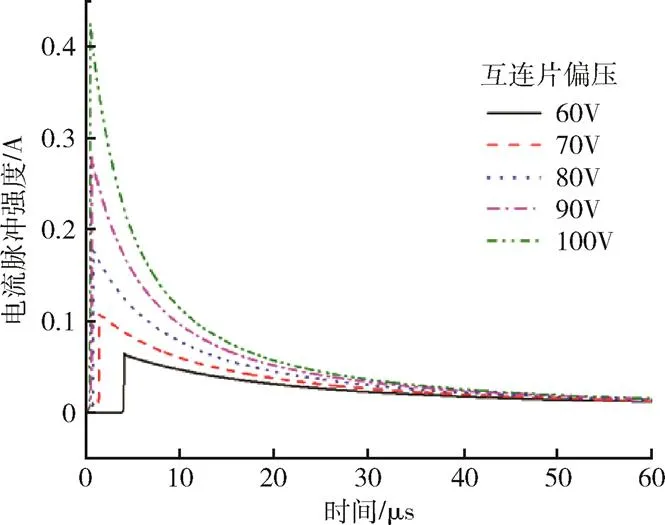
图2 一次放电脉冲随太阳电池偏压的变化

在太阳电池设计过程中，通过增加玻璃盖片和盖片胶厚度、加大间隙宽度、延长一次放电的电弧距离，可以提高一次放电临界电压。采用上述模型，通过增加太阳电池间隙宽度和增加玻璃盖片厚度计算得到一次放电阈值变化，如表2所示。

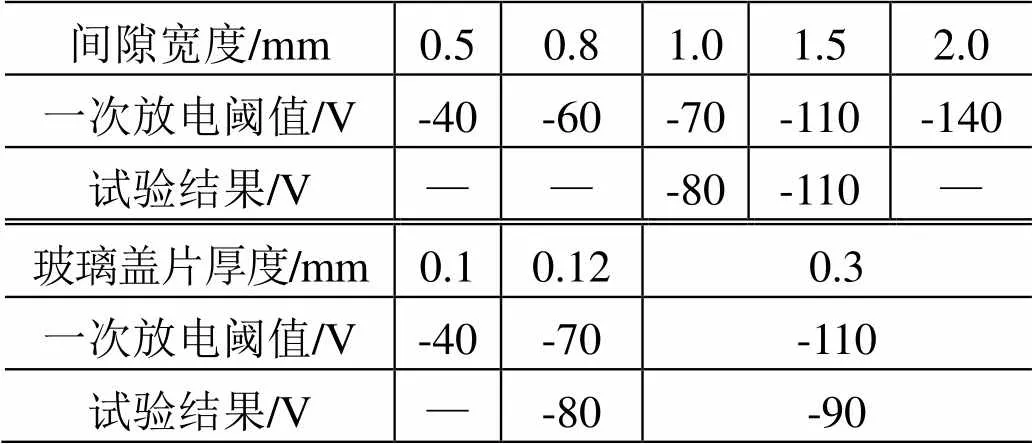
表2 不同结构条件下一次放电阈值

由表2可见，增加太阳电池间隙宽度，可以明显提高一次放电的阈值：不仅可以在一定概率上延长一次放电电弧长度，而且有利于降低间隙内中性气体分子密度。但间隙宽度增加，相同数量的太阳电池单元需要占更大的分布空间，不利于单位面积上太阳电池发电效率的提高，因此必须进行综合考虑。此外增加玻璃盖片厚度虽然也可在一定程度上提高一次放电阈值，但会降低透光率，不利于太阳电池发电效率的提高。

2.2 一次放电频率

LEO太阳电池的一次放电频率取决于以下几个方面因素：1）充电时间。由于LEO等离子体密度较高，航天器表面充电时间较短，一般为ms量级。2）材料放气在间隙内形成一定密度中性分子团的时间。由于该时间与粒子轰击及温度变化情况相关，目前尚无法准确判断。可以明确的是，该参数与材料放气率和中性气体扩散率密切相关。若放气时间较短，则需要材料在瞬时释放较多中性气体分子。3）放电脉冲的上升沿时间。该参数与太阳电池的结构、电池偏压、二次电子发射系数等均密切相关。结合模型分析太阳电池偏压和二次电子发射系数对上升沿时间的影响，得到计算结果，如图3和图4所示。

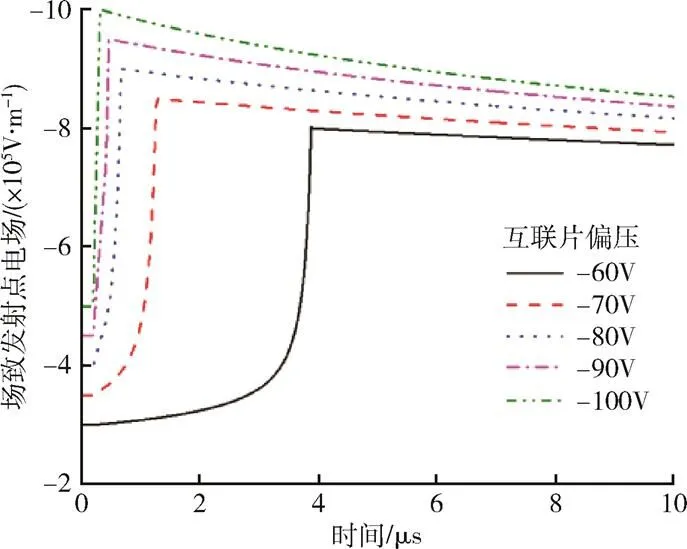
图3 不同偏压条件下场致发射点电场强度随时间变化

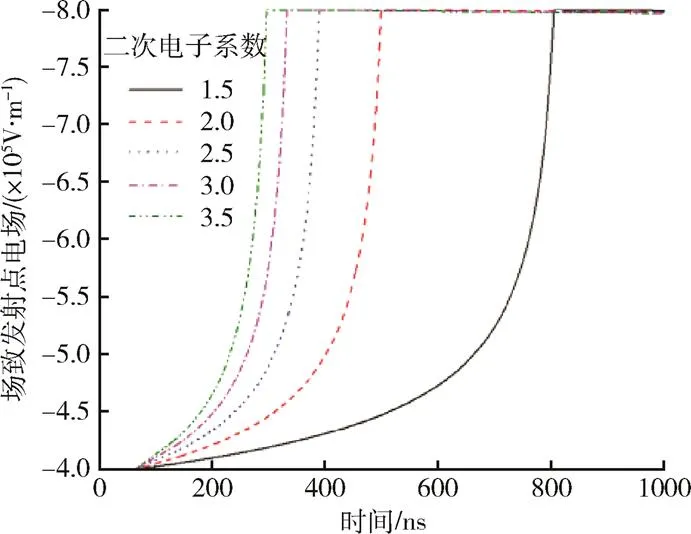
图4 场致发射点一次放电电场强度随二次电子发射系数变化（偏压-100V）

对比图3和图4可以发现，太阳电池偏压对一次放电脉冲上升沿时间的影响更为明显，例如当偏压为-60V时，脉冲上升沿时间为9.17μs；-100V时，为445ns，降低了1个量级。而且随着偏压增加，一次放电峰值电场强度迅速增加。相比之下，二次电子发射系数虽然也可以改变一次放电脉冲上升沿时间，但对最大电场强度无明显影响。同时由图4可见，二次电子发射系数对放电脉冲上升沿时间的影响随着系数增加而减少，在系数1.5附近较为明显。

根据PIX II地面和飞行试验的结果可知，太阳电池放电频率与偏压存在指数增长关系，而且在轨飞行期间可能由于原子氧和等离子体密度变化等原因导致其指数比地面试验值更高[12-13]。本论文模型未包含充电部分，因此无法准确评估其放电频率变化。此外，放电频率还与太阳电池的处理工艺，材料放气频率以及结构系数等密切相关，因此对于太阳电池放电频率的准确评估应该结合试验进行，同时对放电脉冲特征计算分析。

一次放电的频繁发生会显著增加二次放电概率。目前LEO在轨太阳电池通常都工作在-100V以下偏压；随着未来卫星功率需求增加，高压太阳电池阵是必然的选择，对于太阳电池设计也提出了更高的要求，太阳电池阵的结构和材料设计将面临较大的调整和变革。

2.3 一次放电强度

除了一次放电频率外，一次放电强度也是判断是否会引发二次放电的重要参数。高强度的一次放电，可以直接气化部分太阳电池材料，形成更为浓密的等离子体云，进而诱发二次放电。随着太阳电池偏压增加，放电脉冲宽度变窄，强度增强，即一次放电脉冲在单位时间内释放的能量更大，导致二次放电风险增加。此外，随着太阳电池电容增加，在相同的偏压条件下可具有更多可以释放的表面充电电荷，导致放电脉冲强度增加。结合一次放电模拟分析可以得到不同偏压和太阳电池电容条件下一次放电峰值电流分布（如图5所示）。

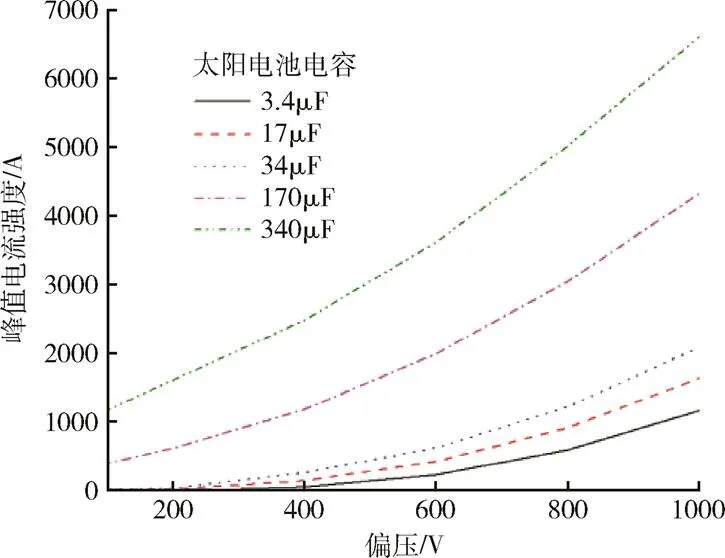
图5 不同电容条件下放电峰值电流随偏压变化

由图5可见，随着偏压增加至-1000V，放电峰值电流可以增加至1000A量级，而且随着太阳电池阵电容增加而迅速增大。高强度一次放电可以形成浓密的等离子体云，进而增加了二次放电风险。特别是太阳电池阵电容的增大，对于低偏压条件下一次放电强度有更为直接的影响。根据Synder和Miller等人试验结果，一次放电峰值强度与太阳电池阵电容存在0.994的指数关系[14-15]。因此在太阳电池阵表面放电防护设计中，必须注重太阳电池阵电容的影响，采取适当措施（如降低偏压等方式）减少一次放电频率，同时对互连片进行适当的绝缘防护等，避免出现较强的一次放电。

3 结束语

本文针对太阳电池一次放电现象，借鉴辉光放电理论，建立了一维简化模型，并采用该模型对一次放电起始电压、放电频率和放电强度等关键参数进行分析。模型计算结果表明：增加玻璃盖片厚度和串联间隙有利于提高一次放电阈值电压；一次放电频率与偏压密切相关；而放电峰值电流随着太阳电池电容增加而迅速增强。该模型计算结果与试验趋势基本一致，计算公式简单，具有一定工程应用价值，可以作为太阳电池防护设计的参考。

本文的模型未考虑中性气体扩散和衰减，以及充电过程的影响，采用碰撞系数作为电子电离过程近似，而作为完整的物理模型应当考虑上述因素。太阳电池一次放电和二次放电带有一定随机性，材料缺陷及处理工艺过程等各种非理想化因素均有一定程度的影响，因此完全的理论模拟是十分困难的。通过更好的物理近似和优化方法来完善本文模型，将是未来需要进行的工作。

（References）

[1] HILLARD G B. Plasma chamber testing of advanced photovoltaic solar array coupons[J]. Journal of Spacecraft and Rockets, 1994, 31(3): 530-532

[2] KENNERUD K L. High voltage solar array experiments: NASA-CR-121280[R], 1974

[3] CHO M, HASTINGS D E. Dielectric charging processes and arcing rates of high voltage solar arrays[J]. Journal of Spacecraft Rockets, 1991, 28: 698-706

[4] 黄建国, 刘国青, 姜利祥, 等. 高压太阳电池阵诱发的航天器充电及放电机理[J]. 中国科学: 地球科学, 2015, 45: 43-51

HUANG J G, LIU G Q, JIANG L X, et al. Mechanisms of spacecraft charging and discharging induced by high voltage solar arrays[J]. Science China: Earth Sciences, 2015, 45: 43-51

[5] GRIER N T. Plasma interaction experiment II: laboratory and flight results[C]∥Spacecraft Environment Interactions Technology Conference. Colorado, 1985: 333-348

[6] BERTHOU C, BOULANGER B, LEVY L. Plasma ESD qualification test procedure of alcatel alenia space solar array[J]. IEEE Transactions on Plasma Science, 2006, 34(5): 2004-2010

[7] TAKAYUKI O, YUYA S, TOMOKI K, et al. Emission spectral analysis of arc plasma on solar array in geo environment[C]∥International Symposium on Discharges and Electrical Insulation in Vacuum. Matsue, 2006: 750-753

[8] BAO H, FRANKIE K W, RONALD L C, et al. Combined space environmental exposure test of multijunction GaAs/Ge solar array coupons[J]. IEEE Transactions on Plasma Science, 2012, 40(2): 324-333

[9] FERGUSON D C. Space solar cell edge, interconnect, and coverglass designs and their effect on spacecraft charging and plasma interactions[C]∥Photovoltaic Specialists Conference (PVSC). Honolulu, Hawaii, 2010: 002537-002542

[10] PAI S T. Analytic approach to glow discharge theory: the physical model[J]. Journal of Applied Physics, 1992, 71(12): 5820-5825

[11] KOZYREV A V, KOZHEVNIKOV V Y, SEMENYUK N S. Theoretical simulation of a low pressure gas breakdown in the gap with combined metal-dielectric electrodes[C]∥XXVI International Symposium on Discharges and Electrical Insulation in Vacuum. Mumbai. India, 2014: 29-34

[12] FERGUSON D C. The voltage threshold for arcing for solar cells in LEO-flight and ground test results[C]//24thAIAA Aerospace Science Meeting. Reno, USA, 1986

[13] HASTINGS D E. A review of plasma interactions with spacecraft in low earth orbit[J]. Journal of Geophysical Research, 1995, 100(A8): 14457-14483

[14] SNYDER D B. Characteristics of arc currents on a negatively biased solar cell array in a plasma: NASA TM 83728[R], 1984

[15] MILLER W L. An investigation of arc discharging on negatively biased dielectric conductor samples in a plasma[C]∥Spacecraft Environmental Interactions Technology Conference. Colorado, 1985: 367-377

（编辑：冯露漪）

1D modelling of primary arcs on LEO solar array

QUAN Ronghui1, CHI Weiying2, JIA Wei2, FANG Meihua1, HUANG Sanbo2

(1. Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;2. Shanghai Institute of Space Power Sources, Shanghai 200040, China)

The primary arcs on the solar arrays are the main cause of secondary arcs, a serious threat to the safety of spacecraft operation. The primary arcs were widely studied but without a fast assessment model. A 1D model of the primary arcs is developed to explain the experimental results under different discharging conditions. Both effects of the electric field enhanced emission and the electron impact ionization are included by using an equivalent capacity model for the boundary condition. The primary arc characteristics under different conditions can be predicted. The effects of the differential surface potential, the cover glass thickness, and the secondary emission coefficient are studied. It is shown that the onset voltage of the primary arc grows with the increase of cover glass thickness and the solar cell gap distance, the discharging frequency is affected by the bias voltage and the secondary emission coefficient, and the peak current is proportional to the bias voltage and the solar array capacitance. The results are consistent with experiments and can provide a fast assessment of the primary arc in a solar array design.

primary arc; solar array; surface charging; gas discharging; simulation analysis

P354.2; V416.5

A

1673-1379(2017)02-0156-06

2016-11-23；

；2017-04-01

南京航空航天大学青年科技创新基金（编号：NS2014089）

全荣辉（1981—），男，博士学位，副教授，主要从事空间环境效应及应用研究。E-mail: quanrh@nuaa.edu.cn。

http://www.bisee.ac.cn

E-mail: htqhjgc@126.com

Tel: (010)68116407, 68116408, 68116544