基于自适应带通滤波的航天器正弦扫频试验数据处理方法

尹钊，侯向阳，郭军辉，高海洋



基于自适应带通滤波的航天器正弦扫频试验数据处理方法

尹钊1，侯向阳1，郭军辉1，高海洋2

（1. 中国空间技术研究院载人航天总体部；2. 北京卫星环境工程研究所：北京 100094）

为解决传统STFT（Short Time Fourier Transform）方法因非同步采样引起频谱泄漏，造成频域曲线幅值降低，产生较大误差的问题，提出一种基于频域带通滤波的数据处理方法，通过在频域逐次移动带通滤波器的中心频率，获得信号中各个频率分量幅值的最大值。利用该方法对某载人航天器搭载的力学参数测量系统在整器正弦振动试验中采集的数据进行频谱分析，结果表明，该方法可有效获取力学参数测量系统各测点的频率幅值曲线，减少传统STFT方法产生的能量泄漏的影响。研究成果也可用于不依赖振动控制仪或无COLA通道的数据采集系统正弦振动试验的数据处理。

航天器；正弦扫频；带通滤波；数据处理

0 引言

航天器正弦振动试验是一项重要试验，用以考核航天器结构适应振动环境的能力，暴露航天器制造的潜在缺陷，有助于提高航天器的在轨可靠性[1-2]。在试验中，通过将响应的时域数据变换为频域数据的处理，获得响应的频率与幅值关系曲线，这对于正弦振动试验的响应分析至关重要[3]。

对航天器正弦扫描振动响应数据的分析处理，目前主要采用具有COLA（Constant Output Level Adaptor）功能的数采系统[4-7]。振动控制仪输出等幅值的COLA信号，数采系统由此实现频率跟踪的实时辨识，然后处理每个实时频率点对应的信号幅值[8-9]。

载人航天器在发射段和交会对接期间经历较为复杂的载荷环境，因此，获取这些阶段的动力学响应数据尤为重要，可为载人航天器结构优化、寿命评估、以及后续载荷条件的制定与优化提供数据支持。而搭载在载人航天器上的力学参数测量系统由于无COLA功能需对其在振动试验中获取的响应数据进行处理，以形成有效的频域曲线，并与载人航天器振动试验相应的测点数据的一致性进行比较，从而验证力学参数测量系统的有效性。因此有必要对其正弦扫描试验数据的处理方法进行研究，从而得到准确的频率-幅值关系。

目前有学者提出了不使用COLA信号，而使用控制系统驱动信号的方法对数据作局部处理。文献[8]提出了基于Hilbert变换和跟踪滤波的正弦振动数据处理方法，该方法无须振动控制仪和数采系统的COLA通道，而是用同步采集振动测量设备的驱动信号作为参考信号，采用Hilbert 变换对航天器正弦扫描试验的时域信号进行时频分析和处理，能够得到较好的分析结果。但同步采集控制仪驱动信号将不可避免地引入直流信号，这些干扰信号被振动台的功放系统放大后，会影响试验控制[10]。因此该方法在应用上可能存在一定安全隐患。

此外，在不使用COLA信号的基础上，有学者更进一步提出了不依赖控制系统驱动信号的处理方法。文献[3]提出一种基于满足一定条件的正弦振动试验数据处理方法，该方法摈弃传统方法中利用驱动信号作为参考信号的手段；实例分析表明其计算结果精度较高，误差很小。但该方法必须满足参考信号的频率范围、扫描速率与响应信号相等以及采样频率相同的约束，且不能用于对非主振方向响应信号的处理，因此具有一定的局限性。

在现有的正弦扫描数据后处理方法中，FFT是较为常见的一种分析方法。FFT方法存在对信号的非整周期截断，会引起能量泄漏以及栅栏效应，导致从时域变换至频域后，频谱的幅值变小、测量精度降低等问题[11-25]。众多学者基于各类窗函数的加窗FFT方法提出了多种修正算法，使频率分析的精度得到了提高[26]，频谱泄漏在一定程度得到了抑制。但是这些方法大都存在一定的局限性，且加窗插值算法比较复杂。在对周期信号进行处理时应同步采样，保证对信号的整周期截断。但在航天器的振动试验中无法同步采样，因此非同步采样导致的频谱泄漏不可避免[17,27]。

为了分析正弦扫描信号中各频率分量的幅值变化规律，本文在FFT方法的基础上提出了自适应带通滤波器的短时傅里叶变换（STFT）方法，将STFT在时域加窗的思想应用在频域中。拟通过逐次移动带通滤波器的中心频率，获得信号中各个频率分量幅值的最大值，并利用该方法对某型号载人航天器搭载的力学参数测量系统所获取的正弦振动试验数据进行处理。

1 传统FFT方法

1.1 STFT方法的特点

在载人航天器的正弦振动试验过程中，扫描频率是随着时间不断变化的，因而结构响应中的频率成分也随时间不断变化，使得结构响应信号为非平稳信号[2]。STFT是一种常用的时频分析方法，它所采用的窗函数是固定不变的。由不确定性原理可知，时间分辨率与频率分辨率不能同时达到很高，想要提高频率分辨率就需要以牺牲部分时间分辨率作为代价。

1）对于频率不随时间变化的信号

计算机处理的数据为有限长度的数据，这相当于对原正弦或余弦信号乘以一个矩形窗的结果，在频域上表现为频谱泄漏，在其中心频率之外还有一些频率成分，从而使FFT所求的中心频率的幅值比时域曲线的幅值略小。

2）对于频率随时间变化的信号

在进行频域变换后只留下信号幅值随频率的变化信息，故可认为该信号中包含所有频率的正弦分量不随时间变化，因此对应某个时间段的正弦分量的幅值将在整个时间域中取平均，会带来幅值的下降。

1.2 STFT算法计算流程

采用STFT方法处理正弦扫描振动试验数据时，首先对试验数据进行采样，形成离散序列，然后对信号进行加窗，在每个周期内用傅里叶算法计算信号频率[28]，最终得到信号的幅值谱。具体分析过程如图1所示。

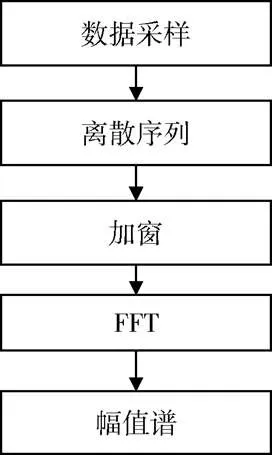
图1 STFT频谱分析过程

加窗能够降低非整周期采样等原因引起的频谱泄漏问题，但由于STFT每个小时间窗口内信号的变换只处理了部分数据，数据量较小，必然造成频域分析中对应幅值和功率谱线精度的下降。即在对信号进行频谱分析时，将原序列截断，必然造成截断效应。若采样频率为一个固定值，在用FFT方法时就会出现非整周期截断，频谱分布引起主瓣被旁瓣淹没的现象，造成频谱泄漏。

由于FFT运算时会对信号时域截断，原来集中的能量被分散到2个较宽的频带，即引起了频谱能量泄漏[16]。虽然通过改变窗函数的大小可以削弱泄漏问题，但任何窗函数都不能解决主瓣处偏离零值点而导致的误差，因此其对泄漏的减小也是有限的，必须寻求新的解决方法。

2 基于自适应带通滤波器的STFT方法

为了分析信号中各频率分量的幅值变化规律，将STFT在时域加窗的思想应用在频域中，提出基于自适应带通滤波器的STFT方法。自适应带通滤波器由多个带通滤波器并联组成，其主要思想是对信号进行逐级式频率分析，且这些带通滤波器的带宽能够覆盖整个信号所在的频带。首先对整体信号做FFT，获取全时间范围内各个频率分量的平均幅值。其次，采用频域加窗，即带通滤波器，对整个信号进行带通滤波，保留中心频带的信号并滤除中心频带之外的信号，获取中心频带信号的频率分量，统计该滤波信号的最大幅值。采用三分之一倍频程谱分析原理，各频率点处的幅值由一系列频率点和对应这些频率点附近频带内信号的最大幅值构成。将这些频率点定义为中心频率c，中心频率附近的频带在上限频率u和下限频率l之间。一般选取中心频率为1、1.25、1.6、2、2.5、3.15、4、5、6.3、8、10、……，即每间隔3个中心频率，频率增加一倍。中心频率与上、下限频率的关系如下：

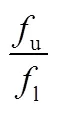
三分之一倍频程的带宽为

。 (2)

在信号频率分析范围内，逐次移动带通滤波器的中心频率，从而获得信号中各个频率分量幅值的最大值。

2.1 算法计算过程

基于自适应带通滤波器的STFT方法的流程图如图2所示。

图2 基于自适应带通滤波器的STFT算法计算流程图

Fig. 2 Process of STFT method based on band pass filter

算法计算流程如下：

1）首先定义三分之一倍频程的中心频率

如：cBasic0= [1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00]；

cBasic = [c_Basic0, 10*c_Basic0, 100*c_Basic0,

1000*c_Basic0, 10000*c_Basic0]。

其中：cBasic0为基准频率；c_Basic为三分之一倍频程的中心频率。

2）计算中心频率与下限频率比值ratio。

3）取中心频率总的长度为Num_c，采样信号长度为，即Numclength(c);length(Signal)；其中Signal为采样信号。

4）FFT

_FFT = fft(Signal, NFFT)，

其中NFFT为FFT的点数。

5）计算信号的三分之一倍频程Oct13SP2，中心频率为cRange信号的均方根值为

Oct1_3SP2 = nan(Numc, 1)。

6）计算下限频率和上限频率为

_low =c(Sn_c)/_ratio，

_up =c(Sn_c)´_ratio。

7）频域加窗，以每个中心频率段为通带进行带通频域滤波，即

BankPassFilter_Spectrum = zeros(1, NFFT)；

BankPassFilter_Spectrum(Index_InRange) = Signal_FFT(Index_InRange)；

BankPassFilter_Spectrum = fftshift(BankPassFilter_Spectrum)。

8）对频域信号进行IFFT，即

Signal_BankPass = IFFT(BankPassFilter_Spectrum, NFFT)。

9）计算对应每个中心频率段的最大值为

Oct1_3SP2(Sn_c) = max(Signal_BankPass)。

10）在频域逐次移动带通滤波器的中心频率，得到各频率分量最大值为

c3_1Oct =c(1:Num_c)；

Oct1_3SP2 = Oct1_3SP2(1:Num_c)。

2.2 算法应用算例

利用该算法对给定的单自由度系统扫频信号进行响应分析。扫频信号时域曲线如图3所示。频域曲线理论值如图4所示。基于自适应滤波方法及FFT方法的频域曲线分别如图5和图6所示。算例分析结果见表1。

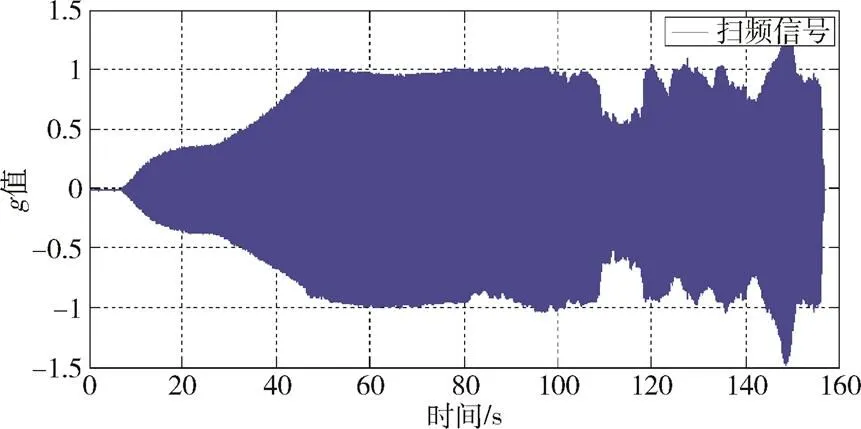
图3 扫频信号时域图

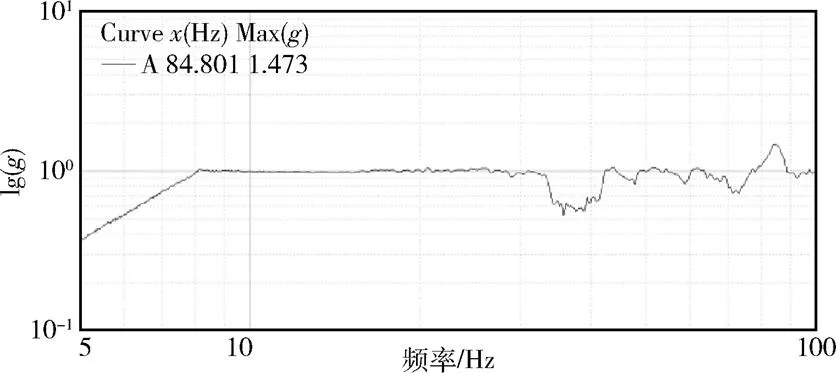
图4 扫频信号频域曲线（理论值）

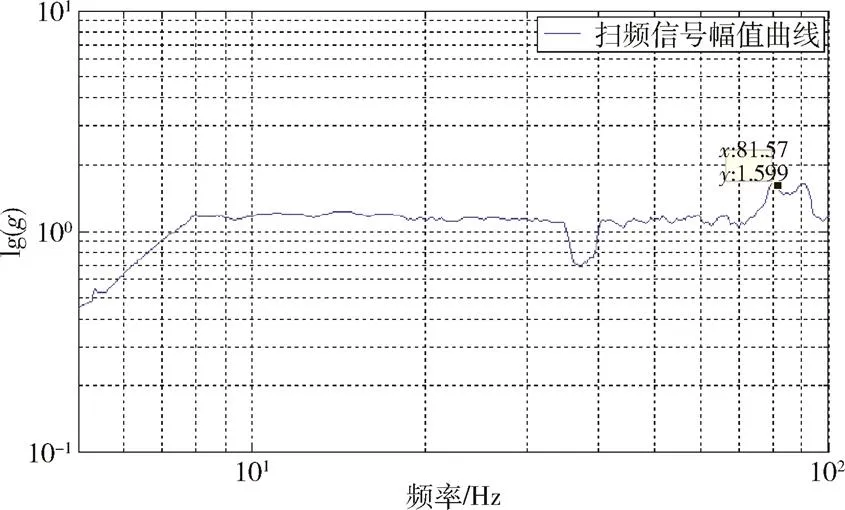
图5 扫频信号频域曲线（基于自适应滤波算法）

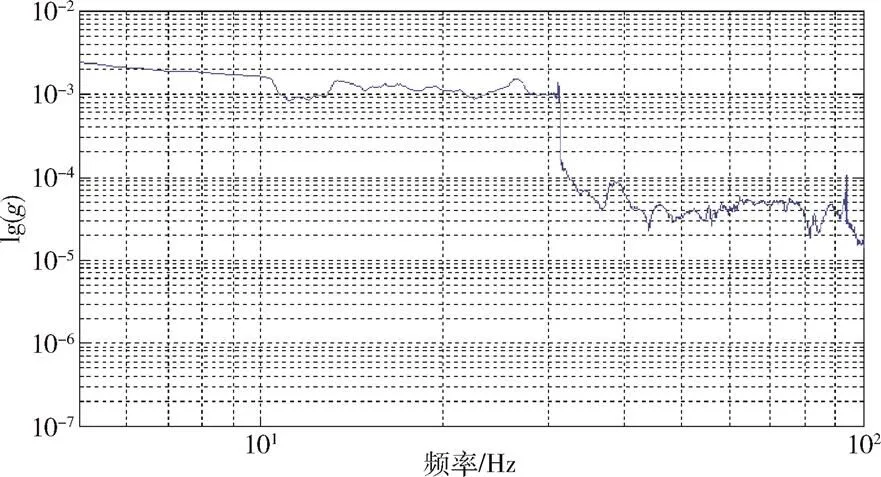
图6 扫频信号频域曲线（基于传统FFT算法）

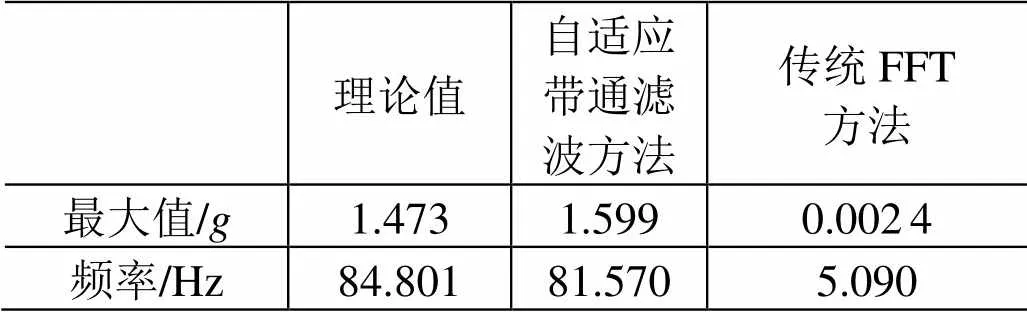
表1 算例分析结果

通过计算2种方法与理论值的相关性，得到自适应带通滤波方法与理论值的相关系数为0.99855，为极强相关，较好地反映了扫频信号幅值随频率的变化关系。而FFT方法由于存在频谱泄漏，处理结果与理论值差距较大。仿真与试验分析表明，自适应带通滤波方法可以较好地获取信号中各频率分量的幅值随频率的变化规律。

3 振动试验及结果分析

3.1 试验工况

本文对某型号航天器平台与其搭载的力学参数测量系统获取的振动试验数据进行分析。振动试验中，整器平台测点由具有COLA功能的数据采集系统负责采样，并将获取的数据处理成频域曲线；振动控制仪能够输出幅值相同的COLA信号；地面数采系统能够实时辨识信号频率，并处理每个频率点对应的信号幅值[8]；由采编单元负责采集搭载系统测点的振动响应数据，其目的之一是与平台测点滤波后数据进行比较，验证搭载力学参数测量系统数据获取的有效性，因此搭载系统的传感器安装在平台测点传感器附近。平台测点与搭载系统测点如表2所示。振动试验方向依次为向、向、向，选取每个方向试验中的主振方向作为测量方向进行数据比对分析。

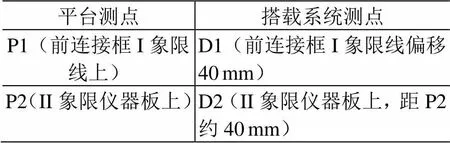
表2 平台测点与搭载系统测点的位置及对应关系

3.2 试验条件

以正弦扫描振动试验中验收级试验数据为例进行数据处理，试验条件见表3所示，其中：为扫描频率；为扫描的基频；为单位时间内扫描的倍频程增量；为扫描时间。

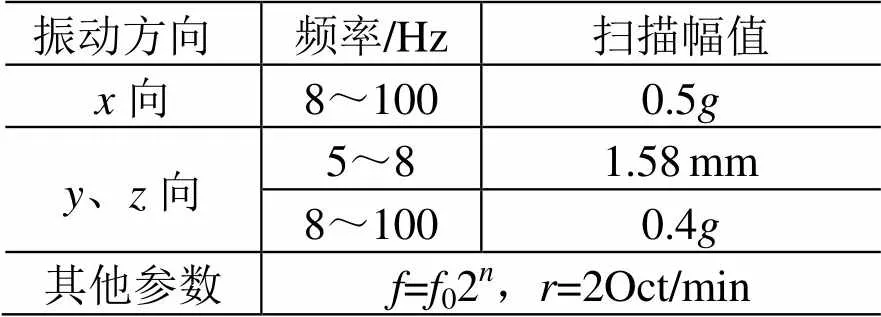
表3 正弦扫描振动试验条件(0～P峰值)

3.3 试验结果分析

首先将载人航天器平台测点所获取的数据利用正弦扫描振动试验的数据采集系统处理成频域曲线；其次，采用STFT方法处理载人航天器平台测点与搭载系统测点数据；最后利用本文提出的自适应带通滤波器的方法分别将载人航天器平台测点滤波后数据及搭载系统测点数据处理成频域曲线，通过不同方法处理结果以及数据的相关性分析，评价对所获取的原始数据在扫描频带范围内进行滤波后且采用基于自适应滤波处理方法进行数据频域处理的有效性。

3.3.1 振动试验数据采集系统的处理结果

图7和图8是将载人航天器平台测点所获取的数据滤波后利用正弦扫描振动试验中地面数据采集系统处理成频域曲线。从图7和图8可以看出，扫描频率从5Hz变化至100Hz过程中，平台测点P1的最大响应出现在10.414Hz处，幅值为1.109。平台测点P2的最大响应出现在74.063Hz处，幅值为1.181。

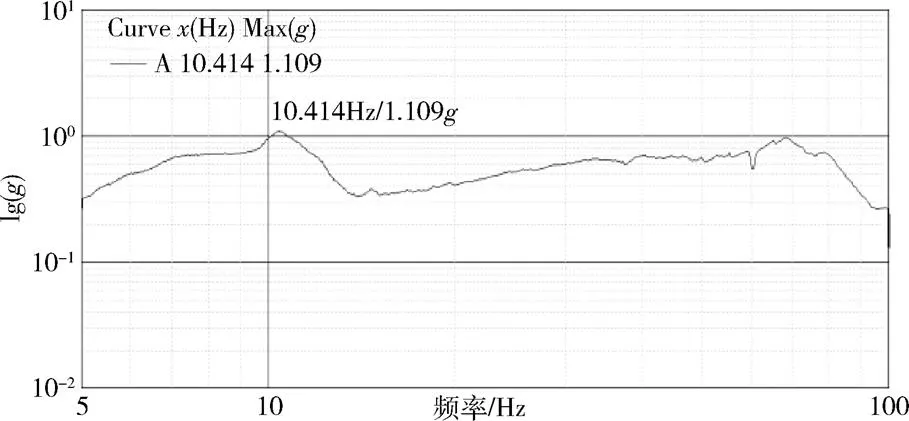
图7 地面数采系统处理的平台测点P1频域曲线（z向）

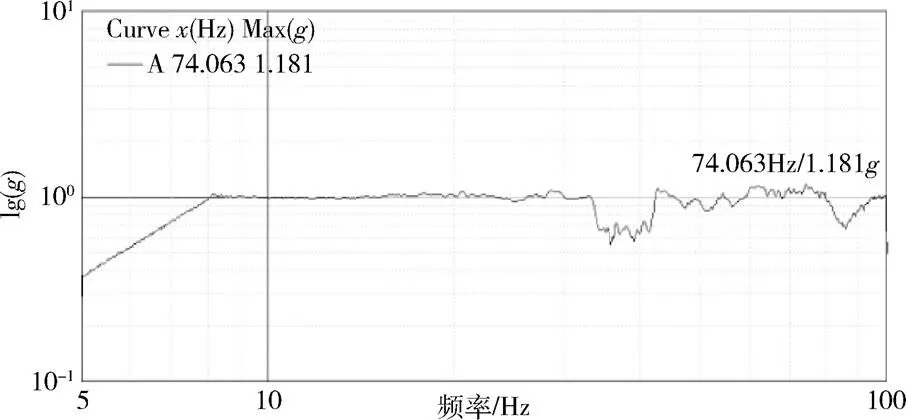
图8 地面数采系统处理的平台测点P2频域曲线（x向）

3.3.2 基于STFT方法的处理结果

采用STFT方法对平台测点P1、P2与搭载系统测点D1、D2数据进行处理，得到频域曲线，如图9和图10所示，从图中可以看出，STFT方法形成的频谱的幅值有较大幅度的下降，能量分散现象严重。

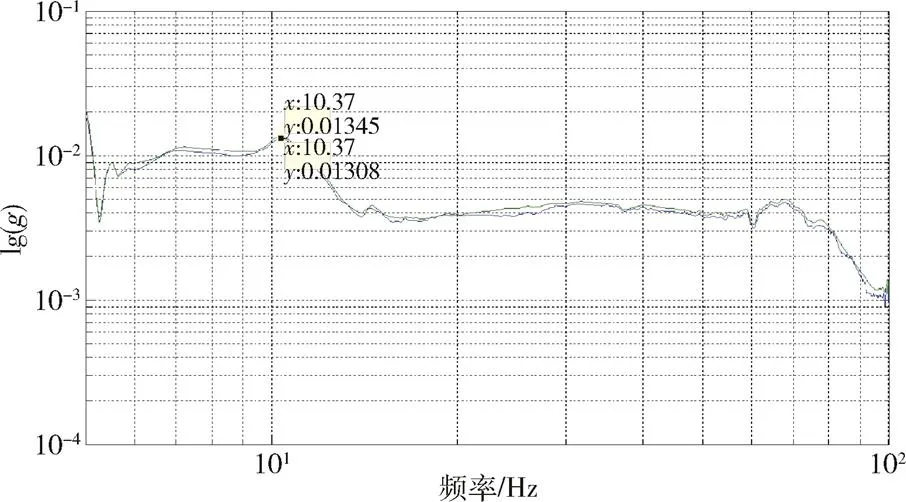
图9 基于STFT方法的平台测点P1与搭载系统测点 D1频域曲线（z向）

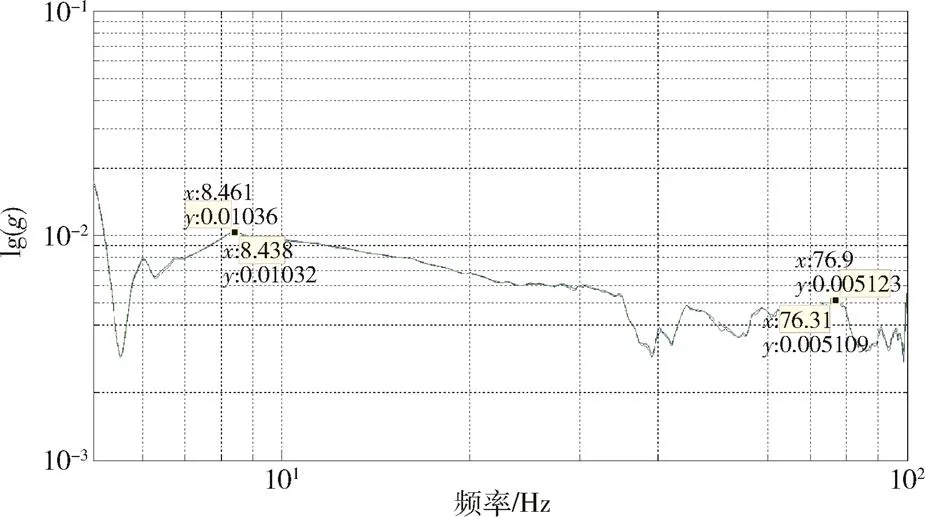
图10 基于STFT方法的平台测点P2与搭载系统测点 D2频域曲线（x向）

3.3.3 基于自适应带通滤波器的STFT方法的处理 结果

采用自适应带通滤波方法分别对向、向试验中整器平台测点P1、P2与搭载系统测点D1、D2的向、向的试验数据进行分析，求得振动试验中的最大加速度幅值及对应的频率，并与地面数采系统控制仪分析的结果进行比对，结果见表4。选取中心频率与下限频率的比值ratio=，FFT点数为2048，对信号进行FFT变换，下限频率选取为119.428Hz，上限频率为137.187Hz。对频域加窗，以每个中心频率段为通带进行带通频域滤波，此后对频域信号进行IFFT，计算对应每个中心频率段的最大值，逐次移动带通滤波器的中心频率得到各频率分量最大值。

图11和图12是基于自适应带通滤波器的STFT方法的平台测点与搭载系统测点的处理结果，可以看出，利用该方法处理得到的频域曲线，平台测点P1的最大响应出现在10.56Hz，幅值为1.174；搭载系统测点D1的最大响应也出现在10.56Hz，幅值为1.18。

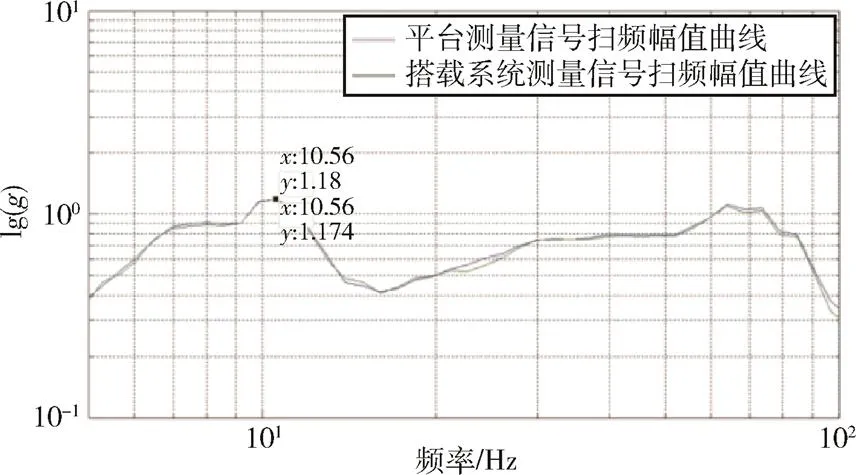
图11 基于自适应带通滤波器的STFT方法的平台测点P1与搭载系统测点D1频域曲线（z向）

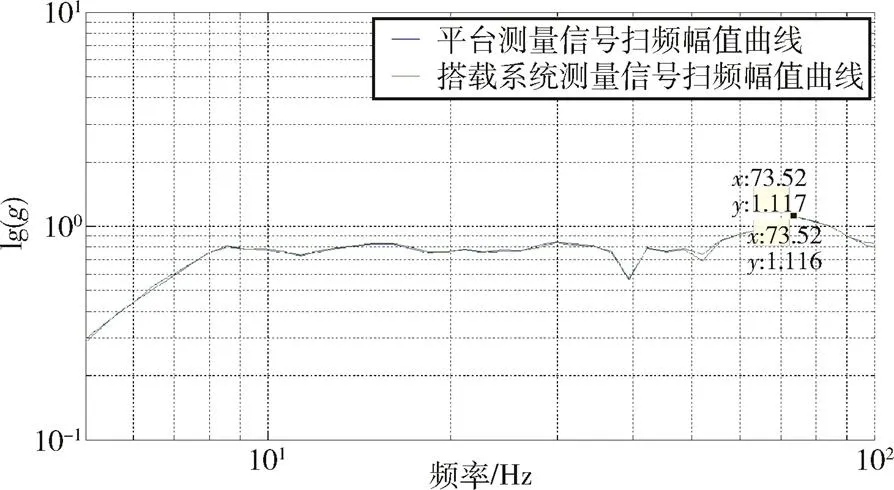
图12 基于自适应带通滤波器的STFT方法的平台测点P2与搭载系统测点D2频域曲线（x向）

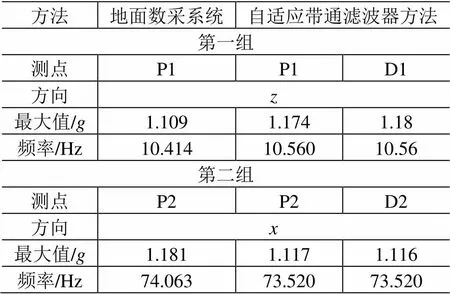
表4 试验数据对比

表5是对平台测点P1、P2分别采用自适应带通滤波方法处理结果与地面数采系统处理结果的数据（在扫描频带范围内进行滤波后）相关性分析，可以看出，采用本文提出的自适应带通滤波方法处理结果与地面数采系统处理结果的相关系数均在0.98以上，相关度均为极强。图11和图12中的频域曲线变化趋势是一致的，二者峰值及其对应的频率较为接近。基于自适应带通滤波方法较好地减小了由于信号截断引起的频谱泄漏带来的误差，处理结果接近于地面数采系统处理结果。

需要指出的是，由于搭载系统的传感器与平台测点安装位置不完全一致，故搭载系统测点与平台测点测得的最大加速度值和频率存在一定偏差，结果在合理范围内。

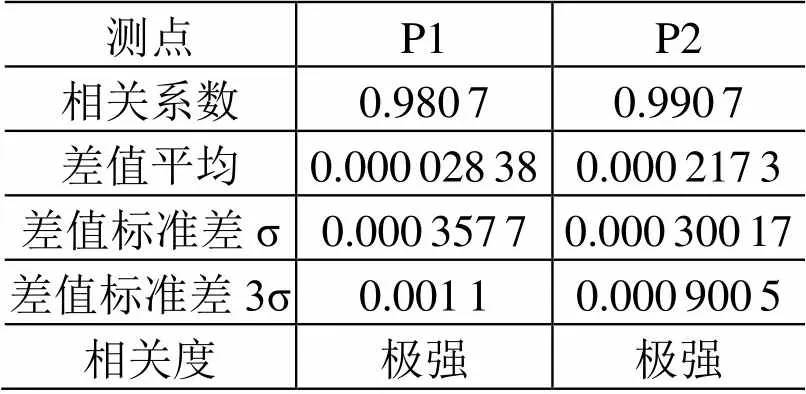
表5 地面数采系统与自适应滤波方法频域数据相关性 分析结果

4 结论

本文为解决载人航天器无COLA功能力学参数测量系统正弦振动试验数据处理方法，提出了一种基于自适应带通滤波器的STFT数据处理方法，通过试验验证与分析，得到以下结论：

1）该方法与地面数据采集系统对试验数据（滤波后）的处理结果相关性极强，频域曲线最大幅值及对应的频率较为接近，频域曲线变化趋势一致，能够有效减少STFT方法带来的频谱泄漏问题，改善幅值测试的精度，降低非同步采样对数据处理结果的影响。

2）该方法可用于对无COLA功能的数据采集系统地面正弦振动试验数据处理，并可对载人航天器搭载的力学参数测量系统在发射上升段与在轨期间获取的振动响应数据的处理提供参考价值。

3）基于自适应带通滤波方法可处理正弦振动试验中确定扫频范围的激励本身所产生的振动响应，并不包含由于航天器内部产生的其他振动信号，如舱内敲击信号。因此在与采用COLA功能的数据采集系统进行数据比对时，应将原始信号在扫频范围内进行滤波处理。

（References）

[1] 金恂叔. 航天器动力学环境试验的发展概况和趋势[J]. 航天器环境工程, 2003, 20(2): 15-21

JIN X S. The development status and trends of spacecraft dynamic environment testing[J]. Spacecraft Environment Engineering, 2003, 20(2): 15-21

[2] 田光明, 陈光礻禹. 正弦扫描振动响应的时频分析[J]. 振动与冲击, 2005, 24(6): 13-17

TIAN G M, CHEN G J. Time-frequency analysis of the response in a sine-swept vibration test[J]. Journal of Vibration and Shock, 2005, 24(6): 13-17

[3] 陈立伟, 孙立明, 杨博. 正弦扫描振动试验数据后处理方法研究[J]. 强度与环境, 2015, 42(4): 59-64

CHEN L W, SUN L M, YANG B. Research on post-processing of acquiring signals for sine swept vibration test[J]. Structure & Environment Engineering, 2015, 42(4): 59-64

[4] YANG Z D, CONG D C, HAN J W. Signal synthesis and analysis for swept-sine vibration control[J]. Journal of Vibration Engineering, 2008, 21(3): 309-313

[5] TONY K, UNDERWOOD M A. On acquiring and analyzing satellite sine vibration test data[C]//Conference Proceedings of the Society for Experimental Mechanics Series. IMAC-XXV-Celebrating 25 years of IMAC, 2007

[6] 韩晓健, 王睿. 应变测量中干扰数据的分析及处理[J]. 航天器环境工程, 2008, 25(5): 459-462

HAN X J, WANG R. Analysis and processing of noise data in strain measurement[J]. Spacecraft Environment Engineering, 2008, 25(5): 459-462

[7] 沈凤霞. 振动环境试验力参数测量技术研究[J]. 强度与环境, 2009, 36(5): 47-55

SHEN F X. Study on the measurement of force parameters in vibration test[J]. Structure & Environment Engineering, 2009, 36(5): 47-55

[8] 贺智国, 赵威, 骞永博. 基于Hilbert 变换和跟踪滤波的正弦扫描数据处理方法研究[J]. 强度与环境, 2012, 39(4): 40-45

HE Z G, ZHAO W, QIAN Y B. Research on processing of sine swept test signal based on Hilbert transform and tracking filter[J]. Structure & Environment Engineering, 2012, 39(4): 40-45

[9] 马阳阳, 李京华, 张燕荣. 基于FFT幅度和相位插值的频率估计改进算法[J]. 计算机与数字工程, 2012, 40(8): 39-41

MA Y Y, LI J H, ZHANG Y R. An improved frequency estimation algorithm based on FFT phase and amplitude[J]. Computer＆Digital Engineering, 2012, 40(8): 39-41

[10] 余小明, 高非, 徐兰菊, 等. 影响大型振动试验控制精度因素的探讨[C]∥2006 年度结构强度与环境工程专委会与航天空间环境工程信息网学术研讨会. 成都, 2006: 176-179

[11] 商一奇, 曹亦庆, 柴艳丽, 等. 振动信号的幅值和相位计算方法分析[J]. 计量、测试与校准, 2010, 30(4): 30-32

SHANG Y Q, CAO Y Q, CHAI Y L, et al. Analysis of amplitude and phase calculation methods of vibration signal[J]. Metrology & Measurement Technology, 2010, 30(4): 30-32

[12] 张强, 张频, 张明童. 加三角窗的频谱校正[J]. 振动与冲击, 2009, 28(2): 96-98

ZHANG Q, ZHANG P, ZHANG M T. Spectrum correction with a triangular window[J]. Journal of Vibration and Shock, 2009, 28(2): 96-98

[13] 孙晓华. 振动信号同步采集与频谱校正方法的研究[D]. 南京: 东南大学, 2011

[14] 李杭生, 陈丹. 频谱分析中窗函数的研究[J]. 微计算机信息, 2008, 24(4): 272-273

LI H S, CHEN D. Research of the window functions in frequency analysis[J]. Microcomputer Information, 2008, 24(4): 272-273

[15] 谭维凤, 冯立强, 王兵. 解决频域干扰处理法能量泄露问题的方法研究[J]. 通信技术, 2010, 43(12): 44-50

TAN W F, FENG L Q, WANG B. Solution of spectrum energy interference excision leakage in frequency domain algorithm based on FFT[J]. Communications Technology, 2010, 43(12): 44-50

[16] 李保环. 振动检测仪中自由衰减振动信号频谱校正的研究[D], 重庆: 重庆大学, 2010

[17] 陶薇薇, 张建秋, 陆起涌. 非同步采样信号频谱插值校正分析法[J]. 复旦大学学报, 2008, 47(6): 703-708

TAO W W, ZHANG J Q, LU Q Y. Spectral interpolated compensation analysis of non-coherent sampling signals[J]. Joumal of Fudan University, 2008, 47(6): 703-708

[18] 严天峰, 李强, 韩冬. 频谱监测中的谱泄漏及其抑制方法研究[J]. 计算机工程与设计, 2009, 30(7): 1790-1792

YAN T F, LI Q, HAN D. Method for leakage restraint in spectrum supervisal[J]. Computer Engineering and Design, 2009, 30(7): 1790-1792

[19] 马仁政, 陈明凯. 减少频谱泄漏的一种自适应采样算法[J] .电力系统自动化, 2002, 26(7): 55-58

MA R Z, CHEN M K. An adaptive sampling algorithm for reducing spectrum leakage[J]. Automation of Electric Power Systems, 2002, 26(7): 55-58

[20] 温和, 滕召胜, 王永, 等. 频谱泄漏抑制与改进介损角测量算法研究[J]. 仪器仪表学报, 2011, 32(9): 2087-2094

WEN H, TENG Z S, WANG Y, et al. Study on spectral leakage suppression and improved dielectric loss angle measurement method[J]. Chinese Journal of Science Instrument, 2011, 32(9): 2087-2094

[21] 潘立冬, 王飞. 一种减小频谱泄漏的采样频率自适应算法仿真研究[J]. 华北电力大学学报, 2005, 32(6): 5-8

PAN L D, WANG F. Simulation of software sampling frequency adaptive algorithm for reducing spectrum leakage[J]. Journal of North China Electric Power University, 2005, 32(6): 5-8

[22] 张鹏飞, 胡亚冰, 付玮, 等. 单帧FFT法在正弦扫描结构动特性试验数据处理中的应用[J]. 强度与环境, 2015, 42(2): 57-63

ZHANG P F, HU Y B, FU W, et al. Application of single frame FFT method in processing of sine swept structure dynamics test signal[J]. Structure & Environment Engineering, 2015, 42(2): 57-63

[23] 季冰, 梁志瑞, 牛胜锁. 基于最小旁瓣九项余弦组合窗的FFT谐波分析[J]. 电力科学与工程, 2012, 28(10): 16-21

JI B, LIANG Z R, NIU S S. FFT harmonic analysis based on nine terms minimum side-lobe cosine-sum window[J]. Electric Power Science and Engineering, 2012, 28(10): 16-21

[24] 齐国清. 几种基于FFT的频率估计方法精度分析[J]. 振动工程学报, 2006, 19(1): 86-92

QI G Q. Accuracy analysis and comparison of some FFT-based frequency estimators[J]. Journal of Vibration Engineering, 2006, 19(1): 86-92

[25] 齐国清, 贾欣乐. 插值FFT 估计正弦信号频率的精度分析[J]. 电子学报, 2004, 32(4): 625-629

QI G Q, JIA X L. Accuracy analysis of frequency estimation of sinusoid based on interpolated FFT[J]. Acta Electronic Sinica, 2004, 32(4): 625-629

[26] 刘广臣, 张惠安, 贾爱宾. 数字信号处理中的加窗问题研究[J]. 长沙大学学报, 2003, 17(4): 59-62

LIU G C, ZHANG H A, JIA A B. Study on the window-adding problem in the digital signal processing[J]. Journal of Changsha University, 2003, 17(4): 59-62

[27] 高云鹏, 滕召胜, 温和. 基于Kaiser窗相位差校正的电力谐波分析与应用[J]. 仪器仪表学报, 2009, 30(4): 767-773

GAO Y P, TENG Z S, WEN H. HarmoIlic analysis based on Kaiser window phase difference correction and its application[J]. Chinese Journal of Science Instrument, 2009, 30(4): 767-773

[28] 尹钊, 侯旭涛. 载人航天器在轨力学环境测量系统试验研究[J]. 航天器环境工程, 2016, 33(1): 95-99

YIN Z, HOU X T. Experimental study of orbital environment measurement system for manned spacecraft[J]. Spacecraft Environment Engineering, 2016, 33(1): 95-99

（编辑：闫德葵）

Data processing method in sine swept test for spacecraft based on adaptive band-pass filter

YIN Zhao1, HOU Xiangyang1, GUO Junhui1, GAO Haiyang2

(1. Institute of Manned Space System Engineering, China Academy of Space Technology;2. Beijing Institute of Spacecraft Environment Engineering: Beijing 100094, China)

The signal processing commonly relies on the vibration controller or the COLA (constant output level adaptor) data acquisition system in the sine vibration test for the manned spacecraft. For the mechanical parameter measurement system without the COLA function for the manned spacecraft, the traditional STFT(short time Fourier transform) method can result in a spectrum leakage due to the asynchronous sampling, thus the amplitude of frequency domain might be reduced and a major error might be produced. To solve the above problem, a data processing method based on the band pass filter in the frequency domain is proposed. The maximal values of the frequency components of the signal can be acquired by moving the center frequency of the band pass filter, and the spectrum analysis of the mechanical parameter measurement system in the sine vibration test for the manned spacecraft is acquired by the proposed method. It is shown that the proposed method can effectively acquire the spectrum at each measuring point of the mechanical parameter measurement system and the influence of the spectrum leakage by the traditional STFT method can be reduced. The research findings provide a reference for the signal processing method of the sine vibration test for the data sampling system independent of the vibration controller and without the COLA data acquisition system.

spacecrafts; sine swept; band pass filter; data processing

V416.2

A

1673-1379(2017)02-0214-08

10.3969/j.issn.1673-1379.2017.02.018

2016-09-02;

2017-03-16

国家重大科技专项工程

尹钊（1986—），男，硕士学位，主要从事载人航天器总体设计工作。E-mail: yinzhao08@126.com。

http://www.bisee.ac.cn

E-mail: htqhjgc@126.com

Tel: (010)68116407, 68116408, 68116544