基于大数据的配电网谐波经济损失评估方法研究
戴超凡, 邓孝祥, 蒋 煜, 丁晓群, 邓吉祥
(1.黑龙江科技大学 电气与控制工程学院, 黑龙江 哈尔滨 150022;2.河海大学 能源与电气学院, 江苏 南京 211100; 3.江苏省电力公司 泰州供电公司, 江苏 泰州 225300)
基于大数据的配电网谐波经济损失评估方法研究
戴超凡1, 邓孝祥1, 蒋 煜2, 丁晓群2, 邓吉祥3
(1.黑龙江科技大学 电气与控制工程学院, 黑龙江 哈尔滨 150022;2.河海大学 能源与电气学院, 江苏 南京 211100; 3.江苏省电力公司 泰州供电公司, 江苏 泰州 225300)
为了解决目前配电网谐波经济损失评估缺乏统一、科学的评估体系的问题,以电力大数据平台为基础支撑,建立了包含数据层、指标层和应用层的配电网谐波经济损失评估体系总体架构,构建了谐波经济损失评估指标体系.对常规粒子群算法进行改进,并和径向基(RBF)神经网络结合,利用混沌自适应粒子群优化的RBF(CAPSO-RBF)神经网络进行谐波网损评估.将Simoni模型与交联聚乙烯(XLPE)电缆谐波线芯温升模型结合,得到了谐波影响下的XLPE电缆绝缘老化寿命评估模型.案例分析证明了方法的可行性,验证了评估体系的合理性和电力大数据的优势.
大数据; 配电网; 谐波经济损失
近年来,随着生活中电力电子等非线性负荷的增多,一些高电压、大容量的非线性用电设备接入电网,在电网中产生了大量的谐波,电网受谐波污染的问题越来越严重.大量的谐波电流在配电网中流通,不仅使电网产生附加损耗,造成电能浪费,还会引起电力设备温度升高,加快绝缘老化,缩短设备的使用寿命.另外,谐波电流还会降低供电设备容量的利用率、增加设备故障率等.
目前,国内外对谐波的研究绝大多数集中在谐波的监测分析、抑制治理等方面.对配电网侧谐波经济损失评估研究较少,更多的是关于谐波对各电力设备损耗影响的研究,部分文献也给出了谐波对电力设备寿命影响的简化公式[1],但在谐波危害的经济量化方面评述较少[2],并缺乏统一的配电网谐波经济损失评估体系.在变压器方面,目前大多数文献都集中在对谐波影响下的变压器损耗[3-4]、发热问题[5-6]的研究.在电缆方面,大多数文献集中在对谐波影响下的电力电缆线路损耗进行研究[7-8],对谐波影响下的交联聚乙烯(Crosslinked Polyethylene,XLPE)电缆绝缘老化寿命经济损失的研究较少.在配电网方面,关于配电网的谐波网损计算,目前应用较多的方法是等值电阻法以及谐波电流总畸变率法[9-10].
本文针对配电网谐波经济损失评估缺乏科学、系统性研究的问题,以大数据平台为基础支撑,建立了配电网谐波经济损失评估体系.针对传统谐波网损计算繁琐、有误差等弊端,利用改进后得到的混沌自适应粒子群优化的径向基(Chaotic Adaptive Particle Swarm Optimization-Radial Basis Function,CAPSO-RBF)神经网络算法进行谐波网损评估.在XLPE电缆方面,通过Simoni模型建立了热-电协同作用下的XLPE电缆老化寿命模型,并结合电缆谐波线芯温升模型,建立了谐波影响下的XLPE电缆绝缘老化寿命模型.
1 评估体系总体架构和评估指标体系
考虑到配电网谐波经济损失评估涉及面广、需要的信息量大等特点,结合大数据技术在电力领域的应用现状,建立了以大数据平台为基础支撑的配电网谐波经济评估体系总体架构,主要分为数据层、指标层和应用层3层,如图1所示.
数据层以大数据平台为基础支撑,是经济损失评估的基础.通过从能量管理系统(Energy Management System,EMS)、停电管理系统(Outage Management System,OMS)、监视控制和数据采集系统(Supervisory Control and Data Acquisition,SCADA),以及各种智能电表、传感器等设备中获得数据,构建统一的电力大数据平台,利用大数据的数据整合、存储和处理等关键技术,为指标层各评估指标提供全面、准确的数据支撑,保证目标数据的精准与快速获取[11-12].应用层的主要作用是根据电网的实际情况,从指标层中选择合适的指标组成经济损失评估指标集,通过相应的经济评估方法对各指标进行评估,综合利用各项指标的结果对配电网谐波经济损失进行评估.
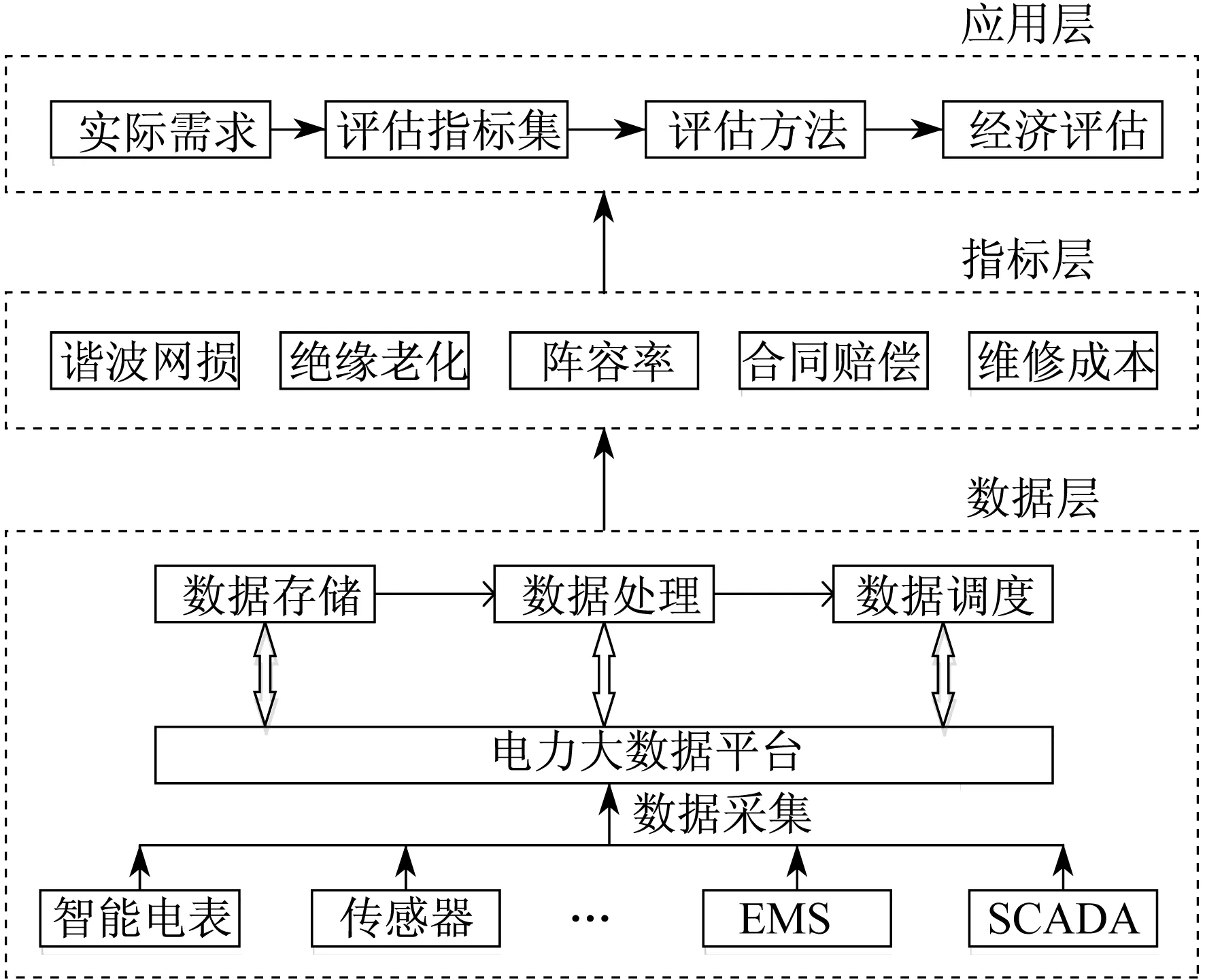
图1 评估体系的总体架构
其中,指标层在整个体系架构中起着承上启下的关键作用,由经济损失评估的主要指标构成,指标的选取不仅决定着谐波经济损失评估的科学性,又是直接展现了大数据在评估过程中的数据价值和发掘程度.为了保证指标能够全面、有效地反映谐波给配电网带来的危害,对评估体系总体架构中指标层的5个一级指标再进行细化,得到二级指标,如表1所示.

表1 评估指标体系
2 基于CAPSO-RBF神经网络谐波网损评估
2.1 混沌自适应粒子群
针对常规粒子群(Particle Swarm Optimization,PSO)算法存在的问题,本文进行以下几点改进,得到混沌自适应粒子群(Chaotic Adaptive Particle Swarm Optimization,CAPSO)算法.
2.1.1 混沌序列初始化
混沌初始化能够提高全局搜索能力和求解效率,目前应用最广泛的混沌映射为Logistic映射.但文献[13]认为,Logistic映射产生的序列不是很均匀,在混沌之后会出现盲点.因此,本文采用立方映射,它比Logistic映射产生的混沌序列更加均匀,遍历性也更强,表达式为:

(1)
对于D维空间的m个粒子,随机产生一个D维向量:Z1=(z11,z12,z13,…,z1D),其中每个分量都在[0,1]之间.根据式(1)产生M个混沌向量,即:Z1,Z2,Z3,…,ZM,将Zk的各分量映入到对应的实际待优化变量的取值范围的映射规则:

(2)
式中:xij——第i个粒子的第j维坐标; xijmax,xijmin——xij的上、下限; zij——第i个混沌向量的第j维坐标.
计算PSO算法适应度函数值,从M个初始群体中挑选出m个性能较优的作为初始解.
2.1.2 自适应惯性权重
惯性权重ω的大小对种群粒子搜索能力的影响很大,本文采用自适应惯性权重,让ω能够跟随种群最优适应度函数值的变化而变化,反映群体进化的实际情况,自适应调节.首先,定义最优适应度函数值变化率.最近3代内,种群最优适应度函数值相对变化率为:
(3)
式中:f(k),f(k-3)——第k代、第k-3代种群最优适应度函数值.
自适应惯性权重ω随ψ的变化而变化:
(4)
式中:ω0——惯性权重初始值; r——[0,1]间的随机数.
由式(4)可以看出,当ψ≥0.05时,表明最近3代的种群最优适应度值还有一定差距,粒子还处于探索阶段,ω应取较大值;当ψ<0.05时,表明最近3代的种群最优适应度值变化较小,粒子已经处于收敛阶段,正在群聚,此时ω应取较小值.
2.1.3 自适应变异
为了描述粒子当前的收敛状态,定义群体适应度方差σ2,计算公式为:
(5)

(6)
式中:fi——第i个粒子的适应度值; favg——群体平均适应度值; f——归一化因子,用来限制σ2大小.
σ2越小,说明粒子越收敛,反之则处于搜索阶段.当σ2很小,且此时的最优解不是理论最优解时,算法可能陷入局部最优解[14].此时,可通过改变当前的全局极值Gbest来改变粒子的搜索方向,使其进入其他区域进行搜索,从而跳出局部最优解,进入新的搜索空间.变异率的计算公式为:
(7)
式中:f(Gbest)——粒子群算法中粒子的适应度函数;
f(s)——粒子群算法中粒子群体的适应度的理论最优值.
考虑 “最小化”情况,自适应变异操作步骤如下:
(1) 根据所有粒子的适应度函数值进行排序,并选取前l个最好的粒子;
(2) 随机产生l个[0,1]之间的随机数μi(i=1,2,3,…,l);
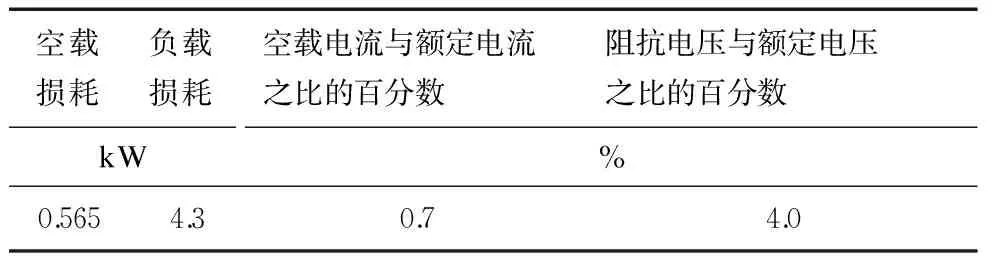
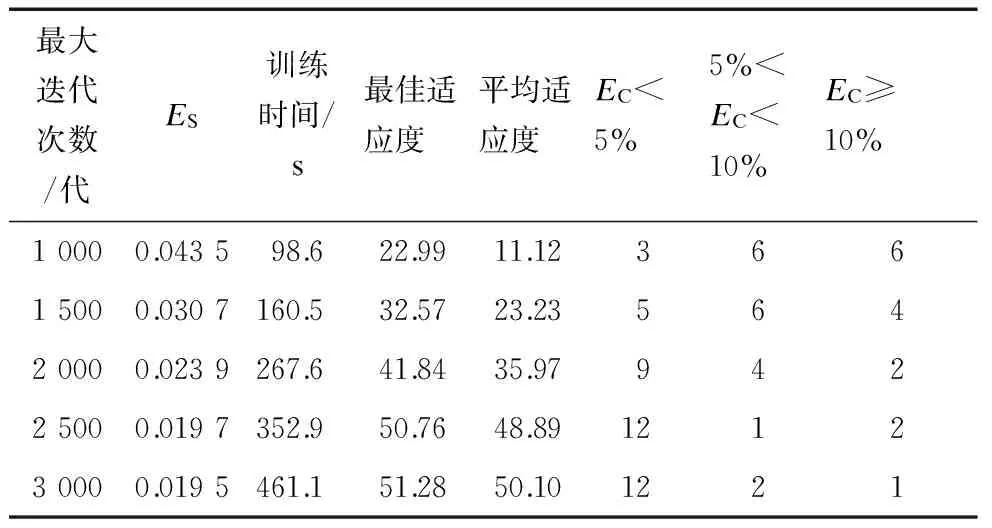
(3) 如果μi (4) 随机产生一个[1,D]间的整数d,xid=xid(1+0.5η),i=1,2,3,…l,其中xid表示第i个粒子的d维坐标,η是服从Gauss(0,1)分布的随机变量. 2.2 CAPSO-RBF神经网络 传统的径向基(Radial Basis Function,RBF)神经网络学习方法大多数都是先通过聚类算法求得径向基函数的中心和宽度,再通过最小二乘等方法求得连接权值.这些方法都是将求解中心、宽度和求解权重分为了两个互相独立的过程,破坏了隐含层、输出层之间的内在联系,失去了RBF神经网络的完整性[15].为了克服以上缺点,本文采用改进后形成的CAPSO算法来对RBF神经网络的结构、参数进行统一优化. CAPSO-RBF神经网络流程图如图2所示. 图2 CAPSO-RBF神经网络整体流程 2.2.1 PSO算法粒子编码 设RBF神经网络的输入层神经元共有n个,隐含层神经元有h个,输出层神经元有m个,粒子位置矢量为Xi,主要由径向基函数的中心C,宽度σ,链接权重ω构成.粒子位置矢量Xi可表示为: 2.2.2 适应度函数构造 对RBF神经网络训练主要是寻找合适的网络参数,从而使网络有较高的预测精度,而这个精度可通过适应度函数来体现.本文的适应度函数为: (8) 式中:Yj(i)——第i个输入样本下的第j个输出节点实际输出值; N——样本个数; m——输出层节点个数. 谐波的存在会加速电力设备的绝缘老化,这种老化是一种长时间的、隐性的影响.由于绝缘老化最直接的后果就是缩短电力设备的使用寿命,带来经济损失.本文主要通过评估电力设备在谐波影响下的寿命损失来量化绝缘老化带来的影响.绝缘老化经济损失M2可表示为: (9) (10) (11) (12) 式中:MT,ML,MC——变压器、电缆线路、电容器老化经济损失; 刑事立法政策是刑事政策在刑法立法上的体现,属于最狭义的刑事政策。然究竟何为刑事政策,目前学界对此的表述可谓林林总总尚无统一的定义,但通说认为刑事政策的概念有广义、狭义和最狭义之分。其中最狭义的刑事政策是指国家或社会公共团体以特别预防为目的,对不同的个别犯罪者或具有犯罪危险者,采取个别的有针对性的抑制活动和强制措施。[1] NT,NL,NC——变压器、电缆线路、电容器数目; LT,LT0,LL,LL0,LC,LC0——谐波影响下的变压器、电缆线路和电容器的实际寿命和设计寿命; PTi,PLi,PCi——第i台(条)变压器、电缆线路、电容器价格; T——评估时间. 谐波影响下的变压器和电容器老化寿命评估模型可分别参考文献[16]和[17],这里不再赘述. 3.1 热-电协同作用下的XLPE电缆老化寿命评估 在实际应用中,电缆绝缘往往会受到如热、电等多种因素的同时作用,需要分析热-电协同作用下的电缆绝缘老化情况,本文通过Simoni模型[18]来对XLPE电缆在热-电协同作用下的老化过程进行描述,剩余寿命为: E≥E0 (13) (14) (15) 式中:L0——电缆在T=T0和E=E0时的寿命,即原设计寿命; B,b,n——试验常数; T0——室温; E0——临界场强. 3.2 谐波影响下的XLPE电缆老化寿命模型 谐波影响下的XLPE电缆线芯温升模型参考文献[19],结合热-电协同作用下的XLPE电缆老化寿命评估研究分析,可以得到谐波影响下的XLPE电缆老化寿命评估模型为: (16) (17) 式中:T*——绝对温度;θ1——谐波作用下电缆线芯温度. 根据式(16)的结果,并结合式(11)就能评估出XLPE电缆绝缘老化寿命经济损失ML. 本文选取某居民小区低压配电网进行谐波经济损失评估.通过查询并筛选出电力大数据平台中该配电网的相关数据,其中变压器型号为s11-400/10,具体变压器参数如表2所示.该变压器0.4 kV侧所用电缆型号为1 kV YJV22电力电缆,相线和中性线导线截面均为120 mm2,相线和中性线长度为0.4 km.变压器的各相谐波含量如表3所示. 表2 变压器参数 表3 各相线和中性线谐波电流数据 A 4.1 基于CAPSO-RBF神经网络的谐波网损评估 对于训练样本,通过在电力大数据平台中进行查询、筛选,一共收集到了17组相关数据.将其中的15组作为学习样本,剩余2组用于测试. 本文选择5个代表性的特性作为RBF神经网络的样本输入,即:变压器基波等效电阻;电缆相线总基波电阻;中性线总基波电阻;三相谐波电流含量均值;中性线谐波电流含量. RBF神经网络输入层节点数为5个,设隐含层节点数目为6个,输出层节点1个,即谐波网损.CAPSO算法中,种群大小为50,迭代次数为3 000,惯性权重ω0为0.5,学习因子c1和c2均为2.0,变异率pm为0.2. 表4中给出了CAPSO算法在不同最大迭代次数下的RBF神经网络训练结果,其中,ES表示样本最佳个体的绝对误差平方和;EC表示为RBF神经网络训练输出结果和实际谐波网损的相对误差百分数,其算式为: 表4 训练结果 由表4可以看出,随着迭代次数的增加,最佳个体的绝对误差平方和在逐渐减小,最佳适应度值和平均适应度值都在逐渐增大.当迭代次数达到了2 500~3 000代时,种群趋于平稳,适应度值变化不大,EC<5%的样本个数也稳定在了12个.这时候最佳适应度值和平均适应度值也比较接近,差距较小,说明此时粒子位置比较集中,可认为CAPSO算法已经收敛,RBF神经网络训练完毕. 图3为最佳个体绝对误差平方和以及种群的平均绝对误差平方和随迭代次数的变化曲线.由图3可以看出,在1 500代之前,种群处于全面探索阶段;1 500~2 500代,两者的曲线变化比较缓慢,种群比较集中,在最优解附近进行局部探索;2 500代后,种群基本稳定,最佳个体和种群的平均绝对误差平方和比较接近,样本训练完成. 图3 误差随迭代次数变化曲线 用训练完毕的RBF神经网络对剩余的两个样本进行精度测试,测试结果如表5所示,其中的实际谐波网损是标准化后的数值. 由表5可以看出,两个测试样本的EC都小于5%,精度较高,说明经过训练后的RBF神经网络可以用来进行谐波网损预测. 表5 样本测试结果 训练后的RBF神经网络对本文案例中的小区低压配电网的预测结果为0.225,将其转换为实际谐波网损值为1 486.98 W,则一年的损失电量为13 025.94 kWh,按照每度电0.52元计算,该配电网一年内由于谐波造成的经济损失达6 773.49元.评估周期为5 a,则经济损失高达33 867.45元. 4.2 电缆线路老化寿命经济损失评估 通过查阅相关资料,获得电缆的结构参数如表6所示. 表6 电缆结构参数 根据文献[20]中的热阻计算方法以及本文中电缆的结构参数,计算得到各层热阻数值如表7所示. 表7 各热阻取值 (K·m2·W-1) 温度计算结果如下:由于谐波(基波除外)引起的线芯相对于环境的温升ΔTh为3.9 ℃,基波引起的线芯相对于环境的温升ΔT1为39.5 ℃,环境温度θe为20 ℃,线芯温度θ1为63.4 ℃. 电缆老化模型参数如下:n=12,b=206 K,B=543 K,L0=30 a,T0=293.15 K. 将上述计算结果及相关参数代入式(16)中,可计算得到电缆剩余寿命L约为24 a.该类型电缆价格为296.15元/m,则一条0.4 km的电缆需要118 460元. 正常情况下,电缆寿命为30 a,年平均折旧费用为3 948.7元;谐波条件下,电缆年平均折旧费用为4 935.8元;则平均每年增加的折旧费用为987.1元,5年共增加折旧费4 935.5元. 4.3 配电网总谐波经济损失评估 根据文献[17]中的变压器绝缘老化寿命评估模型可知,本文变压器剩余寿命为16 a,寿命损失了4 a.该变压器价格按照4万元一台计算,平均每年增加的折旧费用为500元,5年一共增加了2 500元. 对于谐波下的变压器降容率经济损失,本文变压器的降容率计算公式为: (18) (19) (20) 式中:THDI——电流谐波畸变率. 根据表3中数据可计算得到KA为2.015,KB为2.227,KC为2.132,最大为KB,用电流有效值对其进行格式化后得Kh为2.1,D为0.87,即变压器需要降到额定容量的87%运行,才不会导致变压器温度过高或者过载.在谐波的作用下,大约有13%的容量被浪费,即浪费了5 200元. 综上分析,5年内该小区配电网的谐波网损经济损失指标M1为33 867.45元;绝缘老化经济损失指标M2=2 500+4 935.5=7 435.5元;降容率经济损失指标M3为5 200元;由于该小区没有跟供电公司签订电能质量合同,因此M4为零;5年内该小区变压器由于谐波的影响维修过一次,假设维修一次的成本为3 000元,则M5=3 000元.则该配电网5年的谐波经济损失为: 33 867.45+7 435.5+5 200+ 0+3 000=49 502.95元 针对传统谐波网损计算的弊端,本文提出了新的谐波网损评估方法.对常规PSO算法进行改进得到CAPSO算法,并跟RBF神经网络结合,得到了CAPSO-RBF神经网络算法,并应用到谐波网损评估当中.该方法编程较简单,评估结果准确. 另外,本文通过Simoni模型建立了热-电协同作用下的XLPE电缆老化寿命模型,并通过等值热路法建立了谐波影响下的电缆线芯温升模型,将两者结合得到了谐波条件下的XLPE电缆老化寿命模型.算例分析结果表明,谐波含量越高,寿命损失越大,经济损失越严重. [1] 林海雪.连续变化型电能质量的经济评估[J].供用电,2010,27(2):9-12. [2] 林海雪.No.5改善电能质量的经济评估[J].供用电,2016,33(2):34-41. [3] 张占龙,王科,李德文,等.变压器谐波损耗计算及影响因素分析[J].电力系统保护与控制,2011,39(4):68-72. [4] 李琼林,邹磊,刘会金,等.电力变压器谐波损耗仿真计算与实验研究[J].电网技术,2013(12):3 521-3 527. [5] 石碧薇.变压器在谐波条件下的损耗及热问题分析[D].北京:华北电力大学,2014. [6] 江淘莎,李剑,陈伟根,等.油浸式变压器绕组热点温度计算的热路模型[J].高电压技术,2009,35(7):1 635-1 640. [7] 李琼林,李陈莹,庞博,等.谐波对电力电缆损耗的影响分析与计算方法[J].电测与仪表,2015,33(23):34-42. [8] 柳华宁,王建伯,董志敏.谐波对电力电缆线路损耗的影响[J].河北电力技术,2009,28(3):25-28. [9] 陈海涵,程启诚.等值电阻法计算配电网损耗的理论和实践[J].广东电力,2004,17(3):5-8. [10] 李文才,李燕,王希平,等.低压配电网的谐波损耗与综合治理[J].电气应用,2009,28(3):48-50. [11] 彭小圣,邓迪元,程时杰,等.面向智能电网应用的电力大数据关键技术[J].中国电机工程学报,2015,35(3):503-511. [12] 张东霞,苗新,刘丽平,等.智能电网大数据技术发展研究[J].中国电机工程学报,2015,35(1):2-12. [13] 王涛.基于捕食搜索策略的自适应混沌粒子群算法的研究及应用[D].广州:暨南大学,2013. [14] 吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报,2004,32(3):416-420. [15] 赵建玉,贾磊,杨立才,等.基于粒子群优化的RBF神经网络交通流预测[J].公路交通科技,2006,23(7):116-119. [16] 温惠,王同勋,毛涛,等.基于谐波畸变率和负载率的变压器损耗及寿命损失分析[J].电测与仪表,2015,52(22):42-48. [17] 宁凤辉,段乃欣,邱毓昌.金属化膜电容器受谐波影响的寿命模型[J].绝缘材料,2002,35(5):21-23. [18] MONTANARI G C,MAZZANTI G,SIMONI L.Progress in electrothermal life modeling of electrical insulation during the last decades[J].IEEE Transactions on Dielectrics and Electrical Insulation,2002,9 (5):730-755. [19] 李海英,刘毅超,宋建成.谐波对矿用XLPE电缆容量和稳态温度的影响[J].高压电器,2014(9):82-88. [20] 马国栋.电线电缆载流量[M].北京:中国电力出版社,2003:45-60. (编辑 桂金星) Study on Economic Loss Evaluation Method of Harmonic Wave in Distribution Network Based on Large Data DAI Chaofan1, DENG Xiaoxiang1, JIANG Yu2, DING Xiaoqun2, DENG Jixiang3 (1.HeilongjiangInstituteofScienceandTechnology,Harbin150022,China;2.CollegeofEnergyandElectricalEngineering,HehaiUniversity,Nanjing211100,China;3.TaizhouPowerSupplyCompany,Taizhou225300,China) At present,a unified scientific evaluation system is absent.In view of this problem,based on the power large data technology,the overall framework of harmonic economy loss evaluation system of distribution network which contaions data layer,index layer and application layer is constructed and the harmonic economy loss evaluation index system is established.The conventional particle swarm optimization algorithm is improved,in combination with the RBF neural network,using the CAPSO-RBF neural network to assess the harmonic loss.The Simoni model and the XLPE cable harmonic line core temperature rise model are combined,obtaining the evaluation model of insulation aging life of XLPE cable.Finally,the feasibility of this method is proved by the case analysis,and the rationality of the evaluation system and the advantages of large power data is also verified. large data; distribution network; harmonic economy loss 10.3969/j.issn.1006-4729.2017.02.008 2017-01-09 戴超凡(1991-),男,在读硕士,江苏宿迁人.主要研究方向为无功补偿与谐波抑制.E-mail:200878904@qq.com. TM727;TM711 A 1006-4729(2017)02-0145-07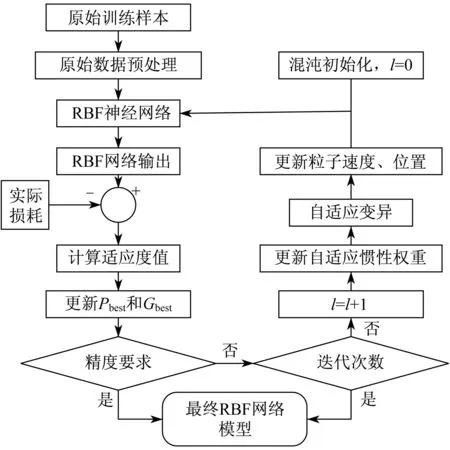
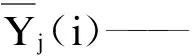
3 配电网电力设备绝缘老化寿命经济损失
4 算例分析





5 结 语

