单抽汽轮机热电耦合的模糊解耦控制

李 艳， 拓福婷， 刘丽芳

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西农产品加工技术研究院， 陕西 西安 710021； 3.陕西科技大学 职业教育师范学院， 陕西 西安 710021)



单抽汽轮机热电耦合的模糊解耦控制

李 艳1,2， 拓福婷1， 刘丽芳3

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西农产品加工技术研究院， 陕西 西安 710021； 3.陕西科技大学 职业教育师范学院， 陕西 西安 710021)

抽汽式汽轮机存在着热负荷、电负荷之间的强耦合以及参数的不确定性问题，其中任一负荷的变化都会引起另一个的波动，进而影响整个汽轮机控制系统的性能.针对上述问题，以某造纸厂热电厂6 MW单抽汽轮机为例，在分析其工作原理的基础上应用机理法建立了系统数学模型.其次，分析了其强耦合特性，根据实际需要设计了模糊解耦控制方法以实现热电解耦及提高系统适应性.最后，进行了Matlab/Simulink仿真实验，结果表明，与常规对角解耦相比，该方法在强耦合及模型参数存在一定波动时，仍能保证较好的稳定性及鲁棒性.

汽轮机; 热电负荷耦合; 数学模型; 模糊解耦控制

0 引言

抽汽式汽轮机是一类既能供热又能供电的原动机械，是目前实现热电联产的主要形式之一，具有能源利用合理，循环热效率高、运行方式灵活、适用范围广的特点，因此受到广泛的重视和应用，主要包括化工、造纸、发电等行业[1,2].但抽汽式汽轮机结构复杂，存在强热电耦合特性，为保证供热和供电品质，就要选择合适的控制方案及控制器参数.因此，实现汽轮机热电解耦控制具有十分重要的意义，也是目前研究的重点问题之一[3].

针对抽汽式汽轮机热电强耦合特性引起的系统输出频繁波动的问题，国内外许多科研机构和高校进行了大量的理论分析和实验研究[2-6].文献[2]将功率变化对热负荷的影响通过加权系数叠加在控制热负荷变化的阀门上，来消除热电耦合，其本质是对角解耦.虽然实现了系统静态解耦，但严重依赖于解耦系数的准确性.文献[3]提出了分块线性化的热-电负荷比例解耦控制算法，并给出了基于非线性工况图的比例系数计算方法.该方法能够实现系统静态解耦及准动态解耦，但存在对系统非线性工况图准确性要求较高的问题.文献[4]提出利用电液控制电信号处理方便的优点实现系统电负荷与热负荷的解耦，但也要求精确的数学模型，不适用于含有不确定性参数的系统.文献[5,6]以某小型双抽汽轮机为被控对象，建立了其动态数学模型，用BP神经网络实现其解耦控制并提出了基于模糊神经网络的双抽汽轮机解耦控制的方法，该方法能够有效实现热电解耦控制，但其算法复杂，不易实现.文献[7,8]应用神经网络解耦也有相同的问题.

上述方法为汽轮机的解耦控制技术的发展做出了贡献,但仍然存在一些不足.首先，传统的对角解耦方法中的解耦系数都是在系统参数确定的情况下，根据多变量解耦理论通过精确计算得到的，对系统精确模型依赖性过高.其次，神经网络存在需要数据量巨大，训练时间长等缺点.文献[9-14]分别将模糊控制理论应用于有各类强耦合系统的解耦控制，虽然方法有所不同但都取得了良好的控制效果，证明模糊控制在解耦控制领域具有一定的优势.

根据上述分析，本文在完成抽汽式汽轮机机理建模的基础上，提出了一种PI控制与模糊解耦相结合的控制方法.PI控制具有良好的稳态性能及快速跟踪性，是一种应用广泛的控制器.模糊逻辑控制具有不依赖对象精确数学模型、对模型参数变化不敏感以及算法简单等优点，是处理参数不确定、非线性、多变量强耦合系统的一种有效的方法[14].因此将二者结合，可以在实现系统解耦的基础上提高系统的适应性、鲁棒性.本文以某造纸厂热电厂6MW汽轮机组为例进行研究，汽轮机是由青岛捷能汽轮机集团股份有限公司生产的C6-4.90/0.686单抽汽式汽轮机.

1 系统描述及数学模型的建立

1.1 系统描述

抽汽式汽轮机的详细模型较复杂，通常在仿真实验研究中采用较为简化的结构，典型的单抽汽轮机的结构如图 1 所示[1].

图1 单抽汽轮机结构

图1中：1-高压缸， 2-低压缸 ，3-凝汽器，4-热用户， 5-高压调节阀 ，6-低压调节阀 ，7-发电机.这7部分是典型的单抽汽轮机的主要组成环节.其工作原理为：主蒸汽经过高压调节阀，进入高压缸，膨胀做功后一部分经低压调节阀进入低压缸继续做功直至凝汽器，另一部分由抽汽口引出到蒸汽容积用于为热用户供热.

当热负荷增加时，为保证总功率电负荷不发生变化，相应地就要增大高压调节阀的开度，减小低压调节阀的开度.同理，当所需的电负荷发生变化时，同时增大高、低压调节阀的开度，以保证电负荷保持不变.因此通过高、低压调节阀开度的协调调节就可以同时控制汽轮机总功率及供热压力的稳定.

1.2 系统数学模型的建立

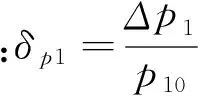
1.2.1 液压放大元件及执行元件

滑阀油动机是目前广泛应用的一类液压放大元件及执行元件，主要包括错油门、油动机、反馈机构三部分.其输入量为控制滑阀位移ΔSx，输出量为油动机活塞位移ΔSz.在不考虑惯性力及初始状态为平衡状态的条件下，滑阀油动机模型如图2所示[1].

图2 滑阀油动机的传递函数框图

其中，Ks为油动机机构的静态放大倍数；Th为油动机滑阀时间常数；Ts为油动机时间常数.由于Th≪Ts，则滑阀油动机机构的传递函数为：

(1)

1.2.2 高、低压容积方程

单抽汽轮机蒸汽容积分为高压蒸汽容积和低压蒸汽容积，高压蒸汽容积的物理模型如图3所示.

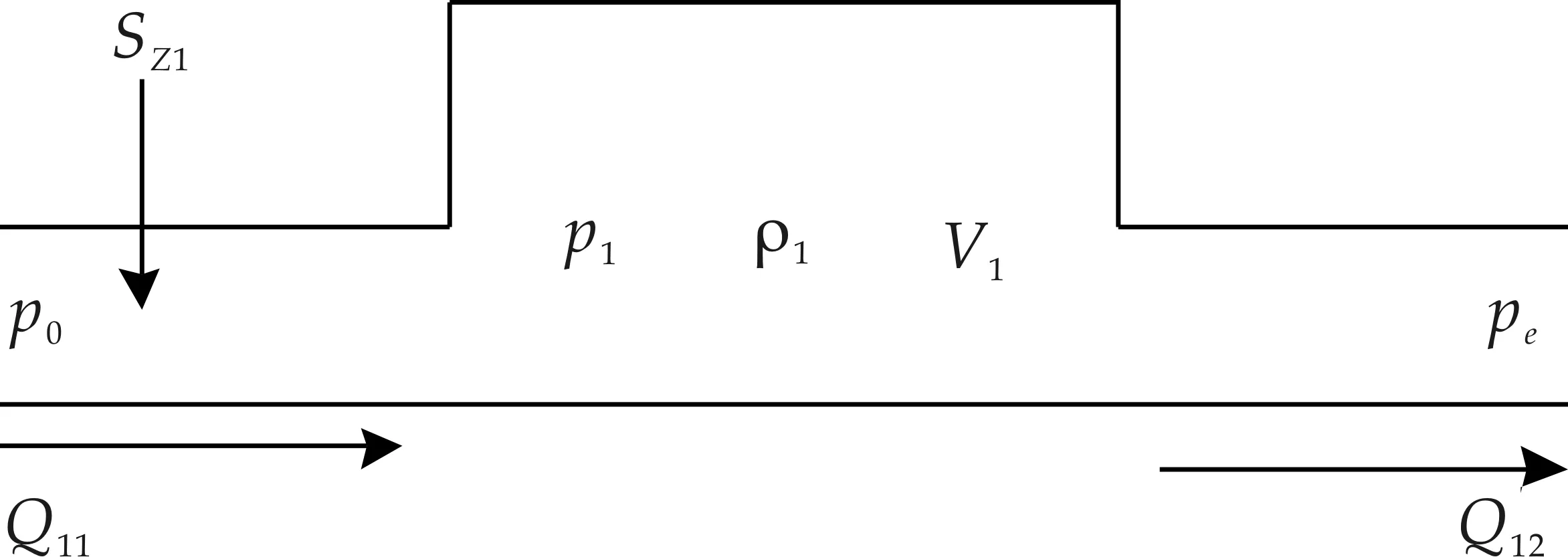
图3 高压蒸汽容积物理模型

对于图3所示的高压蒸汽容积，在不考虑pe对排汽量Q12影响及p1对进汽量Q11的影响的前提下，Q11主要受p0、Sz1的影响，Q12主要由p1决定.则根据质量守恒定律可得：

(2)

式(2)中：p1、ρ1、V1分别为高压容积的压力、密度、体积；Q11、Q12分别为其进汽量、排汽量；p0、pe分别为主蒸汽压力和抽汽供热压力，Sz1为高压调节阀开度.

设高压容积的过程为指数为n的多变过程[9]，由气体多变过程状态方程可得：

(3)

在工作点(p00、p10、ρ10、Sz10)附近取变化量(Δp0、Δp1、Δρ1、ΔSz1)，考虑额定工况下Q11=Q12，同时有Δp0≪p00，Δp1≪p10，Δρ1≪ρ10,对式(3)进行小偏差线性化处理并将方程中各变量用其相应额定值的百分比表示：

(4)

在假定系统投入运行后主蒸汽压力不发生较明显变化的前提下，方程两边同时除以Q110对式(4)进行标幺化，则式(4)可简化为：

(5)

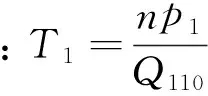
同理，可得低压蒸汽容积方程为：

(6)

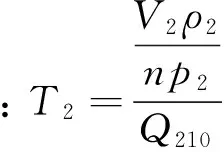
1.2.3 抽汽容积

抽汽容积的物理模型如图4所示.图(4)中的低压容积进汽流量为Q21(不考虑p2对其影响)，主要由受pe和Sz2的影响.Qe由pe和抽汽时间t决定.根据质量守恒定律得：

(7)

式(7)中：pe、ρe、Ve分别为抽汽容积压力、密度、体积；Q21为低压容积进汽流量；Qe为供热蒸汽流量，t为抽汽时间.

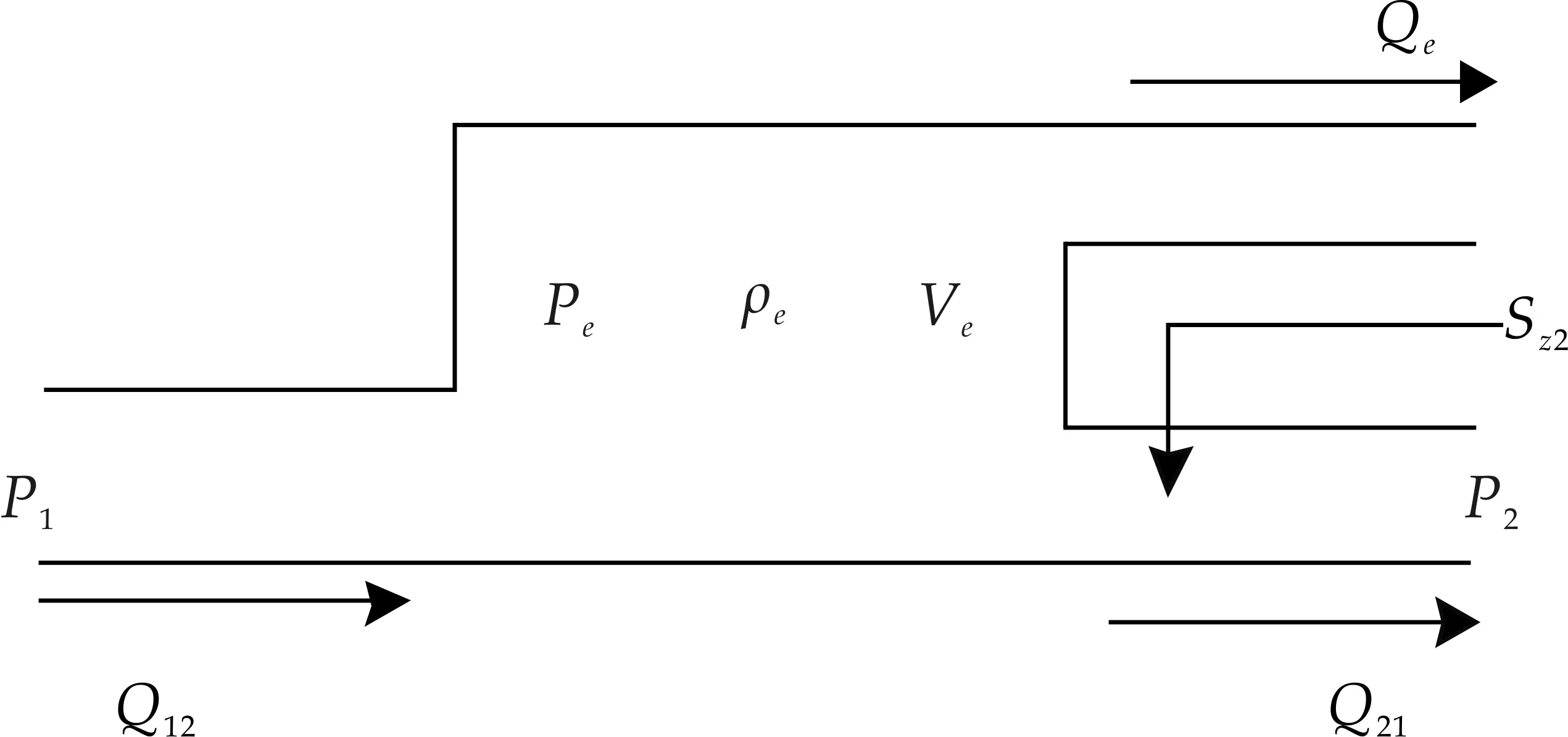
图4 抽汽容积物理模型

在工作点附近做小偏差线性化(各变量用百分比表示)，取线性部分：

(8)

对式(8)进行标幺化，两边同时除以高压容积排汽量额定值Q120得(此处不考虑热负荷扰动)：

(9)

1.2.4 转子方程

汽轮机转子功率的决定性因素有三个：蒸汽功率NT、负荷消耗功率NL、摩擦功率Nf.则由功率平衡原理可得:

(10)

式 (10)中：J为转子的转动惯量，ω为转子的角速度.Nf为ω的非线性函数，可表示为Nf(ω).NL为电负荷扰动，在进行模型建立时不考虑该扰动. 蒸汽功率：

NT=N1+N2

N1=ΔH1Q12(p1)η1

N2=ΔH2Q22(p2)η2

(11)

式(11)中：N1，N2分别为高压容积、低压容积的蒸汽功率；ΔH1、ΔH2和η1、η2分别为高压缸和低压缸的焓降和功率因子，建模时，假定其不变.

将式(11)代入式(10)，并对其进行小偏差线性化得：

(12)

对式(12)进行标幺化(不考虑电负荷扰动NL)得转子方程为：

(13)

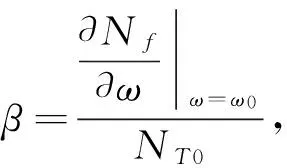
综上，根据式(1)、(5)、(6)、(9)、(13)，可得单抽汽轮机耦合系统结构图，如图5所示(通常假定进汽量与调节阀开度成正比同时进汽量与容积压力成正比，则k11，k12，k21,k22,ke2,ke3通常均取1).

图5 单抽汽轮机数学模型

其中,Ts1，Ts2分别为两个控制回路的滑阀油动机时间常数,Ks1、Ks2分别为两个油动机机构的静态放大倍数.

2 系统耦合特性分析及解耦控制器设计

2.1 耦合特性分析

多变量系统各回路之间存在耦合，是指系统的某个输入与系统的所有输出之间相互影响或系统的某一输出受所有输入的影响[15].由上述分析可知汽轮机系统是一个两入两出的多变量系统.输入为高、低压调节阀的开度，输出为转速和抽汽压力，且高压、低压任一调节阀的开度发生变化都会引起两个输出量的变化.例如，高压调节阀开度增大，则汽轮机总功率和抽汽压力都会增大.因此，汽轮机系统是一个典型的多变量、强耦合系统.

2.2 解耦控制方案结构设计

汽轮机系统解耦控制的目标是实现高、低压调节阀对汽轮机总功率和抽汽压力的独立控制，互不影响.本文提出的模糊解耦控制方案结构框图如图6所示.

图6 模糊解耦控制方案结构

解耦方案中，分别用转速和抽汽压力表示汽轮机电负荷和热负荷.其控制原理是：将两入两出的多变量耦合系统通过两个PI控制器和两个模糊解耦器转化为两个两入单出的控制系统.首先通过模糊解耦器实现系统解耦，然后通过两个PI控制器依次实现单个回路的控制.

3 模糊解耦器及PI控制器的设计

3.1 模糊解耦器设计

本文采用二维输入，9*7模糊规则的模糊控制器，由模糊化、模糊推理、解模糊三部分组成.下面以解耦控制器FC1为例进行说明.输入信号分别为转速PI控制器输出信号和压力PI控制器输出信号.

(1)模糊变量设计及隶属度函数选择

假定模糊控制器的输入变量分别为C11、C12，论域为[-6,6].输出变量为U1，其模糊论域为[-10,10].将模糊变量C11、输出变量U1的论域划分为9个模糊子集，{NB，NM，NS，NW，Z，PW，PS，PM，PB}，模糊变量C12划分为7个模糊子集，{NB，NM，NS，Z，PS，PM，PB}.

根据三角形隶属度函数控制灵敏度高，分辨率高的特点，在PI控制器输出相对小的时候选用三角形隶属度函数.同时为了保证系统的稳态性能，在PI控制器输出值较大时选用S和Z型隶属度函数，当其输出值适中时，选用梯形隶属度函数，即可得模糊解耦器1输入变量C11的隶属度函数.依据相似的设计原理，其余各变量的隶属度函数如图7所示.

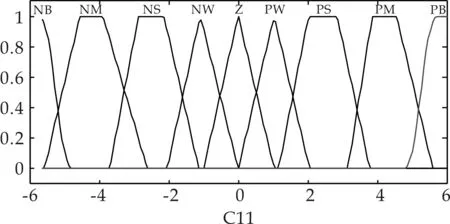
(a)C11的隶属度函数

(b)C12的隶属度函数

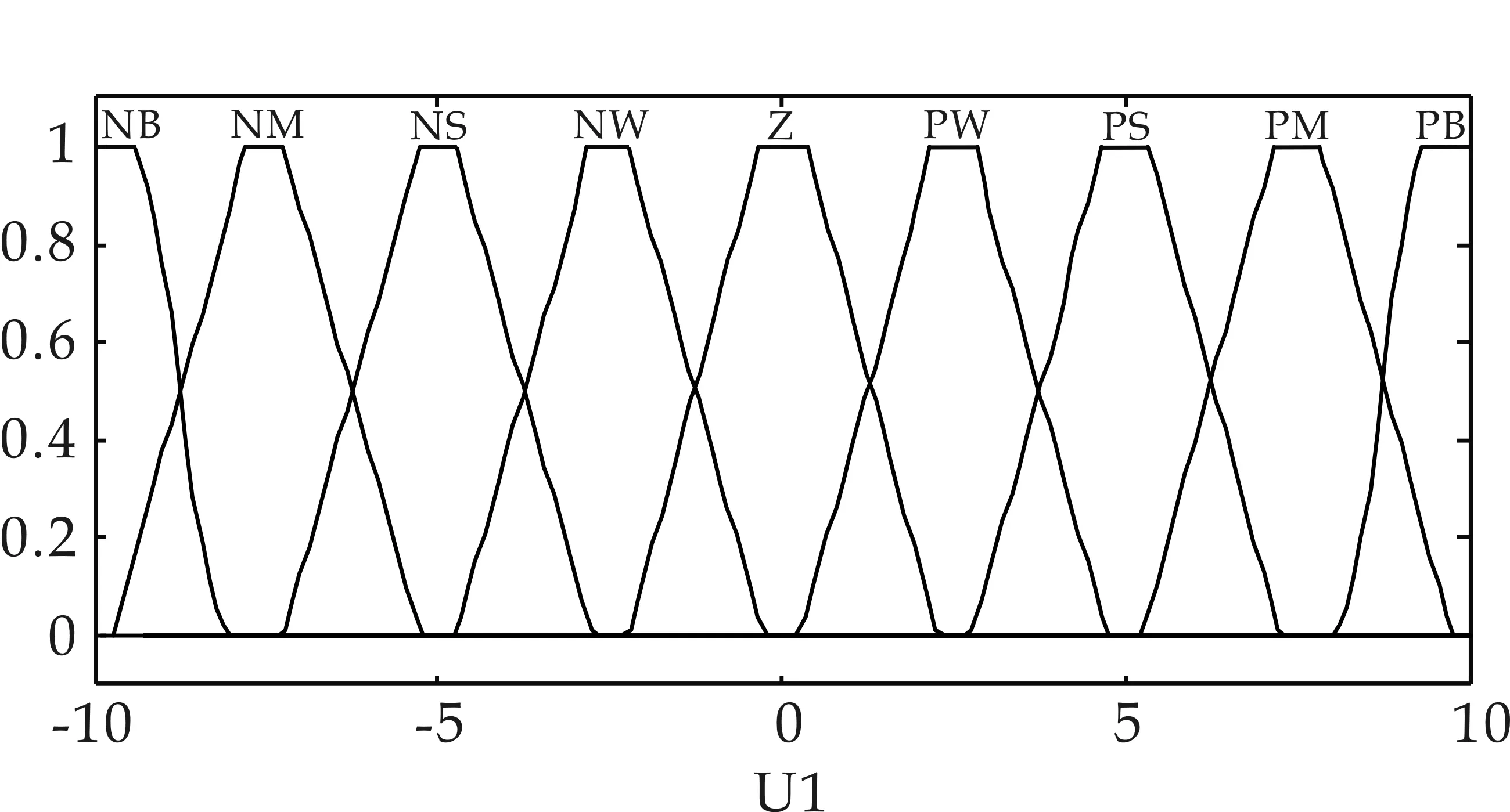
(c)U1的隶属度函数图7 模糊解耦控制器1的隶属度函数

(2)模糊规则设计及解模糊

在本文所设计的模糊解耦控制系统中，模糊控制器的主要作用是解耦，模糊规则根据以下思路建立：当系统电负荷增加时，则系统实际转速低于设定转速，如果仅通过增大高压调节阀的开度来调节，则C11增大，U1增大，调节阀开度增大.但由于耦合关系的存在，此时若C12也增大，则抽汽压力也低于设定值，根据单抽汽轮机调节原理，则模糊控制器U1应进一步增大.

根据上述思路及实际控制需求，可建立如表1所示的FC1的全部模糊控制规则.

表1 模糊解耦器1的模糊规则表

为获取准确的控制量，本文选取重心法解模糊方法，其表达式为：

(14)

用类似的方法可完成模糊解耦控制器2的设计.

3.2 转速及压力控制器设计

基于PI控制器快速跟踪输入，消除静态误差的特点，本文选用PI控制器作为转速和压力控制器.PI控制器包含比例，积分两部分，其控制算法如下：

(15)

对于转速控制回路，系统输出的转速经过调速器中的转速测量元件测量后反馈至系统输入端，与给定的转速比较，从而得到转速PI控制器的输入信号.压力PI控制器设计思路同转速PI控制器.

4 系统仿真实验

为验证所设计控制方案的有效性，笔者采用上述6 MW汽轮机组数据进行数字仿真研究，图5中数学模型的各参数如下：油动机时间常数Ts1=Ts2=0.2，各蒸汽容积时间常数介于0.1～0.3，高压缸功率系数Kn1=0.6，低压缸功率系数Kn2=0.4，抽汽流量比Ke=0.4，转自时间常数Ta=11.8，自平衡系数β=1.

在Matlab/Simulink图形化建模环境下，根据上述理论分析及实际数据建立如图8所示的仿真模型.

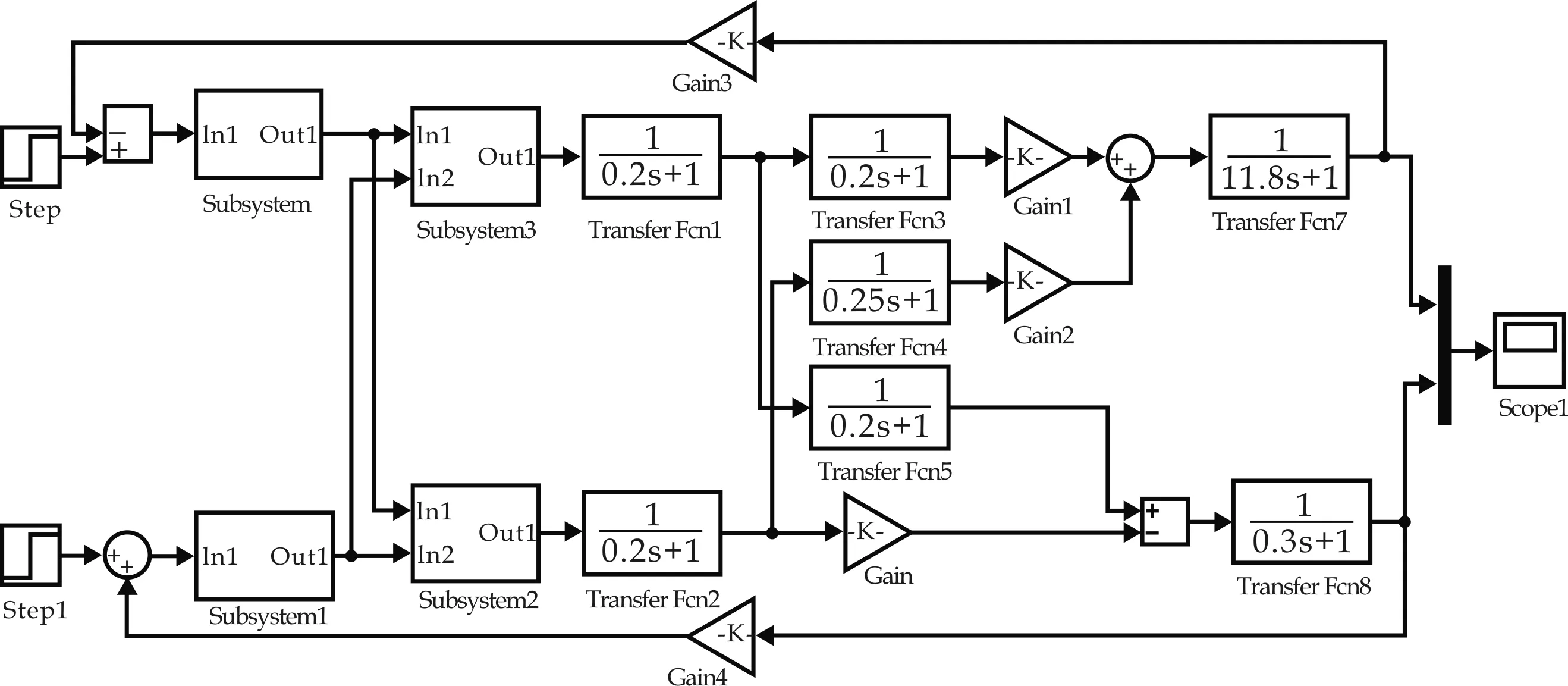
图8 模糊解耦控制Simulink仿真模型

图8中各输入量的量化因子由模糊子集论域的最大绝对值与其基本论域的最大绝对值作商求得，而输出变量的比例因子由其基本论域的最大绝对值与相应的模糊子集论域的最大绝对值作商得到.根据上述理论计算可得k11=1.5,k12=3,ku1=0.5.具体仿真实验过程中，通过Matlab/Simulink仿真平台中Signal Constraints进行调整，得：k11=2,k12=4,ku1=0.65.控制系统中的PI控制器参数可通过试误法获得，其中kp1=4.2,ki1=2,Ti1=0.2;kp2=5,ki2=1.2,Ti2=1.1.

仿真实验中，分别当0 s和20 s时在电负荷控制回路和热负荷控制回路中加入终值为1的阶跃信号，仿真时间为60 s.解耦效果仿真结果如图9、10所示.其中,图9为未解耦时的响应曲线，图10中(a)、(b)分别为模糊解耦控制和对角解耦控制的仿真结果.

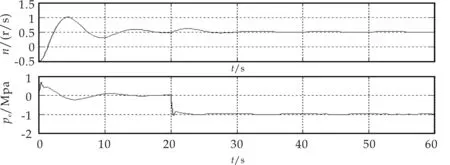
图9 系统耦合响应曲线

通过对上述仿真结果的分析可知：对于给定的单位阶跃输入信号，采用对角解耦时虽然能够实现有效解耦但电负荷控制回路输出的转速达到了300%的超调，压力控制回路中，抽气压达到了100%的超调.而采用模糊解耦控制时单抽汽轮机系统运行平稳，在电负荷和热负荷突变时系统输出波动在3%以内，有效地抑制了汽轮机转速和抽汽压力的波动，最终实现了单抽汽轮机系统的高效，快速的解耦控制.

为验证系统的适应性、鲁棒性及抗干扰能力，笔者还根据实际生产情况，就油动机时间常数发生变化及系统加入电负荷扰动的情况作了仿真对比.仿真结果如图11(a)、(b)、(c)、(d)所示.

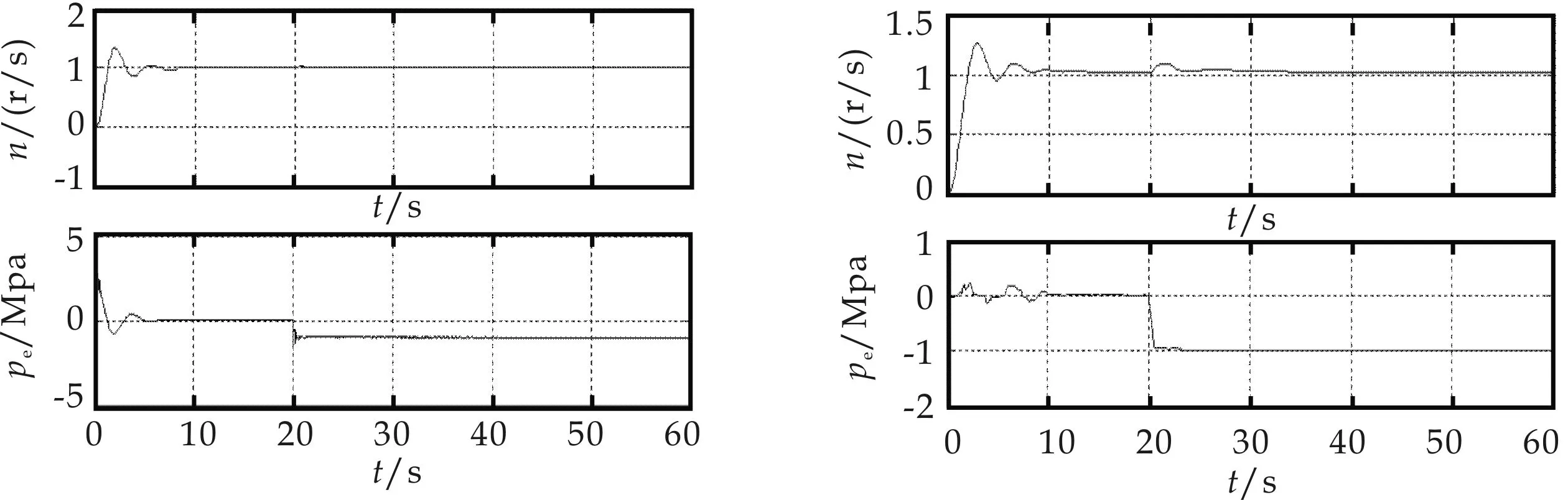
(a)油动机1时间常数变 (b)油动机1时间常数变

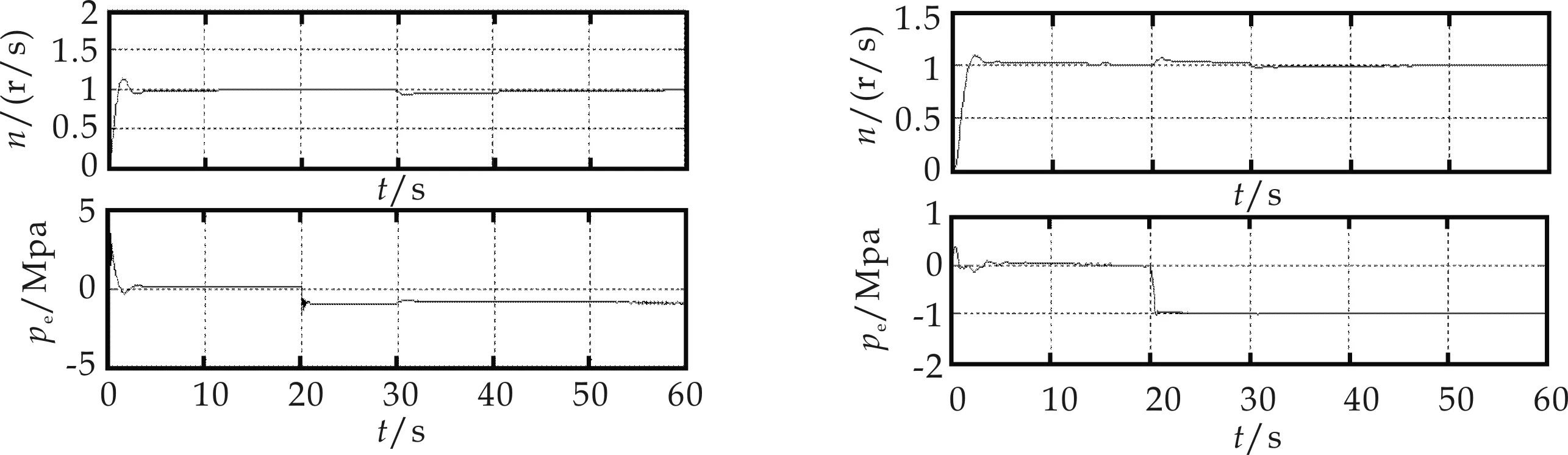
(c)加入电负荷扰 (d)加入电负荷扰图11 解耦控制系统性能测试响应曲线

图11中(a)、(b)分别为单抽汽轮机耦合系统中油动机1时间常数发生25%的变化时的对角解耦和模糊解耦控制仿真结果.由仿真结果可知：当油动机时间常数发生变化时，对角解耦控制系统对于电负荷的突变，其转速响应曲线超调大，调节时间长，同时抽汽压力回路的输出有明显的波动和超调.而采用模糊解耦控制时，系统响应速度加快，超调减小，仍然具有良好的鲁棒性、跟踪性，并能有效的实现系统解耦.

图(11)(c)、(d)分别为在第30 s时加入100%的电负荷扰动后的对角解耦控制和模糊解耦控制响应曲线图.从图中可以看出第30 s时，对角解耦控制中抽汽压力的响应曲线发生明显的波动且过渡时间长.而采用模糊解耦时抽汽压力响应曲线几乎不受影响，系统具有更好的解耦效果及抗干扰能力.

5 结论

本文针对汽轮机系统存在强耦合及时变的特点，以解除热电耦合以及提高控制系统对参数波动的适应性为目的，采用模糊控制器作为解耦器，设计了一种基于模糊解耦控制的单抽汽轮机控制系统.仿真结果表明本系统不仅具有较强的抗干扰能力、鲁棒性，而且能有效地实现单抽汽轮机的热电解耦控制，同时该控制系统对参数变化具有较好的适应性.

[1] 郭钰峰,徐志强,于达仁.汽轮机调节原理[M].2版.北京:机械工业出版社,2010.

[2] 唐 丽.抽汽式汽轮机热电牵连解耦控制的研究与应用[J].电站系统工程,2009,25(1):61-63.

[3] 史毅越.抽汽式汽轮机的模型辨识及热电解耦[D].南京:东南大学,2014.

[4] 纪云锋.抽汽汽轮机组DEH系统的解耦控制[J].液压与气动,2007(5):49-50.

[5] 裘浔隽,杨瑜文,林中达.用多变量模糊神经网络实现双抽汽轮机热电负荷的解耦控制[J].汽轮机技术,2003,45(2):76-79.

[6] 吴优福,裘浔隽.用神经网络实现双抽汽轮机的负荷解耦控制及仿真[J].能源研究与利用,2003(1):29-32，40.

[7] 陈 蓓,田 娜,姚 培.基于单神经元自适应PID的水分定量内模解耦控制[J].陕西科技大学学报(自然科学版),2008,26(3):91-95.

[8] 高希明,孟彦京.一种基于神经元的解耦控制算法研究[J].陕西科技大学学报(自然科学版),2009,27(1):110-113.

[9] 胡 灿,田小梅.基于耦合度分析的家禽孵化过程模糊解耦控制系统[J].衡阳师范学院学报,2016,37(3):26-29.

[10] 麦雪凤,宁甲宇.焦炉集气管压力模糊解耦及吸力协调控制与应用[J].冶金自动化,2015,39(1):72-76.

[11] 王 茹,陶泽炎.基于模糊前馈解耦的变风量空调控制方法研究[J].计算机测量与控制,2015,23(2):450-453，456.

[12] 王昕煜,赵静一,徐丽杰.桥梁同步顶升模糊解耦控制策略研究[J].中国工程机械学报,2015,13(4):347-352，371.

[13] 王江鹏.基于模糊解耦的精馏塔温度控制的仿真研究[D].昆明：昆明理工大学,2015.

[14] 张 玲,张文苑,郑恩让.一种模糊解耦控制系统的设计与仿真研究[J].计算机仿真,2010,27(8):118-121.

[15] 柴天佑.多变量自适应解耦控制及应用[M].北京：科学出版社，2001.

【责任编辑：陈 佳】

Fuzzy decoupling control of thermo-electric coupling single extraction turbine

LI Yan1,2， TUO Fu-ting1， LIU Li-fang3

(1.College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.Shaanxi Research Institute of Agricultural Products Processing Technology, Xi′an 710021, China; 3.College of Vocational Normal Education, Shaanxi University of Science & Technology, Xi′an 710021， China)

Parameter uncertainty and serious coupling relationship exists between heat load and electric load are two major problem in extraction steam turbine,a small change in either load of the two will cause further fluctuations,thereby affecting the performance of the turbine control system.To solve these problems,taking a 6 MW single extraction steam turbine from power plant of a paper mill as a case.Based on the analysis of its working principle we establish a mathematical model.Then,we analysis its strong coupling characteristics,and design a fuzzy decoupling control method to achieve decoupling and improve the thermoelectric system adaptability,according to the actual need .Finally,the Matlab / Simulink simulation results show that,compared to conventional diagonal decoupling,the method in strong coupling model parameters and there are some fluctuations,it can still ensure better stability and robustness.

turbine； thermoelectric load coupling； mathematical model； fuzzy decoupling control

2016-11-27

陕西省科技厅科学技术研究发展计划项目(2013K07-28)； 陕西省教育厅专项科研计划项目(14JK1094)

李 艳(1972-)，女，四川仁寿人，副教授，硕士，研究方向：工业自动化、智能检测与智能控制

2096-398X(2017)03-0159-07

TK261

A