致密油藏细分注水的模糊数学判别法

徐 杨， 张 涛， 梁 聪， 程时清*， 王 斌

(1.中法渤海地质服务有限公司 湛江分公司， 广东 湛江 524057; 2.中国石油大学(北京) 石油工程教育部重点实验室， 北京 昌平 102249； 3.中国石油长庆油田分公司 勘探开发研究院， 陕西 西安 710021 )



致密油藏细分注水的模糊数学判别法

徐 杨1， 张 涛1， 梁 聪2， 程时清2*， 王 斌3

(1.中法渤海地质服务有限公司 湛江分公司， 广东 湛江 524057; 2.中国石油大学(北京) 石油工程教育部重点实验室， 北京 昌平 102249； 3.中国石油长庆油田分公司 勘探开发研究院， 陕西 西安 710021 )

针对致密油藏，提出用连通井数与连通井距来描述开发因素对注水井纵向吸水能力的影响.结合静态地质因素，如渗透率级差和有效厚度，采用模糊判别法来选择分注井.通过计算渗透率级差、有效厚度、连通井数变异系数以及连通井距变异系数的隶属函数来确定单因素决策因子，利用求和法与方根法计算权重系数，建立一套有效的致密油藏分注井判别法.并应用L1油藏实际分注资料进行验证，证明该方法的适用性和可靠性.

致密储层； 细分注水； 吸水能力； 模糊数学法； 权重系数

0 引言

细分注水就是根据储层纵向非均质性，把性质相近的小层组合一个层段进行注水，而把物性差异大的小层分开注水，减轻层间干扰，达到提高小层动用程度的目的[1]，细分注水是控制无效注水、提高储层动用程度的一项有效措施[2].注水井细分注水的关键在于其技术界限的制定.一般根据吸水剖面等开发动态资料及数值模拟方法划定技术界限[3-5]，这些方法主要针对常规中高渗油藏，只考虑了单因素或静态地质因素对分层注水的影响[6-9]，没有将实际开发的多种因素综合加以考虑.同时，在选择分注井时，多采用定性分析法，没有对各指标进行量化，分析不同因素在分注井选择时的权重.

致密油藏作为重要的非常规油气藏，已经成为国内外研究的重点，目前国内致密油藏开发方式仍然以注水为主，但笼统注水很难达到致密油藏配注要求，导致地层能量保持水平低，油层动用程度低，开发效果差.将常规油藏细分注水方式应用到致密油藏，技术上还不成熟，成功的案例还不多.本文针对致密油藏特征，提出用连通井数和连通井距来刻画开发因素对纵向吸水能力的影响，同时还考虑了渗透率级差、油层有效厚度等地质因素，应用模糊数学[6-8]方法确定分注井.

1 注水井纵向吸水能力的影响因素

1.1 渗透率级差

渗透率级差对于注入水在储层纵向上的分布有着重要的影响.一般高渗层渗流阻力小，吸水能力较强，小层见水较快，从而造成油井含水率上升快的现象，而低渗层由于受到高渗层的影响，吸水量受到抑制，这就导致油藏纵向上吸水不均匀，部分层段不吸水，加剧了层间矛盾.因此渗透率级差越大，注水井越应该进行分注.L1油藏是陕甘宁盆地的一个致密油藏，2007年全面投入开发，截止到2013年9月共有开井的油井1116口，注水井395口，其中分注水井78口.按照排列位置、渗透率以及产液量等因素划分为五个区块.该区块砂层组为C81和C82，根据次一级沉积旋回，又将油层划分成C811、C812、C821和C822共4个小层，按短期沉积旋回，又进一步将其划分为C811-1、C811-2、C812-1、C812-2、C821-1、C821-2、C822-1和C822-2共8个单砂层.C81亚油组的有利储层主要分布在C811-1和C811-2，C82亚油组的有利储层主要分布在C822-1和C822-2.C811层为该区主力小层，该层分布较为连续，砂体展布广泛；C812层则多分布于1、2、3、4区，且不太连续，C821层砂体较为分散，可作为稳定的隔层存在，而C822层则仅存在于5区，且分布稳定，故分注井组在平面上多存在于2区及5区，纵向上则为C811与C812之间或C821与C822之间；总体上看，L1油藏非均质性强，从吸水剖面测试资料看出，注入水沿高渗层指进.吸水剖面表现为尖峰状或指状，对应油井含水上升快，见效期短，增油效果差.

1.2 有效厚度

在注水开采过程中，油层的有效厚度也是影响油藏开采效果的重要因素，如果层段过厚，则不宜采用一套层系笼统注水，应进行分层注水，主要是因为厚度大，在纵向上难以形成均匀驱替，注入水在高渗层其内容易形成优势通道，导致部分厚度难以被水驱到，从而降低纵向动用程度.因此有效厚度越大，注水井越应该进行分注.

针对L1油藏的特点，进行了数值模拟计算，对比研究了有效厚度分别为4 m、8 m、12 m、16 m、20 m的含水率与采出程度关系曲线，发现当厚度大于12 m时，注水井的波及面积以及油层的动用程度明显降低，且部分油井出现未被波及到的现象.对比分析了分注井和笼统注水井的油层有效厚度，也说明了12 m以上分注比不分注效果好.

1.3 连通井数

以上两个因素均为静态地质因素，在实际注水过程中，还须考虑开发因素的影响.首先是连通井数，它与油藏的开采方式，布井方式均有关系，即人为因素影响很大.和常规中高渗油藏不同，一般来说致密油藏的储层非均质性更为严重.如若采用笼统注水方式，易在高渗层段注入水波及较快，周围生产井快速见水.甚至会堵死低渗层，形成水锁现象.统计分析L1油藏连通井数对于注水井吸水能力的影响，发现与注水井射孔层段相连通的油井数越多，则注水井的吸水量越大，故若注水井上下两个射孔层段所连通井数相差较大的话，则易造成注水井吸水剖面不均匀的现象.因此，本文提出用连通井数的变异系数来判断其对分层注水的影响，可以认为连通井数的不均匀性越强，则越应进行分注.

1.4 连通井距

连通井距是指与注水井射孔层段相连通的油井与注水井的平均距离.对致密油藏来说，若井距过大，则由于压力传播慢，导致注入水很难扩散，影响注水井的吸水能力，周围的生产井长期不受效；而井距过小则容易造成油井过早水淹的状况，且在经济上不合算.因此当注水井上下两个射孔层段的井距相差较大时，应进行分层注水，即可以用连通井距的变异系数作为判断注水井是否需要分注的重要参数之一，认为连通井距的均匀性越差，注水井越应分注.

2 隶属函数的确定及单因素决策

隶属函数是用于表征单因素分布对于评判集分布规律的数学函数，并应用决策因子来表征某一因素的评判值，再根据各因素的权重系数与该决策因子的乘积，我们便可求得多因素的决策因子，该法即为模糊判别法[10,11].我们根据L1井区的实际情况选择隶属函数.

统计与分析了L1油藏实际吸水剖面，发现渗透率级差的隶属函数应属于升岭形分布，即级差越大，渗透率非均质性越强，注水井越应进行分注，公式如下[11]：

(1)

式(1)中：a1,a2为单项指标(渗透率极差)的最小值和最大值；μ(u)为隶属函数.

根据实际情况，简化上述公式并计算渗透率级差K(i)，渗透率决策因子FK(i)：

(2)

式(2)中：i为井数，i=1,2,3…,n；K(i)为第i口井的渗透率级差；FK(i)为第i口井的渗透率级差决策因子；n为总井数；Kmax=Max(K(1),K(2)…K(n))；Kmin=Min(K(1),K(2)…K(n)).

按上述公式即可计算出渗透率级差的单因素决策因子，以便在多因素综合分析中使用.

根据L1油藏实际吸水剖面资料的统计和分析，判断出有效厚度的隶属函数应属于升半梯形，即有效厚度越大，注水井越应分注，公式如下[11]：

(3)

式(3)中：a1,a2为单项指标(有效厚度)的最小值和最大值.

根据实际情况，简化上述公式并计算有效厚度H(i)、有效厚度决策因子FH(i)：

(4)

式(4)中：H(i)为第i口井的渗透率级差；FH(i)为第i口井的有效厚度决策因子；Hmax=Max(H(1),H(2)…H(n))；Hmin=Min(H(1),H(2)…H(n)).

按上述公式即可计算出有效厚度的单因素决策因子，以便在多因素综合分析中使用.

同样判断出连通井数变异系数和连通井距变异系数的隶属函数也应属于升半梯形，连通井数变异系数决策因子(HW)和连通井距变异系数决策因子(FL)的计算方法与公式(4)相同.这两个参数不均匀性越强，注水井越应分注.

3 权重系数的确定

在求解多因素决策的问题中，权重计算的准确性将严重影响最后所计算出的决策因子的准确性和可靠性.目前求解权重系数应用较为广泛的方法是层次分析法[12]，该方法系统、灵活、且便于理解和计算.层次分析方法又主要包括了四种方法：求和法、方根法、特征向量法以及最小二乘法.这里我们主要应用求和法和方根法来计算上述四个因素的权重.

3.1 基于求和法的权重计算

(1)根据实际油藏数据的统计和分析，分析了各决策因素对判断集的影响方式及程度，故可引用数字1～9及其倒数构成的模糊判断矩阵来代替语言判断，故可设判断矩阵如下：

(5)

式(5)中：

其中aij的取值可以根据表1来确定：

表1 模糊判断矩阵判断值定义

(2)确定了模糊判断矩阵之后，即可按列对其做归一化处理，得到Q=(qij)n*n；

(3)将矩阵Q=(qij)n*n按行相加，得到模糊向量C=(c1,c2,…,cn)T；

(4)将向量C=(c1,c2,…,cn)T进行归一化处理，即可得到各决策因素的权重系数W.

3.2 基于方根法的权重计算

(1)与求和法相似，先确定模糊判断矩阵；

(2)对模糊判断矩阵按列进行归一化处理，得到Q=(qij)n*n；

(3)将矩阵Q=(qij)n*n按行求积并开n次方，得到模糊向量C=(c1,c2,…,cn)T；

(4)将向量C=(c1,c2,…,cn)T进行归一化处理，即可得到各决策因素的权重系数W.

4 多因素综合判断

通过单因素分析的结果可靠性较低，无法准确判断一口注水井是否需要分注，因此需进行多因素综合判断，分析在多种因素的共同作用下，注水井是否需分注开发.

综上所述，单级综合评判法的具体步骤如下：

(1)取定评判对象；

(2)确定评语集V={v1,v2,…,vn}，即注水井是否分注；

(3)确定因素集U={u1,u2,…,un}，即上述分析的四个因素；

(4)依据各因素确定其决策因子ri，进而构成R=(rij)n*n，即可应用上述所选择的隶属函数来计算；

(5)确定权重集A={a1,a2,…,an}，即可应用上述两种权重计算方法来确定；

(6)作模糊变换B=A*R，求得评价结果B.

5 实例分析

5.1 确定因素指标及其决策因子

以L1油藏15口注水井为例，根据上述方法，计算得到的渗透率极差、厚度、连通井数变异系数、连通井距变异系数共4个参数数值如表2所示.由于每个参数的取值精度不同，表2中每个参数精度有差异，其中连通井数变异系数和连通井距变异系数精确到4位小数.

表2 L1油藏15口注水井影响因素指标表

根据公式(1)至公式(4)计算表2中15口井关于这4个因素的决策因子，列入如表3所示.

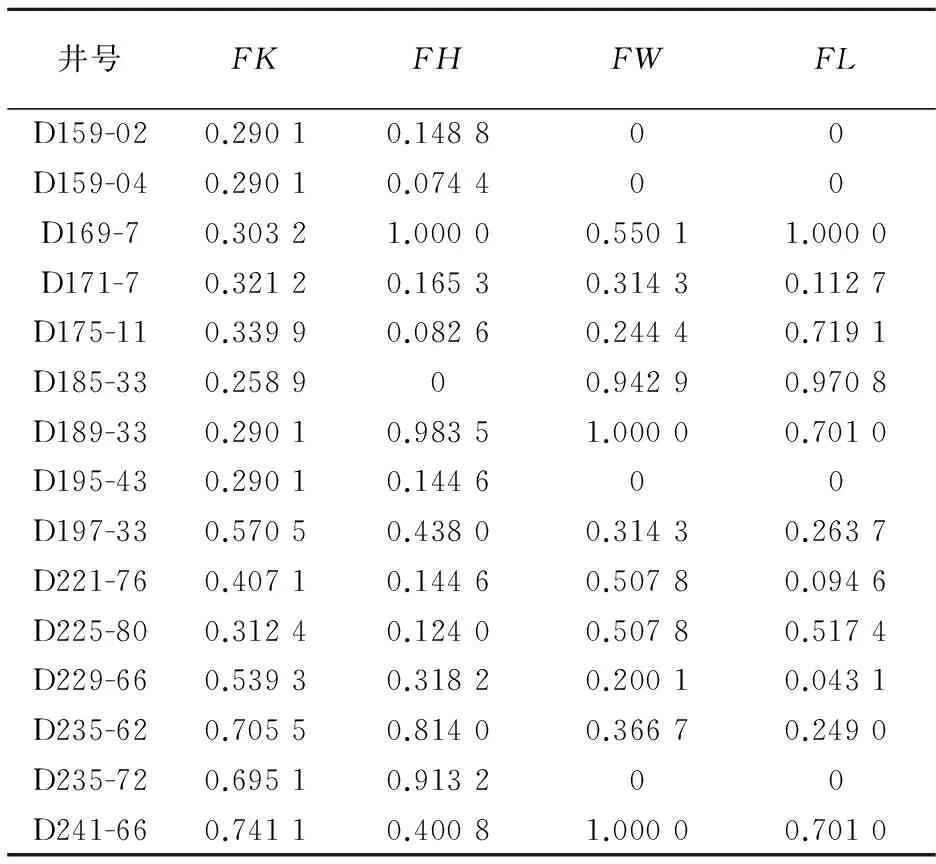
表3 L1油藏15口注水井的4个决策因子

5.2 计算权重系数

计算出每个单因素的决策因子后，还需计算出每个因素的权重系数，方可判断其是否可以进行分注.分别应用上面介绍的求和法和方根法计算这4个因素的权重系数.

(1)确定其模糊判断矩阵为：

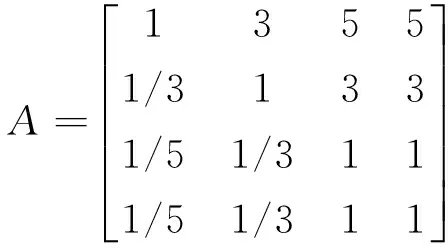
(2)应用求和法计算权重系数：

W=(0.554 9，0.251 6，0.096 7，0.096 7)T

(3)应用方根法计算权重系数：

W=(0.557 8，0.249 5，0.096 3，0.096 3)T

从上面两种方法的结果可以看到，应用求和法和方根法计算的结果较为接近.且所选择的模糊判断矩阵满足一致性检验.故我们认为模糊判断矩阵较为准确，其所求得的权重系数也较为准确.

5.3 多因素综合决策因子的计算

由表4可以看出，该油藏平均综合决策因子为0.404 5，而在这15口井中有6口井大于该平均值，分别为D169-7、D189-33、D197-33、D235-62、D235-72、D241-66，故我们可以判断这6口注水井需分注，而剩下的9口井不需分注，这与现场实际的分注结果相吻合，且分注后开采效果更好.

表4 多因素综合决策因子数据表

6 结论

(1)首次提出油水井连通井数和连通井距作为致密油藏注水井分注的关键判别参数.

(2)以L1油藏实际数据为依据，确定了渗透率级差、有效厚度、连通井数变异系数以及连通井距变异系数的隶属函数及单因素决策因子.

(3)应用求和法和方根法计算4个因素的权重系数，从而建立一套判别分注井的模糊数学方法.

(4)应用模糊判别法判别L1油藏15口注水井中有6口需分注，这一结果与该区实际情况相吻合，证明该法是可行的.

[1] 冯其红，王 波，王 相,等.高含水油藏细分注水层段组合优选方法研究[J].西南石油大学学报(自然科学版)，2016,38(2):103-108.

[2] 谢 华，王 凤.细分注水方法的研究[J].油气田地面工程,2007,26(2):8-9.

[3] 周 望，李 智，谢朝阳.大庆油田分层开采技术的发展与应用[J].大庆石油地质与开发,1998,17(1):36-39.

[4] 黄伏生，赵永胜.高含水期砂岩油田细分注水最佳分级模拟研究[J].大庆石油地质与开发,1998,17(2):30-31.

[5] 李 慧，王家春，李本生.数值模拟分层注水技术研究[J].石油工业计算机应用，2005,13(3):16-18.

[6] 冯其红，陈月明，姜汉桥，等.模糊数学在区块整体调剖选井中的应用[J].石油勘探与开发，1998，25(3):76-79.

[7] 程顶胜，刘 松，吴培红.塔里木盆地石炭系生烃潜力的模糊数学综合评价[J].石油学报，2000,21(1):34-39.

[8] 周 琦，姜汉桥，李志刚，等.利用吸水剖面测试资料优化分层注水措施[J].油气井测试，2009,18(3):11-12.

[9] 刘 凯，李家军，杨 莉.隶属函数确定方法模糊决策测度及改善[J].陕西工学院学报，2005，21(1):68-71.

[10] 汪培庄,李洪兴.模糊系统理论与模糊计算机[M].北京:科学出版社,1996:78-92.

[11] 崔 杰，党耀国，刘思峰.基于灰色关联度求解指标权重的改进方法[J].中国管理科学，2008,16(5):141-145.

[12] 邓 雪，李家铭，曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识，2012,42(7):93-99.

【责任编辑：陈 佳】

Layered injection wells distinguished by fuzzy mathematics method in tight reservoirs

XU Yang1, ZHANG Tao1, LIANG Cong2, CHENG Shi-qing2*, WANG Bin3

(1.Zhanjiang Branch, China France Bohai Geoservices Co., Ltd., Zhanjiang 524057, China; 2.MOE Key Laboratory of Petroleum Engineering, China University of Petroleum (Beijing), Beijing 102249, China; 3.Exploration and Development Research Institute, PetroChina Changqing Oilfield Company, Xi′an 710021, China)

Connected well number and spacing are proposed to characterize the water absorbing capacity of development factors in tight reservoirs,with which we combine permeability ratio and effective thickness,and fuzzy mathematics method are used to select the wells for subdivision water injection.We determine the decision factors by calculating the Membership functions of the permeability ratio,the effective thickness,the coefficient of variation of numbers of wells connected and connected well space and combining with the weight coefficient calculation method,such as the square root method and the sum method,to establish an effective method for determining the layered injection wells.We apply the method to L1 reservoir and the result shows that our method is reasonable.

tight reservoir; layered water injection; water absorbing capacity; fuzzy mathematics method; weight coefficient

2016-12-27

国家自然科学基金项目(41472113)； 低渗透油气田勘探开发国家工程实验室科研项目(2015)

徐 杨(1982-)，男，重庆人，工程师，研究方向：油气井测试

程时清(1963-)，男，湖北大冶人，教授,博士，研究方向：低渗透油藏开发及复杂油藏试井，chengsq973@163.com

2096-398X(2017)03-0111-05

TE319

A