思辨“探究”教学体悟“发现”本真

■韩新正

思辨“探究”教学体悟“发现”本真

■韩新正

传统教学过于强调知识传授，探究式教学提倡学生自主探究、主动建构，我们既需要教师能真正指导学生进行自主探究，又需要教师的讲解，以促进学生有意义地接受。

探究教学问题对策

探究式教学，又称发现学习，是布鲁纳在《教育过程》中提出来的。这种方法要求学生在教师的认真指导下，像科学家发现真理那样，通过自己的探索和学习“发现”事物变化的因果关系及其内在联系，形成概念，获得原理。《义务教育数学课程标准（2011年版）》在课程基本理念中指出，学生学习应当是一个生动活泼的、主动的和富有个性的过程。除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式。显然，探究式教学重视培养学生的自学能力，发展学生的创造性思维，引导学生学会学习，因此，教师在课堂实践中会广泛使用探究式教学方法，但由于一些教师对“发现教学”的认识不到位，虚假探究导致课堂效率低下的现象屡见不鲜。

一、探究式教学中常见问题及对策

1.有些课题不适合用探究式教学方法。

案例1：在“勾股定理”的第一节教学中，有如下教学设计。

活动1课前调研，引出问题。

问题1：我们之前学习过哪些三角形？

问题2：按角分类，大家认为比较特殊的三角形是哪些？原因是什么？

问题3：直角三角形的角度很特殊，那它的边在数量上会不会也有特殊的关系呢？

活动2动手作图，探究关系。

（1）学生作图，发现规律。请同学们动手画一个任意的直角三角形，并测量其三边的长度，计算各长度之间的关系，互相交流。

（2）各小组的学生展示所得数据及猜想。教师写出猜想：在一个直角三角形中，两条直角边长度的平方和等于斜边长度的平方。

（3）几何画板演示。学生拖动直角三角形的顶点，使其大小、形状发生变化，不变的是直角，观察上述猜想中的三边关系。

活动3实践验证，得出定理。

分析：粗看这一教学过程，学生在教师的引导下，通过小组合作、共同探究、认真思考得出勾股定理。但在实际教学中，这却是一个很难完成的探究过程。因为学生画图、测量时无法保证图形、数据的准确性，这就无法为发现规律提供保证，此外，大部分学生根据测量的数据，不会轻易猜想出各边长的平方之间的关系。

对策：对“勾股定理”的教学大致可分为两种类型，一种是直接告知学生勾股定理的内容，然后重点让学生去证明这个定理。因为勾股定理的发现具有偶然性，如果对数字不是极其敏感，一般人很难直接猜想到定理的结论。另一种是从普通三角形三边的关系的不确定性引导学生探究，告知学生从面积的角度去研究直角三角形三边的关系。江苏省特级教师于新华老师对此给出了很好的尝试：

（1）教师先展示边长为3和4，夹角为任意角的三角形，要求学生求出第三边的长。经探索，学生无法求出。

（2）如果边长为3和4的两边夹角是直角，第三边的长确定吗？经探索，学生发现可以确定。

（3）如何求出第三边的长？我们不妨把该直角三角形放到带有网格的背景中去，借助网格来探求方法。

（4）教师启发引导，要求边长的大小，可以求边长的平方，即求以此边为边长的正方形的面积，然后导入面积的求法。

（5）从特殊到一般，在初步探求出“勾三股四弦五”后，进一步借助前述方法探索一般直角三角形的三边关系，得出勾股定理。

2.少了数学思维的探究只是数学游戏。

案例2：在“过直线外一点作已知直线的垂线”的教学中，有如下教学设计。

例：已知，直线AB和AB外一点C（如图1）。用直尺和圆规作AB的垂线，使它经过点C。

图1

探究过程：

（1）任意取一点K，使点K和点C在AB的两旁；

（2）以点C为圆心，CK长为半径作弧，交AB于点D和点E；

（3）分别以点D和点E为圆心，大于DE的长为半径作弧，两弧相交于点F；

（4）作直线CF，直线CF就是所求作的垂线。

在探究过程中，教师每写出一步作法，都会问学生为什么，引导学生思考，然后教师会跟学生讲作法的意义，让学生明白为什么直线CF就是所求垂线。最后学生按照教师的要求，重新画一次图以作巩固。

分析：数学探究是为发现、提出、验证数学结论或解决数学问题而进行的观察、猜想、验证、推理、运算等一系列操作与思维活动，因此，数学探究的根本是数学思维。在程序性流程指引下的操作探究，如果缺少数学思维的成分，就是一个数学游戏。本例的探究过程就只是一个操作过程而已，师生看似在探究，其实学生只是“作图”的机械执行者，其间并没有主动的思维活动。

对策：经过直线外一点作这条直线的垂线（尺规作图），我们把问题转化为作某条线段的垂直平分线，于是自然想到在直线AB上寻找一条线段，使得该线段的垂直平分线经过点C。可做如下设计。

师：如图2，已知，直线AB和AB外一点C。求作AB的垂线，使它经过点C。方法不限，请大家自由思考。

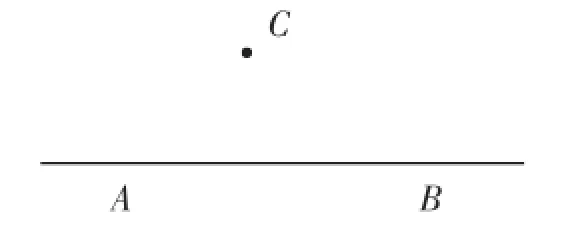
图2

预设：（1）把直线AB对折，使折痕经过点C，折痕所在直线就是AB的垂线；（2）用量角器直接量出∠CDB即可，如图3；（3）使直角三角尺的一条直角边与AB重合，另一条直角边经过点C，过点C的直线即为AB的垂线。

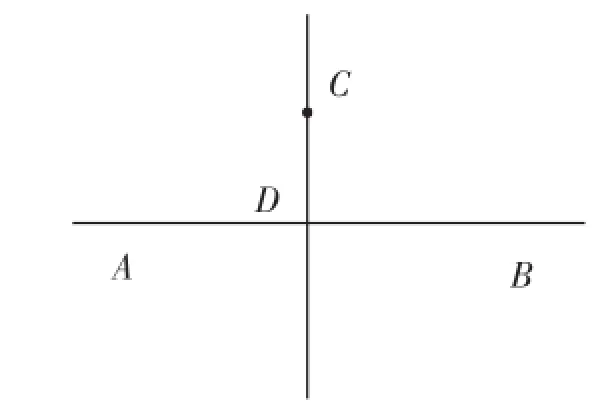
图3

师：如果用尺规作图，该如何思考呢？从上面的3种方法中能否找到可以借鉴的作法？

显然，从上面3种作法中找不到可以借鉴的经验，这时教师的引导显得非常重要。

师：过点C作直线AB的垂线比较困难，结合我们所讲的内容（线段垂直平分线），我们是否可以做一个转化，在直线AB上找到一条线段DE，使得线段DE的垂直平分线经过点C？如果找到这样的线段DE，则必有CD=CE。那么如何作出CD=CE呢？（这一步可以留出时间让学生思考、讨论）

预设：以点C为圆心，以足够长为半径作弧，交直线AB于点D、E，如图1。

师：半径有要求吗？

预设：必须保证所画的弧和直线AB有交点。

师：接下来怎么办？

预设：既然已经找到线段DE，下面就是作DE的垂直平分线了，作法：分别以点D和点E为圆心，大于DE的长为半径作弧，两弧相交于点F，作直线CF，直线CF就是所求垂线。

在这样的探究过程中，学生不仅能参与作图，而且还能主动思考。这种探究过程就不再是一个简单的数学游戏了。

3.探究缺少计划，忽视合作与交流。

案例3：抛硬币——探究硬币正面朝上的概率。

教师预先让同桌的两名同学准备1枚1元的硬币，上课后，1个人抛硬币，1个人记录，每桌抛硬币50次，再让每桌同学计算正面朝上的频率，然后分析每桌抛硬币的频率，得出各组的频率都在0.5左右波动，因此得出0.5就是正面朝上的概率。

分析：这是一个看似完整的探究过程，有过程，有结果，有学生参与。但综合观察整个过程会发现，教师课前缺少计划，对各组得出的数据不能充分利用，同桌间的合作比较单调，教师对合作的理解比较狭隘（仅理解为同桌活动，其实对各组得出数据的充分利用也是合作）。

对策：（1）制定计划，课堂上每桌抛硬币50次，对每桌的数据进行统计，让学生感受频率的概念；

（2）对每桌数据按表1进行统计，让学生感受随着试验次数的增加，频率越来越稳定，小组合作不仅在同桌之间，可逐步扩大到全班同学；

（3）讨论为什么随着试验次数的增加，频率会越来越稳定，引导学生感受这个稳定的数就是概率，这里可让学生畅所欲言，因为不同的人对此有不同的感受；

（4）教师对活动过程进行评价，应特别强调虽然每组只抛了50次，但全班合起来就有一千多次，如果每组再增加试验次数，试验的次数就越多，也就越能说明频率和概率的关系；

（5）教师介绍硬币正面朝上概率的有趣故事。

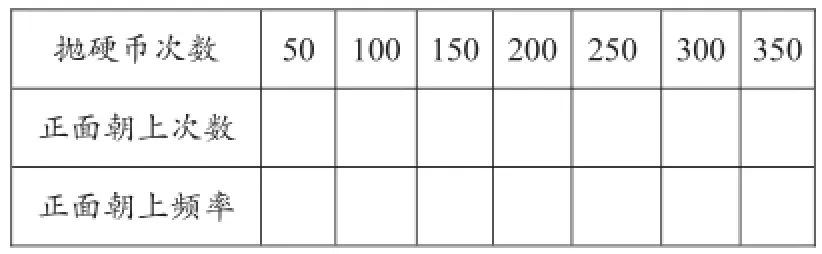
表1抛硬币的数据

二、对探究式教学的思考

1.让学生掌握科学探究的方法。

教学中教师要走出一个误区，不要以为只要学生参与了活动就是探究。探究是在教师的指导下，学生通过操作、实验等方法，在思维的参与下发现事物发展规律的过程，所以，教师要从4个方面促使学生进行发现：

（1）教师与学生合作；

（2）学生参与知识结构的形成；

（3）让学生了解各种可供选择的方法和不同的观点；

（4）学生有发表自己意见的机会。

案例2中教师直接告知学生画垂线的方式，尽管事后学生也能理解为什么这样画，但缺少运用线段垂直平分线的知识去探究的过程，学生不知道还能运用所学知识解决实际问题，不能形成科学探究的习惯。案例3缺少了把每组的试验次数累加的过程，学生感受不到“随着试验次数的增加，频率越来越稳定”这一事实，更感受不到合作带来的学习便利。所以让学生掌握科学探究的方法是学生学会学习、学会发现的前提和保证。

2.处理好学生自主探究和教师讲授的关系。

《义务教育数学课程标准（2011年版）》指出，教师要发挥主导作用，处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学探究活动经验。为创新课堂教学模式，不少地方严格限制教师讲授时间，主张学生是课堂的主人，把时间和学习主动权还给学生，甚至严格规定教师讲授时间不超过5分钟。其实这是对探究式教学的误解，探究式教学虽然在提高学生发现问题、分析问题能力方面有优势，但其缺点也是明显的。

首先是时间成本，学生每天学习数学的时间是有限的，在有限时间内学习那么多知识，并达到相应技能，全靠探究式教学是难以实现的。

其次，对学生能力的要求较高，在教学中如果无视学生的个别差异，广泛使用发现法，只会给思维缓慢、胆怯怕羞或学习缺乏信心的学生带来更多的自卑、恐惧和厌恶学习的心理。

再次，不是所有的内容都适合探究，前人在发现有关定理、结论时，可能经历了几十年甚至数百年，一节课要完成探究、发现，其难度可想而知，案例1中勾股定理的发现就是“天才的顿悟”，想把这一伟大的发现在一节课上让学生自主探究出来，显然做不到，所以我们需要教师的讲授。美国心理学家奥苏贝尔认为，对学生来说，获得知识最经济、最有效的方法是有意义的言语接受学习。所以案例1中教师在引导学生发现直角三角形三边间的关系时，可以人为削减探究难度，引导学生从三边长的平方关系进行探究，而从a2+b2=c2这样的“式结构”引导学生联想到特殊三角形面积的“形结构”，便需要教师进行言语引导，甚至要浓墨重彩地讲解。

3.处理好探究活动和思维的关系。

布鲁纳认为，所谓发现并不仅仅是指寻求人类尚未知晓的新事物，它还包括用自己的头脑亲自去获得知识的一切方法。显然，探究式教学主要是指后者，而后者的核心是“用自己的头脑”，所以探究式教学的核心指向是“思维”，没有思维参与的探究就是一个数学游戏。

例如案例2，如果学生对照作图顺序，按部就班地作出已知直线的垂线，他们仅仅是作图程序的机械执行者，整个过程没有思维参与，这一过程就失去了探究的价值，学生通过学习画图外，数学思考能力、基本活动经验积累都没有得到锻炼。

再比如案例3中的抛硬币活动，如果没有课前精心计划，课中巧妙引导，本节课就是一个单纯的抛硬币游戏，如果有了思维的参与，学生便可以有如下收获：（1）知道频率的概念；（2）感受到随着试验次数的增加，频率越来越稳定，初步知道如何用频率估计概率；（3）真正理解合作的重要性，抛硬币试验几千次，靠一个人、一个组是很难完成的，只有分工协作才能达成目标；（4）积累活动经验，学生会认识到抛硬币出现正面朝上的概率不是想当然的结果，而是实实在在的试验结果，在科学实验中不能犯亚里士多德的“重的物体总比轻的物体下降速度快”这样想当然的错误。

总之，探究式教学提倡学生自主探究、主动建构，重视发挥学生主观能动性和创新意识培养，讲解主要说明新旧知识的关系，填补学生原有经验与新知识之间的缝隙，剖析新知识自身各要素之间的联系。只有充分认识学生自主探究和教师讲解的关系，我们的教学才能事半功倍，更有利于学生的一般发展。教师只有将两者结合起来，不断丰富教学手段，才能培养出真正的创新人才。

（作者为江苏省泰州市海陵学校教师）