寻找生活中的数学美 成就美丽的数学课堂

范春玲

摘 要：面对数字的形式美，学生能有直观的感受，而要探索其中隐含的数学规律的奥秘，则需要教师对教学内容进行选择、重组，与解决生活中的实际问题相联系，让学生在数学发现中得到感悟，体悟到数学思维训练的美妙，进一步激发学生的情感体验，提高对数学美的欣赏水平，享受数学的美带来的愉悦。

关键词：生活；美；数学

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2017）02-0092-02

Abstract： In the face of the beauty of form numbers， students can have intuitive feelings， and to explore the mysteries of the underlying mathematical laws， it is necessary for teachers to choose， reorganize teaching content， link to solving practical problems in life， and let the students get insights in mathematical discovery and realize that the training of mathematical thinking is beautiful. They should further stimulate the students' emotional experience， improve their level of appreciation of the beauty of mathematics， and help them enjoy the pleasure of beauty.

Keywords： life； beauty； mathematics

大家都知道，数学来源于生活，我们的数学课堂，要引导孩子畅游“数”的海洋，更应该创设情境，再现生活中的数学美。正如徐利治教授指出的：“学习材料的兴趣和美学价值乃是学习的最佳刺激，强烈的心智活动所带来的美的愉悦和享受是推动学习的最好动力。”仅仅就数学内容进行教学，这样的课堂是很单调的，当我们将数学内容融入到生活情境当中，引导孩子们善于发现、寻找生活中的数学美，这样，数学的内在美才能焕发出动人的光彩。

一、在数字形式美的感受中，获得探索数学规律的愉悦

通过对数学美的不断学习，学生可以认识到数学无尽的魅力，在生活中，随处可以看到数学在其中起的作用。甚至可以说，因为数学让我们的生活更美好，世界更美丽。

生活中数学无处不在，而数字却是最常见的。哈克斯普特认为，数学是“美学欣赏的源泉和娱乐的形式”，并且非常重视培养孩子们的数学思维，并把它看作“人类智力成就的巅峰之一”。了解数字和数字运算，为孩子们超越数学的纯功利性应用提供可能，进而使他们积极主动去探索那些引人入胜的、能引导逻辑思维和数学推理的数字模式，以及数字联系。在观察呈现数字和计算程序之间关系的模式和联系时，所有孩子都能从数学思维中获得满足感，教师会意识到个体的“发现”能培养他们积极的学习动机。

例如：当基于简单计算的观察活动能引导他们预测结果并争论所使用的方法，那么，这些预测和争论正是激发思维力量的动力。我们对奇数连续相加，就会发现其结果是某一个数的平方：

1+3=2×2

1+3+5=3×3

1+3+5+7=4×4

1+3+5+7+9=5×5

1+3+5+7+9+11=6×6

……

在分析这一数字模式的时候，教师可以先让孩子们在不计算的前提下，预测前9个奇数的和，前10个奇数的和，或者前1000个奇数的和，然后向孩子们提出问题，为什么会存在这样的数字关系呢？

有时候，我们只需要通过计算，再对不同数字进行组合，就能得到一些非常奇妙的排列，令人拍案叫绝，回味无穷：3×4=12，33×34=1122，333×334=111222，3333×3334=11112222……

又如： 1×1=1

11×11=121

111×111=12321

1111×1111=1234321

11111×11111=123454321

111111×111111=12345654321

1111111×1111111=1234567654321

11111111×11111111=123456787654321

111111111×111111111=12345678987654321

在数学学习中，适当地呈现这些有趣的问题，会引导孩子们进入数字的魔幻世界，在那里，他们会不断地发现富于逻辑性的解释，并不断探索到激动人心的数字事实。

二、解决生活中的实际问题，体会数学思维方法的美妙

有一位教师在执教《烙饼的策略》时，花了心思去设计教学过程。首先，课前导入呈现一个富有生活气息的问题情境：“煮熟一个鸡蛋需要5分钟，煮熟5个鸡蛋需要多少分钟？”立马有学生上当：“25分钟。”“25分钟吗？太长了。一起煮只需要──”“5分钟！”孩子们都笑了。

在轻松愉悦的氛围中，教师揭示课题《烙饼的策略》，并依次出示以下问题：

1. 一張饼两面都要烙，烙一面需要3分钟，烙一张饼需要多少分钟？3×2=6（分钟）

烙2张饼呢？6×2=12（分钟）烙3张饼呢？6×3=18（分钟）

2. 一张饼两面都要烙，烙一面需要3分钟，每次可以同时烙两张饼。现在要烙两张饼，你可以怎样烙？

学生讨论后汇报：1.两张饼同时烙，只需6分钟；2.一张一张轮流烙，需要12分钟。

“你喜欢哪一种方法？为什么？”“第二种。节省时间、更快吃上饼。”在学生理解到“同时烙”比“轮流烙”更省时的时候，教师应当告诉孩子们，在数学中，可以把更好的方法称之为“优化”。

根据前面的规律解决问题：烙4张饼需要多少分钟？烙8张饼呢？10张呢？12张呢？100张呢？

指名回答：烙100张饼需要300分钟，列式：100÷2×6=300（分钟）。

生：其实只要100×3就可以了。（肯定学生的回答）

继续抛出问题：烙3张饼需要几分钟？让学生猜：9分钟、12分钟、18分钟……三种方法，差别为什么会这么大？

利用学具进行演示、讨论并展示，让学生明白除了“轮流烙”、“同时烙”，还可以“交替烙”：1. 烙两张饼的A面；2. 烙第一张饼的B面和第三张饼的A面；3. 烙第二张饼的B面和第三张饼的B面。表述清晰，学生易于理解。

进一步“优化”：在实际生活中，我们可以把“同时烙”和“交替烙”结合起来。例如：“美味餐厅”有2名厨师、3桌客人，每桌客人点了3个菜。怎样才能让客人更快吃上菜？

整个课堂，教师巧设层层“陷阱”，学生兴趣盎然，充满着生活气息。正如吴正宪老师所说，数学，处处充满着美，不过，这种潜在的、隐含的美，是不可能自发起作用的，作为教师，我们应该努力挖掘她的美，渲染她的美，真诚地牵起孩子的手，与他们一道跃进这美的海洋，一起去感受、领略数学的美，帮助他们揭示数学知识内涵的美，培养他们对数学学习的浓厚兴趣，激发他们探索数学奥秘的强烈愿望。

三、数学发现中的美学感悟，激起学生对数学美的欣赏

因为数学美，人们对学习数学的激情只增不减；因为数学美，启发着人们探求真理的思路；寓美于教，能激发学生的学习兴趣。数学，有智育的功能，更有美育的功能。数学美深深地感染着人们的心灵，激起人们对她的欣赏。

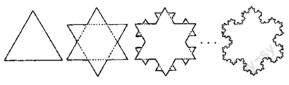
冬季来临，很少有孩子能拒绝滚雪球、打雪仗的诱惑，那晶莹剔透的雪花，引发了多少诗意的赞叹。那么，雪花究竟是什么形状呢？我们可以告诉孩子们，要回答这个问题，离不开数学。1904年，科赫（瑞典数学家）找到了描述雪花形状的方法：首先，我们需要画一个等边三角形，然后，在原三角形的三條边上各放一个小等边三角形（边长为原来三角形边长的三分之一），这时，我们得到了一个六角星；接下来，我们要做的就是重复上述的方法，把每个角上的小等边三角形变成一个小六角星……这样，一直进行下去，就得到了雪花的近似形状。

怎么样？是不是感觉到数学和艺术一样，有自己的美学特征，能够起着陶冶情操，完善思维品质的作用呢？

在我们的基础教育中，数学占有相当大的份量，同时，也是我们中华文化中极为重要的组成部分。作为一线教育工作者的我们，应该有意识地去引导孩子们发现“数学美”、欣赏“数学美”，从而提高他们的数学素养。

孩子们的数学学习来源于生活，来源于他们对生活的感悟，正是这份感悟，成就了美丽的数学课堂；孩子们拥有的丰富的想象力，孩子们天然的童真童趣，孩子们纯真的笑容，成就了美丽的数学课堂。我们应该和孩子们一起，共同融入这美的意境，去尽情领略、享受数学中的美。

参考文献

[1]中华人民共和国教育部.数学课程标准[M].北京师范大学出版社，2001.

[2]张丹.小学数学教学策略[M].北京师范大学出版社，2010.

[3]王冬娟.深度探究：小学数学课程教学践行与反思[M].东北师范大学出版社，2011.

[4]李士 ，张晓霞，金成梁.小学数学教学案例研究[M].高等教育出版社，2010.

[5]吴正宪.吴正宪与小学数学[M].北京师范大学出版社，2006.

[6][英]朱莉娅·安吉莱瑞.如何培养学生的数感[M]徐文彬译.北京师范大学出版社，2007.