基于时间Petri网流通加工系统的建模研究
张春娜


摘 要: 以某配送中心的流通加工系统为例,考虑流通加工系统作业的离散性和时间性因素,采用时间Petri网建模的方法,构建该系统的时间Petri网模型,并运用其化简规则对模型进行化简分析,得出该系统作业的时间区间范围。该方法为配送中心流通加工系统的建模提供了有益的参考。
关键词: 流通加工; 时间Petri网; 建模
中图分类号: TP 393 文献标志码: A 文章编号: 1671-2153(2017)04-0094-03
0 引 言
流通加工是现代物流配送中心作业活动中重要的一环,它能够根据客户的要求完成物品在流通领域的加工任务,为消费者提供重要的增值服务。在流通加工过程中,如何合理地组织人力、物力,加速商品在仓库中的周转,取得最大的经济效益是配送中心组织管理的首要问题。
目前多采用离散事件动态建模(DEDS)的方法对此类问题进行分析研究。鉴于Petri网模型是一种图形分析和数学分析兼而有之的建模工具,所以本文重点讨论如何采用时间Petri网模型,对某农副产品批零市场的流通加工作业流程进行建模研究。
1 系统时间Petri网模型的建立
为了使所建的模型更具有代表性和可研究性,本文以某批次农副产品一次订单加工过程为例,对其进行建模研究。根据订单的要求,首先应对农副产品的质量进行检测,主要包含检测蔬菜、果品类的药物残留,检测肉类、鱼类是否含有有毒有害物质等,对于检测结果不合格的产品,按规定处理或者就地销毁。对于检测合格的产品分为两类,一类只需要进行清洗等简单的加工操作,这类在文中称为A类产品,对其进行的加工称为初加工。另一类除清洗外,还需要进一步的加工,如去皮、切块等,这类在文中称为B类产品,对其的深加工称为二次加工。对于B类产品,在二次加工后需要进行质检,如果质检不合格,需要返工。质检合格的B类产品,需要和A类一同,组合打包、称重、贴标签,然后装箱搬运至待发货区。
根据产品作业过程,建立该流通加工系统的时间Petri网模型如图1所示。图1中,库所P1及其中的托肯表示产品到达配送中心,准备进入流通加工阶段,库所P2表示对农副产品的质量检测结束,库所P3和P4分别表示符合质检要求的产品和不符合质检要求的产品,库所P5和P6表示A类、B类产品分别到达待加工区,库所P7和P8分别表示对A类、B类产品的初加工完成,库所P9表示对B类产品的二次加工完成,库所P10表示对B类产品的二次加工质量验收完成,库所P11表示B类产品的二次加工质量不合格,库所P12表示B类产品等待再次二次加工,库所P13表示B类产品的二次加工质量合格,库所P14表示对A类、B类产品的组合打包完成,库所P15表示对A类、B类产品的称重、打标签完成,库所P16表示该流通加工作业完成,等待出库。
图1中出现的qB表示B类产品二次加工不合格,需要返回再加工的可能概率,在此取qB=1/10。该模型中各个变迁的含义如表1所示。
由表1可以看出,时间Petri网对变迁发生的时间区间有明确的界定。需要说明的是表中出现的瞬时变迁不代表此项作业在实际过程中不占用时间,只是相对与其他作业来说,此作业环节所用的时间非常短,可以忽略不计,所以用瞬时变迁来表示。
2 系统时间Petri网模型的简化与分析
时间Petri网由于引入了时间参数,能够更好地表达实际作业过程中与时间有紧密关系的作业内容。对于作业流程简单、节点数目较少的小规模的Petri网模型,可以直接对模型分析;而对于作业流程复杂、节点数目较多的Petri网模型,即使不产生状态空间爆炸问题,也会因为模型太复杂,细节太多,给分析带来困难。对于本例中建立的较为复杂的时间Petri网模型,首先有必要对其进行时间等效变换处理,得到较为简单的作业流程模型,然后再对其进行分析研究。
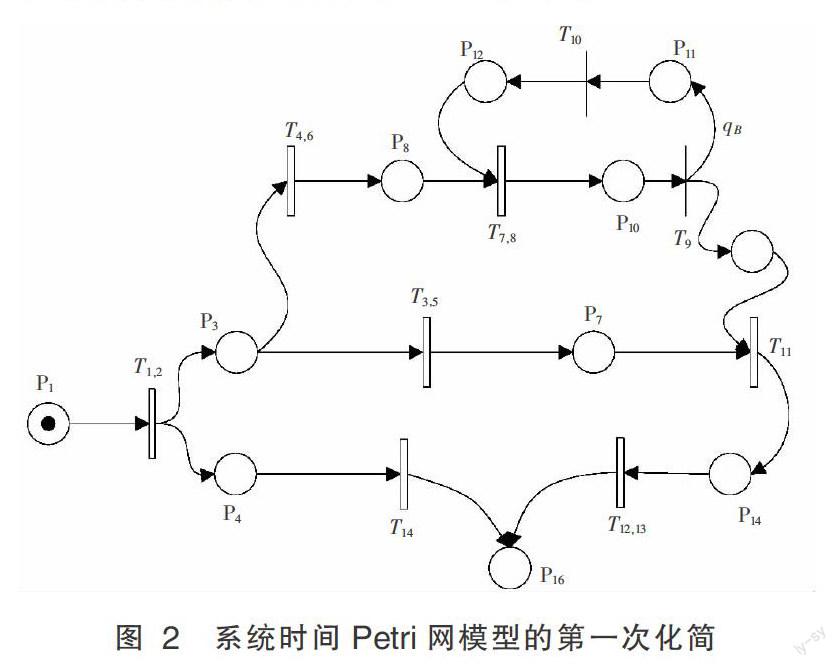
根据时间Petri网的化简規则对图1所示的流通加工模型进行化简。分析模型不难看出,模型中有多个顺序结构关系的变迁,采用时间Petri网的顺序结构关系化简规则对原模型进行第一次化简,化简后的模型如图2所示。
其等效化简过程中,时间变迁T1和T2化简后为[T1,2],[T1,2]=[T1+T2] =[15,25],按照同样的方法,分别将T3和T5整合为T3,5,T4和T6整合为T4,6,T7和T8整合为T7,8,T12和T13整合为T12,13,其等效的时间区间如表2所示。
对于图2所示的模型,仍然是比较复杂的,有必要对其进一步化简。由于时间变迁T4,6,T7,8,T9,T10之间是顺序加循环的关系,采用顺序结构关系化简规则和循环结构关系化简规则相结合的方法对其进行第二次等效化简,化简结果如图3所示。图3中,时间变迁的等效过程T7,8,T9,T10之间是循环的关系,采用循环结构关系化简规则,根据前文所述取qB=1/10,则有[T7,8,9,10]= [T7,8+T9+T10]/(1-qB)=[38.889,50],再次采用顺序结构关系化简规则,有[T4,6,7,8,9,10]=[T4,6+T7,8,9,10]=[83.889,105],等效变换关系结果如表3所示。
为了使模型更加简单,多次综合运用顺序结构关系化简规则、循环结构关系化简规则以及并行结构关系化简规则等,对图3所示的模型进行第三次等效化简,最终得到如图4所示的模型。
由第三次化简的最终模型可以看出,该批次的订单产品到达配送中心后,经检验对质量符合标准的产品进行加工作业,流通加工完成后等待发货;不符合标准的产品被移至退货区,等待后续处理。其时间变迁的等效关系及等效的时间区间范围如表4所示。
结合图4和表4可以看出,该批次的订单产品在配送中心的流通加工作业所用的时间区间,最短完成时间为138.889时间单位,最长完成时间为180时间单位;对于质检不合格的产品,通过此系统需要10到15时间单位。
3 结 论
通过采用时间Petri网对某农副产品配送中心的流通加工系统进行建模,并利用其化简规则对模型进行简化,得到某批次的订单产品在流通加工环节所耗费的时间区间范围。在不考虑特殊情况的条件下,此时间区间能够反映产品的流通加工效率。这种建模方法对现代物流配送中心管理及规划等问题的研究具有一定的借鉴作用。
参考文献:
[1] 潘理,杨勃. 基于时间Petri网的区间作业车间调度问题建模与分析[J]. 湖南理工学院学报(自然科学版),2016,29(1):33-36.
[2] 李玉民. 物流中心设施规划与运营系统建模方法研究[D]. 南京:东南大学,2004.
[3] HOLIDAY M A,VENON M K. A generalized timed Petri net model for performance analysis[J]. IEEE Trans. Software Eng.,1987,SE-13(12):1297-1310.
[4] 李诚,李爽,冯毅萍,等. 基于时间Petri网和启发式搜索的柔性制造系统调度算法[J]. 上海交通大学学报,2015,49(5):709-712.
[5] 张洪梅. 时间Petri网及其在仿真系统概念建模中的应用 [D]. 哈尔滨:哈尔滨工业大学,2014:15-24.

