基于模糊自抗扰的永磁同步电机转矩控制

远绍羊，张 政，熊志强，田新玲，任晓斌

(西安交通大学，西安 710049)

0 引 言

永磁同步电机(以下简称PMSM)因具有功率密度高、效率高、低速大扭矩及静音性等优点被广泛用作电动汽车驱动电机。目前，对于PMSM的研究主要集中在转速控制及位置控制，对于其转矩控制研究较少，而为满足驾驶员的驾驶习惯及转矩模式控制的直接性与快速性，对于PMSM转矩控制方法的研究尤为重要[1-2]。

PMSM是一个典型的强耦合、非线性、多变量的复杂时变系统。传统的PI控制过分依赖控制对象模型参数鲁棒性较差，在系统受到内部参数的变化以及外界扰动时，难以满足高性能、复杂工况的控制要求。因此，对于PMSM的非线性控制研究成为国内外学者研究的热点[3-6]。文献[7]将滑模变结构运用到了PMSM控制系统当中，增强了系统的鲁棒性，缩短了系统响应时间，但是由于滑模变结构所特有的“脉振”现象无法实现系统稳定性及控制精度的提高。文献[8]将自抗扰控制应用到了PMSM控制中减小系统的稳态误差，提高了控制精度，但是单一的自抗扰控制器参数较多，不便于实际操作与整定，实际应用受限。文献[9-10]采用了基于人工智能自适应调整PI参数的方法，但形式复杂、运算量大，难以满足实时性的要求。

本文综合考虑电动汽车驱动系统的应用需求，提出了一种模糊自抗扰转矩控制方法。将模糊控制运用在自抗扰控制器的设计中，在保持自抗扰控制器原有特点同时，充分结合了模糊控制自适应推理及在一定范围对参数的最佳估计能力，实现了对自抗扰控制器中非线性误差反馈控制率参数的最佳整定，减少调节参数的同时，也提高了控制系统自适应能力，实现了对PMSM非线性系统良好的转矩控制效果。

1 PMSM基本数学模型

PMSM在d-q轴坐标系下，为简化模型，忽略了磁路饱和并假设气隙磁势在空间作正弦分布[11]，通过坐标变换实现PMSM基本数学模型的解耦，将三相交流信号转化为旋转的两相直流信号，得到d-q轴坐标系的定子电压方程：

(1)

在d-q轴的磁链方程：

(2)

电磁转矩方程：

Te=p[ψfiq+(Ld-Lq)iqid]

(3)

式中：ud，uq分别为d，q轴电压；id，iq分别为d，q轴电流；Ld，Lq分别为d，q轴电感；Rs为定子电阻；θ为转子的电角度；ψf为永磁体的励磁磁链；ψd，ψq分别为d，q轴磁链分量；Te为电磁转矩；p为极对数。

2 PMSM模糊自抗扰转矩控制器设计

2.1 自抗扰控制基本原理

自抗扰控制(以下简称ADRC)是我国中科院研究员韩京清深入研究经典控制理论和现代控制理论各自精华与局限的基础上，利用大量计算机数字仿真实验，提出的具有原创性的实用控制技术，包括跟踪微分器(以下简称TD)、扩展状态观测器(以下简称ESO)以及非线性状态误差反馈控制(以下简称NLSEF)3个部分[12]。TD的作用是为给定目标信号安排快速无超调的过渡过程，得到平滑的输入信号及其微分信号。过渡过程使误差反馈增益的对象参数可用范围扩大，使得控制器的鲁棒性增强。ESO不依赖于控制对象的具体数学模型，能够观测控制对象的各状态变量、内外扰动。NLSEF根据状态变量的误差，计算控制对象输入量。其控制原理结构图如图1所示。

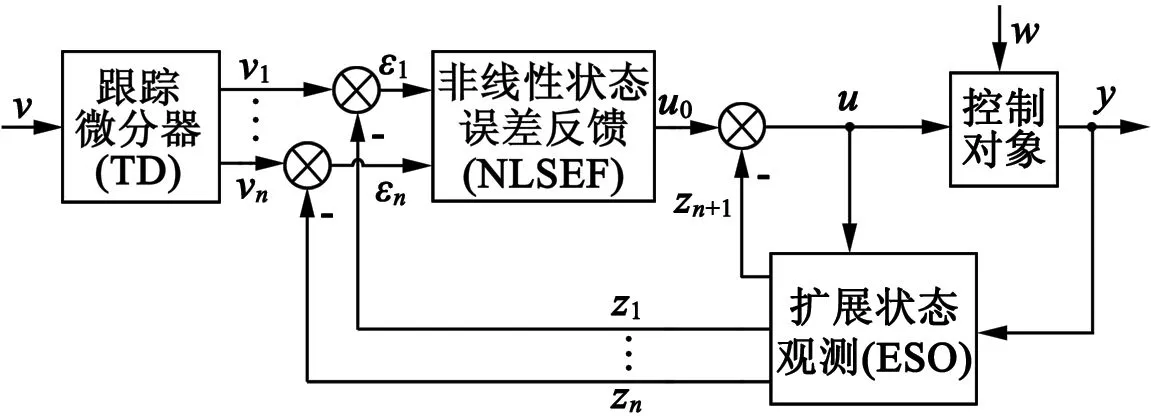
图1 自抗扰控制原理结构图

2.2 自抗扰控制器设计

当PMSM为表贴式结构时，有L=Ld=Lq，控制采用直轴电流id=0的控制方法，在减少励磁损耗的同时，实现最大转矩电流比控制，此时转矩与交轴电流iq成正比，直接对iq的幅值进行控制，即可实现对PMSM转矩的控制。具体公式如下：

Te=pψfiq

(4)

在同步坐标系下由式(1)和式(2)交轴电流环转矩控制下的一阶动态方程:

(5)

(6)

根据ADRC原理，自抗扰控制器的设计采用分离设计的原则，具体如下：

(1) 非线性跟踪微分器(TD)

利用快速最优综合控制函数构造的TD:

(7)

式中：iqref(n)是给定的交轴电流期望信号；v1(n),v2(n)根据期望转速信号安排出的过渡信号及其微分;h是采样周期;r和h0是可调整参数。

fhan(x1,x2,r,h)为快速最优综合控制函数，在实际应用的数字化控制系统中经常被采用，其表达式：

(8)

式中：r,h为可调整参数。

(2) 扩展状态观测器(ESO)

为了对内外扰动实时估计并补偿，设计二阶扩展观测器如下：

(9)

式中：h为采样周期，z1,z2分别是对式(9)中iq,wt的估计值，β1,β2,α1,α2,δ为可调整参数。为避免高频颤振现象的出现，采用在原点附近具有线性段的连续的幂次函数fal(·)最优控制函数，表达式：

(10)

式中：e为误差；α,δ为可调参数。

(3) 非线性状态误差反馈控制(NLSEF)

由观测器观测到了状态变量和扰动量后，采用NLSEF来实现扰动量的补偿及对被控对象控制量的输出，在交轴上设计的状态误差反馈如下：

(11)

式中：e1,e2,e0分别为误差信号，误差的微分及积分信号；β3,β4,β5为其相关增益。

2.3 模糊自抗扰转矩控制器设计

自抗扰控制器具有传统PI控制所不可比拟的优良控制性能，但是其参数过多，导致在实际应用过程中手工整定困难[13]。利用模糊控制不依赖于被控对象的精确数学模型并可在一定的参数变化范围内找到最合适的控制参数的特点，制定相应的模糊规则，根据{e1,e2}的输入在线调整自抗扰的参数，使其在不同的运行状态下自动逼近最佳的{β3,β4,β5}，大幅提高了系统的自适应能力。

在控制器设计中，模糊变量分别为输入量e1,e2，输出量为Δβ3,Δβ4,Δβ5。根据偏差大小选取其模糊论域，e1,e2分别为[-1,1]，[-10,10]；Δβ3,Δβ4,Δβ5分别为[-0.3,0.3]，[-0.3,0.3]，[-0.06,0.06]。隶属度函数采用控制分辨率较高的三角形函数并且左右对称，定义了7个模糊子集，表示成{PB(正大),PM(正中),ZO(零),NS(负小),NM(负中),NB(负大)}。模糊推理采用推理过程易于图形解释的Mamdani型，解模糊化为工业控制中广泛使用的平均加权法。根据专家经验建立的模糊规则表如表1所示。

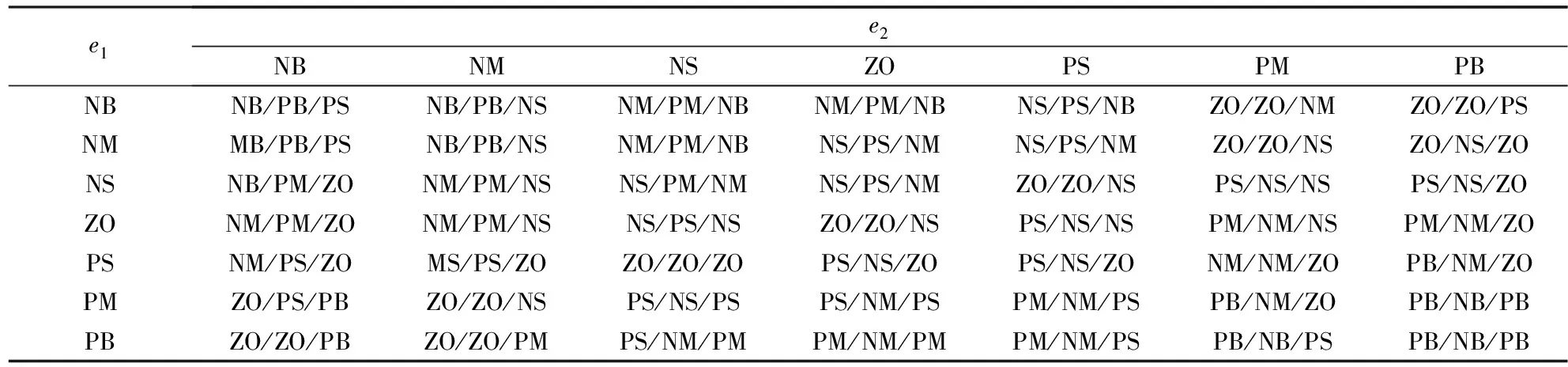
表1 Δβ3，Δβ4，Δβ5模糊规则表

由表1的模糊规则及模糊推理的解模糊化算法可以得到修正参数Δβ3，Δβ4，Δβ5代入式(12)中：

(12)

从而实现ADRC中参数在一定范围内的在线自整定，增强了系统的自适应能力。得到的自适应模糊自抗扰转矩控制器结构如图2所示。

图2 模糊自抗扰转矩控制器框图

3 PMSM模糊自抗扰转矩伺服系统

PMSM转矩控制伺服系统如图3所示，整个伺服系统采用矢量控制方法，控制策略采用直轴电流分量id=0。在id=0的条件下电机输出的电磁转矩与交轴电流iq成正比，此伺服系统转矩环控制为模糊自抗扰控制，通过TD安排过渡电流目标信号，在减少噪声干扰的同时，可快速无超调的达到目标值；ESO能实时观测系统的状态量及扰动；通过NLSEF对系统进行补偿，实现了目标信号“小误差大增益和大误差小增益”非线性控制，利用模糊控制实现对ADRC参数的在线自整定，提高了系统的自适应能力，有效减小了系统的稳态误差，并在较大范围达到最优控制。

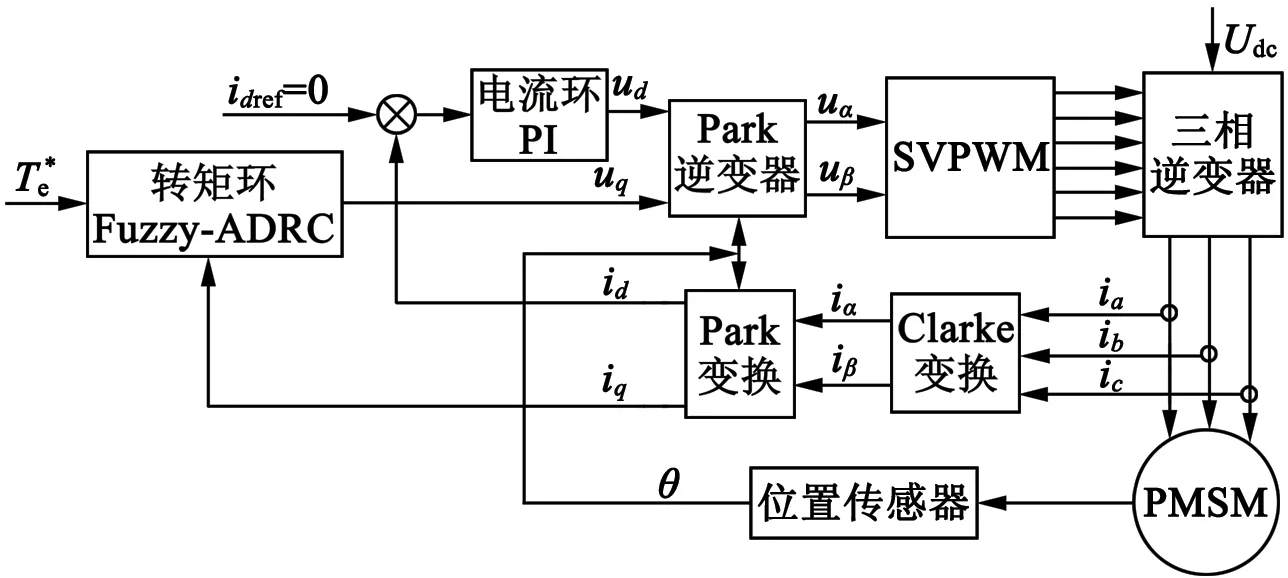
图3 模糊自抗扰转矩伺服控制系统

4 对比仿真与实验结果分析

4.1 对比仿真与结果分析

为验证PMSM转矩控制系统的性能，在MATLAB/Simulink中对基于模糊自抗扰的PMSM控制系统进行了仿真并通过实验进行了验证。为了验证模糊自抗扰具体的控制效果，本文将其与传统的PI控制进行对比。PI控制参数调节采用试凑法，过大的P值可以提高响应速度但是会造成超调甚至控制系统的振荡，I值的大小决定了系统的稳态精度，因此P值从小向大调节直到出现振荡，I值从大向小调节要保证静态精度，最终PI控制参数调整为P=0.5，I=0.02；在Fuzzy-ADRC系统中，调节参数较多，可根据韩京清提出的与斐波那契数列相关的整定方法[14]，最终参数的调节值为β1=800，β2=8 300；α1，α2分别为0.5和0.25；r，h0为10 000和0.002，仿真如下结果。

图4为模糊自抗扰控制与传统PI控制的目标电流iq响应时间对比，在t=0.1 s时给定目标值为6 A，Fuzzy-ADRC的电流响应时间大约0.015 s而PI的响应时间为0.05 s，相对于PI响应时间减少了约70%。

图5为二者的稳态电流的对比，相比于传统PI，Fuzzy-ADRC的稳态电流误差为1 mA，而PI的稳态电流误差大约为2 mA，有的已超过4 mA。这是由于Fuzzy-ADRC中ESO可以实时对内外扰动进行估计并补偿，因此相对于PI控制拥有更小的电流稳态误差。

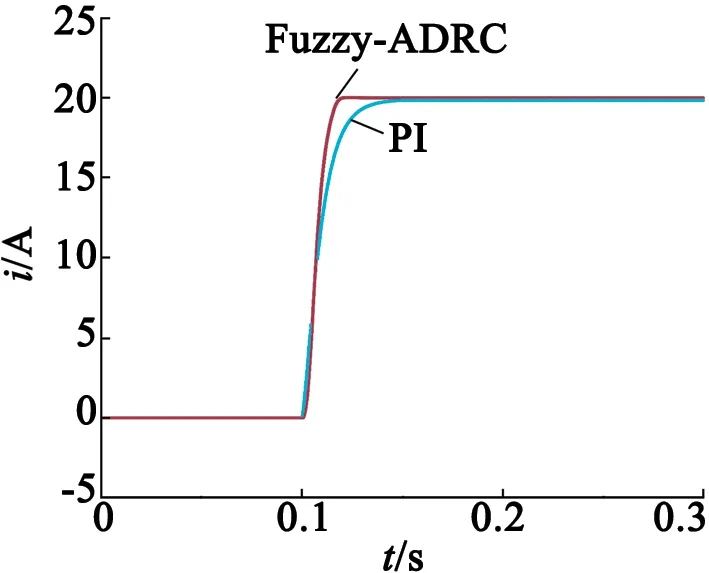
图4 交轴电流响应曲线仿真对比

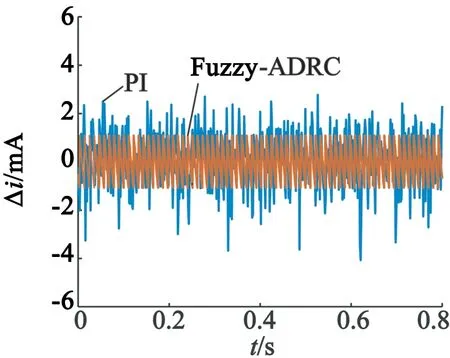
图5 交轴电流稳态误差仿真对比

图6为二者的转矩响应对比。由于电机为表贴式PMSM，采用id=0的控制方法，由式(4)可知，电磁转矩与交轴电流iq成正比关系，所以仿真的响应时间与图3保持一致。

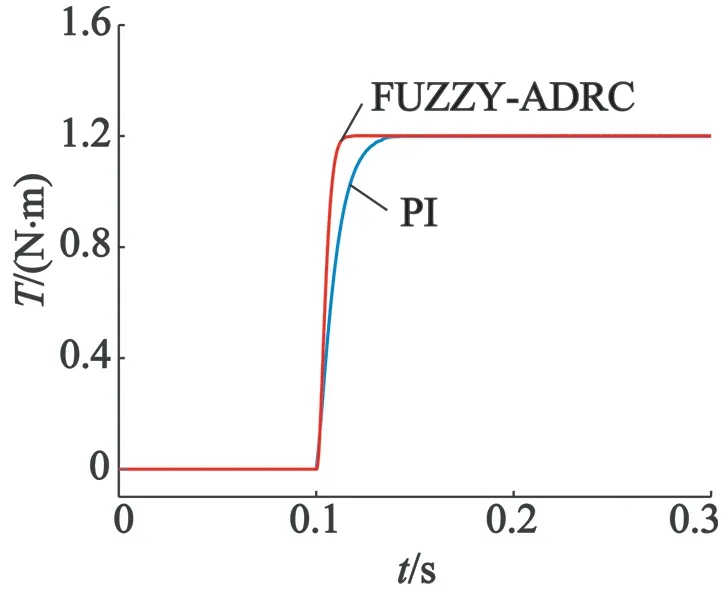
图6 电磁转矩响应曲线仿真对比

4.2 实验及结果验证

为了对仿真分析进一步验证，本文进行了实验验证，所使用的表贴式PMSM具体参数如表2所示。

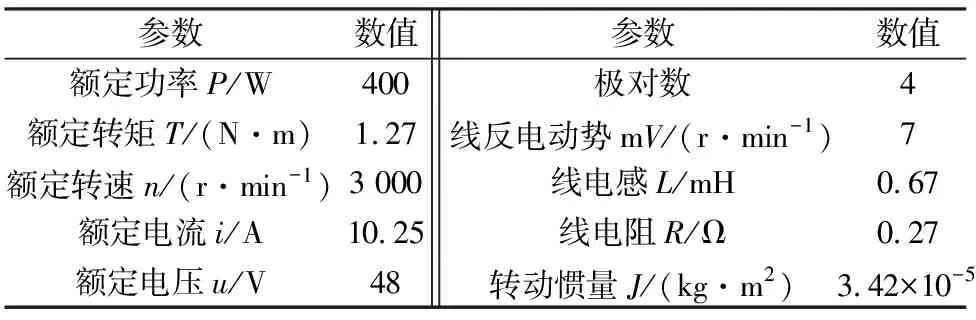
表2 永磁同步电机参数表

通过CAN总线采集的实验数据如图7、图8所示。

图7是实验中的电流响应曲线，图8是实验中的稳态误差对比。可以看出，实际控制时的结果与仿真结果基本一致，模糊自抗扰算法的响应时间基本在0.02s以内，传统的PI控制算法需要0.06s左右才响应，并且传统PI控制稳态误差相对于模糊自抗扰控制也更大。

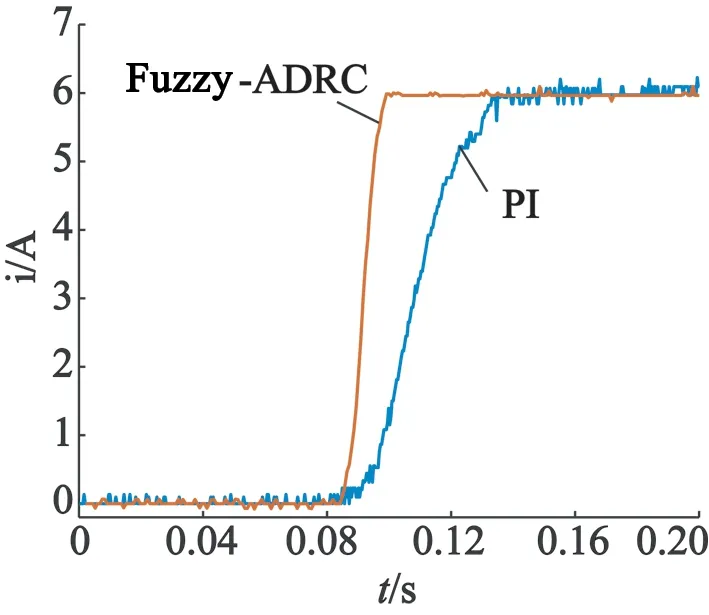
图7 交轴电流响应曲线实验对比

图8 交轴电流稳态误差实验对比

5 结 语

为满足对电动汽车转矩模式的控制需求，本文设计了PMSM转矩控制器并将模糊ADRC策略综合应用于电动汽车PMSM伺服系统转矩控制中，针对ADRC中的参数较多，手工整定困难问题，通过模糊控制使得NLSEF的反馈参数模糊化，实现了参数的自整定，提高了系统的自适应能力，达到了良好的控制效果。通过与传统PI控制算法的仿真及实验结果对比，在转矩响应时间方面减少了约70%的响应时间，有了明显提高，在稳态误差方面也有大约50%幅值的削减。

[1] 黄庆,黄守道,伍倩倩,等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报,2013,28(9):294-301.

[2] 戴彦.基于电动汽车的永磁同步电动机模糊自抗扰控制研究[J].微特电机,2015，43(7):85-88.

[3]KARABACAKM,ESKIKURTHI.Speedandcurrentregulationofapermanentmagnetsynchronousmotorvianonlinearandadaptivebacksteppingcontrol[J].Mathematical&ComputerModelling,2011,53(9-10):2015-2030.

[4] 王宝金.电动汽车永磁同步电机驱动及控制方法研究[D].哈尔滨：哈尔滨工业大学,2010.

[5] 续丹,雒焕强,房念兴,等. 永磁同步电机分数阶与滑模变结构复合控制研究[J].西安交通大学学报,2012,46(5):132-136.

[6]YUJ,CHENB,YUH,etal.Adaptivefuzzytrackingcontrolforthechaoticpermanentmagnetsynchronousmotordrivesystemviabackstepping[J].NonlinearAnalysisRealWorldApplications,2011,12(1):671-681.

[7] 贾洪平,孙丹,贺益康.基于滑模变结构的永磁同步电机直接转矩控制[J].中国电机工程学报,2006,26(20):134-138.

[8] 李婉婷,厉虹.永磁同步电机自抗扰控制技术研究[J].电气传动,2015,45(9):20-24.

[9]DONGQD,VUTT,HANHC,etal.Neuro-fuzzycontrolofinteriorpermanentmagnetsynchronousmotors[J].JournalofElectricalEngineering&Technology,2013,8(6):1439-1450.

[10]UDDINMN,ABIDOMA,RAHMANMA.Developmentandimplementationofahybridintelligentcontrollerforinteriorpermanent-magnetsynchronousmotordrives[J].IEEETransactionsonIndustryApplications,2004,40(1):68-76.

[11] 李崇坚.交流同步电机调速系统[M].北京:科学出版社,2013.

[12] 韩京清.自抗扰控制技术--估计补偿不确定因素的控制技术(精)[M].北京:国防工业出版社，2008.

[13] 薛薇,路鸦立.永磁同步电机调速系统的模糊自抗扰控制[J].电机与控制应用,2013,40(8):57-60.

[14] 韩京清.扩张状态观测器参数与菲波纳奇数列[J].控制工程,2008(s2):5-7.