无定子磁链观测的永磁同步电机直接转矩控制

郑云广,陆 可,谢建隆

(西南交通大学，成都 610031)

0 引 言

永磁同步电机(以下简称PMSM)具有体积小、效率高、功率密度大等特点，被广泛应用于工业和交流传动领域。PMSM直接转矩控制(以下简称DTC)结构简单，对电机参数依赖较小，鲁棒性强等特点受到广泛关注[1]。

传统PMSM DTC利用6个有效电压矢量，通过优选电压矢量的方式对定子磁链和转矩进行调节，利用磁链滞环和转矩滞环形成双闭环控制，以定子磁链的位置信号作为扇区判断标准选择开关表[2-3]。与矢量控制相比，电流解耦不彻底，磁链和转矩波动较大。为了克服DTC中转矩脉动较大等问题，有文献提出通过将电压矢量细分达到削弱转矩脉动的目的[4]；文献[5]通过分析滞环宽度对控制性能进行优化，获得了较低的电流谐波含量。文献[6]对不同策略下电流与磁链给定的关系进行研究，磁链计算不能避免，计算量较大。针对DTC中磁链波动较大的问题，文献[7]引入模糊逻辑控制器代替滞环比较器，有效抑制了转矩脉动，但仍需要对磁链进行实时计算。文献[8]和文献[9]基于有效电压矢量优化的思想，分别提出电压矢量评估因子和最小电压矢量偏差的策略。文献[10]提出了一种基于空间矢量调制的方法，但由于要对磁链差进行实时估算，计算较为复杂。传统的直接转矩控制往往建立在静止的α-β坐标系下，仅靠定子磁链和电磁转矩滞环控制，不能对三相电流进行彻底的解耦。因此当一个空间电压矢量改变定子磁链时，没有顾及对电流的影响。为了改善电流波形，往往通过磁链限幅或者其他磁链给定算法来实现[11]。

为了获得良好的电流特性，同时保持DTC结构简单，强鲁棒性的特点，在传统直接转矩的基础上，结合表贴式PMSM的特点，分析了PMSM电磁转矩和6个有效空间电压矢量之间的关系。在d-q坐标系的基础上，分析电磁转矩和电压矢量之间的关系，选择出能同时兼顾电流调节的优选电压矢量，在调节电磁转矩的同时达到电流的限制，保障电机稳定运行。

1 系统模型和传统DTC

1.1 三相S-PMSM数学模型

取永磁体磁链方向为d轴正方向，在d-q两相旋转坐标系下的PMSM电压方程：

(1)

三相表贴式PMSM转矩方程：

(2)

式中：ud，uq分别为d-q坐标系下的d,q轴定子电压；Rs为定子电阻；id，iq为d，q轴定子电流；ψd，ψq分别为d,q轴磁链;p为极对数。

PMSM运动方程：

(3)

式中:Te为电磁转矩；Tl电机负载转矩；J为电机转动惯量；ωr为电机转子机械角速度；RΩ为电机阻尼系数。

1.2 传统DTC方案

传统DTC系统采用磁链转矩双闭环，通过滞环比较器和查表的方式选择合适的电压矢量使电机磁链轨迹接近正六边形或标准圆。其控制方案原理如图1所示。

图1 传统DTC控制框图

PMSM传统DTC控制方案是基于α-β静止坐标系下由感应电机控制策略推广而来。通过检测电机定子电压电流，计算出电机的定子磁链幅值、角度和转矩。将计算值分别与给定值进行滞环比较，根据磁链位置和转矩控制信号选择合适的电压矢量。转速误差经过PI调节器后得到转矩给定，而磁链的给定则由不同的控制目标分别采取不同的控制算法。如最大转矩电流比控制、恒定子磁链控制等。估计后的磁链要进行扇区判断，就需要得到磁链角度。磁链幅值和磁链角度可由下式求得：

(4)

(5)

可以看出，以磁链为控制目标的控制方式由于磁链的积分和反三角函数计算，导致计算量较大，并且由于积分运算，容易受采样误差影响。

2 无磁链观测DTC方案

2.1 转矩控制原理

PMSM运行矢量如图2所示。

图2中，ψf,ψs分别为永磁体磁链和定子磁链;is为定子电流;δ为定子磁链与d轴夹角;θ为d轴与a相轴线夹角。

由于表贴式PMSM交直轴气隙相差很小，因此，可令Ld=Lq。结合式(2)，PMSM电磁转矩可以表示：

(6)

式中：ψq为电机q轴磁链。

此时，从式(6)可以看出，除了负载角δ，还存在变量ψs。在一定范围内，负载转矩随着磁链幅值和负载角正弦值的增加而增加。用一个电压矢量同时实现两个变量的最优控制，计算比较复杂。对于PMSM，定子磁链ψf由永磁体直接产生，是一个恒定值。因此，对电机转矩进行关于ψq的微分运算，得到下式：

(7)

当忽略定子电阻压降时，有：

(8)

因此，可以通过控制q轴电压分量变化最大达到PMSM电磁转矩变化最快的目的。这就意味着若使逆变器选择q轴分量较大的电压矢量作用于电机，达到电磁转矩快速变化的目的。此时，转矩环可通过对交轴电压uq的直接控制实现，对转矩的控制也从定子磁链的转矩角转移到电压矢量的交轴分量上来。

但以此作为开关表确定依据，有可能造成定子磁链幅值过大，使定子绕组磁链饱和，最终电机无法稳定运行，因此需要对磁链进行控制。

2.2 电流限制

结合矢量控制理论，表贴式PMSMid=0控制算法简单，易于实现，能同时实现最大转矩电流比控制，被广为采用[12]。传统DTC的id=0控制策略利用直轴电流id与磁链幅值的一一对应的特点，在一个控制周期内，转矩已知，利用式(9)计算出磁链幅值的给定，进而到id=0的控制效果。借鉴这个思路，如果对直轴电流id进行控制，那么在某个已知转矩下，就一定有与之对应的定子磁链幅值，因此就不需要对磁链幅值进行限制。其次，由于定子磁链是一个矢量，如果以电流环替换磁链环，将导致磁链角或者负载角δ的缺失。基于PMSM的位置传感器特点，采用定子磁链角度θ经过计算代替负载角δ。

(9)

由式(1)中电压模型可知，id与直轴电压ud密切相关。忽略定子电阻，电机稳态运行时有：

(10)

因此，通过ud可以达到快速控制电流id的目的，并且，电流变化会随着直流母线电压的增加而增大。因此，母线电压要合理选择，过高则脉动较大，控制周期变小;过低则电机运行不稳定，控制响应变慢。

图3为三相两电平逆变器电压矢量图。图3中θ为转子与定子绕组A相轴线的夹角，d轴正方向为永磁体磁链方向。图4为空间电压矢量随转子位置变化规律。以转子磁链位置为参考，将空间电压矢量等分为6个扇区，以ud，uq为控制目标，以转矩响应为优先选择对象，重新选择开关表。

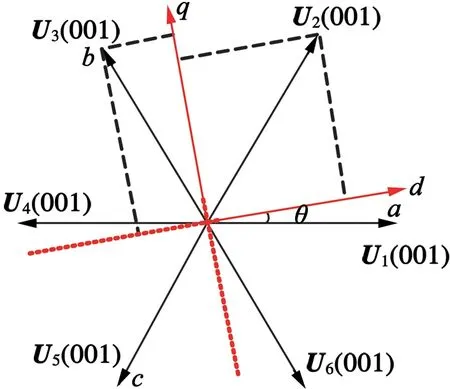
图3 电压矢量图

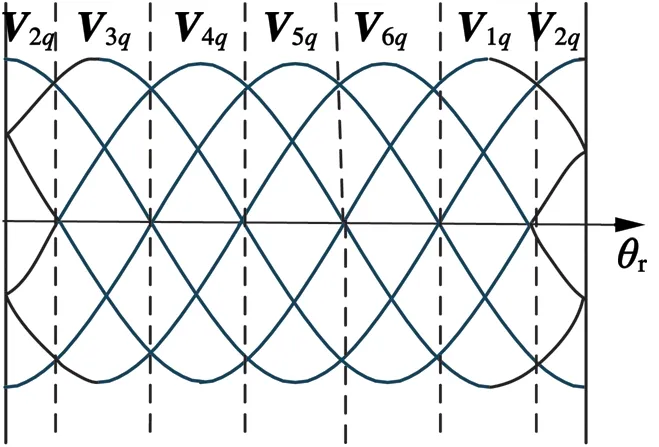
图4 空间电压矢量随转子磁链位置θr变化规律

图5为定子电流与电压矢量关系图。图5中，ΔTs为电压矢量作用时间，is(n)为电压矢量作用后下一个时刻定子电流状态。

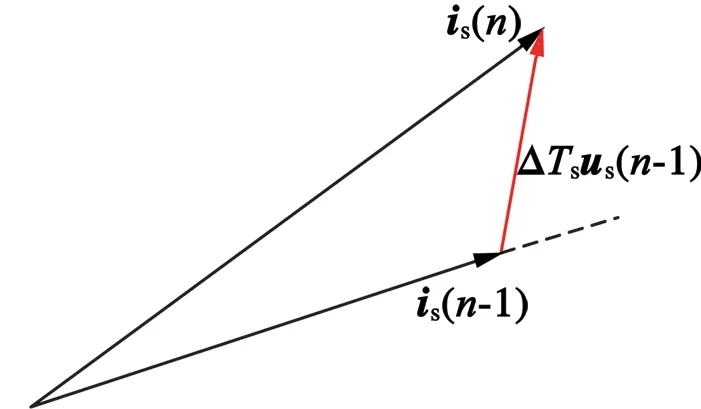
图5 定子电流和电压矢量关系图

基于无磁链观测的PMSM DTC控制框图如图6所示。转矩给定由转速差经过速度调节器得到，将转矩给定T*与实际转矩进行滞环比较输出转矩控制信号。将原本的磁链控制环由d-q坐标下的电流环来代替，新的优选矢量开关表代替传统开关表，输出的开关信号由转矩控制信号τ，电流控制信号以及位置传感器的位置信号得到。

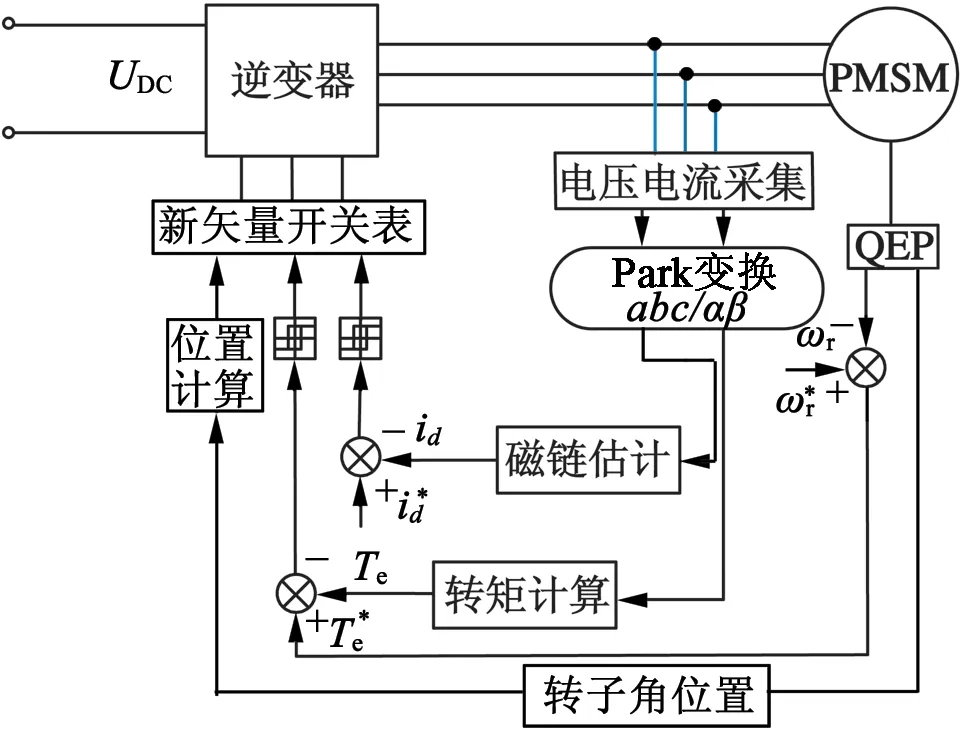
图6 基于无磁链观测的DTC控制框图

3 仿真验证

为验证控制方案的正确性和有效性，进行了仿真分析。以一台额定功率为150 kW的表贴式PMSM为研究对象，具体参数：额定转速为23.8 r/min，定子电阻为0.8 Ω，d,q轴电感为23 mH，电机极对数为30对极，永磁体磁链为7.144 Wb。仿真时给定转矩为50 000 N·m，转速为10 r/min，t=0.5 s时转速突变为23.8 r/min。

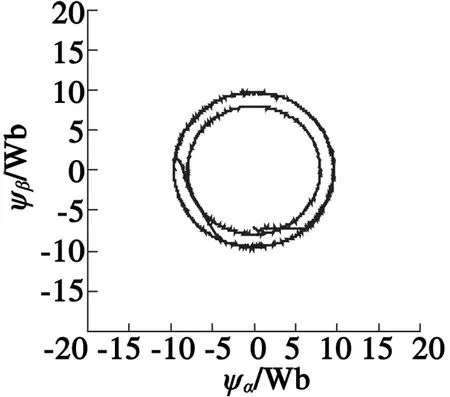
(a) 定子磁链轨迹

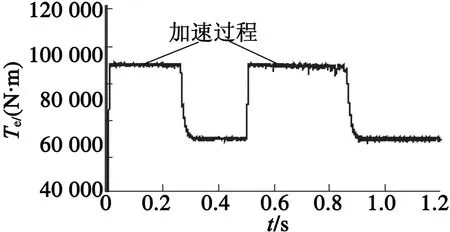
(b) 电磁转矩

图7定子磁链和转矩仿真波形

图7分别为定子磁链轨迹和电磁转矩波形。可以看出，磁链幅值得到了很好的控制，轨迹为圆形，其中，磁链幅值变大的过程为转矩增大的过程，到达转矩限幅后，磁链幅值维持在可控范围之内。虽然采用有差的滞环控制，但磁链轨迹相对平滑，说明上述方案能实现对定子磁链的控制。从图7(b)的电磁转矩波形看出，转矩有较快响应，因为选择矢量依据转矩响应优先的原则选取。稳态转矩脉动在4%左右，比传统DTC有所下降。其次，由于是电机转矩直接响应电压矢量的变化，因此，输出电磁转矩对给定转矩的相应较快，其中直流侧母线电压的大小会影响转矩波动情况，并且在大转矩下转矩脉动效果抑制更明显。

电机转矩阶跃响应如图8所示。可以看出，在负载转矩突变时，电机能快速跟踪负载转矩变化做出调节，并且没有过大的超调，达到了理想的控制效果。

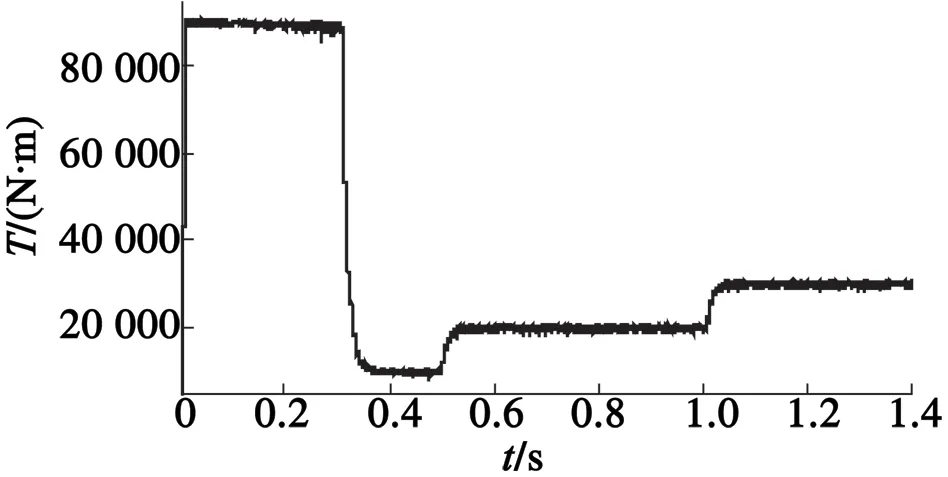
图8 电磁转矩阶跃响应波形

图9为三相PMSM定子电流。可以看出，在0.3s和0.9 s分别达到稳态。在0.5 s时转速突变时，能较快响应指令。并且定子电流脉动较小，正弦畸变较小，达到匀速后电流下降相对平滑。说明所选的电压矢量在不进行磁链估计和限幅的情况下，仍能对电流进行控制，同时达到间接的磁链控制效果。

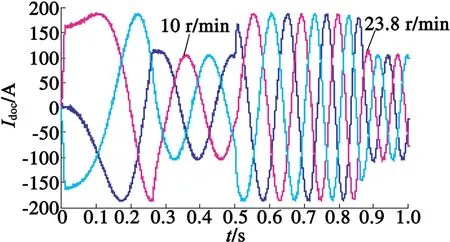
图9 三相定子电流仿真波形

4 结 语

针对传统的DTC磁链估计计算复杂，计算量较大，电流控制效果不理想等问题，提出了基于定子磁链角为基准划分扇区，增加直轴电流id控制环的控制方案。在电压矢量的选择中，将电压矢量分解到旋转坐标d,q分量，并基于转矩响应最优的原则选取电压矢量。该方案不需要对磁链的实时计算，同时达到了转矩的快速响应和定子电流畸变小的控制特性。最后，通过仿真验证了该方案的正确性和有效性。

[1] 杨影,陈鑫,涂小卫,等.占空比调制的永磁同步电机直接转矩控制[J].电机与控制学报,2014,18(4):66-71.

[2] 李耀华,马建,刘晶郁,等.电动汽车用永磁同步电机直接转矩控制电压矢量选择策略[J].电机与控制学报,2012,16(4):43-49.

[3] TAKAHASHI I,NOGUCHI T.A new quick-response and high-efficiency control strategy of an induction motor[J].IEEE Transactions on Industry Applications,1986,22(5):820-7.

[4] 陈振,刘向东,廖晓钟,等.基于十二扇区细分的永磁同步电动机直接转矩控制[J].微特电机,2011,39(5):42-6.

[5] MATHAPATI S,BOCKER J.Analytical and offline approach to select optimal hysteresis bands of DTC for PMSM[J].IEEE Transactions on Industry Electronics,2013,60(3):885-95.

[6] 曹林柏,赵宏革,张智远,等.一种永磁同步电动机直接转矩控制策略研究[J].微特电机,2016,44(4):47-51.

[7] 李光叶,万健如,刘英培,等.基于模糊零矢量永磁同步电机直接转矩控制[J].电力自动化设备,2009,29(9):31-5.

[8] XIA C,WANG S,GU X,et al.Direct torque control for VSI-PMSM using vector evaluation factor table[J].IEEE Transactions on Industry Electronics,2016,63(7):4571-83.

[9] 陈炜,艾士超,谷鑫.基于最小电压矢量偏差的永磁同步电机直接转矩控制[J].电工技术学报,2015,30(14):116-21.

[10] 王斌,王跃,王兆安.空间矢量调制的永磁同步电机直接转矩控制[J].电机与控制学报，2010,14(6):45-50.

[11] FAIZ J,MOHSENI-ZONOOZI S H.A novel technique for estimation and control of stator flux of a salient-pole PMSM in DTC method based on MTPF[J].IEEE Transactions on Industry Electronics,2003,50(2):262-71.

[12] 李耀华,刘卫国.永磁同步电动机直接转矩控制系统的最大转矩电流比控制[J].微特电机，2007,35(1):23-6.