例谈引入 演绎精彩

赵玉兰

摘 要：职业学校的学生基础薄弱，思维能力差，加之数学本身与其他学科相比又相对抽象，枯燥，从而使得学生学起来困难，甚至与出现抗拒性。教师应根据教材的特点，结合学生的学习现状，巧妙设计引入方法，吸引学生的兴趣，将学生的注意力吸引到课堂中间来，让学生学会学习数学，激发他们学习的动力，拓展思维。

关键词：职业学校 引入 方法

中图分类号：G718 文献标识码：C 文章编号：1672-1578（2017）05-0280-01

德国教育家第斯多惠说过：“教学的艺术不在于传授的本领，而在于激励、唤醒、鼓舞。”在一线数学课堂教学过程中，引入是教学的第一步，在引入环节设计的恰当与否，将关乎到对概念的正确理解，更是激发学生思维，鼓舞学生求知若渴的动力。本文就数学课堂的引入设计，例谈一些方法。

1 通过类比归纳引入新知

创造性思维是数学思维中一个重要的组成部分，而通过“类比”的思维训练是让学生发展其创造性思维的一种重要的手段。通过类比，让学生自主动脑思考，研究，达到学生掌握了知识，锻炼了思维，学会了方法的目的。

例如，在直线与抛物线的位置关系的教学过程中，首先给出这样的一个问题：过点P（0，1）的直线l，斜率为k，当k为何值时，直线l与双曲线x2-y2=1相交，相切，相离？

学生解题，解题之后教师进行讲解，并由此回顾直线与双曲线的三种位置关系：相交：一个或两个交点；相切：一个交点；相离：没有交点。随后结合上述方法，给出例题，让学生解答。

例1.已知抛物线的方程为y2=4x，直线l过定点P（-2，1）斜率为k，当k为何值时，直线l与抛物线y2=4x只有一个公共点？有两个公共点？没有公共点？

在此过程中，学生不仅学会了类比的思想方法，更将直线与圆锥曲线位置关系这一系列的问题能够更加系统，透彻，深入的理解了。

2 创设问题情境引入新知

美国心理学家布鲁纳指出：“教学过程是一种提出问题，解决问题的持续不断的活动”。数学知识并非无端产生，将数学概念，定理等的教学置身于具体的情境中，是由其本身所决定的。故问题情境在课堂中的地位首先是在概念讲解时设计问題情境引入，那么如何设计才能符合学生的认知程度，将学生的“心”抓住呢？

2.1联系生活实际创设问题情境

数学来源于生活，是对生活的抽象化与形式化，而抽象化与形式化的特点又使数学成为具有广泛应用的工具学科和技术学科。现代数学已渗透到生活的各个领域，据此，我们设计情境引入时，要尽可能将数学“还原”到生活当中，让学生从生活情境中体验数学、提炼数学、“发现”数学、理解和认识数学，这样学生就不会感到数学的抽象，难以理解。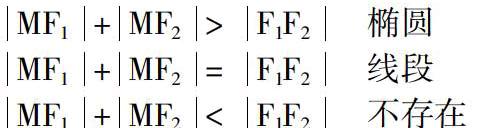

例如，在函数的单调性教学中，首先给出一张北京市今年8月8日一天24小时内气温随时间变化的曲线图。

引导学生识图，捕捉信息，启发学生思考：（1）当天的最高温度、最低温度以及何时达到？（2）哪些时段温度升高？哪些时段温度降低？

归纳：用函数观点看，其实就是随着自变量的变化，函数值是变大还是变小。

这样，由生活情境引入新课，由观察生活中的数据，图像，来引申为数学问题，拉近与学生的距离，激发了学生的兴趣。

2.2 联系旧知创设问题情境

数学知识之间是相互关联的，有些新的知识都是建立在已有知识层面上，是对旧知识的进一步认知，拓展，延伸，由旧知引导学生自主归纳小结得到新知，使得学生对于知识的形成过程更加的清楚明了，对于整个知识体系，框架结构也更加清晰。

例如，在直线与圆的位置关系中，可这样引入：观察日出的景象，在动画中，可以抽象出哪些几何图形？结合初中内容，请学生回顾直线与圆有哪几种位置关系？在平面几何中，你将用怎样的方法判断是哪一种位置关系呢？试说说。

定义法：看直线与圆公共点的个数。

比较法：圆心到直线的距离d与圆的半径r作比较。

在平面直角坐标系中，如何根据直线与圆的方程判断它们之间的位置关系？引例、判断直线3x-4y+5=0与圆x2+y2=2的位置关系。

师生共同分析，探究，学生思考，回答。通过给出具体的直线与圆的方程，分析判断位置关系的方法。将问题直接抛给学生，让学生结合已经学习的内容想方设法来解决，在解决问题中获得数学知识，解题方法等，让学生体验到数学的“简单”。

3 设计动手实验引入新知

数学知识并非无端产生，而是先人在无数的经验，实验中总结得到的。“纸上得来终觉浅，绝知此事要躬行”，通过设计一些动手的实验操作，在带给学生新鲜的课堂氛围的同时， 也让学生亲身经历数学知识概念的产生发展过程；让抽象的数学化为简单的，直观的；让学生在实验中观察，思考，总结。

例如，在椭圆的教学过程中，可以设计这样的一个活动：

（1）取一条定长的细绳，把它的两端都固定在黑板的两个不同的点F1、F2处，套上铅笔，拉紧绳子，移动笔尖，画出的轨迹是什么曲线？（在这一过程中，你能说出移动的笔尖（动点）满足的条件吗？）（2）改变两定点之间的距离，使其与绳长相等，画出的图形还是椭圆吗？（3）当绳长小于两图钉之间的距离，还能画出图形吗？通过作图，让学生体会椭圆形成的过程，并引导学生总结概括：

MF1+MF2> F1F2 椭圆

MF1+MF2= F1F2 线段

MF1+MF2< F1F2 不存在

椭圆定义：平面内与两个定点F1、F2的距离的之和等于常数（大于F1、F2）的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。（强调两点：①平面内 ②F1F2<常数）

总之，课堂的引入方法有很多，教学有法但无定法，在教学中，依据教师自身的教学风格和学生的情况，进行灵活转变，应用，不断探索更好，更合适的引入方法，以美好的开端开始每一节课，带领学生走进广阔的数学领域，更好的激发学生的潜能，鼓舞学生不断前进！

参考文献：

[1郑子瑜，将问题情境引入职高数学课堂[J].中等职业教育，2009（35）：46-48.

[2]钱丹丹，例谈职高数学课堂上的引入方法[J].宁波职业技术学院学报，20011年6月.

[3]吴素波，情境创设在职高数学教学中的操作策略[J].数理化学习，2012年第4期.

[4]邹青，谈谈如何在职高数学教学中引入生活化[J].中国科教创新导刊，2013年第20期.