浅谈中小学数学思维训练与培养

向乾华

摘 要：知识经济对人才的培养提出更新、更高的要求。而探索精神萎缩，思维能力低下，创新意识单薄，极大妨害了学生整体素质的提高。本文从数学思维概述出发，给出了思维的内涵、特点，旨在从中找出适应中国国情的数学思维训练的出发点。系统阐述了思维的训练与培养，旨在结合实例，找出中小学数学思维的一条有针对性和可行性的培养之路。给出了研究成果的落实建议，以便对日后更好地进行思维训练提供较好的基础，同时期待对中小学教师与学生有真正意义上的帮助。

关键词：数学思维 训练 培养 研究

中图分类号：G633.6 文献标识码：C 文章编号：1672-1578（2017）05-0100-01

全国第三次教育会议指明：学生应见证知识的产生和发展，教师应培育学生的探索精神和创新方面的思维。

我们开展“思维训练与探究”的目的，旨在：改变教与学的方式，调动学生思维的活跃性和创造性，真正实现“促进每一个学生的发展”；更新教师的教育观念，提高将先进理论运用于新课程实践操作的水平，培养具备创新精神与能力的教师。

1 数学思维概述

目前，数学思维研究是我国数学家乃至世界数学界都关注的一个活跃的研究方向。

1.1 数学思维的涵义

数学思维即数学地思考与解决问题的思维活动形式。如果把数学思维当做是人的心智的一种内部活动，那么数学知识就是这种内心活动的的外观表示。数学意识和数学思想方法等都是数学思维活动的菁华，也可以说成是数学思维的宏观归纳。

1.2 数学思维的特点

对于数学思维的特点，其一，指的是数学本身的 “逻辑的严密” 与“高度抽象性” 与“结论精确性”与“广泛的应用”；其二，正如徐利治教授指出的：类似于自然科学，数学思维有观察、实验、类比、归纳等特征。

2 数学思维的训练

数学思维的训练主要是对学生进行数学思维活动的训练。

例如，树上有8只小鸟，又飞来4只，这是数学素材；根据这些素材形成数学构思就是数学思维。例如，树上有8只小鸟，又飞来4只，飞来的比原来的少几只？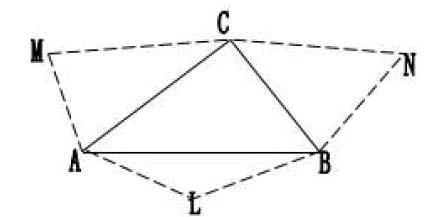

需要指出的是：培养学生的思维逻辑能力要按部就班地落实在数学教学的各个层面。

2.1 激发思维动机

最佳的教学动机是学生对知识萌生内在的兴趣。比如，教学“按比例分配”，应先让学生明白学习按比例分配的目的：只有平均分配不合适或不合理，才出现这种新的分配。教学时可以这样设计：把搬10000个部件的任务交给李师傅和王师傅，完成后要把1000元劳动费分给他们，结果李师傅完成了6000个和王师傅完成了4000个。这时将钱均分公平吗？可见，创建思维情景，是对其进行思维训练的重要方式。

2.2 理清思维脉络

学生思维能力的发展紧跟着知识发展。教学的关键就是使学生的思维脉络变得清晰。著名数学家波利亚可以将学习分为三个阶段：一为探索阶段，二为阐明阶段，三为吸收阶段。下面遵照三原则来分析一道题：

已知六条棱，求作四面体。

（1）首先，让学生观察一下用“机械制图的方法”解决实际问题的情形；（2）引导学生讨论：用直尺和圆规精确的解决这一问题时，四面体的哪些元素必须在图上作出来，试着把它们也作出来，其中AM=AL，BL=BN，CM=CN；（3）将此图复制在硬纸板上，糊成一个立体模型。

学生思维可能“卡壳”，教学时可通过“迁移”、“转化”对学生加以疏导，使学生思维更加清晰。

3 数学思维的培养

解决问题经常需把未知的问题转化成已知的问题。应根据具体情况合适地运用分析与综合、具体与抽象、求同与求异、一般与特殊等思维形式。

3.1 分析与综合

思维主要是通过分析、综合来进行开展的。如：一工厂要生产一批零件，计划每天生产30个，50天完成。实际每天生产50个，按这种速度，会提前几天完成？此题就应该用到分析的方法。

恰当地利用分析或综合，条件与问题会越来越近，从而形起清晰的思维脉络。

3.2 具体与抽象

具体与抽象在人的认识中互相联系和转化。如：在学习“圆柱体展开图”时，教师通过实物模型，并让学生自己剪开后，观察展开后对应关系，很快地归纳出侧面积的等公式。这样一来，学生不仅记住了而且理解了圆柱体侧的面积公式，同时也增强了学生的操作意识与能力，进一步培养了学生把抽象化为具体的思维方法。

3.3 求同与求异

求同与求异就是找出共同点或找出不同点。如：多项式的各项有公因式，可以把这个公因式提到括号外面，将多项式写成因式乘积的形式，这种分解因式的方法叫做提公因式法。提公因式法就是求同的方法。

通过求同与求异的思维方法，不仅使学生知识体系得以完整建构，对学生多极化的思维方式也很有帮助，避免思维定势。

3.4 一般与特殊

学习往往遵循这条认识规律：特殊——一般——特殊。儿童学数时：两个苹果，三支钢笔……非常特殊且具体，他们是容易接受的。到了初中，学习了“代数式”。这里面，从数量到数，又从数到文字，再从文字到代数式，就是一个从特殊到一般再到特殊的认识过程。

4 结语

中小学数学教学，有目的、有步骤地对学生实施思维训练，不但对数学教学质量提高很有好处，对学生思维能力发展也大有作用。笔者认为，重要的是将目前的研究成果落到实处。马克思说过：“学习—实践—再学习—再实践”。只要有益于人才培养的思维规则就应该好好的去贯彻，让教师和学生真正掌握。

参考文献：

[1] （日）米山国藏著.数学的精神、思想与方法[M].毛正中等译.成都：四川出版社，1986.

[2] 王仲春等编著.数学思维与数学思想方法[M].北京：高等教育出版社，1989.

[3] 嚴士健主编.面向21世纪的中国数学教育[M].南京：江苏教育出版社，1994.4

[4] （美）G.波利亚著.怎样解题[M].阎育苏译.北京：科学出版社，1982.

[5] （美）D.A.格劳斯主编.数学教与学研究手册[M].陈昌平等译.上海：上海教育出版社，1999.

[6] 马忠林主编.数学思维理论[M].任樟辉著.南宁：广西教育出版社，2003.