基于脉动阵列的HEVC8×8整数DCT变换的设计与实现*
潘苏文,叶宇煌,郑明魁,陈志峰,杨秀芝
(福州大学 物理与信息工程学院,福建 福州 350116)
基于脉动阵列的HEVC8×8整数DCT变换的设计与实现*
潘苏文,叶宇煌,郑明魁,陈志峰,杨秀芝
(福州大学 物理与信息工程学院,福建 福州 350116)
文章基于脉动阵列实现HEVC(High Efficiency Video Coding)中8×8的整数DCT(Discrete Cosine Transform)变换,改进通常使用的蝶型算法。整体架构基于脉动阵列的思想,并采用中间值数据重组的设计,使得变换模块可同时实现行列变换操作。只需得到列变换的第一个值便可开始行变换,充分利用了PE单元,减少变换时间并提高计算模块的并行性。文中方法不仅适用于DCT变换,也可用于其他的8×8矩阵相乘,具有通用性。综合结果表明,该设计最高可工作在203.8 MHz的频率上,与其他算法相比时间上只需35个周期,且资源消耗较少。文中方法非常适合于HEVC视频编码对实时性的要求,为HEVC编码标准的硬件实现提供了参考。
高效率视频编码;离散余弦变换;FPGA;脉动阵列
0 引言
离散余弦变换最早是由Ahmed在 1974年提出[1],它具有很好的能量集中特性即所谓的去相关性,在图像处理和视频压缩领域占有重要地位。在先前的视频编码标准中,如MPEG-4、H.264/AVC都使用了DCT变换,并且对变换矩阵做了一定的改进,使其具有一定的规律性,有更好的快速变换算法,更适合编码压缩。一般对于图像的处理都不是基于一整帧,而是首先将一帧图像分解成多个变换块(Transform Units,TU),再对每块TU做DCT变换。目前新兴的高效率视频编码标准HEVC也采用了这种方法,HEVC的TU有4×4到32×32大小块,除了4×4大小的TU采用离散正弦变换(Discrete Sine Transform)外,其余的TU大小块都采用整数DCT变换[2]。HEVC灵活的TU划分提高了压缩效率,编码效率可以提高一倍,但同时也增加了复杂度。实现DCT需要多次进行乘法和加法的操作,带来了时间延时和面积消耗。
为了让DCT有更好的实现算法,前人做了很多的努力来减轻DCT/IDCT(Inverse Discrete Cosine Transform)所带来的密集的操作。Budagavi[3]等人利用DCT系数的奇偶可分解性和硬件共享技术来节约硬件开销,并提出了一个统一的架构实现正反DCT变换,由此大大减少硬件面积。Meher[4]等人避免使用常规乘法而是使用更少乘法器的多常数乘法(Multiple Constant Multiplication,MCM)算法。Ahmed[5]等人将DCT矩阵分解成更小的子矩阵来减少乘法次数,它的提升方案中更是可以完全将乘法去除。文献[6]将蝶型算法分别采用直接乘法器的M模式和使用加法和移位代替乘法操作的AS模式实现DCT变换。文献[7]将二维DCT变换转换成两个一维变换分别实现。
在这些方法中几乎都利用了DCT系数的对称性和反对称性属性以及蝶型思路去完成DCT变换。然而一旦利用了蝶型,那么整个算法的并行性就会有所下降。另外为了增加主频,还引入了多级流水处理,这会进一步消耗面积。本文不再基于蝶型算法,而是采用脉动阵列设计了DCT的硬件实现,试验结果显示,所设计的结构只有两级流水,具有相对较低的面积消耗和更高的工作频率。
1 DCT变换和脉动阵列原理分析
1.1 DCT原理分析
假设输入为M点的向量n=[n0n1…nM-1],对于一维DCT是一个线性变换,输出N=[N0N1…NM-1]的值可由式(1)得到[8]:
(1)
这里式(1)也可以写成矩阵运算形式
N=Cn
(2)
其中C为M点DCT变换矩阵,且C中对应索引(m,n)的系数值cmn为:
(3)
作为正交变换,反变换n=CTN。因为DCT有内核可分解的性质,因此可以把2D DCT分解成两个一维DCT进行运算。设X是一个N×N维的矩阵,则对X进行2D DCT有式(4):
Y=CXCT
(4)
从式(4)可以看出,其实二维DCT变换可以分解成串联的两次一维DCT变换,即
Y=ZCT
(5)
Z=CX
(6)
式中,Z为中间值矩阵。因此,在做二维DCT变换时可以运用一维DCT变换来计算,流程框图如图1所示。

图1 2D-DCT算法结构
1.2 脉动原理分析
脉动阵列是由卡内基-梅隆大学的KUNG H.T.教授最早提出。它是由多个处理单元(PE)按照一定互联规则组成的网络,有一维线性、二维矩阵阵列等。每个PE单元具有相同的功能,并且PE单元只能与自己相邻的PE进行通信,它们的通信是非常规则的,每个PE都有自己的内部存储器,用于寄存由邻近PE传过来的待处理的数据。
DCT变换当以矩阵相乘的形式表示时,可以理解为3个矩阵的相乘。矩阵相乘之所以可以用脉动阵列去实现,原因在于脉动阵列适合那些高度规则的算法实现,而矩阵相乘本身就是一个高度规则的算法形式。可以用DG依赖图去判断一个算法的规则性。所谓DG依赖图判断规则是指如果依赖图的任一节点沿某个方向的边都存在,则称DG是规则的,换句话说DG的所有节点具有相同形式的边。由于DCT变换算法最后可以用矩阵相乘的形式表示出来,用DG依赖图的判断规则可以判断得到矩阵相乘是一个高度规则的算法,因此矩阵相乘形式的DCT变换非常适合用脉动阵列的思想去实现,满足脉动设计的前提条件。
2 脉动阵列8×8 DCT的设计与实现
本设计基于脉动阵列高并行流水数据控制的特点,实例化多个PE单元同时进行DCT变换。传统PE阵列实现DCT变换要等到列变换做完后,继续再做行变换,这样使得PE单元过多地被闲置,为了避免在做列变换时PE的闲置,本文在得到列变换结果时即将其输出到输入数据处理单元,在数据处理单元中对中间值做数据重排,经过重排后的数据会被再次送入PE阵列中,这里从输出中间值到再次输入到PE单元中做下一次的行变换,中间只需两个周期的时间延迟。另外当得到二维DCT第一个结果时,下一个二维DCT变换也将开始,这样充分提高了PE单元的利用效率,减少了变换周期数。
2.1 整体架构
如图2所示,脉动阵列DCT的整体构架由输入数据处理单元、PE阵列(核心单元)、控制单元和结果转换单元4部分组成。输入数据处理单元对8×8大小块的TU残差数据和8x8 DCT系数的数据进行重排和延迟,将处理好的数据传给下个单元做处理。PE阵列单元由64个独立PE单元组成,每个独立的PE单元完成相乘和累加的操作。控制单元负责每个模块的协同合作和控制数据的输入输出。结果转换单元提取经过PE阵列处理后的最终DCT结果输出。
2.2 输入数据处理单元
如果一幅图像的位深为B,从帧内/帧间预测得到的残差值范围则为-2B+1到2B-1,这同时也将作为TU的数据。在HEVC中DCT的系数是由有符号的整数组成,这些系数值是通过缩放因子为2(6+E/2)放大所得到的矩阵,这里E=log2M,M为TU的大小。以上所提到的残差值和DCT系数以及经过列变换的中间值将作为数据处理单元的输入。
数据处理单元主要有两个功能:输入延迟和数据重PE阵列,第一象限是残差值的输入顺序,第三象限是DCT系数的输排。输入延迟如图3所示,坐标的第四象限是入顺序,横纵坐标轴所示为周期次序。第1周期X11(残差矩阵左上角的第一个值,以此类推X12,X18,X81...)和C11(系数矩阵左上角的第一个值,以此类推C12,C18,C81...)被送入P11单元;第2周期X21,C12被送入P11单元,X12、C11被送入P12单元,X11、C21被送入P21单元;到第8周期时,X18、C18送入P11单元,这样P11单元第一次列变换的8个数据全部输入完成,而P88在第8个周期则刚好接受X18、C81的最初两个数据,必须再经过8个周期才能将数据输入完成。
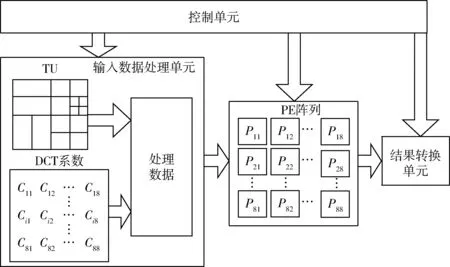
图2 系统整体框架
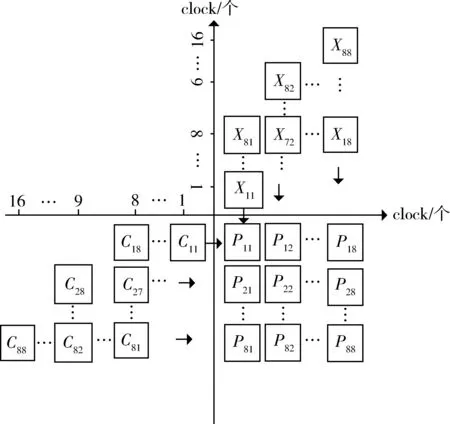
图3 数据输入顺序
在完成列变换之后每个PE单元都会存储一个结果值(中间值),这些值将会作为下一个行变换的输入值,因此需要将重新组织再输入。本文设计中在第9个周期将会在P11单元中得到第一个值Z11,在第10个周期会在P12、P21得到Z12、Z21,以此类推在第16个周期会得到列变换的最后一个值Z88。这些值一旦在PE生成就会被输出到一个寄存器组中,图4说明了中间值的输出顺序。被存储在寄存器组中的中间值会在下个阶段做行变换时与系数一起作为输入进入数据处理单元,重复列变换的操作。
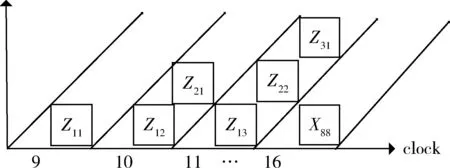
图4 中间值的输出顺序
2.3 PE阵列
PE阵列模块由64个独立的PE单元构成,每个PE的功能主要有:负责接收输入数据、结果输出、乘
法/累加操作、相邻PE之间数据通信等。在PE内部使用两个乘法器和两个加法器完成乘法累加核心功能,两个选择器控制数据的输入和结果的输出,如图5所示。图中所示PE内部电路图上下对称,上半部分主要完成列变化,下半部分负责行变换,上下两部分功能完全相同,不同的地方在于输入参数的位深有所改变。In_a、In_b分别对应列变换的系数和残差的输入,2d_in_a、2d_in_b分别对应行变换的系数和中间值的输入,前端选择器在Count信号的控制下选择输入值进入乘法器。乘法器的输出结果作为加法器的一个输入,加法器的一个输入由上一个结果值作为参数,最初值初始化为0。最后的输出结果由后端选择器控制。
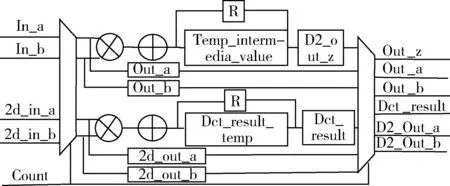
图5 PE单元内部原理图
2.4 控制单元
本设计的控制单元相对比较简单,由一个控制器组成,控制残差数据、系数、中间值,以及何时输入到PE阵列中,何时接收从PE阵列输出的中间值和最后的结果并把它们存入相应的寄存器组中。
2.5 结果转换单元
在HEVC标准中,量化是在整数DCT变换之后,量化的同时会把之前由比例因子放大的倍数给予缩小,因此在变换这一步不做处理。结果转换单元主要负责将最后的DCT变换结果从PE单元中输出并配合控制单元得到整个设计的最终结果。
3 试验结果与分析
3.1 功能仿真结果
研究组PTTG、VEGF-C、VEGFR-3阳性率及LMVD显著高于对照组(P均<0.05)。见表1。
本设计采用Verilog语言对硬件电路进行描述,使用ModelSim10.1d进行功能仿真,在ISE14.2平台上进行综合。本设计针对8×8的残差值做HEVC的整数DCT变换,并在MATLAB上先得到精确结果,表1是原始残差值,表2是在MATLAB上得到的DCT变换结果,图6是在ModeSim中仿真的最终值,对比表2和图6,可以看出两者结果一致,从而证明本设计实现DCT变换功能的正确性。
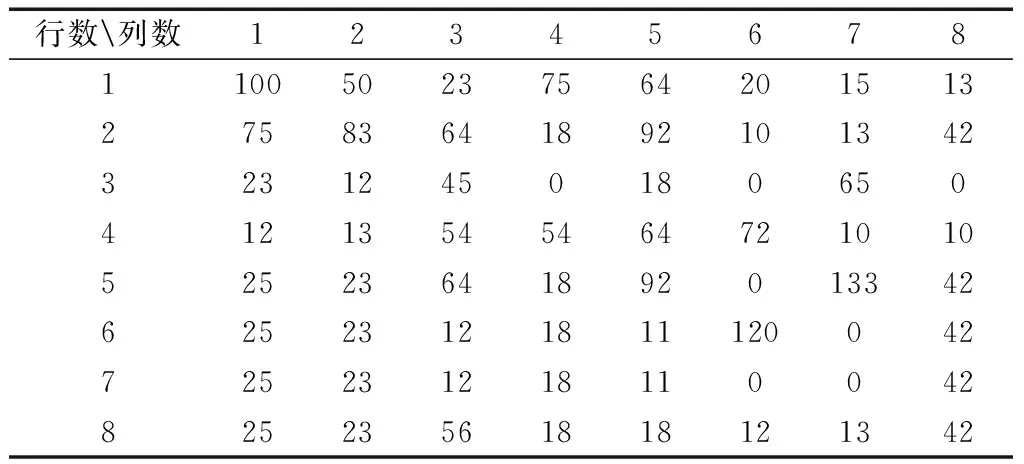
表1 原始残差值在矩阵中位置
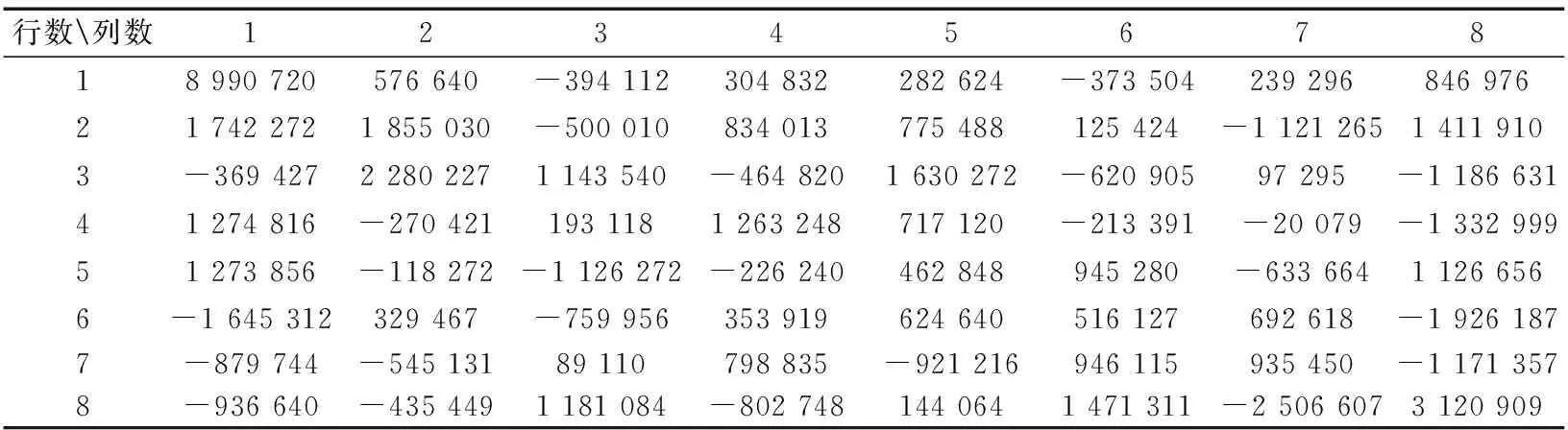
表2 MATLAB计算出的标准结果
3.2 综合结果
在综合时,本文设计采用Xilinx公司生产virtex-6家族的Xc6vlx550t-2ff1759系列芯片,图7所示为综合后的部分RTL图。图中PE00、PE01是实例化出来的2个PE单元,以及它们之间的通信连接。

表3 本文与其他算法的比较
另外文献[6]采用Vivado、LegUp、MATLAB等不同的HLS综合工具对HM15中编写的DCT部分进行了综合,并对每一种尺寸都给出了直接使用乘法器的M模式、使用加法和移位代替乘法操作的AS模式的综合结果。表3列出的是与本文配置最相近的一个对比结果,可以看出本文提出的算法在频率、LUTs、每秒处理帧的数量上都有一定的优势。文献[7]采用无乘法器架构,整个实现方

图6 modesim功能仿真结果
图7 ISE综合结果
式与本文类似,也是先实现列变换,再把结果做一次行变换。但是文献[7]中所用周期数较多,对比文献[7]综合出的结果可知,在主频近似的情况下,本文的周期是它的34%,LUTs是它的62%。
4 结论
本文基于脉动阵列的思想,提出了一个可快速进行DCT变换的框架。算法将DCT变换分解成行列两个独立的一维变换,并且行列变换模块共享硬件资源,其中核心部件PE单元的内部硬件电路也高度对称,这些都使得算法更易于FPGA的实现。在得到列变换的第一个值时便开始将其送入到输入数据处理单元中,经过重组以后的数据再一次被送入PE单元,这之间只要仅仅两个时钟的延迟便可触发开始做行变换,整个框架在控制单元的协同下逐步有序地进行变换,降低了整个变换的周期数目。并且整个算法高度规则,使得最后的工作频率相对较高。此外本文的设计虽是针对HEVC的8×8 DCT变换而实现的,但是却适合于任何的8×8矩阵相乘,因此具有相当高的通用性。
[1] AHMED N, NATARAJAN T, RAO K R. Discrete cosine transform[J]. IEEE Transactions on Computers,1974, c-23(1):90-93.
[2] SULLIVAN G J, OHM J, HAN W J, et al. Overview of the High Efficiency Video Coding (HEVC) standard[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2012, 22(12):1649-1668.
[3] BUDAGAVI M, FULDSETH A, BJNTEGAARD G, et al. Core transform design in the High Efficiency Video Coding (HEVC) standard[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(6):1029-1041.
[4] MEHER P K, PARK S Y, MOHANTY B K, et al. Efficient integer DCT architectures for HEVC[J]. Circuits & Systems for Video Technology IEEE Transactions on, 2014, 24(1):168-178.
[5] AHMED A, SHAHID M U, REHMAN A U. N point DCT VLSI architecture for emerging HEVC standard[J]. Vlsi Design, 2012,2012(2):1-8.
[6] KALALI E, HAMZAOGLU I. FPGA implementations of HEVC inverse DCT using high-level synthesis[C]. Design and Architectures for Signal and Image Processing, IEEE, 2015:2-4.
[7] EDIRISURIYA A, MADANAYAKE A, CINTRA R J, et al. A multiplication-free digital architecture for 16×16 2-D DCT/DST transform for HEVC[C]. Electrical & Electronics Engineers in Israel, 2012:1-5.
[8] OPPENHEIM A V, SCHAFER R W. Discrete-time signal processing[M]. Prentice Hall: Englewood Cliffs, 1989.
Design and implementation of HEVC 8×8 integer DCT based on systolic array
Pan Suwen,Ye Yuhuang,Zheng Mingkui,Chen Zhifeng,Yang Xiuzhi
(School of Physics and Information Engineering, Fuzhou University,Fuzhou 350116, China)
In this paper, based on systolic array to achieve the HEVC(High Efficiency Video Coding) 8×8 integer DCT transform, and to improve the commonly used butterfly algorithm. The overall architecture based on the thought of systolic array can achieve row and column transform synchronization operation, make full use of PE cells, reduce the conversion time and improve the parallelism of FPGA. The designed architecture is not only suitable for DCT transform, but also can be used for any 8x8 matrix multiplication.Finally the synthetical results show that this design can work in the highest frequency of 213.8 MHz.Compared with other algorithms only 35 cycles of time,and less resource cost.The algorithm is very suitable for the real-time requirement of HEVC video image coding, provides a reference for hardware implementation of HEVC encoding standard.
HEVC; DCT; FPGA; systolic array
福建省科技重大专项基金资助项目(2014HZ0003-3);福建省自然科学基金资助项目(2015J01251);福建省教育厅项目(JA14065);福州市科技项目计划资助(2015-G-61)
TN919.81
A
10.19358/j.issn.1674- 7720.2017.09.016
潘苏文,叶宇煌,郑明魁,等.基于脉动阵列的HEVC 8×8整数DCT变换的设计与实现[J].微型机与应用,2017,36(9):53-56,59.
2017-01-10)
叶宇煌(1961-),男,硕士,教授,主要研究方向:数字电视与广播技术、微波通信。
郑明魁(1976-),男,博士,副教授,主要研究方向:视频编码、多媒体通信。

