迎浪状态下内转塔式FPSO船舶运动的短期预报

青兆熹， 卜 佳， 陈武华

(1.中国船级社实业公司湛江分公司, 广东 湛江 524005； 2.上海船舶工艺研究所， 上海 200032)

迎浪状态下内转塔式FPSO船舶运动的短期预报

青兆熹1， 卜 佳2， 陈武华1

(1.中国船级社实业公司湛江分公司, 广东 湛江 524005； 2.上海船舶工艺研究所， 上海 200032)

为预报FPSO在迎浪状态下的运动性能和结构强度，基于频域三维线性势流理论，计算FPSO在规则波中压载、半载、满载3种工况下的响应幅值算子，并对FPSO 3种工况下的运动、加速度和剖面关键载荷进行3 h短期预报。研究结果可为FPSO总体结构强度、疲劳强度和屈曲强度分析提供运动和载荷数据。

FPSO；三维势流理论；频域；短期预报

0 引言

浮式生产储卸油装置(Floating Production Storage and Offloading， FPSO)，是集生产、储油、外输等多种功能于一体的海上浮式油气处理设施。FPSO通常永久系泊于特定海域进行作业，不能像运输船舶那样在遇到恶劣海况时完全避航[1]。

国内外很多学者[2-6]对FPSO在复杂海洋环境作用下的运动特性开展了大量的研究。肖龙飞等[7]采用时域线性三维势流理论，计算了一艘12万吨级FPSO在19.6 m水深中的波频运动，并对其碰底情况进行了研究分析，数值计算结果与模型试验结果吻合较好，说明应用时域计算方法可以从理论上预报FPSO在浅水中的触底情况；FONSECA等[8]采用数值和试验方法研究了北海规则波中极端波浪诱导引起的FPSO垂直弯矩；魏跃峰等[9]通过长达25个月的实测，研究了南海“奋进号”FPSO 6个自由度的运动规律；赵文华等[10]实测获得了台风过境中南海“奋进号”FPSO运动响应数据并对FPSO水动力性能分析数值模型进行了修正；邹佳星等[11]选取某FPSO建立系泊系统耦合计算模型，针对近年极端海洋性气候，应用AQWA-DRAFT与AQWA-NAUT模块，采用时域非线性方法对系泊系统进行耦合分析，评估了影响船体运动的环境参数，给出了系泊钢缆的安全系数。

为了给FPSO船体总体结构强度、疲劳强度、屈曲强度分析提供可靠的运动和载荷数据，本文基于频域三维线性势流理论，计算了FPSO在规则波中压载、半载、满载3种工况下的响应幅值算子，并对FPSO 3种工况下的运动、加速度和剖面关键载荷进行了3 h短期预报。

1 计算方法

1.1 FPSO船体运动响应

物体的运动响应幅值通过刚体运动方程确定：

(1)

式中：ω为波浪圆频率；[M]为物体的质量矩阵；[B]为系统阻尼矩阵；[K]为系泊系统的刚度矩阵；[C]为恢复力矩阵；[a]为附加质量矩阵；[b]为辐射阻尼矩阵；[ξ]为物体运动响应幅值矩阵；[f]为波浪激振力矩阵。由式(1)可求得物体的刚体运动响应幅值。当物体淹没或计算线性小振幅问题时，恢复力矩阵为零。

1.2 波浪力的计算

根据三维绕射-辐射理论计算了湿表面上的水动力载荷。每个绕射单元上的水动压力结果可直接映射到结构模型上进行计算。

流体作用力f可通过瞬时湿表面S上的流体压强积分求得，在一阶近似下有

(2)

式中：fR为频域波浪力结果的实部；fI为频域波浪力结果的虚部。

应用线性化的伯努利方程，上式可写为

(3)

式(3)中第一、二项是入射势和散射势的贡献，定义为激振力：

(4)

辐射阻尼f3由辐射势产生。辐射力(矩)由两部分组成：一部分与浮体的加速度成正比，称为附加质量；另一部分与浮体的速度成正比，称为辐射阻尼：

(5)

式(5)中水动力系数定义为

(6)

式中：aij为附加质量；bij为辐射阻尼。

物体固定不动时的受力为fex；当可以运动时，绕射-辐射共同作用下总的受力为

(7)

1.3 短期预报理论

选择适合FPSO设计作业区域海况的海浪谱计算不规则波海况，常用的海浪谱有Pierson-Moskovitz(P-M)谱、JONSWAP谱等。将幅值响应算子RAO(ω)和波能谱密度SW(ω)采用谱分析的方法计算不规则波中波浪载荷的响应谱：

(8)

式中：SR(ω)为浮体运动或波浪载荷的响应谱；[RAO(ω)]2为幅频特性的平方或响应幅算子的平方；SW(ω)为波能谱密度。

大量实践表明，浮体运动或波浪载荷幅值的短期响应服从Rayleigh分布，即

(9)

式中：x为研究的变量；σ，σ2分别为标准差和方差。

该分布只有方差σ2一个参数可由响应谱SR(ω)得到，即

(10)

此外，可进一步求得短期响应的最大值。短期响应最大值与有义值的关系为

(11)

式中：n为该变量的短期循环次数。

目前3h极值在海洋工程中应用的较多，它是基于90%的可靠性得到的，其表达式为

(12)

确定每个不规则波海况短期预报的极值：

(13)

对每个浪向的不规则波选择最大的短期预报极值和该浪向的幅频响应极值，则该浪向的最大规则波波幅：

(14)

式中：AD为波幅；RAOc为幅频响应极值；LF为随地理环境变化的载荷系数，取值范围为1.1～1.3。

2 实船算例

2.1 计算参数

FPSO船体主要参数见表1。计算工况见表2。

表1 船体主要参数

表2 计算工况

水深100.8 m的环境条件见表3。计算总纵强度时采用百年一遇的海况，考虑锚泊情况时采用十年一遇的海况。

表3 环境条件

模型坐标原点位于自由水面上，x轴指向船头，y轴指向左舷，z轴垂直向上。浪向角为来浪方向与x轴的夹角，即迎浪为180°。船体的湿表面模型如图1所示。由于吃水不同，不同的计算工况湿表面有所不同。

图1 不同工况的湿表面模型

整个FPSO的表面共划分7 266个单元。如图2所示。

图2 不同工况的湿表面模型

质量模型用质量棒进行模拟，不同装载工况的质量模型有所不同。由于船体对称，所以计算0°～180°，步长为15°，共13个浪向角。计算了5～25s，步长1s，共21个周期。采用P-M谱对FPSO进行短期预报。

2.2 计算结果

结合FPSO的水动力性能以及进行总纵强度、屈曲强度和疲劳强度评估的需要，得到了运动RAO、加速度和剖面载荷的短期预报计算结果。由于计算的FPSO为转塔式，所以主要列出了迎浪情况下的结果。图3为迎浪情况下各工况6个自由度方向的运动RAO随频率的变化情况。

图3 迎浪运动RAO结果(浪向角180°)

图4为迎浪情况下，各工况的船体湿表面压力。

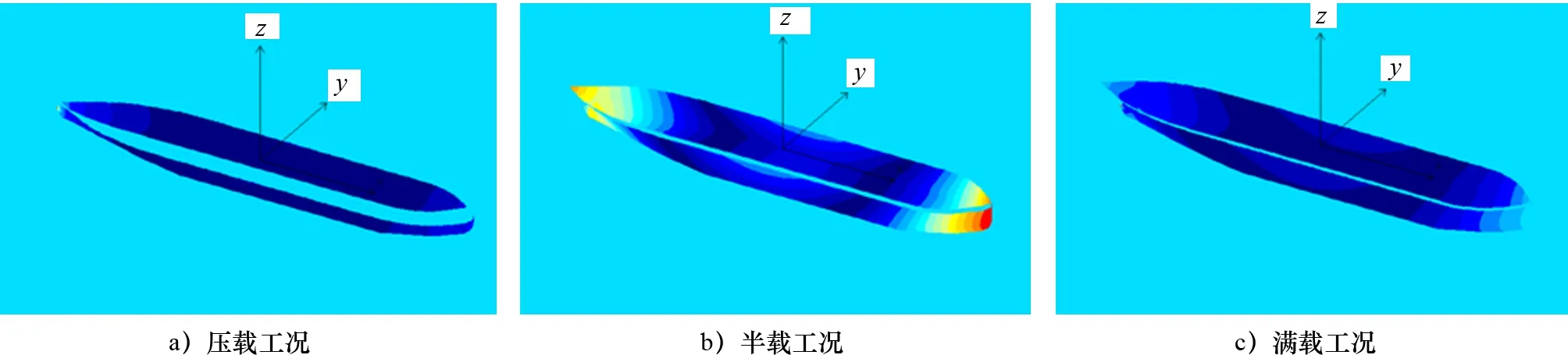
图4 迎浪FPSO表面压力云图(周期25 s)

表4列出了船体坐标原点处的运动短期预报值。

表4 迎浪运动短期预报结果

计算总纵强度和系泊情况下的结构强度采用不同的环境参数。表5和表6分别列出了百年一遇和十年一遇情况下的舱室和船首转塔处的加速度的短期预报值。

表5 迎浪油舱型心处加速度(百年一遇)

表6 迎浪艏部转塔区的垂向加速度短期预报结果(十年一遇)

图5和图6分别为迎浪情况下，各工况沿船长方向剪力和弯矩的短期预报值。

图5 迎浪剪力短期预报结果

图6 迎浪弯矩短期预报结果

由计算结果可以看出：

(1) 在迎浪压载工况下，FPSO平台纵荡的最大幅值为5.13 m，垂荡的最大幅值为4.29 m，纵摇的最大幅值为0.106 7 rad，剪力最大值8.301 4×107N，弯矩最大值5.5967×109N·m。

(2) 在迎浪半载工况下，FPSO平台纵荡的最大幅值为4.06 m，垂荡的最大幅值为4.31 m，纵摇的最大幅值为0.097 6 rad，剪力最大值1.041 8×108N，弯矩最大值6.464 3×109N·m。

(3) 在迎浪满载工况下，FPSO平台纵荡的最大幅值为3.95 m，垂荡的最大幅值为4.52 m，纵摇的最大幅值为0.093 5 rad，剪力最大值1.028 2×108N，弯矩最大值6.793 3×109N·m。

该计算结果可为FPSO总体结构强度、疲劳强度和屈曲强度的分析和校核提供参考。

3 结论

为预报FPSO船舶在迎浪状态下的运动性能和结构强度，建立了三维湿表面模型和质量模型。基于频域三维线性势流理论，分析和计算了FPSO的压载、半载、满载3种工况下的响应幅值算子，并对FPSO 3种工况下的运动、加速度和剖面关键载荷进行了3 h短期预报。研究结果可为FPSO总体结构强度、疲劳强度和屈曲强度分析提供运动和载荷数据。

[1] 肖龙飞, 杨建民. FPSO水动力研究与进展[J]. 海洋工程, 2006, 24(4):116-123.

[2] 莫建, 康庄, 曾骥,等. 多点系泊FPSO截断设计及其总体响应分析[J]. 中国海洋平台, 2014, 29(6):35-40.

[3] 吴家鸣. FPSO的特点与现状[J]. 船舶工程, 2012(S2):1-4.

[4] 肖龙飞, 杨建民, 胡志强. 极浅水单点系泊FPSO低频响应分析[J]. 船舶力学, 2010, 14(4):372-378.

[5] FONTAINE E, ORSERO P, LEDOUX A, et al. Reliability Analysis and Response Based Design of a Moored FPSO in West Africa[J]. Structural Safety, 2013, 41(3):82-96.

[6] SOHN J M, SANG J K, KIM B H, et al. Nonlinear Structural Consequence Analysis of FPSO Topside Blastwalls[J]. Ocean Engineering, 2013, 60(1):149-162.

[7] 肖龙飞, 杨建民, 李欣. 浅水区FPSO波频运动与触底时域分析[J]. 中国海洋平台, 2009, 24(2):33-36.

[8] FONSECA N, PASCOAL R, SOARES C G, et al. Numerical and Experimental Analysis of Extreme Wave Induced Vertical Bending Moments on a FPSO[J]. Applied Ocean Research, 2010, 32(4):374-390.

[9] 魏跃峰, 杨建民, 陈刚,等. FPSO运动实测数据统计研究——“南海奋进号”FPSO实船测量研究Ⅰ[J]. 海洋工程, 2011, 29(3):96-101.

[10] 赵文华, 胡志强, 杨建民,等. FPSO系泊系统载荷计算与分析——基于南海"奋进号"FPSO运动特性实船测量结果[J]. 中国海上油气, 2011, 23(2):116-121.

[11] 邹佳星, 任慧龙, 李陈峰. 极端海况下FPSO系泊系统安全性评估与分析[J]. 哈尔滨工程大学学报, 2015(1):104-108.

Short-Term Prediction of Internal Turret FPSO Motion in Head Waves

QING Zhaoxi， BU Jia， CHEN Wuhua

(1.Zhanjiang Branch of China Classification Society Industry Corp., Zhanjiang 524005, China；2.Shanghai Shipbuilding Technology Research Institute, Shanghai 200032， China)

In order to predict the movement performance and structural strength of FPSO, the amplitude operator of response (RAOs) is calculated under ballast, half load and full load conditions respectively in regular waves based on 3D potential theory. Three hours of short-term prediction of motion, acceleration and main profile stress is performed under different load cases. The data of motion and load is applied to the analysis of structural strength, fatigue strength and buckling strength.

FPSO； 3D potential theory； frequency domain； short-term prediction

2016-04-06

青兆熹(1981-)，男，工程师

1001-4500(2017)02-0088-07

P751

A