近海风电机结构动力响应极值预报

王立夫

(上海海事大学 物流工程学院， 上海 201306)

近海风电机结构动力响应极值预报

王立夫

(上海海事大学 物流工程学院， 上海 201306)

鉴于国内外在预报风浪共同作用下近海风电机的极限结构动力响应方面仍然面临挑战的现状，提出用最小二乘法高效精确地求解广义柏拉图分布中的待定参数，预报某5 MW漂浮式风电机塔筒平台接合处的前后向弯矩极值，并用蒙特卡罗仿真和诊断图证明了最小二乘法与传统的矩方法相比的优越性。可为浮式海上风电机的结构设计提供参考。

近海漂浮式风电机；弯矩；最小二乘法；矩方法；蒙特卡罗仿真

0 引言

风电是一种清洁、绿色的可再生能源。据估计, 到2020年中国风电装机容量有望达到3亿kW左右[1]。与陆上风能相比，近海风能具有风速高、稳定、靠近人口密集区、机组利用率高、不占用陆地面积和受噪声标准限制小等显著优点, 是风电发展的重要方向[1]。近海风电机可利用丰富的近海风能资源发电，无污染。近年来随着风电技术的发展, 欧美地区的近海风电开发步伐日益加快，已进入了商业化应用阶段。然而，在进行近海风电机结构设计的过程中，风浪共同作用下极限结构动力响应的预报仍然面临挑战[2]。

在预报近海风电机的结构动力响应极值时，对于特定的环境状态，一般是基于已有数据获得风电机短期结构动力响应极值的概率分布，再对所有环境状态下的短期响应极值分布积分，得出一个长期分布，并根据该长期分布计算出对应于某回归周期的长期结构动力响应极值。由此可见，精确预报风电机短期结构动力响应极值的概率分布，对于计算风电机的长期响应极值至关重要。本文主要研究如何精确预报风电机短期结构动力响应极值的概率分布，为长期结构动力响应极值的预报奠定基础。

在美国国家可再生能源实验室的经典报告[3]中,作者用矩方法计算了两个1.5 MW风电机在不同风况下的短期响应极值分布，并指出：“后续的工作应该着眼于研究用矩方法预报变桨距风电机短期响应极值分布的不足之处”，说明矩方法不是预报风电机短期响应极值分布的最佳方法，有必要寻求新的预报方法。

我国的近海风场潜力巨大，据中国风能协会以及世界自然基金会的估算，我国在离海岸线100 km,中心高度100 m的范围内， 7 m/s以上风力的潜在发电能力为年均110万亿kW。目前，美国、中国、日本、挪威和世界其他国家的近海风场潜能中的大部分位于水深大于30 m的海面上。在浅水区域(水深0～20 m)固定式单桩风电机比较适用；在过渡区域(水深30～50 m)三角架或导管架式风电机比较适用；而在深水区域(水深50～300 m)，浮式海上风电机是最经济的机型。

本文针对海上漂浮式风力发电机模型作进一步深入的研究[4-7]，应用FAST软件对某一5 MW漂浮式风电机塔筒平台接合处的前后向弯矩进行仿真，得到弯矩响应时间历经，对其中高于某一标准门槛值的各个峰值用广义柏拉图分布渐近(进而可转化为广义极值分布)。用最小二乘法[8]求解广义柏拉图分布中的待定参数，预报该漂浮式风电机塔筒平台接合处的前后向弯矩极值，并用蒙特卡罗仿真和诊断图证明最小二乘法与传统矩方法相比的优越性。在保证浮式风机结构强度的前提下，可使建造风机耗费的结构材料最省，以获得最优的经济效益。

1 理论背景

1.1 广义柏拉图分布和广义极值分布

近海风电机设计要求中推荐采用统计外推预报风电机在极限状态下的结构动力响应，对应于超越概率QT的风电机长期响应lT[2]

(1)

式中：fx(x)是各环境随机变量X的长期联合概率密度[9]；L是响应随机变量；Q[L|X=x]是一特定X条件下的短期超越概率分布。

对近海风电机，环境随机变量X由轮毂高度处的平均风速V和有义波高Hs组成。对于特定环境X=x,首先求解该环境下风电机响应的短期超越概率分布Q[L|X=x]。

本文应用FAST软件得到某5MW漂浮式风电机塔筒平台接合处前后向弯矩响应的时间历程，从中取出N个高于IEC标准门槛值的响应峰值Lr(r= 1, 2, …，N)， 这N个峰值可用广义柏拉图分布(GPD)渐近(进而可转化为广义极值分布)。

利用1.2.1中获得cDNA，采用实时荧光定量PCR仪(Eppendorf，德国)进行候选基因时空表达水平分析。选取的内参基因为BnACTIN2，实验中检测的基因为BnCPD、BnDWF4、BnDET2、BnBRI1、BnBIN2和BnBZL2。实验所用引物序列见表1。

(2)

式中：c和a为待定参数。

为求短期极值分布的关键是求广义柏拉图分布中的待定参数c和a。用传统的矩方法求广义柏拉图分布中的待定参数时包含对抽样观查值的平方运算，如果抽样值中包含奇点(不切实际的特大值)，那么抽样误差将被放大。

1. 2 最小二乘法

用最小二乘法求广义柏拉图分布中的待定参数c和a是通过n个样本离差的平方和最小化来实现的，n个样本离差的平方和[9]为

(3)

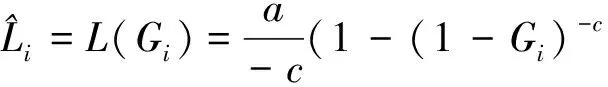
使S对c和a的偏导数等于零，就可得出c和a的表达式。

2 计算实例

图1 NREL 5 MW OC3-Hywind 浮式风电机

风电机动力响应仿真FAST软件是美国国家风能中心应用FORTRAN语言研发的气动载荷分析软件，可以计算风机响应及疲劳。参照IEC 61400-3的设计要求，对美国国家可再生能源实验室开发的一种典型近海风电机——NREL 5 MW OC3-Hywind 浮式风电机进行仿真，得到其短期响应数据集合。该浮式风电机如图1所示，主要参数见表1[7]。

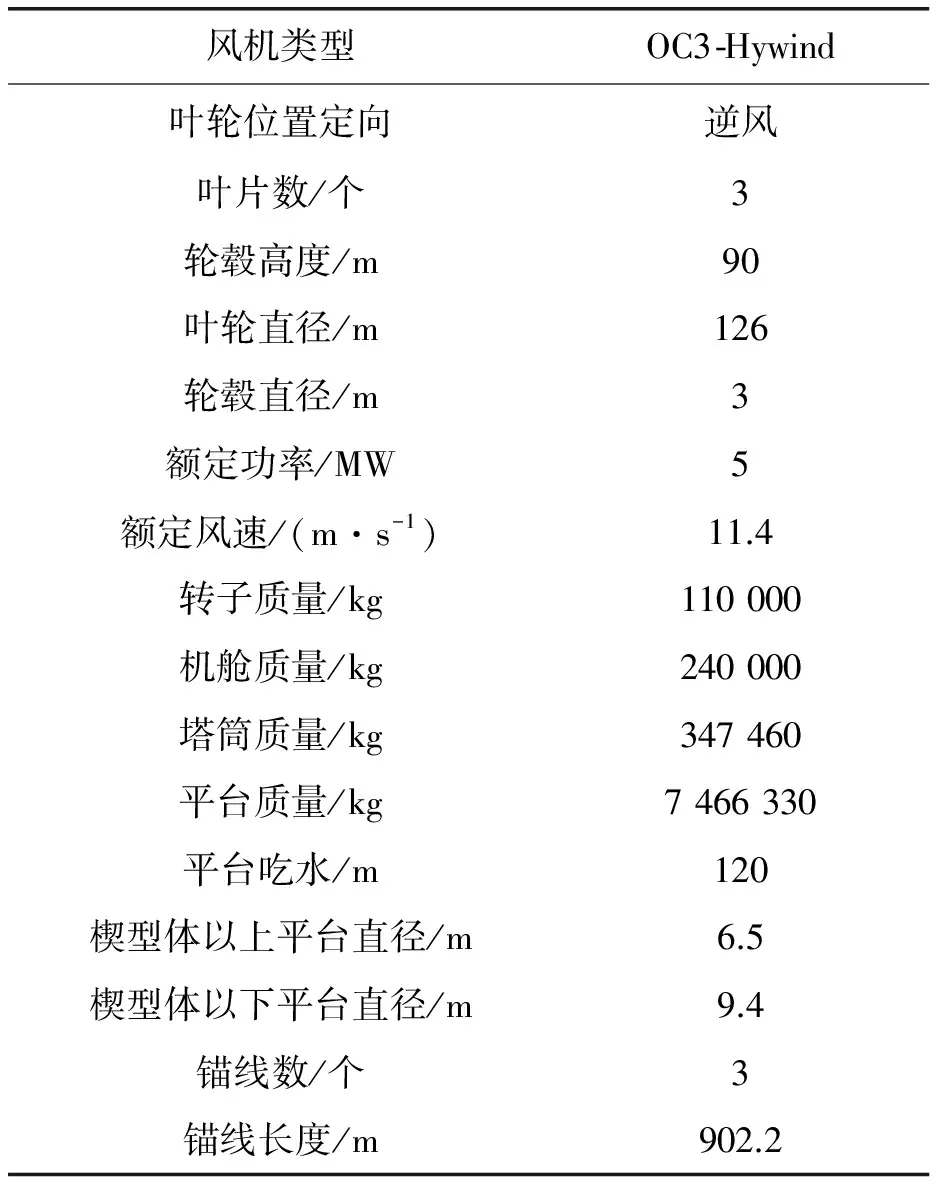
表1 NREL 5 MW OC3-Hywind 浮式风电机的主要参数

为统计外推出塔筒平台接合处的前后向弯距，根据设计方案应用FAST软件仿真，得到输出out文件中的TwrBsMyc1参数。外推第一步的关键是得到塔筒平台接合处前后向弯矩的短期分布。首先,对NREL 5 MW OC3-Hywind 浮式风电机应用NWTC研发的TURBSIM软件和FAST软件进行仿真得到响应数据。其次，应用TURBSIM软件对不同风随机数下的风机流入风进行仿真，生成相应的紊流风bts风文件，将其放入FAST风数据中与输入文件关联，同时修改FAST源文件中平台输入文件的波浪随机数WaveSeed(1)和WaveSeed(2)，运行FAST软件，最终生成仿真10.5 min的输出out文件。塔筒平台接合处前后向弯矩在10.5 min(去掉前0.5 min)内的时间历经如图2所示。

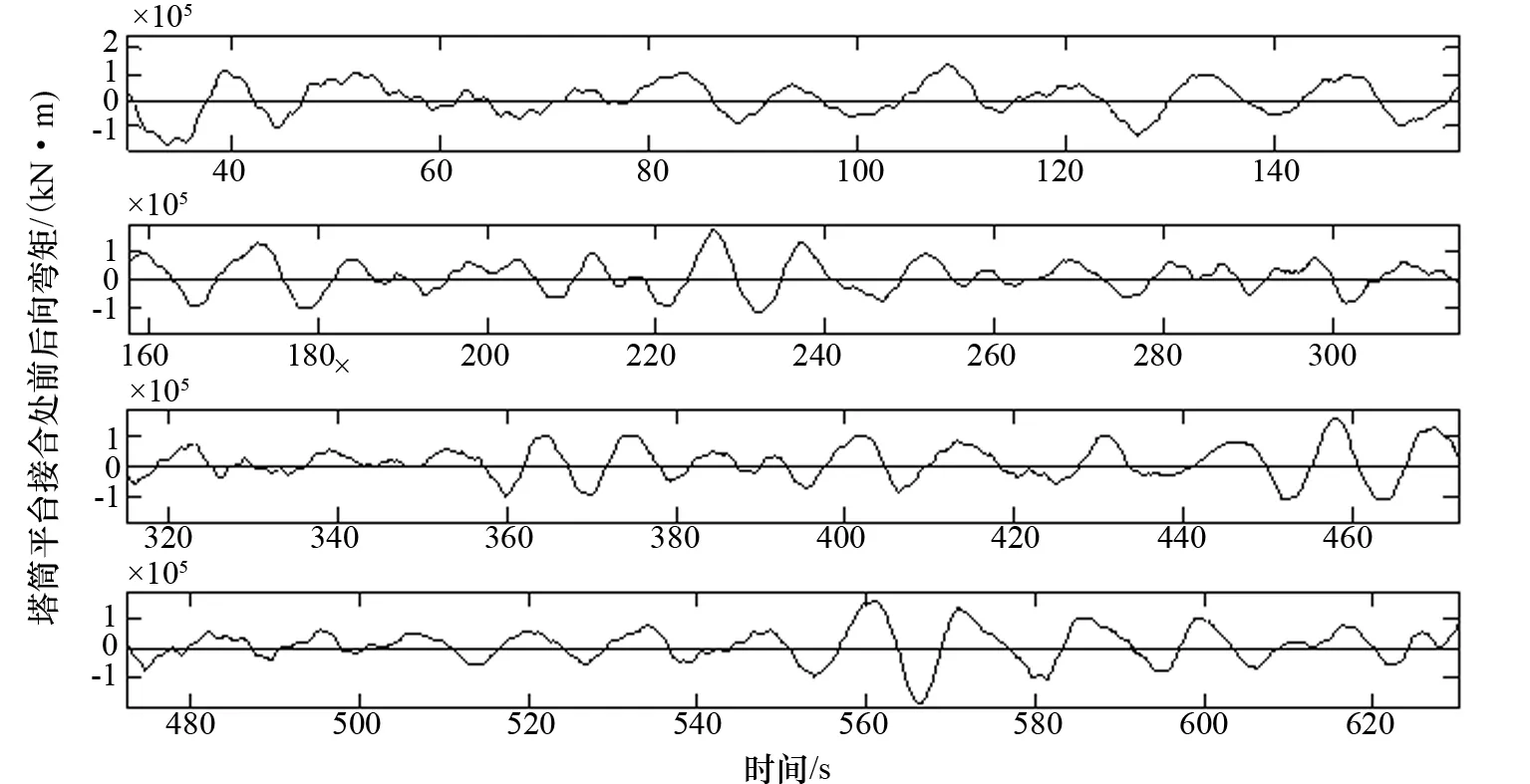
图2 塔筒平台接合处前后向弯矩的10 min时间历经

采用不同的风与波浪随机数仿真20组，计算得到塔筒平台接合处前后向弯矩的20组10 min时间历经，将它们接合起来就得到一个200 min的弯矩时间历经。将这200 min的弯矩时间历经排序，得到弯矩最大值为226 000 kN·m, 此数值即为用蒙特卡罗仿真得到塔筒平台接合处的前后向弯矩的短时(200 min)极值。

2.2 计算得到的响应极值和响应极值概率分布

开发了一套MATLAB程序执行第1节中的方法，计算对象是200 min弯矩时间历经。按照国际电工委员会(IEC)2009年颁布的“近海风电机设计要求”，取标准门槛值等于该200 min时间历经的均值加1.4倍标准差,计算得到门槛值为88 228 kN·m。接着，用MATLAB程序抽取该200 min时间历经中高于门槛值的各个峰值(即抽样值)，将广义柏拉图分布拟合到抽样值上。其中，广义柏拉图分布中的待定参数c和a用最小二乘法(求得a=321 630，c= -2.332 9)和矩方法(求得a= 1 043 200,c= -8.612 3)分别求出。2种方法得到的广义柏拉图分布概率密度图和诊断图如图3和图4所示。

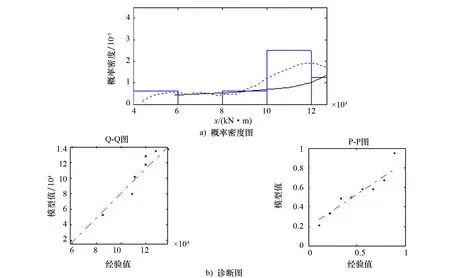
图3 用最小二乘法求得的广义柏拉图分布的概率密度图和诊断图

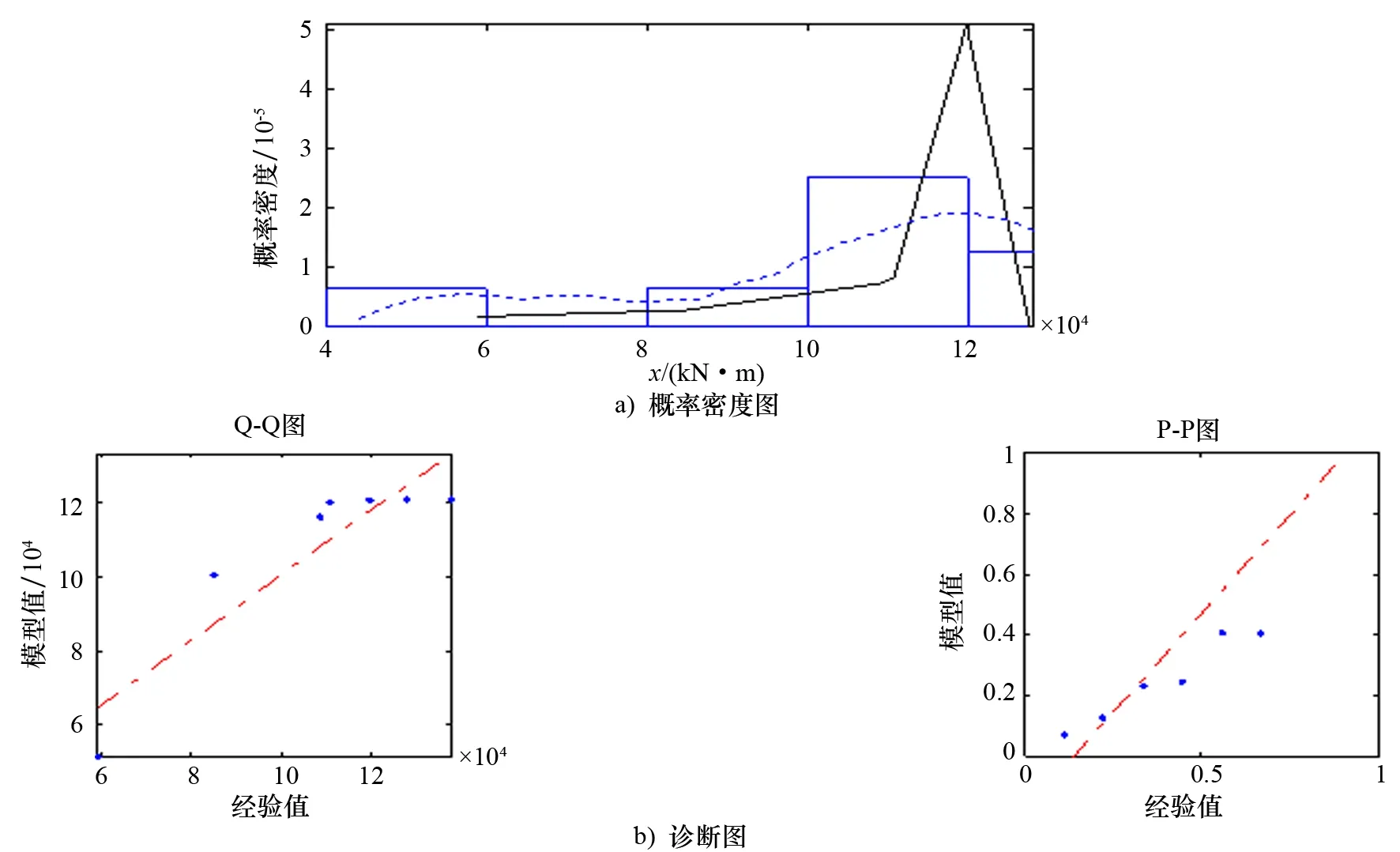
图4 用矩方法求得的广义柏拉图分布的概率密度图和诊断图

在图3和图4中的概率密度图中，经验(即抽样值)分布用直方图表示，直方图的趋势用虚线表示，拟合的广义柏拉图分布用实线表示。图3中虚线和实线拟合度较图4好，说明用最小二乘法拟合的短期极值分布求解响应的长期极值更精确。

在图3和图4中也包括了诊断图，即Q-Q图和P-P图。图3中的Q-Q图中，点比较均匀地分布在45°倾角的点划线两边，说明用最小二乘法拟合的广义柏拉图分布更接近抽样值。图4中的Q-Q图中的点很发散地分布在45°倾角的点划线两边，说明用矩方法拟合的广义柏拉图分布远离抽样值。在图3和图4中的P-P图中也可观察到同样的趋势。

将塔筒平台接合处前后向弯矩200min时间历经极值的数学期望与用蒙特卡罗仿真得到的极值进行比较，见表2。由表2可知，在预报漂浮式风电机短期载荷极值时，最小二乘法与传统的矩方法相比，更具优越性。

表2 计算求得塔筒平台接合处的前后向弯矩的200 min时间历经的极值

3 结语

本文提出用最小二乘法求解广义柏拉图分布中的待定参数，预报漂浮式风电机塔筒平台接合处的前后向弯矩极值，并用蒙特卡罗仿真和诊断图证明了最小二乘法与传统的矩方法相比的优越性。该方法可用于优化设计该型风电机塔筒平台接合处的剖面属性(剖面形状、面积大小，剖面模数、材料选取等)，在保证海上浮式风电机结构强度的前提下，可使建造风电机所耗费的结构材料最省，以获得最优的经济效益。本文所提出的新方法可为风能领域的工程师研发设计新型风电机(海上或陆基)提供参考。

[1] 郑崇伟,潘静.全球海域风能资源评估及等级区划[J]. 自然资源学报, 2012，27(3):364-371.

[2] AGARWAL P, MANUEL L. Simulation of Offshore Wind Turbine Response for Long-term Extreme Load Prediction [J]. Engineering Structures, 2009, 31(10): 2236-2246.

[3] MORIARTY P J, HOLLEY W E，BUTTERFIELD S P. Extrapolation of Extreme and Fatigue Loads Using Probabilistic Methods [R]. Technical Report, 2006.

[4] JONKMAN J M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine [R]. Technical Report, 2007.

[5] JONKMAN J M, MATHA D. A Quantitative Comparison of the Responses of Three Floating Platforms [C]// Presentation at European Offshore Wind 2009 Conference and Exhibition, Stockholm, Sweden, 2009.

[6] KARIMIRAD M, MOAN T. Extreme Dynamic Structural Response Analysis of Centenary Moored Spar Wind Turbine in Harsh Environmental Conditions [J]. Offshore Mechanics and Arctic Engineering, 2011，133: 1-14.

[7] SAMUELSSON L, YU Q. A New Footing-Analyzing the Viability of Floating Offshore Wind Turbines [J]. Marine Technology, 2012: 22-25.

[8] 王穗辉. 误差理论与测量平差[M]. 上海： 同济大学出版社，2010 ．

[9] JOHANNESSEN K, MELING T S， HAVER S. Joint Distribution for Wind and Waves in the Northern North Sea [C]// Proceedings of the International Offshore and Polar Engineering Conference, Stavanger, Norway, 2001.

Prediction of Structural Dynamic Response Extreme Values of Offshore Wind Turbine

WANG Lifu

(Logistics Engineering College, Shanghai Maritime University, Shanghai 201306， China)

Due to the fact that it is still a challenge at both home and abroad on how to predict the extreme structural dynamic responses of an offshore wind turbine under the concurrent action of wind and waves, the method of least squares is used to more efficiently and accurately estimate the unknown parameters in the Generalized Pareto distribution so that the extreme values of the fore-aft bending moments at the tower-Spar interface of a 5 MW floating wind turbine are predicted. Monte Carlo simulation and diagnostic plots are used to test the advantages of the method of least squares over the traditional method of moments. The new method proposed will become a powerful tool for the people in their structural design of a floating offshore wind turbine.

offshore floating wind turbine; bending moment; method of least square; method of moments; Monte Carlo simulation

2016-03-30

王立夫(1996-)，男，本科生

1001-4500(2017)02-0055-05

TK83

A