基于拼接重构的长导轨直线度测量方法*

钱林弘,吕 磊,夏 欢

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

基于拼接重构的长导轨直线度测量方法*

钱林弘,吕 磊,夏 欢

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

为了有效解决超精密设备长导轨全行程直线度精确测量的难题，文章提出了一种基于拼接重构原理的测量方法。首先采用激光干涉仪对短基准平晶面形误差进行测量，并用于补偿到长导轨直线度测量结果；接着比较了不同倾斜误差消除方法的效果，并确定消倾斜误差的优选方法；然后分析了拼接重叠长度、拼接次数以及环境噪声对测量结果的影响规律；最后对金刚石飞切机床的超精密长导轨开展直线度测量，并将测量结果与采用长平晶测量结果进行对比。结果表明：两者的误差在15.8%以内，有效验证了文中提出的拼接重构方法的有效性，为解决超精密设备长导轨全行程直线度测量提供了一种新的思路。

超精密；长导轨；拼接；直线度；误差

0 前言

随着制造业的快速发展，超精密加工技术发挥着日益重要的作用。静压导轨具有运转平稳、精度高、摩擦小、使用寿命长等优点，因此在超精密加工机床得到广泛使用。静压导轨作为超精密切削机床的主要运动功能部件，其直线度误差将显著影响超精密加工精度[1-3]。目前通常采用提高导轨超精密研磨精度、误差补偿[4-6]等方法降低导轨直线度误差对加工精度的影响，而导轨直线度的准确测量是提高研磨精度和误差补偿的基础。因此开展超精密长导轨直线度测量对于提高超精密加工精度，促进超精密技术发展具有显著意义。

目前，导轨直线度的测量主要采用电子水平仪法[7]、自准直仪法[8]、双频激光干涉法[9]和测微法[10]等。其中电子水平仪操作简单、使用方便、成本低廉，但是精度较低，普遍精度为20μm/m，数据采集和整理较难；且由于水平仪的跨距问题，主要应用测量较短导轨垂直面直线度。自准直仪的精度比水平仪测量法高，最高精度为5μm/m；随着测量范围增加，测量偏差逐渐增大，主要应用中等长度导轨直线度测量。激光干涉仪的测量距离大，测量精度可达到0.2μm/m，可连续测量和采用微型计算机进行数据处理，主要应用于较高精度长导轨直线度测量。但采用激光干涉仪测量直线度，每次测量采点时导轨需定点停止运动并保持稳定，不能在运行过程中采点，测点较多时，随测量时间的加长，引入的环境等影响因素增大，自身抗干扰能力低，导致测量误差较大[11-12]。短基准平晶：测量距离短，测量精度高，可达0.1μm/200mm，可在导轨运行中连续测量和采用微型计算机进行数据处理，抗干扰能力强、价格相对激光干涉仪较低，主要应用在高精度短导轨直线度测量中。目前国内超精密加工机床直线导轨行程已经达到500mm～ 2000mm，其精度达0.1μm～0.2μm/500mm～ 2000mm。因此现有方法较难实现超精密长导轨直线度的准确测量。

为了实现长导轨全行程直线度的精确测量，本文提出了一种基于拼接重构原理的测量方法。首先采用激光干涉仪对短基准平晶面形误差进行测量，并将其补偿到长导轨直线度测量结果中；接着比较了不同倾斜误差消除方法的效果，并确定消倾斜误差的优选方法；然后分析了拼接重叠长度、拼接次数以及环境噪声对测量结果的影响规律；最后对超精密长导轨开展直线度测量，并将测量结果与采用长平晶测量结果进行对比。

1 基于短平晶的导轨直线度拼接测量方法

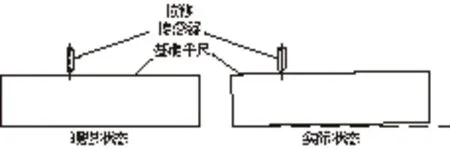
本文采用一维拼接重构的方式，将超精密设备长导轨划分为具有一定重叠区域的数段较短导轨，再通过算法将各段导轨直线度误差轮廓拼接起来，获得超精密设备长导轨直线度。拼接原理示意图如图1所示，两段曲线拼接的充要条件是在拼接点处具有相等的数值和切线斜率。但是在测量过程中，由于短基准平晶未经调平处理，当将短基准平晶放置于工作台后，平晶的下底面与工作台表面接触，会导致短基准平晶上表面产生倾斜，进而对测量结果引入直线趋势项。同时，测量结果中混入了平晶自身的面形精度、多次测量不共线等误差源，因此需要在实际测量中，考虑到噪声、振动、温度等环境因素、拼接的重叠区域，重叠区域的长度和拼接次数对测量结果的影响。

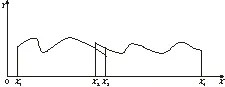
图1 拼接原理示意图

(1)

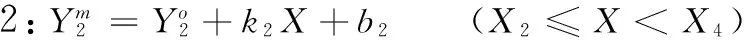
(2)

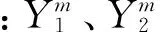
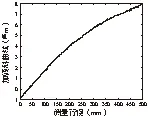
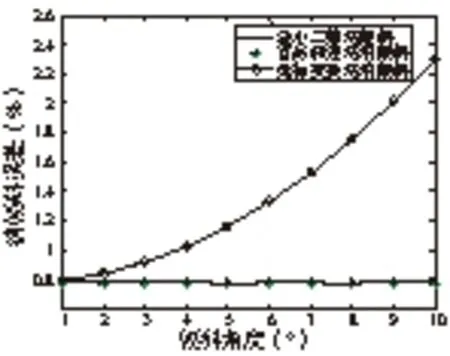
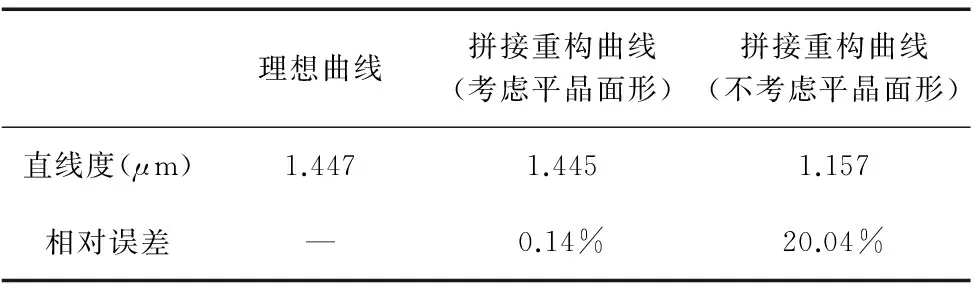
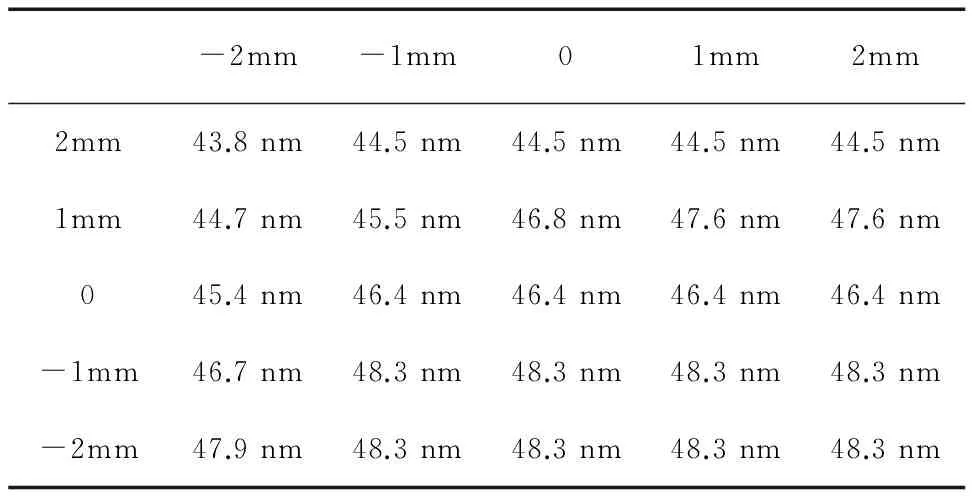
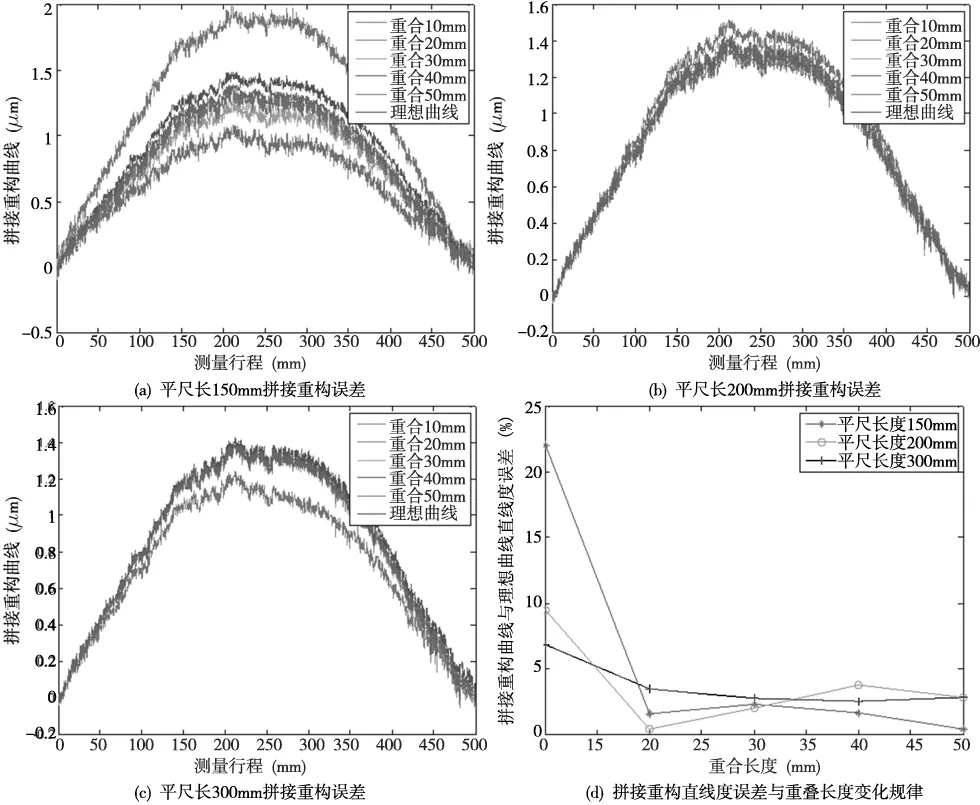
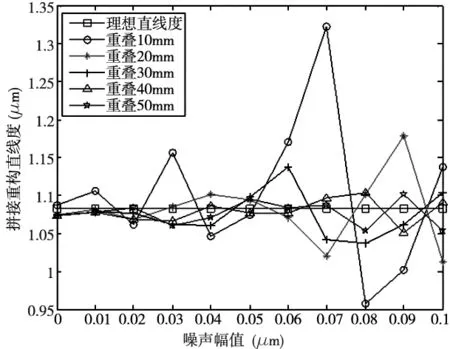
ΔYm=ΔkX+Δb(X2≤X

(3)

2 测量算法仿真分析

拼接测试方法中的数据处理比较复杂，包括短基准平晶面形补偿、平晶的消倾斜、平晶移动时导致多次测量不共线、拼接重构时重叠部分的长度及拼接次数、以及测量过程中的去噪声等。

2.1 短平晶消倾斜算法仿真分析

采用平晶测量时，由于机床床身等基准的原因，导致平晶放置时存在一定倾斜，一般采用调平机构将平晶调整至理想状态，但采用短平晶拼接时，每次调平会增加整体测量的时间，导致环境影响增加，因此，在拼接中采用消倾斜算法将实际测量状态中的倾斜消除，保证测量起始和终止的数据相等，即消除倾斜后相当于测量中平晶放置的理想状态，如图2所示。

图2 平晶消倾斜示意图

短平晶消倾斜时可采用最小二乘法、首尾连线法、坐标变换法，提取一组长平晶测量结果数据作为理想曲线(直线度为1.447μm)，如图3所示，并在理想曲线中加入有一定斜率的曲线和噪声(如图4)，通过对比三种消倾斜方法后得到的直线度与理想直线度之间的误差(如图5、图6)，可以发现：噪声一定，随着倾斜角度的增大，采用坐标变换法消倾斜误差随之增大，而首尾连线法与最小二乘法消倾斜误差并不随倾斜角度的增大而增大；倾斜角度一定，随着噪声赋值的增大，采用三种消倾斜方法所得的消倾斜误差随之增大，但三种方法之间消倾斜误差相差不大。由此可得，测量过程中可选择最小二乘法或首尾连线法进行消倾斜处理，并控制环境噪声，或采取滤波算法对测量数据进行后处理。

图3 理想曲线

图4 加倾斜曲线

图5 噪声一定，不同倾斜角度下消倾斜误差

图6 倾斜角度一定，不同噪声幅值下消倾斜误差

2.2 短平晶面形补偿算法仿真分析

短基准平晶本身具有一定的面形，一般可以达到30-60nm，当被测导轨精度较低时，可忽略短基准平晶面型精度对测量结果的影响，但对于所测高精度导轨的直线度，短基准平晶面型与导轨直线度为同一数量级，需对短基准平晶的面形进行误差分离。其误差分离可采用两种方法：一是采用单尺反转法将被测直线和参考直线的直线度误差分离。二是采用激光干涉仪测量短基准平晶的面形，通过提取其面形上被测部分的直线度，获取基准的直线度数据，再通过反向误差补偿技术，将短基准平晶的数据补偿到测量结果中，从而消除短基准平晶引入的误差，本文采用第二种方法。

平晶测量结果如图7所示，其面形精度为0.0464μm，整体趋势为凹心，对拼接4次的仿真数据分别反补入平晶的面形结果，再将4组数据拼接，最后得到消除平晶面形影响的拼接直线度与原未考虑平晶面形影响直线度的结果(如图8)，数值结果如表1所示，理想曲线直线度为1.447μm，补偿前平尺面形拼接重构曲线直线度为1.445μm，与理想曲线直线度相对误差为0.14%；补偿后平尺面形拼接重构曲线直线度为1.157μm，与理想曲线直线度相对误差为20.04%。因此，由平晶面形引入的误差较大，在数据处理时，应该进行补偿。

图7 平晶面形

图8 平晶面形补偿前后的曲线直线度

理想曲线拼接重构曲线(考虑平晶面形)拼接重构曲线(不考虑平晶面形)直线度(μm)1.4471.4451.157相对误差—0.14%20.04%

2.3 短平晶移动的测量不重叠仿真分析

导轨直线度拼接过程中，由于移动短基准平晶，每次移动后测量平晶会与原测量基准直线相差1～2mm，因此需分析短基准平晶被测区域的面形精度情况，针对中间的平晶直线，分别向前后和左右各移动1mm、2mm，得到一组平晶的面形值，如表2所示，误差=最大值-最小值=(48.3-43.8)=4.5nm。而总体直线度为1.447μm，因此，平移对测量结果影响为0.31%，可忽略不计。

表2 平晶平移造成的测量误差

2.4 短平晶测量重叠长度和拼接次数仿真分析

两段曲线的拼接重叠部分的算法采用最小二乘法，其拼接重叠长度和拼接次数会影响拼接结果。首先，对理想曲线(长500mm，PV=1.447μm)按表3对应关系进行拆分，并加入幅值为0.01的随机噪声。在不同重叠长度和拼接次数仿真实验中，验证拼接算法的最小二乘法数据处理误差，并同时获得拼接中的重叠长度和拼接次数对测量结果的影响，实验结果如图9。

表3 不同平尺长度下重叠长度和拼接次数对应关系

图9 拼接曲线与直线度随重叠长度变化规律

由图9可以看出，平尺长度为300mm时，拼接次数最少，从而由拼接次数带来的累计误差最小，因此拼接重构直线度误差整体最小；当重叠长度>20mm时，拼接重构误差趋于稳定，当重叠长度<20mm时，噪声对拼接曲线段影响较大，导致拼接重构误差变大。因此，进行拼接测量时应综合考虑拼接次数和重合长度对直线度误差的影响，折中选择相应的拼接次数和重叠长度。

2.5 短平晶测量去噪声仿真分析

在实际测量中，测量噪声为一个干扰源，会对测量结果造成影响。设定理想曲线(PV=1.083μm)，测量过程中会有噪声引入的误差，当噪声逐渐增大时，其拼接长度不同，对拼接结果影响也不相同，具体情况如图10、图11所示，从图中可以看出随着噪声增加，重叠长度在10mm时，外界噪声对直线度拼接结果影响较大，重叠长度在大于30mm后对直线度拼接结果的影响并不明显，因此，在测试中必须严格控制噪声影响，且拼接的重叠部分长度应大于等于30mm。

图10 拼接重构直线度与噪声幅值变化规律

图11 拼接重构误差与噪声幅值变化规律

3 高精度长导轨直线度测试

利用拼接测量原理及数据处理算法，对超精密飞切机床中的高精度气浮导轨直线度误差进行了测量。测量中使用TT80位移传感器进行直线度轮廓采样(点间距0.1mm)。分4段进行测量，图12为拼接测量实验现场图，系统主要由TT80位移传感器、短基准平晶、数据采集系统及数据处理软件组成。

拼接测量实验结果如图13所示，气浮导轨500mm行程内直线度误差PV平均值为1.737μm。由图中各条拼接曲线可知，实验结果具有很好的重复性；同时，为验证拼接测量结果的正确性，采用500mm长基准平晶进行全长测量，六次测量结果的平均值为1.500μm，同前述拼接测量结果1.737μm的误差为15.8%，表明了拼接测量方法的正确和有效性。

图12 拼接实验现场

图13 拼接测量实验结果

4 结论

由于检测仪器和方法的限制，目前无法实现超精密设备长导轨全行程直线度的检测。本文首先提出基于拼接重构的思想，采用短平晶拼接测量长导轨直线度；其次，详细分析了拼接过程中短基准平晶倾斜和面形、重叠长度和拼接次数、以及测量过程中的噪声的影响，并通过仿真分析各因素对测量结果的影响，进行误差分离和补偿提高测量精度；最后，通过对超精密飞切机床的500mm长高精度气浮导轨直线度进行了测量。实验结果表明：采用短平晶拼接测量直线度为1.737μm，与长基准平晶进行全长测量结果1.500μm相比较，其测量误差为15.8%，验证了拼接测量方法的正确和有效性。同时，通过短平晶拼接测量可获得全频段直线度形貌，从而可实现导轨直线度的定量调节和机床导轨直线度误差补偿控制，进而将有效提升机床导轨的直线度精度。

[1] 胡秋,夏仰球,米良,等.超精密静压支承部件及其在超精密加工机床的应用[J].机床与液压,2015, 43(22):4-7.

[2] 梁迎春,陈国达,孙雅洲,等.超精密机床研究现状与展望[J].哈尔滨工业大学学报,2014,46(5):28-39.

[3] 牛景丽,陈东海.现代超精密加工机床的发展及对策[J].机床与液压,2010,38(2):94-97.

[4] Weichert C, Bosse H, Flügge J, et al.Implementation of straightness measurements at the Nanometer Comparator[J]. CIRP Annals-Manufacturing Technology, 2016, 65(1):507-510.

[5] Liu C H, Jywe W Y, Jeng Y R, et al. Development of a straightness measuring system and compensation technique using multiple corner cubes for precision stages[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2010, 224(3):483-492.

[6] 贾立德, 郑子文, 李圣怡,等. 使用短基准的超精密长导轨直线度误差测量方法[J]. 机械工程学报, 2008, 44(9):141-147.

[7] 郭敬滨,李斌.大跨距、小步距法测量导轨系统的导轨直线度研究[J].机械科学与技术,2013,32(11): 1060-1063.

[8] 张刚强,陈建元,罗松保等.基于光电自准直仪的静压长导轨设计及测量[J].航空精密制造技术,2012, 48(2):6-8.

[9] 朱嘉,李醒飞,谭文斌.基于激光干涉仪的测量机几何误差检定技术[J].机械工程学报,2010,46(10): 25-30.

[10] 刘福文,马定,李天骄.直线导轨测量平台的设计与制造[J].精密制造与自动化,2015(2):26-29.

[11] 王孝坤.利用激光跟踪仪测量超长导轨直线度的方法[J].应用光学,2013,34(4):686-689.

[12] 房传明,陈长军.基于光学扫描法的导轨直线度测量方法[J].光学仪器,2015,37(2):95-99.

(编辑 李秀敏)

A Method for Measuring Straightness of Long Guideway Based on Stitching and Reconstruction

QIAN Lin-hong， LV Lei， XIA Huan

(Institute of Machinery Manufacturing Technology, China Academy of Engineering Physics, Mianyang Sichuan 621900,China)

In order to overcome the difficulty of the measurement of the full stroke straightness of the ultra-precision equipment long guide, a new method of stitching and reconstruction was proposed in this paper. First, profile of short reference was measured, which was used to compensate the measurement results of guideway. Second, effect of different tilt errors eliminating method was compared, and the appropriate method which could be applied to eliminate the tilt errors was confirmed. Besides，the effects of overlap length and frequency of stitching and reconstruction，environment noise on the measurement results were simulated. Finally, the straightness of ultra-precision aerostatic guide of diamond fly-cutting machine was measured. The measurement results show that the measurement error of the two methods was 15.8%, which verified the accuracy and validity of the measurement method proposed in this paper. It provides a new way to solve the measurement of the full stroke straightness of the ultra-precision equipment long guide.

ultra-precision;long guide;stitching;straightness;error

1001-2265(2017)05-0077-04

10.13462/j.cnki.mmtamt.2017.05.020

2016-11-30；

2017-01-24

武器装备技术基础项目资助(2016JS2.1)；中国工程物理研究院909重大科技专项资助(9120602)

钱林弘(1990—)，女，四川岳池县人，中国工程物理研究院机械制造工艺研究所助理工程师，硕士，研究方向为算法及数据处理，(E-mail)794673236@qq.com。

TH162；TG506

A