基于压电陶瓷的柔性机械臂主动振动控制实验研究*

陈 希,王 海*,陶 伟,薛 彬,杨春来

(1.安徽工程大学机械与汽车工程学院,安徽 芜湖 241000;2.先进数控与伺服驱动安徽省重点实验室,安徽 芜湖 241000)



基于压电陶瓷的柔性机械臂主动振动控制实验研究*

陈 希1,2,王 海1,2*,陶 伟1,2,薛 彬1,2,杨春来1,2

(1.安徽工程大学机械与汽车工程学院,安徽 芜湖 241000;2.先进数控与伺服驱动安徽省重点实验室,安徽 芜湖 241000)

柔性机构因其工作效率高,能量消耗低和结构简单等优点被广泛应用于机器人领域。但柔性机构由于刚度较低,易产生弹性振动,使机器人的定位精度和运动精度降低。为了验证在前期的工作中提出的柔性机械臂主动振动最优控制位置分析的正确性,搭建了一个基于Labview的测试系统。在柔性臂上不同位置粘贴压电片来实现对柔性臂不同位置的主动振动控制,通过测试系统得到最优控制位置处和最优控制位置附近的柔性机械臂振动的传感电压,根据控制前后传感电压的变化分析柔性臂抑制的强弱。根据实验结果显示,柔性臂在前三阶振动下,分别在其最优控制位置上获得最高的抑振率,从而验证了最优控制位置的有效性。

柔性机械臂;压电片;主动振动控制;最优控制位置;抑振率

机械臂通常分为刚性机械臂与柔性机械臂[1]。刚性机械臂因臂杆刚度高,关节变形小,在理论建模时通常被看做无变形的刚体,但刚性机械臂重量大,载荷质量比较低,难以满足高速重载的应用场合。而采用柔性结构的柔性机械臂因臂杆重量轻,具备运动速度快,能耗低、载荷质量比大等优点[2-3]。但因柔性臂杆固有的低刚度特性,易导致臂杆在运动过程中产生较大的弹性变形。因此,必须对柔性机械臂的弹性振动加以必要的控制,才能有效提高柔性机械臂的运动精度。

柔性机构的抑振控制可分为主动抑振控制和被动抑振控制。被动抑振控制为开环控制,稳定性高、控制器简单方便,但控制参数无法实施调整,只能适用于窄带振动抑制。Francisco[4]设计的基于被动阻尼的振动抑制方法,仅可抑制高频振动,对低频振动作用效果不大。

被动抑振控制的缺陷促进了主动抑振控制的发展[5]。目前,基于智能材料的传感器与驱动器用于柔性机械臂抑振控制的研究得到了较快的发展,这些传感器与驱动器具有结构简单,体积小,轻质,压电转换效率高等优点[6]。近年来的研究大多使用固定数量及位置的PZT片构建闭环控制系统实现抑振[7-9]。然而,柔性机构的振动在实际工况下通常是多种模态的耦合,因此采用可调整控制策略具有明显的控制效果[10-11]。

在本实验中,通过激振台使柔性臂受迫振动,并使用PZT片分别粘贴在柔性臂表面的不同位置,通过PZT片获得驱动电压来实现柔性臂不同位置的主动控制。通过基于Labview的测试系统,实现传感电压的测量。根据控制前后所获传感电压幅值的比较以分析控制器对柔性臂的控制效率。

1 基于压电陶瓷的柔性机械臂系统

以单自由度柔性机械臂为例,研究基于压电材料的柔性机械臂主动振动控制,根据Euler-Bernoulli理论,可将单自由度的柔性机械臂当作一个悬臂梁进行建模,如图1所示,PZT驱动器与传感器分别粘贴在柔性臂的上下表面,在图1中,横截面为矩形的悬臂梁在x=0处为固定端,在x=L处为自由端。Xai为第i片驱动器的初始位置,传感器与驱动器相对应地粘贴在柔性臂的另一侧;PZT1和传感器1作为一阶振动控制的驱动器和传感器;PZT2和传感器2作为二阶振动控制的驱动器和传感器;PZT3、PZT4和传感器3作为三阶振动控制的驱动器和传感器。L为悬臂梁的长度;l为压电片的长度。

图1 粘贴PZT传感器与驱动器的悬臂梁模型

柔性机械臂的动力学方程为:

(1)

式中:R(x)为广义位置函数,ρb为质量密度,Ab为梁的横截面积,Eb为杨氏模量,Ib为梁的转动惯量。用无穷级数来表示横向位移ω(x,t):

(2)

式中:ηi(t)为第i阶广义位移的时间函数,φi(t)为悬臂梁的第i阶模态振型。

在我们前期的工作中[12]已经得出柔性臂前三阶的谐振频率分别为15Hz,100Hz,250Hz。在COMSOL中构建悬臂梁与PZT驱动器的模型,其参数如表1所示。

表1 柔性臂与压电材料的参数

通过数值仿真获得悬臂梁的前三阶振型[12],其固有频率分别为15 Hz,100 Hz,250 Hz。如图2所示,悬臂梁一阶振动时的根部应变最大;二阶振动时悬臂梁的中间部分有最大变形;三阶振动时柔性臂两处应变最大。

图2 悬臂梁前三阶振型图

根据图2所示的前三阶振型可知,在一阶模态下,柔性臂振动时根部弯曲变形最大,将PZT1驱动器粘贴在柔性臂变形最大的位置,位于Xa1=0 mm处,传感器1与PZT1对称粘贴,此处为一阶振动的最优控制位置;柔性臂在二阶模态下的应变最大处在其中间长度位置,将PZT2驱动器粘贴在变形最大的位置,即Xa2=160 mm处,传感器2与PZT2对称粘贴,此处为二阶振动的最优控制位置;柔性臂在三阶振动时两处位置产生最大弯曲变形,两个PZT驱动器分别粘贴在Xa3=80 mm处与Xa4=230 mm处,传感器3与PZT3对称粘贴,由于两个PZT驱动器同时粘贴在两个最大弯曲变形处,因此这两个位置为三阶振动的最优控制位置。

2 基于压电陶瓷的柔性臂抑振测试系统

为了验证基于压电陶瓷控制器的主动振动控制策略的有效性,以及对柔性臂在前三阶振动时最优控制位置分析的正确性,使用如图3、图4所示的柔性臂抑振测试平台,采用基于压电陶瓷的振动控制方法进行实验,对其进行验证。实验设备如表2所示。

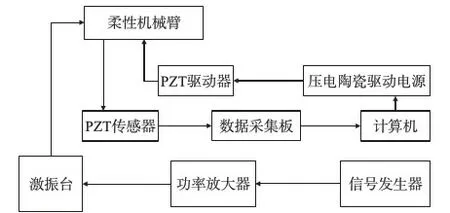
图3 柔性机械臂振动控制实验系统图

图4 柔性机械臂振动控制实验设备图

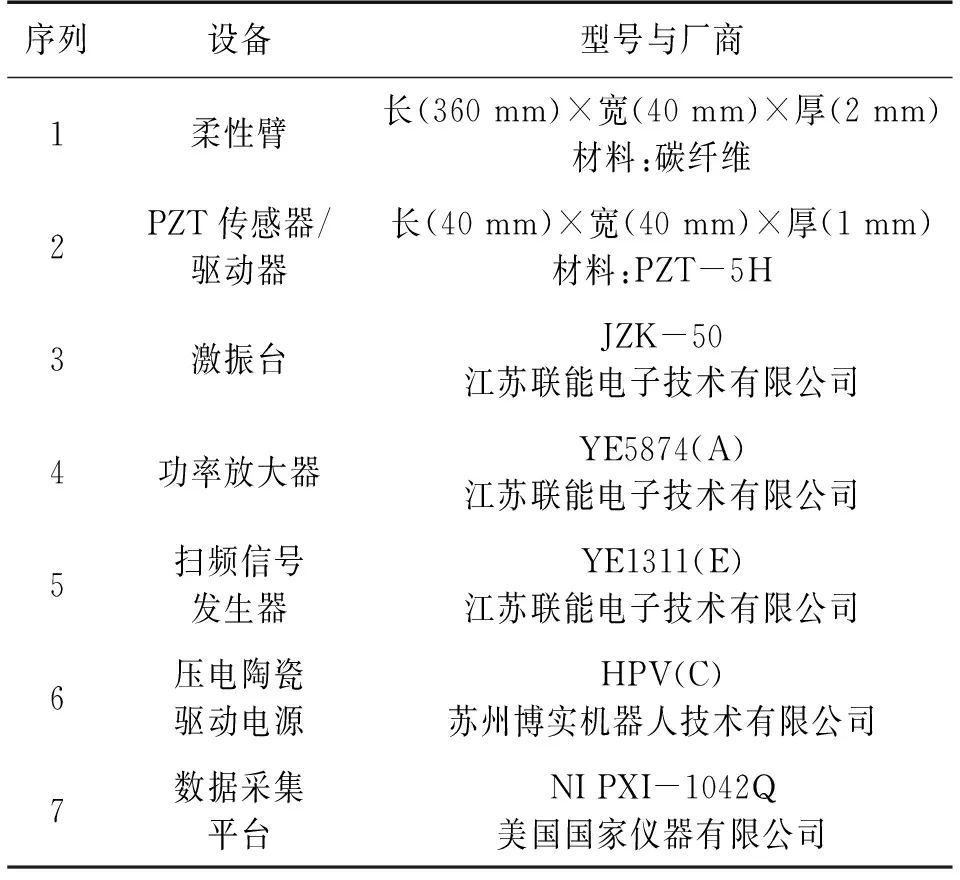
序列设备型号与厂商1柔性臂长(360mm)×宽(40mm)×厚(2mm)材料:碳纤维2PZT传感器/驱动器长(40mm)×宽(40mm)×厚(1mm)材料:PZT-5H3激振台JZK-50江苏联能电子技术有限公司4功率放大器YE5874(A)江苏联能电子技术有限公司5扫频信号发生器YE1311(E)江苏联能电子技术有限公司6压电陶瓷驱动电源HPV(C)苏州博实机器人技术有限公司7数据采集平台NIPXI-1042Q美国国家仪器有限公司

具体的系统控制过程如下:①信号发生器通过功率放大器驱动激振台带动柔性机械臂产生正弦振动;②PZT传感器将振动信号经过数据采集板传递到计算机,在计算机上显示柔性臂振动的传感电压;③计算机输出正弦电压信号通过压电陶瓷驱动电源驱动粘贴在柔性臂表面的PZT驱动器,PZT驱动器产生弯矩抑制柔性臂的振动;④柔性臂被抑振后的传感电压通过PZT传感器传递到计算机上。

对比柔性臂抑振前后传感电压的变化得出柔性臂抑振测试的效果。

在实验中,调节信号发生器和功率放大器使激振器产生幅值为1 mm,频率分别为15 Hz、100 Hz和250 Hz的正弦位移,激振器带动柔性臂分别在前三阶模态下振动。当PZT驱动器工作时,驱动信号设定为幅值为10 V,频率分别为15 Hz、 100 Hz和250 Hz的正弦电压。

对于柔性机械臂前三阶振动控制实验,具体实验步骤如下:①在一阶、二阶模态下,首先测得PZT驱动器不工作时的开环传感电压,然后测得在理论最优控制位置处粘贴PZT驱动器后柔性机械臂的振动的传感电压,最后PZT传感器位置不变,在最优控制位置附近移动PZT驱动器测得不同位置的传感电压;②在三阶模态下,首先测得两个PZT驱动器都不工作时的开环传感电压,然后测得在两个理论最优控制位置处同时粘贴PZT驱动器后柔性臂振动的传感电压,最后PZT传感器位置不变,PZT4位置不变,在距柔性臂夹紧端80 mm处附近移动PZT3得到不同位置的传感电压;同样PZT3位置不变,在距柔性臂夹紧端230 mm处附近移动PZT4得到不同位置的传感电压。

3 实验结果与分析

在每一阶模态下的最优控制位置处给PZT驱动器施加电压,在施加电压前后PZT传感器得到的数据如图5所示。

在最优控制位置处及其附近分别粘贴PZT驱动器,产生的弯矩控制柔性臂的每一阶振动,根据系统抑振前后传感电压变化曲线图判断其抑振效率。

定义抑振效率为:

(3)

式中:N为峰值数,pij为第j阶振动下的第i个峰值,pio为开环响应的第i个峰值。

如式(3)所示可得在各阶最优位置控制处PZT驱动器的抑振率。图5显示了前三阶在最优位置控制处受PZT驱动器抑振时的传感电压相比于开环响应分别获得了44.51%、45.66%和49.05%的抑制。

图5 柔性臂在前三阶谐振下的传感电压

在一阶、二阶模态下,在柔性机械臂上的不同位置分别粘贴PZT驱动器,测得不同位置的传感电压得到PZT驱动器对柔性机械臂的抑振率如图6、图7所示。在三阶模态下,由于柔性臂变形最大的位置有两个,在230mm处粘贴的PZT4位置不变,在第1个变形最大位置的附近(0～185mm范围内)分别移动PZT3,得到PZT3粘贴不同位置对柔性臂的抑振率如图8(a)所示;在80mm处粘贴的PZT3位置不变,在第2个变形最大位置的附近(120mm～320mm范围内)分别移动PZT4,得到PZT4粘贴不同位置对柔性臂的抑振率如图8(b)所示。

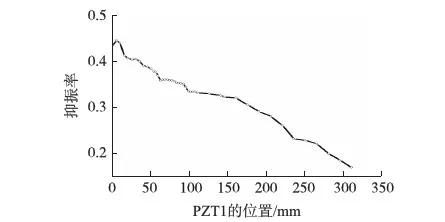
图6 不同位置PZT1驱动器对柔性臂的一阶抑振率

在图6中,从柔性臂夹紧端到距离夹紧端5mm处,PZT1驱动器对柔性臂的振动抑振率逐渐增加,从距离柔性臂夹紧端5mm到柔性臂末端,PZT1驱动器对柔性臂的振动抑振率逐渐减小,在5mm处振动抑制率最大为44.82%。

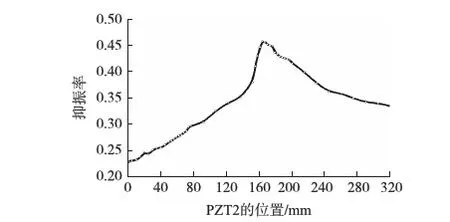
图7 不同位置PZT2驱动器对柔性臂的二阶抑振率

在图7中,二阶模态下从柔性臂夹紧端到距离夹紧端164mm处,PZT2驱动器对柔性臂的振动抑振率逐渐增加,从距离柔性臂夹紧端164mm到柔性臂末端,PZT2驱动器对柔性臂的振动抑振率逐渐减小,在164mm处振动抑制率最大为45.73%。

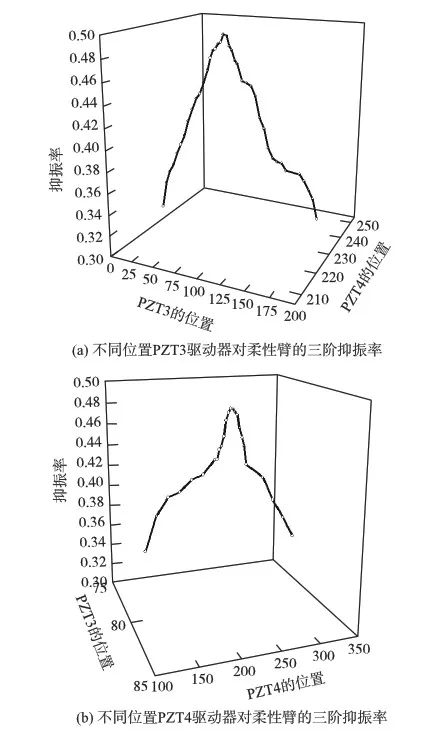
图8 不同位置PZT3和PZT4驱动器对柔性臂的三阶抑振率

在图8(a)中,PZT4驱动器在230mm处位置不变,PZT3驱动器在0至185mm处移动,两个驱动器同时对柔性臂振动控制的抑制率先增大后减小,当PZT3驱动器在78mm处,同时PZT4驱动器在230mm处对柔性臂的振动抑制率最大为49.31%;在图8(b)中,PZT3驱动器在80mm处位置不变,PZT4驱动器在120mm至320mm处移动,两个驱动器同时对柔性臂振动控制的抑制率先增大后减小,当PZT3驱动器在80mm处位置不变,同时PZT4驱动器在231mm处对柔性臂的振动抑制率最大为48.3%。据此可知,当柔性机械臂在一阶谐振频率下振动时,主动控制的最优位置靠近机械臂的夹紧端(x=5mm)。当柔性机械臂在二阶谐振频率下振动时,主动控制的最优控制位置为机械臂长度的中间位置(x=164mm)。当柔性机械臂在三阶谐振频率下振动时,两组实验分别是PZT4驱动器在230mm处、PZT3驱动器在78mm处同时抑振以及PZT3驱动器在80mm处、PZT4驱动器在231mm处同时抑振,三阶振动的柔性臂有最优的振动抑制。

将理论分析与实验结果所得到的最优控制位置相比较,如表3所示。

表3 不同模态下理论与实验得到的最优控制位置

由表3可知,在前三阶模态下,实验结果与仿真结果接近,验证了前期工作中提出的最优控制位置分析的正确性。

4 总结

为了验证柔性机械臂主动振动最优控制位置理论分析的正确性,通过基于压电陶瓷的柔性机械臂抑振测试系统得到不同模态下最优控制位置和最优控制位置附近的振动抑制率,经过分析得出最优控制位置并与理论仿真相比较,实验结果验证了理论分析的有效性。基于此,可得如下结论:在一阶谐振下,柔性臂的振动最优控制位置靠近柔性臂的夹紧端;柔性臂在二阶振动时,最优控制位置为机械臂的中间位置;柔性臂在三阶谐振时,距柔性臂根部80 mm,230 mm处为最优控制位置。另外在实验研究中,由于控制问题的复杂性。仍有许多问题需要进一步的研究:①柔性机械臂在同一位置处粘贴不同尺寸的PZT驱动器,得到的抑振效果不同,如何选出抑振率最优的PZT驱动器尺寸是后期的工作重点。②目前研究柔性臂的运动方向为横向,而机械臂的运动多为定轴转动。因此在改进的实验系统中可以使用步进电机连接柔性臂转动,以替代激振器的位移驱动。

[1] Khairudin M,Mohamed Z,Zain Z M. Modeling of a Two-Link Flexible Manipulator[J]. Instrumentation and Mechatronic Engineering,2009,35(17):191-199.

[2] 崔博文,陈剑,陈心昭. 刚性臂机器人自适应控制方法研究进展[J]. 机电工程,2005,22(12):56-60.

[3] 宋轶民,余跃庆,张策,等. 柔性机器人动力学分析与振动控制研究综述[J]. 机械设计,2003,20(4):1-5.

[4] Francisco Palacios-Qui,Hamid R Karimi,Josep Rubio-Massegu. Passive-Damping Design for Vibration Control of Large Structures[J]. 10th IEEE International Conference on Control and Automation,2013,60:33-38.

[5] Djojodihardjo H,Jafari M,Wiriadidjaja S. Active Vibration Suppression of an Elastic Piezoelectric Sensor and Actuator Fitted Cantilevered Beam Configurations as a Generic Smart Composite Structure[J]. Composite Structures,2015,158(2/3):848-863.

[6] Chacon J,Beschiy M,Sanchez J,et al. Experimental Analysis of a Remote Event-Based PID Controller in a Flexible Link System[J]. IEEE Emerging Technology and Factory Automation,2014,4(8):1-6.

[7] Crawley E F,DeLuis J. Use of Piezoelectric Actuators as Elements of Intelligent Structures[J]. AIAA Journal,1987,89(2/3):1373-1385.

[8] 朱灯林,吕蕊,俞洁. 压电智能悬臂梁的压电片位置尺寸及控制融合优化设计[J]. 机械工程,2009,45(2):262-267.

[9] 曹玉岩,王志臣,付世欣,等. 智能桁架结构最优振动控制与作动器优化配置[J]. 振动与冲击,2015,23(5):26-32.

[10] 谭国金,刘寒冰,程永春,等. 基于车-桥耦合振动的简支梁桥冲击效应[J]. 吉林大学学报,2011,34(1):62-67.

[11] 张端,林晨宽,何熊熊. 低频振动能量收集装置的设计和数值模拟[J]. 传感技术学报,2012,25(9):1268-1273.

[12] 王海,薛彬,杨春来,等. 基于压电陶瓷的柔性机器人主动抑振控制策略研究[J]. 传感技术学报,2016,29(7):1016-1020.

Experimental Study of Active Vibration Control of Flexible Manipulator Based on Piezoelectric Ceramic Elements*

CHEN Xi1,2,WANG Hai1,2*,TAO Wei1,2,XUE Bin1,2,YANG Chunlai1,2

(1.College of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu Anhui 241000,China; 2.An Hui Key Laboratory of Advanced Numerical Control and Servo Technology,Wuhu Anhui 241000,China)

Due to high efficiency,low energy consumption and simple structure,flexible beams are widely used in robotics. Elastic vibration of flexible beams in robotics is easy to produce during operation,which owing to the nature low stiffness of the flexible structures. Elastic vibration of robotics will lead to poor positioning accuracy or low motion precision. The optimal control position of active vibration control of flexible manipulator was obtained by numerical simulation in the previous work. In order to verify the correctness of the optimal control position analysis of active vibration of flexible manipulator proposed in the previous work,a test system based on Labview is set up. The vibration control of the flexible manipulator at different positions is acquired by attaching the PZT patchs at different positions on the flexible arm. The sensor voltage of the flexible manipulator near the optimal control position and the optimal control position is obtained by the test system. The strength of the flexible arm suppression is analyzed by the sensors voltage before and after the control. According to the experimental results,the flexible arm achieves the highest vibration suppression rate at its optimal control position under the first three orders of vibration,and the effectiveness of optimal control position is verified.

flexible manipulator;piezoelectric patches;active vibration control;optimal control position;suppression rate

陈 希(1992-),男,安徽省淮北市人,安徽工程大学机械与汽车工程学院,硕士研究生,主要研究方向为智能机器人,1832544914@qq.com;

王 海(1976-),男,安徽省芜湖市人,安徽工程大学机械与汽车工程学院,博士,教授,主要研究方向为机器人控制技术,wanghai.20000@163.com。

项目来源:国家自然科学基金项目(51275001,51375469);安徽省自然科学基金项目(KJ2012A033)

2016-09-05 修改日期:2017-01-14

文献标识码:A 文章编号:1004-1699(2017)05-0777-05

C:7230

10.3969/j.issn.1004-1699.2017.05.024