基于遗传算法的wMTP系统布局优化研究*

张耀华,林嘉睿*,任 瑜,任永杰

(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072;2.上海市计量测试技术研究院,上海 200000)



基于遗传算法的wMTP系统布局优化研究*

张耀华1,林嘉睿1*,任 瑜2,任永杰1

(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072;2.上海市计量测试技术研究院,上海 200000)

室内空间测量定位系统(wMTP)是一种采用光平面交会的分布式大尺寸室内空间坐标测量系统。发射站的布局直接影响着该测量系统的测量误差、测量精度和其使用效能,而传统的L、C等测量模型在实际过程中受现场条件限制,测量精度比较低。为优化测量系统的网络布局,从该系统的空间多角度交会测量模型入手,以测量精度为优化目标,采用遗传算法作为优化工具,建立了以三维坐标数据对光平面扫描角的导数为关键的定位误差模型,以协方差来反映测量精度,更简单、直接地实现了在指定测量空间下的最优网络布局。最后设计了实验进行验证,实验结果表明该方法能有效优化布局,提高测量精度。

测量定位系统;交会测量;测量精度;布局优化

室内空间测量定位系统wMTP(workshop Measurement and Positioning System),是一类基于光电扫描原理的新型工业大尺寸坐标测量系统,具有测量范围广、测量精度高、扩展性好和并行实时测量等优点,在飞机机身对接定位、货轮建造等大型设备制造领域受到广泛应用[1]。该系统主要由分布在工作空间四周的激光发射站和位于各个待测点的接收器以及解算计算机组成,如图1所示。这种分布式的特点原理上可同时测量多个的待测接收器,真正实现多任务并行测量[2-3]。

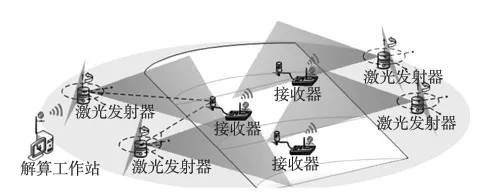
图1 测量系统组成图

由于接收器的可探测区域与接收器的接收角度限制,以及接收器内部光电二极管与球心的距离误差等因素影响,wMTP测量系统的不同发射站放置在空间不同位置,在同一个测点处产生的测量误差[4]会有显著差别。因此发射站的空间几何布局对整个系统的测量精度有着结构性的影响。如何给出一种方法来优化发射站的布局以提高wMTP系统的测量精度是重要而有意义的问题。

天津大学熊芝对室内空间测量定位系统的几种典型布局进行了分析,给出了误差分布特性[4]。但该方法在一定程度上还依赖于人工参与,可行性解的搜索也不够智能,难以直接应用于环境复杂的实际测量任务中,因此,需要一种自动化程度高,且能适应复杂测量环境的布局优化方法。Zheng Wang、Alistair Forbes 和Paul Maropoulos采用模式搜索法对距离交会测量中激光跟踪仪的站位进行优化,使测量精度显著提高[5-6]。模式搜索法具有编程简单,容易实现的优点,但是其收敛速度比较慢,适合变量较少的优化问题,而且需要合适的初值以保证收敛于全局最优值。Fiorenzo Franceschini 和 Maurizio Galetto等提出了基于网格和遗传算法的MScMS传感器网络模块化布局方法[7-8]。结果显示,与基于网格算法的方案相比,基于遗传算法的优化方案更好的适应了现实的测量环境,由于其考虑因素较多,对测量精度的改善不是很明显[9-11]。

本文从交会测量角度出发,研究了发射站激光平面在测量点处不同几何交会与测量稳定性之间的关系,通过分析整个测量系统的解算方程,推导建立了由三维数据对测量值的导数构成的协方差矩阵来评价布局优劣的数学模型,即方差越小,代表交会越稳定,测量精度也就越高,布局越优。本文以此数学模型为基础来搜寻固定测量空间下的最优布局,并采用遗传算法来搜索可行解,该算法很好的解决了wMTP系统测量范围广、搜索空间大、计算复杂等问题,且可得到比较好的测量精度。

1 wMTP测量原理与定位误差模型

1.1 wMTP测量原理

wMTP测量系统主要包括分布在工作空间四周的激光发射站和位于各个待测点的接收器,如图1所示。

激光发射站由旋转头及基座组成,基座内部装有红外脉冲激光器,旋转头内部装有两台一字线红外激光器。工作时,旋转头在电机驱动下绕轴匀速逆时针旋转,每当旋转头转至一个预定的初始位置时,会触发基座上的红外脉冲激光器发出同步光信号作为计时起点。当旋转光面扫过接收器或接收器接收到同步标记光信号时,接收器将产生扫描信号,计算机通过采集各接收器记录的时间值和发射站的转速可以计算出接收器的虚拟平面[12],类似的,得到至少3个同样的平面后,就可以解算出接收器的空间位置坐标Prx(x,y,z),测量交会示意图如图2所示。

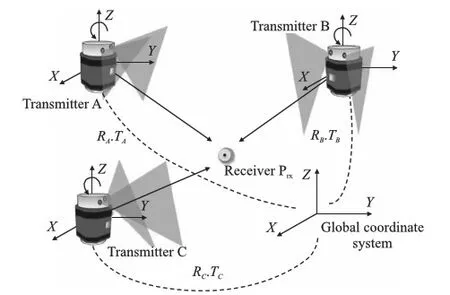
图2 多平面交汇示意图

每一个平面可以确定一个方程,利用多平面约束可得解算方程组[12]如下:

[aim,bim,cim]·Rim(θ)·[Rm·[xyz]T+Tm]+dim=0

(1)

式中:aim,bim,cim,dim表示第m个发射站的第i个初始激光平面方程的系数,i∈{1,2},m∈N+,Rim(θ)表示激光平面旋转θ的旋转矩阵,Rm、Tm分别表示全局测量坐标系到发射站坐标系的旋转矩阵和平移矩阵。

1.2 定位误差模型

把发射站按照不同激光平面的约束方程进行计算,用ψ2m-1(p,C)表示第m台发射站的第1个平面的约束方程,用ψ2m(p,C)表示第m台发射站的第2个平面的约束方程,则多平面约束方程组可以转变为如下测量模型:

(2)

利用最小二乘法使误差的平方和最小:

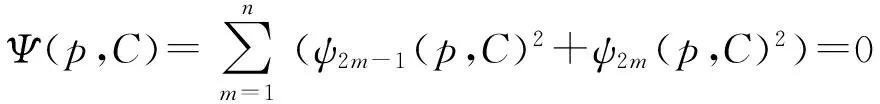
(3)

式中:n为发射站站数,n≥2;(ami,bmi,cmi,dmi)为第m台发射站的第i个激光平面的平面参数(m=1,2,…,n,i=1,2);测量值C=(θ11,θ12,θ21,θ22,…,θn1,θn2),θmk为第m台发射站的第i个激光平面到被测点的扫描角(m=1,2,…,n,i=1,2);Rm和Tm分别为全局坐标系到发射站坐标系的旋转矩阵和平移向量。

根据隐函数求导法则可得三维数据p对测量值C的导数dp/dC为:

(4)

式中:(∂Φ/∂p)-1为∂Φ/∂p的广义逆矩阵,∂Φ/∂p为函数Φ关于变量p的雅可比矩阵:

Φ=(∂Φ/∂p)T

(5)

根据方差-协方差传播律,三维数据的协方差矩阵可表示为:

(6)

(7)

式中:σi为第i台发射站的扫描角标准差,σp为空间测量误差,σx、σy、σz分别代表x、y、z方向的定位误差。定位误差越小,所测精度越高,说明系统布局越优。

2 优化算法设计

2.1 遗传算法

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法。其本质是一种高效、并行、全局搜索的方法[13]。遗传算法使用适者生存的原则,在潜在的解决方案种群中,逐次产生一个近似最优的方案[14]。它从代表问题可能潜在解集的一个种群开始,将解空间映射到编码空间,用二进制数表示一个解,称为染色体或个体,然后根据适应度大小来选择个体,并通过个体交叉和变异操作来产生新的更适应环境的一群个体,使群体进化到搜索空间中越来越好的区域,这样一代一代地不断繁衍进化,最后收敛到一群最适应环境的个体,求得问题的最优解[15]。

室内空间测量定位系统因为测量范围比较广泛、搜索解的空间比较大,计算量也较大,因此用遗传算法来优化布局会大幅度降低计算量与复杂度,进而快速找到该测量范围内的近似最优解。

2.2 具体算法设计

布站区域是一个三维的立体空间,在全局坐标系下每个发射站的坐标为P(xn,yn,zn),n为发射站个数,n个发射站的坐标就组成了解的空间。遗传算法首先要进行编码工作,即将发射站坐标转换成二进制串。根据实验室环境的布站区域确定xn、yn、zn的取值范围,设xn∈[X1,X2],搜索的步长为K,K就确定了搜索的精度。对xn进行二进制编码

(8)

式中:L为二进制编码的长度,X2-X1为搜索范围,K为搜索步长。对yn和zn采用同样的方式进行编码。每一种布局映射一个个体,然后按照适应度大小来选择个体。遗传算法采用适应度函数来确定各个个体进化到下一代群体中的机会多少,进而反映空间发射站布局的优劣。因此,式(7)可以作为算法的适应度函数Fi,代表每一种布局对应的测试交会点σp的值,即Fi=σp。适应概率可用式(9)计算

(9)

式中:P代表适应概率。每个个体都以P的概率遗传到下一代,当这一代种群中某个个体的Pi最小时,该个体将会被淘汰,同时保留这一代中的最优个体遗传到下一代,这样就可以提高收敛速度。并通过交叉、变异操作来产生新的个体,即系统中的新的发射站坐标。这样后代种群的适应度就会比上一代种群适应度高,通过算法的多次迭代以后,末代种群的最优个体解码就可以作为该测量范围内的近似最优解了。

图3 测量误差仿真结果图

3 实验结果与分析

3.1 仿真实验

为了验证本文提出的基于遗传算法的的测量精度模型布局优化方法,建立了仿真实验系统,对比优化前后在相同测量区域的所测量的误差精度。实验中,发射站内部参数为激光器光轴与水平面夹角off_angle=0,平面倾角dip=45°,d=0,扫描光平面扇角divergence=60°。

在仿真实验中,将测量区域设定为一个特定的平面区域,x∈[4 000,4 500]&[5 500,6 000],y∈[0,500]&[1 500,2 000],z=0,单位mm。优化前发射站的位置坐标为(0,0,0),(0,1 000,0),(0,2 000,0),(1000,-500,0),(1 000,2 500,0),测量误差如图3(a)所示,可以看到误差范围为0.11～,0.20,优化后的发射站的坐标为(0,1 000,0),(1 000,2 500,0),(1 000,-1 500,0),(3 000,3 500,0),(3 000,-1 500,0),优化后测量误差如图3(b)所示,误差为0.07～0.11,整体明显小于优化前的测量误差,提高了测量精度,说明我们所采用的基于遗传算法的优化模型是有效的。

3.2 实验验证

为了计算本文提出测量模型优化方法的测量误差,在实验室条件下,搭建如图4所示实验平台,在测量过程中,以激光跟踪仪坐标系作为全局坐标系,获取测量区域在该全局坐标系下的坐标范围,在此实验中,要求坐标测量误差的最大允许值为0.4 mm。

图4 五站测量系统测量示意图

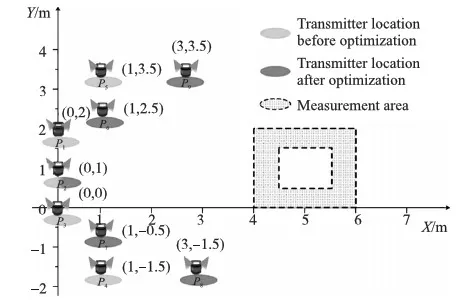
图5 优化前后发射站位置示意图

然后将测量区域设定为[1 m,1 m,2 m]的立体空间,在无遮挡,并且保证每个发射站的测量信号在布局范围内均可以保持畅通的情况下,根据实验室条件,划定布局区域,实验布局如图5所示。根据经验将发射站放置到没有遮挡,且交会角度接近于90°的位置作为优化前的位置坐标,由于接收器的机械结构与内部传感器的位置关系,接收器的接收角度限定于±70°,所以发射站不能放置在单个接收器四周,通过激光跟踪仪标定这3个发射站的外参,由此推算出发射站在全局坐标系下的坐标。

标定完毕后,在测量区域内随机选取10个待测点,每个待测点处放置一个接收器底座,并且保持布局优化前后底座位置不发生变化。为比对wMTP系统的测量精度,先用激光跟踪仪对测点进行测量,记录测点坐标,结果如表1所示。

然后用wMTP系统进行多次测量,分别记录测量数据,取平均值,结果如表2。接着利用本文提出的方法对布局进行优化,根据优化结果,将发射站移至优化位置,重新利用激光跟踪仪标定外参,同样对选取的10个点再次用wMTP系统进行多次测量,记录测量数据,取平均值,结果如表3。最后对优化前后得到的实验数据进行分析比较。

表1 激光跟踪仪测点数据

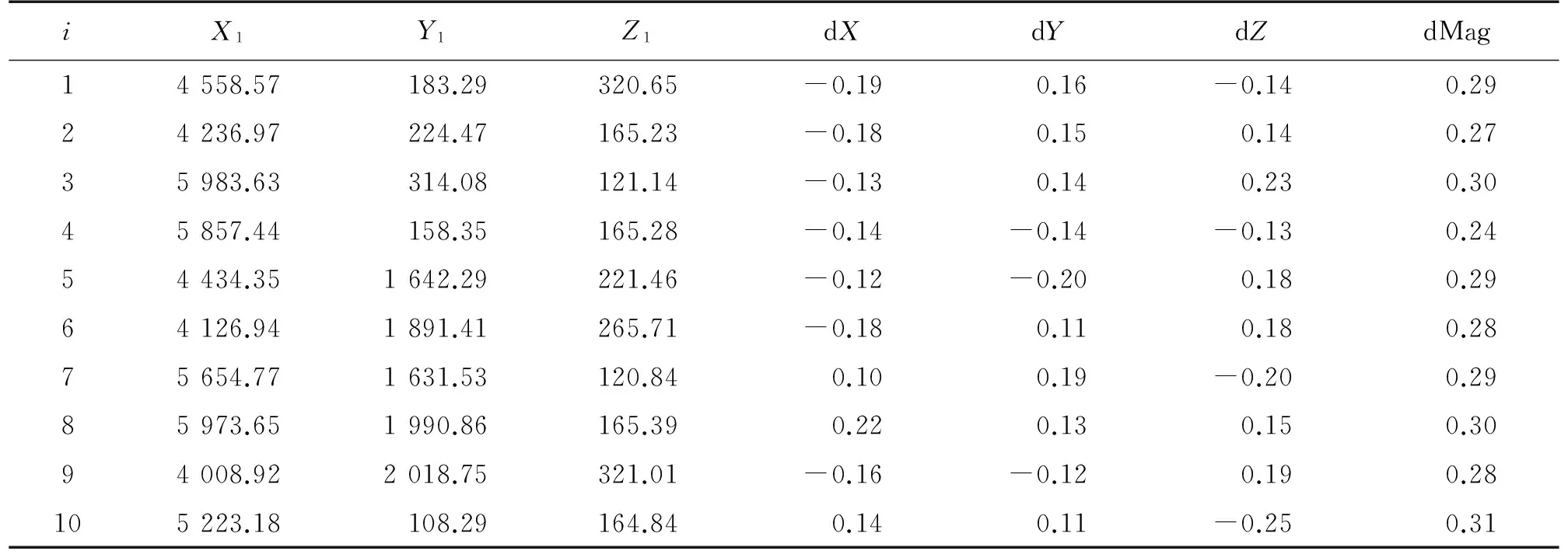
表2 wMTP优化前测点数据

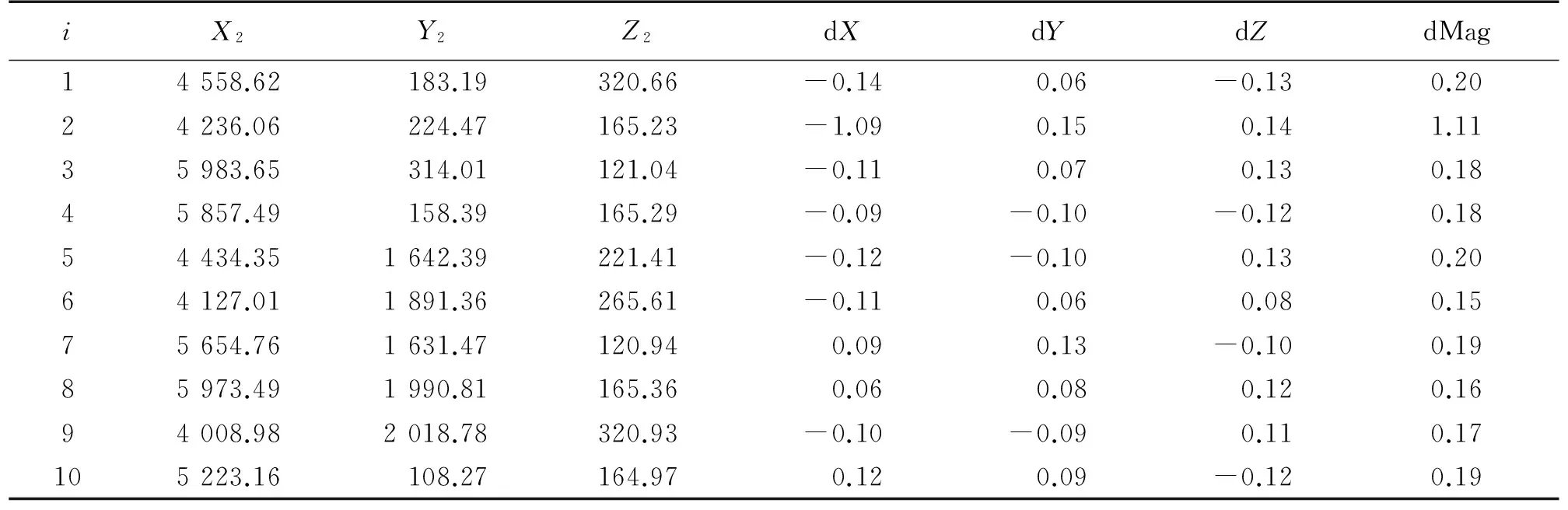
表3 wMTP优化后测点数据

表2、表3中,i表示测点编号,dx、dy、dz列分别表示wMTP测量数据与激光跟踪仪在x、y、z轴方向的误差,dMag列表示wMTP测量系统结果与激光跟踪仪测量结果的距离差,用来衡量wMTP的测量精度,即σp。利用优化前后的σp数据绘制图6。

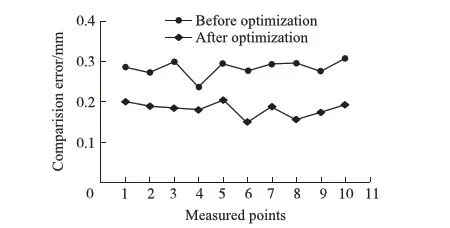
图6 优化前后测量误差对比图

由图6可以看出优化后的测量值标准差要整体小于优化前的标准差,并且由表2、表3可以看到在x轴,y轴,z轴3个方向误差均减小了,说明对于整个测量区域,优化后的空间误差更小,所测精度更高。

实验说明,本文建立的以三维坐标数据对光平面扫描角的导数为关键的定位误差模型针对不同类型的测量区域都可以减小测量误差,提高测量精度,具有很高的实用性,且利用协方差来评价测量精度更简单、直接。

4 结论

室内空间测量定位系统的不同布局对测量精度有很大的影响,本文通过分析已知空间位置的发射站的测量模型、求解三维坐标数据对光平面扫描角的导数,并根据方差-协方差传播律得到三维数据的协方差矩阵,进而得到测量误差,更直接,简洁的得出wMTP发射站激光平面在测量点处的测量结果,在给定区域内搜索较优布局,使测量误差尽可能小,以此作为优化目标,通过遗传算法来搜索可行解。

为验证方法的可行性,设计了五台发射站对特定测量区域进行优化的仿真实验,并且在实验室可行的条件下对仿真实验进行了系统搭建与验证,利用激光跟踪仪对测量点进行标定,然后对wMTP测量系统发射站进行布局,得出优化前后测量结果,与激光跟踪仪数据进行比对以验证优化效果。实验结果表明,利用遗传算法对本文提出的测量模型进行优化,针对性强,优化结果明显,能够有效提高空间测量精度,具有很高的实际应用价值。

[1] 熊芝,邾继贵,耿磊,等. 室内测量定位系统水平测角性能的检定[J]. 光电子·激光,2012,23(2):291-296.

[2] 杨凌辉,杨学友,邾继贵,等. 基于光电扫描的工作空间测量定位系统误差分析[J]. 光电子·激光,2010,21(12):1829-1833.

[3] 王琼,邾继贵,薛彬,等. wMTP系统中扫描光面的拟合与评定技术[J]. 光电工程,2013,40(6):94-102.

[4] 熊芝. wMTP空间测量定位网络布局优化研究[D]. 天津:天津大学,2012:19-57.

[5] Maurizio G,Barbara P. Optimal Sensor Positioning for Large Scale Metrology Applications[J]. Precision Engineering,2010(34):563-567.

[6] Muelaner J E,Wang Z,Jamshidi J,et al. Study of the Uncertainty of Angle Measurement for a Rotary-Laser Automatic Theodolite(R-LAT)[J]. Proceedings of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture,2008,223(B3):217-229.

[7] Fiorenzo F,Maurizio G. The Problem of Distributed Wireless Sensor Positioning in the Mobile Spatial Coordinate Measuring System(MSCMS)[C/CD]//Proceedings of the 9th Biennial ASME Conference on Engineering Systems Design and Analysis ESDA08,Haifa,Israel,2008,July 7-9.

[8] Maisano D A,Jamshidi J,Franceschini F,et al. Indoor GTP:System Functionality and Initial Performance Evaluation[J]. International Journal of Manufacturing Research,2008,3(3):335-343.

[9] Maisano D A,Jamshidi J,Franceschini F,et al. Indoor GTP:System Functionlity and Initial Performance Aluation[J]. International Journalof Manufacturing Research,2008,3(3):35-343.

[10] Fiorenzo Franceschini,Maurizio Galetto,Domenico Maisanoa,et al. Online Diagnostics in the Mobile Spatial Coordinate Measuring Syste(MScMS)[J]. Precision Engineering,2009,33(4):408-417.

[11] Carlo F,Luca M,Julian F,et al. Sources of Variability in the Set-Up of an Indoor GTP[J]. International Journal of Computer Integrated Manufacturing,2010,23(6):487-499.

[12] 端木琼,杨学友,邾继贵,等. 基于光电扫描的三维坐标测量系统[J]. 红外与激光工程,2011,40(10):2014-2019.

[13] 马永杰,云文霞. 遗传算法研究进展[J]. 计算机应用研究,2012(4):1201-1206.

[14] Triggs B,Mclauchlan P F,Hartley R I,et al. Bundle Adjustment—A Modern Synthesis[C]//Proceedings of the International Workshop on Vision Algorithms:Theory and Practice,1999:298-372.

[15] 谢鹏,张红梅. 基于自适应遗传算法的EHA控制器优化设计[J]. 传感技术学报,2016,29(6):909-914.

Placement Optimization for Workshop Measurement and Positioning System Based on Genetic Algorithm*

ZHANG Yaohua1,LIN Jiarui1*,REN Yu2,REN Yongjie1

(1.State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China;2.Shanghai Institute of Metrology and Testing Technology,Shanghai 200000,China)

Workshop Measurement and Positioning System is a type of distributed large-scale indoor measurement system based on the intersection of optical planes. Among the multiple factors affecting measurement errors,the deployment of transmitter is regarded as a direct one influencing the system measuring accuracy and utility efficiency,however,the traditional evaluation models like L,C etc are practically used with lower precision restricted by field conditions. To optimize the measurement system network placement,these researches start with the spatial multi-angle intersection model of this system,take the measuring accuracy as optimization aim,and use genetic algorithm as optimization toolbox,then establish a positioning error model with key values of derivative that 3D data to scanning angle of light plane,characterize the precision with the covariance,more easily and directly produce the optimum network layout of the appointed workspace. Finally,the designed experimental validation shows that this method is effective to optimize the deployment and enhance the precision of measurement.

measurement positioning system;intersection measurement;accuracy of measurement;layout optimization

张耀华(1990-),女,天津大学精密仪器与光电子工程学院硕士研究生,主要研究方向为光电检测、大尺寸测量技术研究;

林嘉睿(1984-),男,福建泉州人,博士,硕士生导师,主要从事激光及光电检测、大尺寸测量技术研究。

项目来源:国家自然科学基金项目(51305297,51475329);国家重大科学仪器设备开发专项子任务项目(2013YQ35074702);天津市应用基础与前沿技术研究计划项目(15JCQNJC04600)

2016-08-30 修改日期:2016-12-20

TN247

A

1004-1699(2017)05-0746-06

C:7230

10.3969/j.issn.1004-1699.2017.05.019