水火发电系统随机生产模拟的两阶段定区间等效电量函数法

胡晓飞 ，林 洁 ，郭瑞鹏 ，汤 伟 ，杨 铖 ，刘俊宏

（1.国网安徽省电力公司电力调度控制中心，安徽 合肥 230022；2.广西电网公司电力调度控制中心，广西 南宁 530023；3.浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

电力系统随机生产模拟是指通过优化发电机组的生产情况，考虑机组的随机故障及电力负荷的随机性，从而计算出最优运行方式下各机组的发电量、系统的生产成本及系统的可靠性指标［1-4］。目前国内外专家学者已经提出了多种随机生产模拟算法，广泛应用在电力系统电源规划、运行规划以及可靠性评估等方面。文献［5］用随机分布的半不变量这一数字特征来描述系统的持续负荷曲线和机组的随机停运，进而提出了半不变量法。文献［6］提出的等效电量函数法是直接利用电量函数进行卷积运算，其计算量较小，且精度较高，适用于有多座水电厂的电力系统的随机生产模拟。文献［7］在随机生产模拟中考虑网络的影响，采用组合电力系统等效负荷持续曲线法实现发输电系统的可靠性评估。

电力系统随机生产模拟的主要内容是按各发电机组的经济优先顺序安排其运行，确定机组的最优带负荷位置，以降低系统总的生产成本。对于含有水电机组或抽水蓄能机组的系统而言，应充分利用水力资源。通常认为火电机组的发电量只受机组容量的约束，不受一次能源的约束；而水电机组的发电量受到一次能源的约束，由水文情况及水库调度决定。在随机生产模拟中，火电机组按照机组容量运行，水电机组则按照计划电量运行。当电力系统中只有火电机组时，可以按照经济指标确定带负荷顺序，整个随机生产模拟过程比较简单［8］；但是当系统中存在水电机组时，不能事先确定带负荷顺序。文献［9-10］将水电从时序负荷曲线中分离得到净时序负荷曲线，然后对净时序负荷曲线进行随机生产模拟，这种确定性方法虽然简单易行，但是因为没有优化水电机组的运行位置，故无法充分利用水电的经济性。文献［11］将系统中所有水电机组等效成一台机组进行处理，但对水电比重较大的电力系统而言显得过分粗略。文献［12］讨论了对水电机组进行随机生产模拟的原理，给出了水电机组带负荷位置的准则，并提出了将多台水电机组合并为一台等效机组的方法，以处理水电机组运行位置重叠的情况。该方法避免了反复利用卷积及反卷积运算的试探过程，简化了程序，大幅提高了计算效率，并得到了推广应用。

本文分析了等效电量函数有效区间的变化特征，通过对卷积运算进行平移变换，得到了固定的有效区间，提出了定区间等效电量函数法，进而在误差来源分析的基础上提出了用于水火发电系统随机生产模拟的两阶段定区间等效电量函数法：第一阶段协调优化水火电机组带负荷位置，第二阶段模拟存在空闲容量的水电厂。通过对IEEE-RTS 79修正及扩大系统的仿真分析验证了所提方法的准确性和高效性。

1 等效电量函数法及其改进

1.1 等效电量函数法简介

等效电量函数法的关键是将持续负荷曲线沿横轴等间隔分段，积分得到各段的对应电量，从而将卷积运算转换成加法运算［13］，如式（1）、（2）所示。

其中，f（0）（x）为原始等效持续负荷曲线；Δx 为间隔宽度；J为整数，表示间隔编号；E（i）（J）为前 i台机组安排运行后第J个间隔的等效电量函数；pi、qi分别为发电机组 i的可用率、故障率，且 qi=1-pi；Ki=Ci／Δx，Ci为发电机组i的容量，实际应用中应取足够小的Δx，使得所有的Ki均为整数。各机组容量的“最大公因子”是保证 Ki均为整数的最大间隔［14］。

机组i的发电量为：

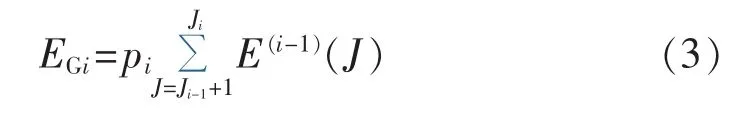
其中

若系统的机组数量为n，则系统可靠性指标失负荷概率 LOLP（Loss Of Load Probability）、失负荷电量期望值 EENS（Expected Energy Not Supplied）和失负荷功率期望值EDNS（Expected Demand Not Supplied）分别为：

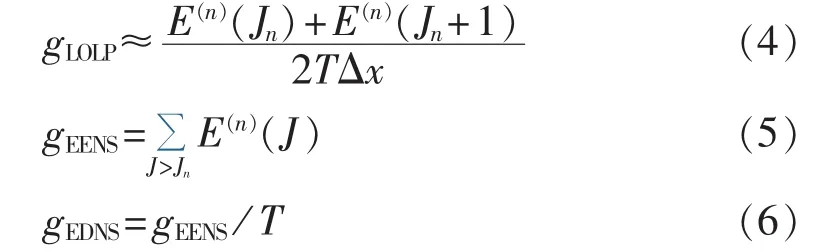
其中，T为随机生产模拟的周期。

1.2 定区间等效电量函数法

若系统的最大负荷为xmax，则由式（1）可以看出，E（0）（J）≠0 所对应的 J 的区间为［0，［xmax／Δx］］（［·］表示大于等于相应值的最小整数），称之为有效区间，区间宽度为［xmax／Δx］。

由式（2）得，E（i）（J）的有效区间为［0，［xmax／Δx］+Ji］。 随着模拟机组的增加，E（i）（J）有效区间的宽度随之增大，这不仅增加了算法的内存空间，也使得内存分配策略复杂化。

由式（3）可以看出，对每台发电机组的卷积运算应从下一台发电机组带负荷的位置算起。因为已经得到本台机组和之前机组的发电量，故其并不受本台机组停运的影响［15］。即对机组i进行模拟时，可以不关心区间［0，Ji-1）的 E（i-1）（J）值；当机组 i模拟完成后，就可以不关心区间［0，Ji）的 E（i）（J）值，所需关注的区间仅为［Ji，［xmax／Δx］+Ji］，其区间宽度也是［xmax／Δx］。由此可见，随机生产模拟所需关注的区间宽度是不变的，但所关注的区间位置在模拟过程不断右移。为了得到固定不变的关注区间，可以考虑对E（i）（J）进行左移变换。

将函数 E（i）（J）左移 Ji得到新的等效电量函数为：

显然，当i=0时，有：

将式（2）代入式（7），则有：

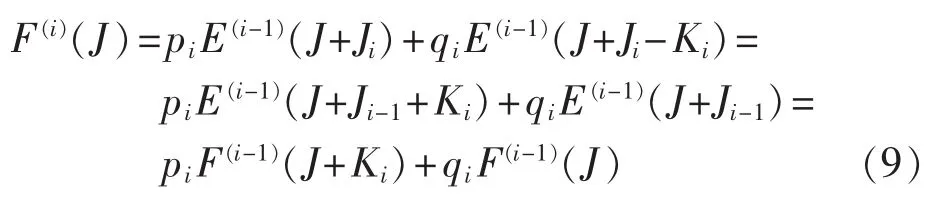
由式（3）和（7）可得，机组 i的发电量为：

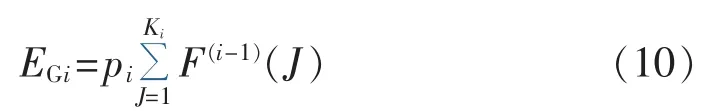
根据式（8）—（10）进行随机生产模拟，F（i）（J）需要计算的区间恒为［1，［xmax／Δx］］，这样可简化内存分配策略，减少所需的内存空间，使得算法的实现更为简洁高效。

将式（7）代入式（4）和（5）可得定区间等效电量函数法的LOLP和EENS计算公式为：

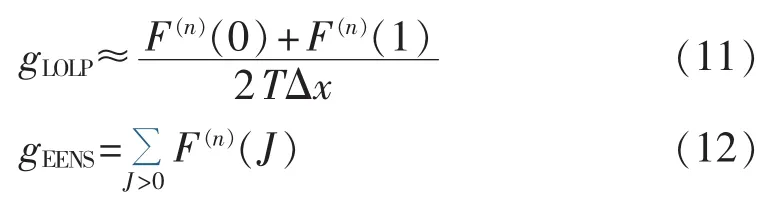
2 两阶段定区间等效电量函数法

2.1 水火发电系统随机生产模拟

文献［12］详细介绍了多台水电机组的随机生产模拟方法。考虑到实际生产中一般是给定整座水电厂的电量计划，故可以将多机随机生产模拟方法推广应用到多座水电厂。对水电厂进行全容量分配，对应于对各水电机组逐一进行全容量分配；对水电厂按给定电量分配则需对其水电机组逐一进行模拟，若机组全容量分配仍未达到给定电量，则需对下一台机组进行分配，否则需要根据电厂电量减去已模拟机组电量，对当前机组进行定电量分配。

随机生产模拟需要确定机组的带负荷顺序，在充分利用水能的同时使得效率高的机组多发电。火电机组一般按照其平均煤耗由小到大确定相对带负荷顺序［16］；文献［17］根据负荷利用小时数由大到小确定水电机组的相对带负荷顺序。为了考虑水电机组强迫停运的影响，本文根据式（13）定义的有效容量负载率由大到小确定各水电厂的相对带负荷顺序。

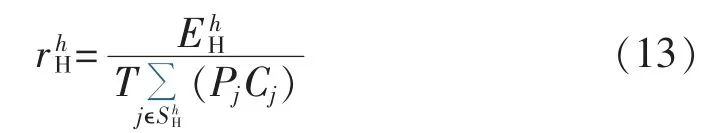
其中和分别为水电厂h的有效容量负载率、计划电量和水电机组集合；等式右端的分母为水电厂在所有机组均全容量运行时的可发电量期望值。

对于定电量计划的水电厂，其最优运行条件是各机组的容量和电厂电量都能得到充分利用。理论上可能存在以下3种情况：给定电量极充足，即使承担基荷仍无法完成计划电量，即需要弃水，一般对应于丰水期的情况，在模拟中应优先带负荷；给定电量适中，需与火电机组相协调以确定经济带负荷位置；给定电量极匮乏，即使最后带负荷仍无法充分利用所有机组的容量，一般对应于枯水期的情况。对于前2种情况，水电厂各机组的容量均可以得到充分利用；对于第3种情况，水电厂将存在空闲容量，即部分机组存在空闲容量。

2.2 等效电量函数法误差分析

等效电量函数法的计算效率及误差大小与所采用的间隔大小有着密切的关系。间隔越大，计算效率越高，但可能影响随机生产模拟的精度。随机生产模拟的误差主要来源于以下2个方面：机组工作容量不是间隔的整数倍引起的误差；对持续负荷曲线等效引起的误差。

由式（2）和（9）可以看出，等效电量函数法要求所有的Ki均是整数（所有机组的容量均是所取间隔的整数倍）时方能保证算法的精确性。对于全容量分配的机组，其工作容量是已知值，可以通过选取合适的间隔使得Ki为整数。而对于存在空闲容量的水电机组，事实上其工作容量在随机生产模拟之前是未知的，故Ki很有可能不是整数，导致模拟过程中产生误差，针对这种情况，可以选取较小的间隔以减小误差。

随机生产模拟的基础是持续负荷曲线。等效电量函数法采用固定的间隔对持续负荷曲线进行积分，求出各间隔的等效电量，进而对电量进行卷积运算，其本质是对持续负荷曲线进行近似，近似过程中维持各间隔内的电量不变。此方法在分配机组电量、计算EENS或EDNS指标时能够保持很高的精度，但由于修改了持续负荷曲线，会导致计算LOLP指标时存在误差。

实际应用中，持续负荷曲线一般来源于负荷预测给出的时序负荷曲线。由于预测负荷为离散值，故持续负荷曲线是由离散点组成的台阶状曲线。以表1给出的某典型日预测负荷数据为例［18］，取间隔宽度为20 MW，图1给出了等效持续负荷曲线及等效电量函数法的说明图，图中横坐标为系统负荷，纵坐标为系统负荷大于等于横坐标值的概率。

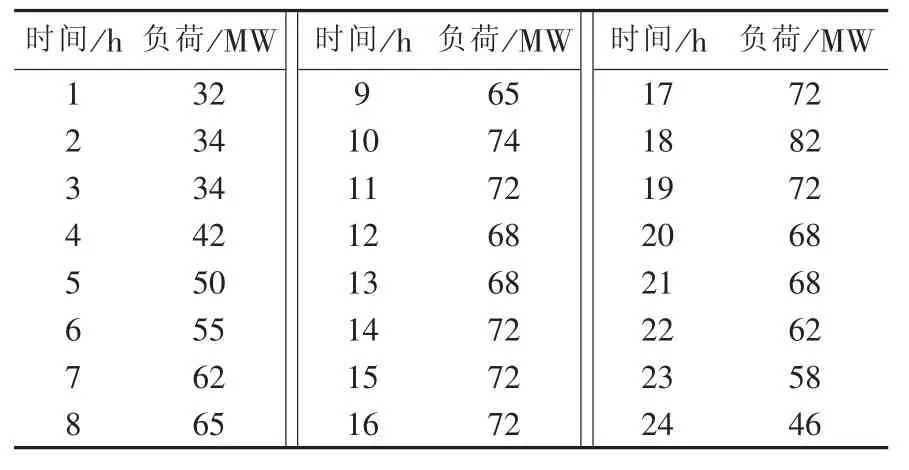
表1 某典型日预测负荷数据Table1 Forecasted load data for a typical day

图1 等效电量函数法说明图Fig．1 Illustration diagram of equivalent energy function method

如图1所示，等效电量函数法是采用虚线的等效持续负荷曲线代替实线的实际持续负荷曲线。等效持续负荷曲线被分隔成5块阴影部分，每块的面积正比于相应的电量（比例因子等于周期T）。等效电量函数法在进行卷积运算之前先采用等宽度的矩形对持续负荷曲线进行电量等效，但改变了持续负荷曲线的形状，影响了LOLP指标的计算精度。取较小的间隔可以减小等效持续负荷曲线的精度损失，提高LOLP指标的计算精度。以表1给出的时序负荷数据为例，当间隔取1 MW时，等效电量函数法描述的持续负荷曲线是精确的。

对于实际大规模电力系统而言，系统总负荷远大于单台机组的容量，一般比最小单机容量大2个数量级以上。由于负荷预测的精度还难以达到很高的水平，采用相同单位（如MW）时，预测负荷的小数点后位数一般不会多于机组容量的小数点后位数，负荷功率与机组容量的“最大公因子”一般等于机组容量的“最大公因子”。

2.3 两阶段定区间等效电量函数法

对于等效电量函数法而言，当采用以预测负荷及机组容量的“最大公因子”作为间隔时，安排降额运行的水电机组会由于间隔过大而产生较大的误差，导致LOLP指标的精度降低。为获得较高的计算精度就必须采用较小的间隔，这就意味着对所有机组的处理都采用小间隔，每次卷积的计算点数将大幅增加，随机生产模拟的计算量也将随之大幅增加。

随机生产模拟过程只有在所有火电机组均被安排运行之后，才会安排需要降额运行的水电厂。因为降额运行的水电厂带负荷顺序在所有火电机组和全容量分配的水电厂之后，故可以考虑将算法分成2阶段：第一阶段，即水火电协调分配阶段，水火电机组均按全容量进行模拟，采用预测负荷及机组容量的“最大公因子”作为间隔Δx1，以在不损失计算精度的前提下采用尽可能大的间隔，从而尽可能提高算法的计算效率；第二阶段安排降额运行的水电机组，由于无法事先确定机组工作容量，故需要采用较小的间隔Δx2，以提高算法的计算精度。两阶段定区间等效电量函数法的随机生产模拟流程如图2所示。

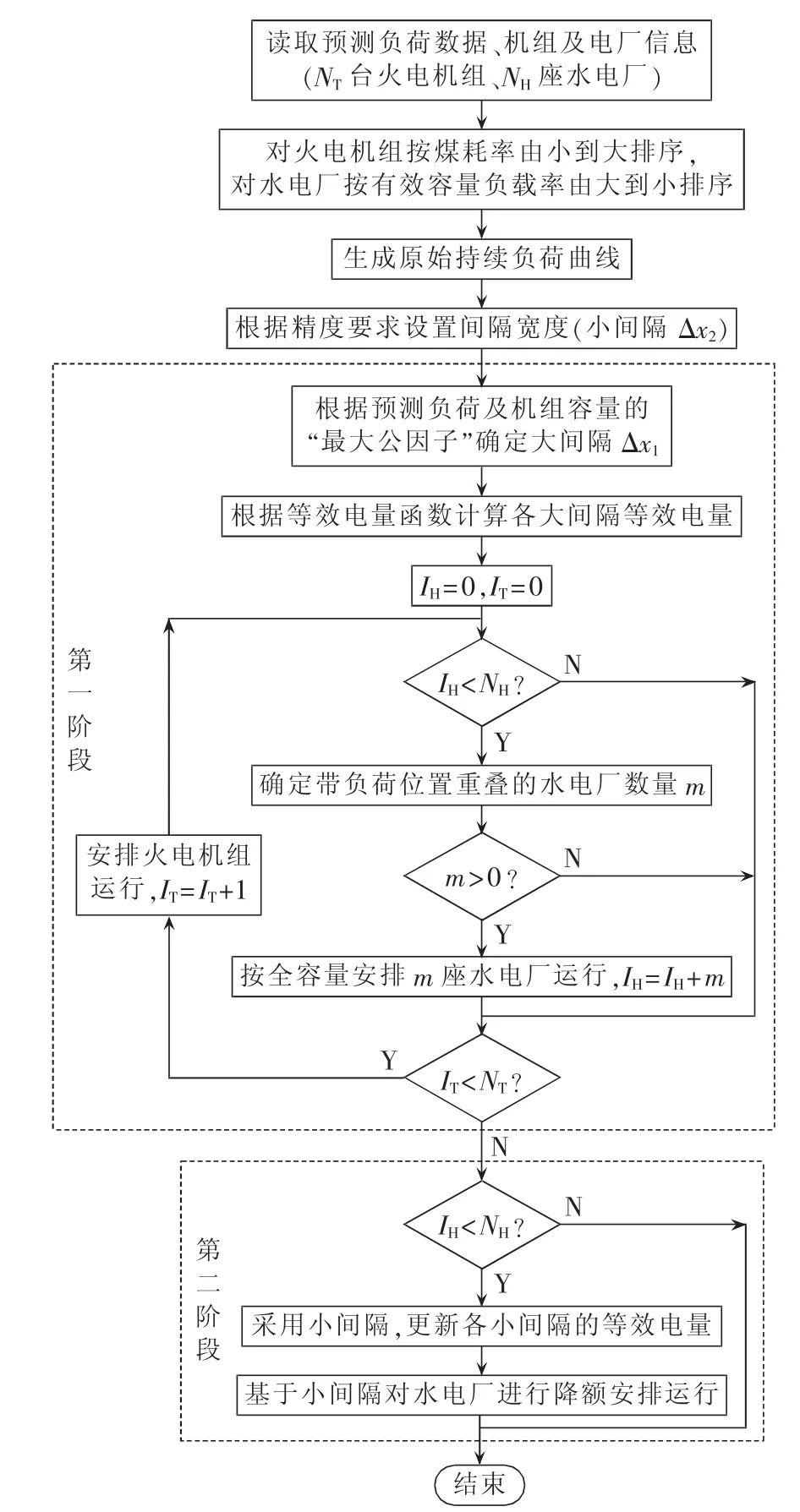
图2 基于两阶段定区间等效电量函数法的随机生产模拟流程图Fig．2 Flowchart of probabilistic production simulation based on two-stage fixed-range equivalent energy function method

由图2可以看出，在安排每台火电机组之前，都需要检验当前位置是否适合水电运行，即需要对所有水电厂进行试分配，故需要进行大量的卷积运算。根据“最大公因子”确定大间隔并进行模拟，可以在保证精度的同时大幅提高模拟效率。对于第二阶段而言，由于所有火电机组均已分配好电量，故不需要在水电与火电之间进行协调，所需的卷积运算次数相对较少，采用小间隔引起的附加计算量一般不大。

显然，当系统中所有的机组都以全容量安排运行时，即所有水电厂均没有空闲容量，则第二阶段模拟的水电厂数量为0，该情况可以看作是两阶段法的一个特例。另外，如果2个阶段采用的间隔相同，算法就退化为单个阶段。

3 算例分析

为了检验本文所提方法的有效性，采用C++编写了仿真测试程序，并采用传统等效电量函数法、定区间等效电量函数法及两阶段定区间等效电量函数法对IEEE-RTS 79修正及扩大系统进行随机生产模拟。仿真环境为Microsoft Visual Studio 2010，计算机配置为2.5 GHz CPU、8 GB内存。

为方便说明，下文将传统等效电量函数法简称为传统法，将定区间等效电量函数法简称为定区间法，将两阶段定区间等效电量函数法简称为两阶段法。对于传统法及定区间法，将所采用的间隔Δx称为基准单位；对于两阶段法，将第二阶段所采用的小间隔Δx2称为基准单位。

IEEE-RTS 79系统的电气及可靠性参数见文献［19］，该系统共有32台发电机，装机容量为3405 MW，总负荷为2 850 MW，总负荷及各机组容量的“最大公因子”为1 MW。文献［20］采用枚举法得到了IEEE-RTS 79系统中的发电系统可靠性指标的解析值。取基准单位为1 MW，表2给出了枚举法及3种等效电量函数法的可靠性指标计算结果。

表2 IEEE-RTS 79系统的发电系统可靠性指标计算结果Table 2 Reliability index calculation results of generation system in IEEE-RTS 79 system

从表2中可以看出，4种方法求得的可靠性指标完全一致（微小的差异仅在于保留的小数点后位数不同），这验证了3种等效电量函数法计算结果的准确性。

将IEEE-RTS 79系统中节点1、2、7假定为水电厂，并假定各水电厂的日电量计划如表3所示。表中，位于节点1的水电厂的有效容量负载率较大，目的是模拟水电厂与火电机组协调运行以安排经济带负荷位置的情况；而位于节点2、7的水电厂的有效容量负载率较低，目的是模拟水电厂因电量受限而存在空闲容量的情况。

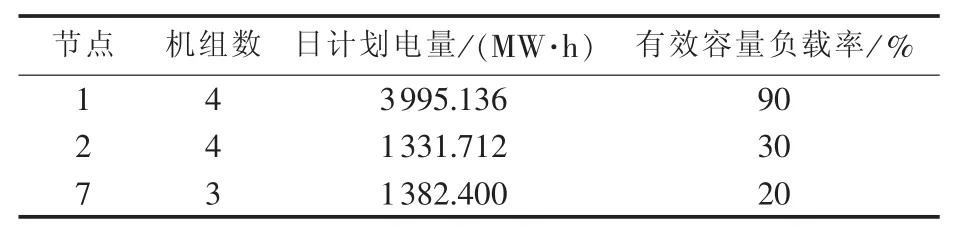
表3 各水电厂日电量计划Table 3 Daily electric energy schedules for hydropower plants

表4给出了不同基准单位下IEEE-RTS 79含水电厂的修正系统的随机生产模拟结果。同一基准单位下3种方法计算的EDNS和LOLP指标完全相同，故表中没有分别给出用各算法求得的指标值，这充分说明了本文所提方法的正确性。从表中可以看出，采用不同的基准单位，求得的EDNS指标均相同，这是由于机组容量“最大公因子”为基准单位的整数倍；基准单位越小，水电厂空闲容量及LOLP指标的计算精度越高，故基准单位决定了LOLP指标的计算精度。比较表2及表4的可靠性指标可以看出，增加了水电厂的定电量约束后，EDNS及LOLP指标值均变大，即可靠性水平变差。

表4 IEEE-RTS 79含水电厂修正系统的随机生产模拟结果Table 4 Probabilistic production simulation results of modified IEEE-RTS 79 system with hydropower plants

上述含水电的IEEE-RTS 79修正系统的机组数量较少，难以对算法的计算速度进行比较分析，为了更好地比较不同方法间的性能差异，将该系统扩大N倍（N个完全相同的系统通过足够强的联络线连在一起）后进行仿真分析。表5给出了N=10时不同基准单位下3种等效电量函数法的随机生产模拟结果。表6给出了基准单位取0.1 MW时不同计算规模下3种等效电量函数法的计算效率测试结果。

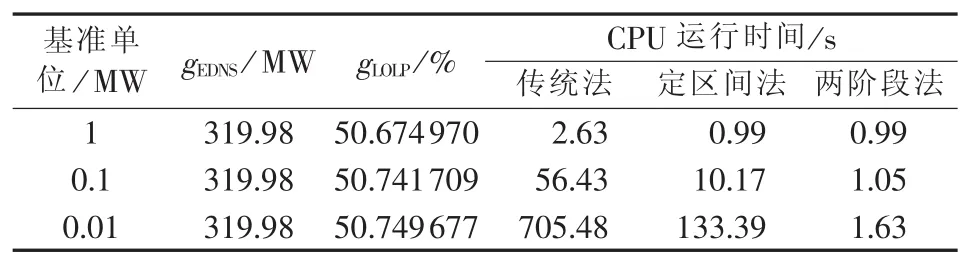
表5 IEEE-RTS 79含水电厂扩大系统的随机生产模拟结果Table 5 Probabilistic production simulation results of expanded IEEE-RTS 79 system with hydropower plants

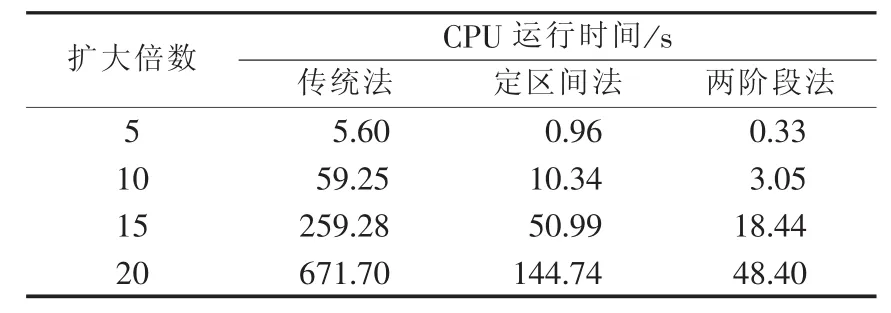
表6 不同规模系统的随机生产模拟效率测试结果Table 6 Efficiency test results of probabilistic production simulation under different system scales

从表5中可以看出，相同的基准单位下，定区间法所需的CPU运行时间均明显小于传统法，而两阶段法所需的CPU运行时间又明显小于定区间法（仅基准单位取1 MW时相同，这是由于两阶段法中Δx1=Δx2=1 MW，退化为定区间法）；随着基准单位的减小，精度要求提高，3种方法所花费的CPU运行时间均随之增加，传统法及定区间法所花费的CPU运行时间增加很快，对精度要求非常敏感，而两阶段法所花费的CPU运行时间增加较慢，对精度要求不敏感，比较适用于精度要求较高的场合。

从表6中可以看出，随着计算规模的增大，3种方法所花费的CPU运行时间均随之明显增大。计算规模相同时两阶段法所需的CPU运行时间均明显小于其他2种方法，具有更高的执行效率，能够更好地满足大规模水火发电系统高精度随机生产模拟的应用要求。

4 结论

本文分析了等效电量函数的有效区间及误差来源，基于此提出了用于水火发电系统随机生产模拟的两阶段定区间等效电量函数法，得到的主要结论如下：

a.通过对等效电量函数法的卷积公式引入平移变换，得到定区间等效电量函数法，可明显提高随机生产模拟效率；

b.在随机生产模拟的水火电机组协调阶段，根据系统负荷与机组容量的“最大公因子”确定尽可能大的间隔宽度，能够在不损失精度的同时大幅提高模拟效率；

c.在所有火电机组均带负荷之后的纯水电模拟阶段，算法所需的卷积次数较少，采用较小的间隔宽度，能够在不增加太多计算量的同时减小由于水电机组空闲容量引起的模拟误差；

d.两阶段定区间等效电量函数法所需的计算时间对小间隔的取值不敏感，比较适用于对LOLP指标计算精度要求较高的场合，能够更好地满足大规模水火发电系统高精度随机生产模拟的应用要求。

参考文献：

［1］于若英，高山.随机生产模拟在电力系统中的应用［J］.电力系统保护与控制，2012，40（11）：149-155.YU Ruoying，GAO Shan.Applications of probabilistic production simulation in power system［J］.Power System Protection and Control，2012，40（11）：149-155.

［2］LIU X，WANG H，ZHOU Q，et al.Power system probabilistic cost production simulation with wind power penetration based on multi-state system theory［C］∥2012 IEEE Power and Energy Society General Meeting.San Diego，USA：IEEE，2012：1-7.

［3］谢敏，陈金富，段献忠.非限能系统中考虑电价波动因素的随机生产模拟［J］. 电力自动化设备，2005，25（1）：12-17.XIE Min，CHEN Jinfu，DUAN Xianzhong.Probabilistic production simulation for non-limited energy system considering the fluctuation of electricity price［J］.Electric Power Automation Equipment，2005，25（1）：12-17.

［4］肖云鹏，王锡凡，王秀丽.基于随机生产模拟的直购电交易成本效益分析［J］. 电网技术，2016，40（11）：3287-3292.XIAO Yunpeng，WANG Xifan，WANG Xiuli.Cost and benefit analysison directelectricity purchase transaction based on probabilistic production simulation［J］.Power System Technology，2016，40（11）：3287-3292.

［5］STREMEL J P，JENKINS R T，BABB R A，et al.Production costing using the cumulant method of representing the equivalent load curve［J］.IEEE Transactions on Power Apparatus and Systems，1980，PAS-99（5）：1947-1956.

［6］WANG Xifan.Equivalent energy function approach to power system probabilistic modeling［J］.IEEE Transactions on Power Systems，1988，3（3）：823-829.

［7］谈天夫，高山，李海峰，等.考虑负荷分布变化的改进组合电力系统等效负荷持续曲线法［J］. 电力自动化设备，2014，34（12）：44-51.TAN Tianfu，GAO Shan，LI Haifeng，et al.Improved composite power system equivalent load duration curve method considering variation of load distribution［J］.Electric Power Automation Equipment，2014，34（12）：44-51.

［8］LEI J，WAN C L，CHEN H Y，et al.Studies on algorithms of power system probabilistic production simulation considering wind farms［C］∥2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference（APPEEC）.Xi’an，China：IEEE，2014：1-6.

［9］丁明，林玉娟，潘浩.考虑负荷与新能源时序特性的随机生产模拟［J］. 中国电机工程学报，2016，36（23）：6307-6314.DING Ming，LIN Yujuan，PAN Hao.Probabilistic production simulation considering time sequence characteristics of load and new energy［J］.Proceedings of the CSEE，2016，36（23）：6307-6314.

［10］吴雄，王秀丽，李骏，等．考虑风电外送的省级系统调峰分析模型［J］．电网技术，2013，37（6）：1578-1583．WU Xiong，WANG Xiuli，LI Jun，et al．A model to analyze peak load regulation of provincial power system considering sending-out of wind power［J］．Power System Technology，2013，37（6）：1578-1583．

［11］王锡凡. 电源优化模型［J］.西安交通大学学报，1986，20（2）：1-12.WANG Xifan.Optimalgenerating system planning model［J］.Journal of Xi’an Jiaotong University，1986，20（2）：1-12.

［12］王锡凡.包含多个水电机组的电力系统随机生产模拟［J］.西安交通大学学报，1985，19（4）：69-82.WANG Xifan.Probabilisticsimulation ofmultipleassignedenergy hydroelectric units［J］．Journal of Xi’an Jiaotong University，1985，19（4）：69-82．

［13］李林川，王锡凡，王秀丽.基于等效电量函数法的互联电力系统随机生产模拟［J］. 中国电机工程学报，1996，16（3）：180-184.LI Linchuan，WANG Xifan，WANG Xiuli．Probabilistic modeling forinterconnected powersystemsbased on the equivalent energy function approach［J］．Proceedings of the CSEE，1996，16（3）：180-184.

［14］冯长有，梁志峰.考虑潮流断面约束的电力系统随机生产模拟［J］. 电网技术，2013，37（2）：493-499.FENG Changyou，LIANG Zhifeng.Powersystem probabilistic production simulation considering constraints of tie line power flows［J］.Power System Technology，2013，37（2）：493-499.

［15］王锡凡.电力系统随机生产模拟的等效电量函数法［J］.西安交通大学学报，1984，18（6）：13-26.WANG Xifan.EEF approachtopowersystem probabilistic modeling［J］.Journal of Xi’an Jiaotong University，1984，18（6）：13-26.

［16］丁明，楚明娟，毕锐，等.基于序贯蒙特卡洛随机生产模拟的风电接纳能力评价方法及应用［J］. 电力自动化设备，2016，36（9）：67-73.DING Ming，CHU Mingjuan，BI Rui，et al.Wind power accommodation capability evaluation based on sequential Monte Carlo probabilistic production simulation and its application［J］.Electric Power Automation Equipment，2016，36（9）：67-73.

［17］ZHANG H Y，ZHU H J，SHEN H，etal.Theprobabilistic production simulation for mixed wind-hydro-thermal power system and the sensitivity analysis for the indices of abandoned wind［C］∥2012 Asia-Pacific Power and Energy Engineering Conference.Shanghai，China：IEEE，2012：1-4.

［18］丘文千.电力系统优化规划模型及方法［M］.杭州：浙江大学出版社，2012：211-212.

［19］Reliability Test System Task Force of the Application of Probability Methods Subcommittee.IEEE reliability test system ［J］.IEEE Transactions on Power Apparatus and Systems，1979，98（6）：2047-2054.

［20］侯雨伸，王秀丽，刘杰，等.基于拟蒙特卡罗方法的电力系统可靠性评估［J］. 电网技术，2015，39（3）：744-750.HOU Yushen，WANG Xiuli，LIU Jie，et al.A quasi-Monte Carlo method based power system reliability evaluation［J］.Power System Technology，2015，39（3）：744-750.