开关变换器功率电感磁损建模及应用

周 岩，张俊波，陈麒米

（南京邮电大学 自动化学院，江苏 南京 210023）

0 引言

在高频开关变换器中磁性元件主要用作变压器和功率电感。近年来，随着开关变换器向小型化、高频化的方向发展，对磁性元件中的磁芯损耗进行预估越来越受重视。功率磁性元件对开关变换器的性能和可靠性有着决定性的影响，不合理的磁性元件设计会引起磁芯的显著温升，进而引起开关变换器工作失效［1］。

开关频率f、磁通密度变化量Bpp、占空比D、直流偏磁HDC、温度T等都会对磁性元件的功率磁损产生直接的影响，这给磁芯损耗的建模带来了困难。即使在Bpp相同的条件下，磁芯损耗也会受到直流偏磁HDC和激励波形变化的显著影响［2-20］。目前，工程中普遍采用基于实验数据拟合的Steinmetz方程。经典的Steinmetz方程是通过3个系数拟合磁芯材料在正弦激励条件下不同频率和磁通密度时的损耗值，具有参数少、应用简单的优点。由于开关变换器中磁性元件承受的激励为占空比变化的矩形波，故许多学者提出采用如MSE、GSE、iGSE等Steinmetz方程修正模型来分析非正弦激励条件下的磁芯损耗［2-8］。但由于Steinmetz修正方程修正模型中的拟合系数受到磁性材料、T、f、HDC和Bpp的显著影响，故需要大量的测试数据才能得到特定工作条件下的损耗系数。另外，基于Steinmetz方程修正模型仅能得到相同磁通密度变化量Bpp条件下的矩形波损耗系数，而大多数功率磁芯中的Bpp是变化的。如果考虑到直流偏磁对磁芯损耗的影响，还需要进一步修正Steinmetz方程模型，变得过于复杂。基于物理机理的磁芯损耗模型主要有Jiles-Atherton磁滞模型、Preisach磁滞模型和Bertotti磁芯损耗分离模型［9-12］。磁损物理模型为开关变换器在各类工况下的磁性元件损耗建模分析提供了理论基础，但其主要缺点是模型中包含过多的材料参数，给实际应用带来了困难。

为了克服传统磁损物理模型中材料系数过多的缺点，本文结合磁芯损耗产生的物理机理和开关变换器电路工作特征，建立了功率电感磁芯损耗计算模型。首先系统地介绍了不同因素对磁滞损耗和涡流损耗的影响；以Buck、Boost变换器功率电感为例，结合电路的工作原理，给出了功率电感在不同条件下的磁芯损耗计算方法。本文所提计算模型无需依赖任何磁芯材料系数，仅需要测量一组正弦激励条件下的损耗数据就可预测矩形波激励下的磁损，这对于分析开关变换器中功率电感的磁芯损耗具有重要的工程应用价值。

1 磁芯损耗物理模型

磁芯材料在交变磁场作用下会产生损耗，根据Bertotti磁芯损耗构成理论可知，磁芯损耗Pv主要由磁滞损耗Ph、涡流损耗Pc和剩余损耗Pex三部分组成［10］。

1.1 磁滞损耗

磁性元件中的磁畴在外磁场的作用下会发生转动，部分磁畴转动时需要克服磁畴壁的摩擦力而消耗能量，从而产生磁滞损耗。在单个磁化周期内，静态磁滞损耗的大小与磁通密度变化量相关，可等效为磁滞回线包围的面积，且磁滞损耗与频率成正比。在强磁场激励下，磁滞损耗可近似表示为：

其中，f为磁芯所承受的开关频率。

文献［20］给出了直流偏置对磁滞损耗影响的等效物理模型，证明了在直流偏置条件下磁滞损耗的大小与开关频率依然满足线性关系，具体如下：

其中，ch为磁滞损耗系数。

同时，文献［20］证明了在相同 Bpp、HDC和 f的条件下，不同激励波形所造成的磁滞损耗是相同的，即：

1.2 涡流损耗

由于交变磁场在磁芯中会产生感应电压，且铁氧体等磁性材料存在等效电阻，故交变磁场在磁芯材料中会产生感应电流，其所消耗的能量就是涡流损耗。磁芯涡流损耗的大小与激励的波形紧密相关。单位涡流损耗的一般表达式为：

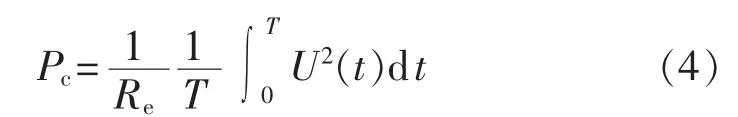
其中，Re为磁芯等效电阻；U（t）为每个开关周期激励电压。在相同工作条件下，正弦激励涡流损耗和方波激励涡流损耗之间的数学关系为［18］：

在正弦激励条件下，磁芯涡流损耗与频率的关系为：

其中，cc为涡流损耗系数。

1.3 剩余涡流损耗

剩余涡流损耗是由于磁芯材料中磁畴之间的磁畴壁随外磁场变化所产生的损耗。与典型涡流损耗相比，剩余涡流损耗在低频或低磁通密度工作条件下占主导。考虑到功率磁芯工作在高频、高磁通密度条件下，忽略剩余涡流损耗可简化计算且不会带来显著误差［11］，因此，对于估算工作在高频、高磁通密度条件下的磁性元件，磁芯损耗与频率的关系可进一步简化为［16-18］：

在相同的Bpp和HDC条件下，测量2个相邻不同频率点fA、fB的正弦磁损数据可分离出相应频率点的磁滞损耗和涡流损耗分量［17，20］，具体如下：

2 影响磁芯损耗的关键因素

由于影响磁芯损耗的因素有很多，分析不同因素对磁损的具体影响，对于设计磁性元件合理的工作区间具有重要意义。

2.1 f和Bpp对磁芯损耗的影响

由式（2）和（6）可知，磁滞损耗 Ph与 f成正比，涡流损耗Pc与f呈平方关系。当Bpp较大时，磁滞损耗Ph和涡流损耗Pc均与Bpp呈平方关系。可见，f、Bpp的增大将会导致磁芯损耗的急剧增加。

2.2 HDC对磁芯损耗的影响

开关变换器中部分变压器和滤波电感在工作时均存在一定的偏置电流Idc，如图1所示。图中，Io为功率电感中的平均电流；ΔI为功率电感上脉动电流绝对值；Im为电流幅值。

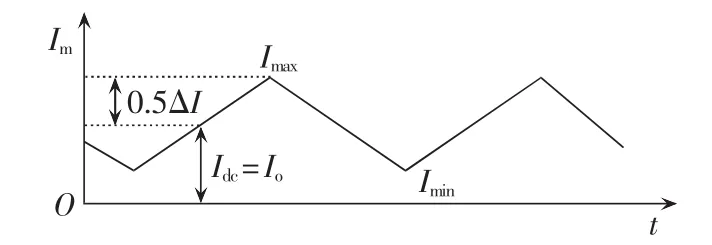
图1 磁芯电流波形图Fig.1 Waveform of core current

直流偏置电流Idc对磁滞损耗Ph的影响主要体现在对单位周期内静态磁滞回线面积的影响。因此即使Bpp保持不变，磁滞损耗也会随着直流偏磁的增大而显著增加，文献［20］已给出了详细的物理模型。直流偏置电流Idc对涡流损耗分量Pc也会产生显著影响。这主要是由于磁芯材料的等效电阻率ρ与磁芯工作的磁场强度区间相关。由于HDC导致磁芯工作区间变化，进而引起ρ的改变，使得涡流损耗发生变化。

2.3 D对涡流损耗的影响

开关变换器的磁性元件一般工作在非正弦的矩形电压激励下。为了获得稳定的输出电压，开关变换器需要根据输入电压的变化调节占空比。由于磁通密度变化率dB／dt的变化，即使磁通密度变化量Bpp相同，当占空比较小时涡流损耗也会显著增加［12，18］。

2.4 温度对磁芯损耗的影响

磁芯损耗随温度变化会产生显著的非线性变化。需要注意的是，厂家针对不同的温度应用场合会推出不同的磁芯材料，考虑到实际开关变换器中磁芯的工作条件，一般选择在100℃左右时产生磁损最低的磁芯。

3 Buck和Boost变换器功率电感损耗特征

本文以Buck和Boost变换器为例，详细讨论基于磁损分离模型和开关变换器电路工作原理的建模方法。在磁性元件设计中，主要关心的是在最恶劣工况条件下的磁损变化趋势，也就是在最大输出电流条件下、占空比变化时的磁损变化趋势。因此本文主要分析开关变换器工作在连续导通模式（CCM）下的磁芯损耗。

为了保证输出电压不变，开关变换器输入电压的变化将会引起D和Bpp的改变，进而引起磁芯损耗的显著变化。

3.1 Buck变换器工作原理

Buck变换器主电路如图2所示。

图2 Buck变换器主电路Fig.2 Main circuitry of Buck converter

设定Buck变换器工作在CCM，在VT1导通期间电感正向激磁，磁通变化量为：

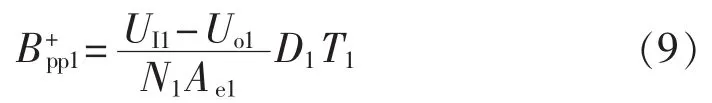
其中，N1为线圈匝数；Ae1为磁芯截面积。

在VT1截止期间电感反向退磁，磁通变化量为：

输入电压UI1与输出电压Uo1的关系为：

3.2 Buck变换器磁芯损耗特征

结合式（4）、（9）—（11）可知，Buck 变换器单位体积磁芯中的涡流损耗可表示为：

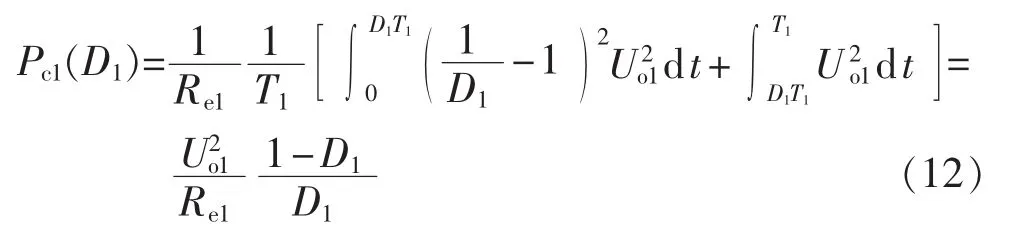
由式（12）可知，不同占空比条件下涡流损耗与占空比为0.5方波激励下的涡流损耗的关系为：

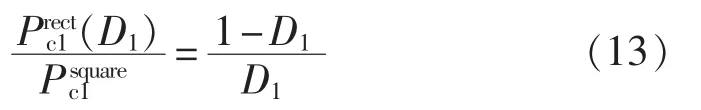
令D1=0.5时涡流损耗为1，不同占空比条件下磁芯的涡流损耗变化趋势如图3所示。可见，随着占空比的增大，涡流损耗显著降低。

图3 涡流损耗与D1的关系曲线Fig.3 Curve of core loss vs.D1

由式（5）和（13）可知，正弦波和方波激励下的涡流损耗的关系为：

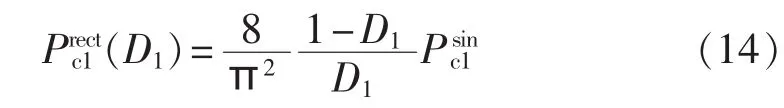
设定占空比为0.5时Bpp1为1，由式（10）可知占空比的变化会引起Bpp1的变化，随着占空比的增大磁滞损耗线性下降，具体如图4所示。

由式（1）和（10）可知，矩形波激励下的磁滞损耗与占空比为0.5方波激励下的磁滞损耗的关系为：

图4 Bpp与D1的关系曲线Fig.4 Curve of Bppvs.D1

设D1=0.5时磁滞损耗为1，磁滞损耗与D1之间的变化趋势如图5所示。可见，磁滞损耗会随着占空比的增加而迅速减小。

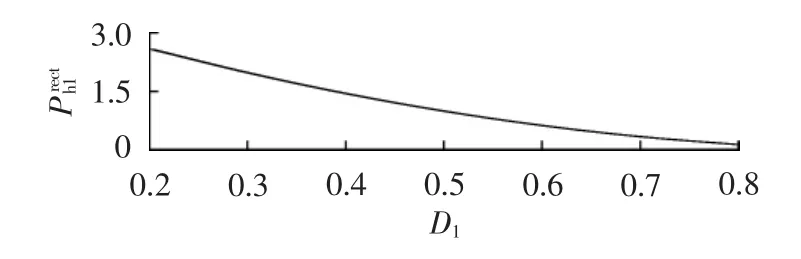
图5 磁滞损耗与D1的关系曲线Fig.5 Curve of hysteresis loss vs.D1

结合式（3）、（14）和（15）可知，不同占空比条件下Buck变换器功率磁芯损耗为：

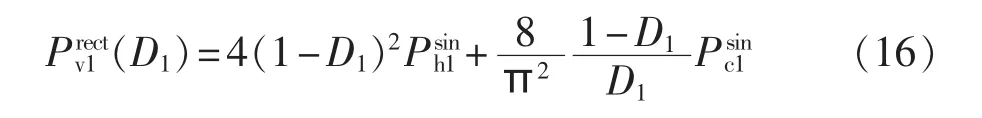
4 Boost变换器磁芯损耗

4.1 Boost变换器基本原理与工作

Boost变换器主电路如图6所示。

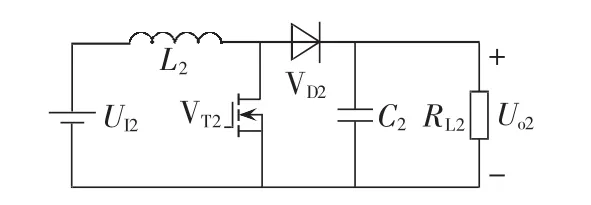
图6 Boost变换器主电路Fig.6 Main circuitry of Boost converter

在VT2导通期间电感正向激磁，磁通变化量为：

在VT2截止期间电感反向退磁，磁通变化量为：

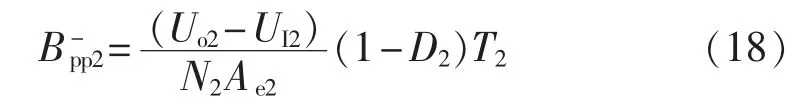
输入电压UI2与输出电压Uo2的关系为：

4.2 Boost变换器磁芯损耗的典型特征

结合式（4）、（17）—（19）可知，Boost变换器磁芯中的涡流损耗可以表示为：

当Boost变换器占空比变化时，涡流损耗与占空比为0.5方波激励下的涡流损耗的关系为：

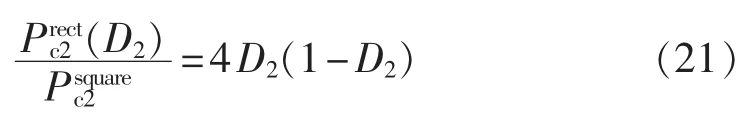
设D2=0.5时涡流损耗为1，则D2对涡流损耗的影响如图7所示。可见，D2=0.5时，磁芯的涡流损耗最大；随着D2的增加或减小，涡流损耗都会降低。

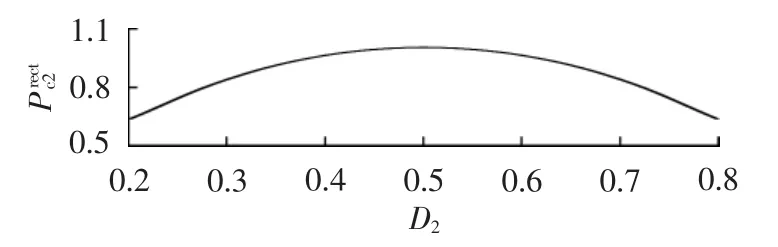
图7 涡流损耗与D2的关系曲线Fig.7 Curve of core loss vs.D2

由式（5）和（21）可知，正弦波和方波激励下的涡流损耗的关系为：

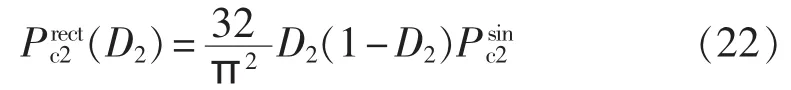
由式（18）和（19）可知，Boost变换器中 Bpp2为：

设定D2=0.5时Bpp2为1，则占空比变化引起Bpp2变化的具体关系如图8所示。

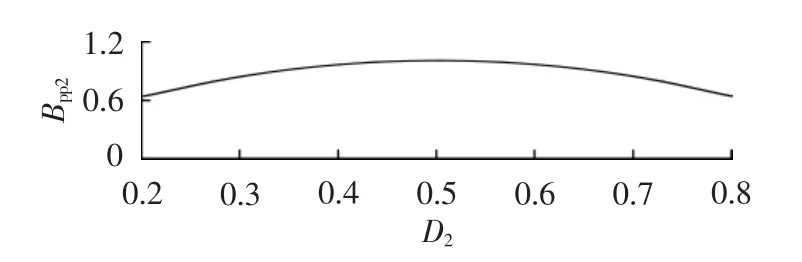
图8 Bpp与D2的关系曲线Fig.8 Curve of Bppvs.D2

设占空比D2=0.5时磁滞损耗为1，则不同占空比对磁滞损耗的影响如图9所示。

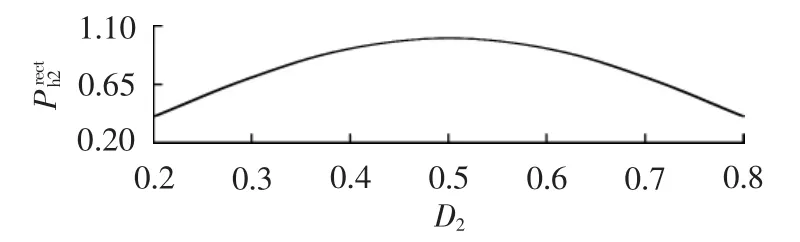
图9 磁滞损耗与D2的关系曲线Fig.9 Curve of hysteresis loss vs.D2

由式（3）、（22）和（24）可知，不同占空比条件下Boost变换器功率磁芯损耗为：

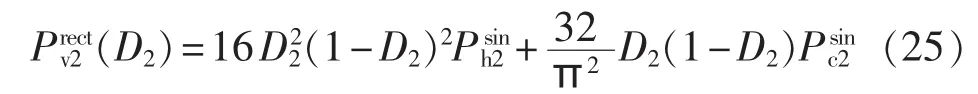
5 实验验证

磁芯损耗测试平台见图10。采用ArbExpress软件编辑所需的任意激励波形信息，并将波形信息发送给信号发生器Tektronix AFG3022B，产生相应激励信号［19］；通过调节功率放大器 Krohn-HITE 7500 的放大倍数，控制磁芯电感两端激励电压的大小，产生所需的磁通密度；直流电源与去耦电感LD串联，在磁芯绕组N31上施加直流偏磁。测试磁芯采用双线圈并联绕线方式，功率分析仪YOKOGAWA WT1800通过采集N11绕组电流和N22绕组电压，计算出磁芯损耗。实验中，选取的是Ferroxcube公司的3C90铁氧体磁环 TX40 ／24 ／16，线圈绕组为 N11∶N21∶N31=6∶6∶1。

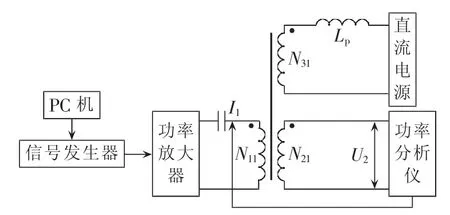
图10 磁芯损耗测试平台Fig.10 Testing platform of core losses

设定Buck变换器的工作条件如下：开关频率为100 kHz，直流偏磁为 12.5 A／m，占空比的变化范围为0.2～0.8。占空比为0.5时，磁通密度变化量为0.16T。

测量相同磁通密度变化量和直流偏磁时50 kHz和100 kHz正弦激励下的磁损数据，根据式（9）分离出100 kHz时的磁滞损耗分量和涡流损耗分量。表1列出了所测得的磁损数据和计算得到的磁损成分分量。

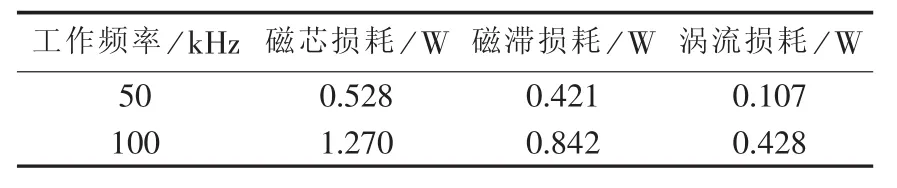
表1 Buck变换器功率电感实验结果Table 1 Experimental results of power inductor in Buck converter

根据表1数据和式（16），图11给出了不同占空比下Buck变换器磁芯损耗预估值与实测值比较结果。可见Buck变换器中的磁损随着占空比的增大而显著降低，实验数据与预测值吻合。

图11 Buck变换器磁芯损耗预估值与实测值比较Fig.11 Comparison between predicted and true data of core losses in Buck converter

设定Boost变换器的工作条件如下：开关频率为100 kHz，直流偏磁为12.5 A／m，占空比的变化范围为0.2～0.8。当占空比为0.5时，磁通密度变化量为0.2 T。

同样地，测量相同磁通密度变化量和直流偏磁时50 kHz和100 kHz正弦激励磁损数据，根据式（9）分离出磁滞损耗分量和涡流损耗分量。表2列出了所测得的磁损数据和计算得到的磁损成分分量。

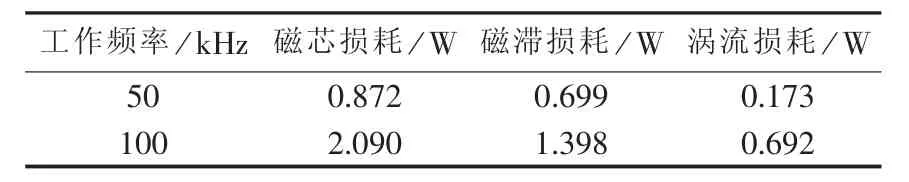
表2 Boost变换器功率电感实验结果Table 2 Experimental results of power inductor in Boost converter

根据表 2的数据和式（25），图12给出了不同占空比下Boost变换器磁芯损耗预估值与实测值比较结果。可见Boost变换器在占空比为0.5时磁芯损耗最大，随着占空比的增大或减小磁芯损耗显著降低。实验数据与预测结果变化趋势基本吻合。

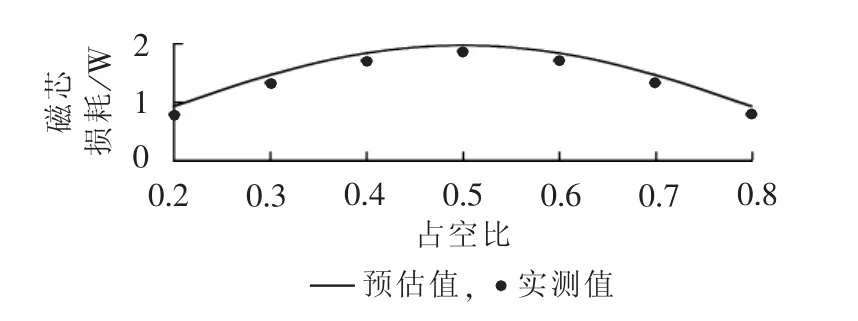
图12 Boost变换器磁芯损耗预估值与实测值比较Fig.12 Comparison between predicted and true data of core losses in Boost converter

6 结论

开关变换器中的功率电感一般工作在带有直流偏置电流的矩形电压波激励条件下。本文以Buck、Boost变换器中的功率电感为例，结合磁芯损耗产生的物理机理和电路工作特征，对功率电感磁芯损耗进行建模分析。本文系统地介绍了占空比、直流偏置对磁滞损耗分量和涡流损耗分量的影响，给出了不同工作条件下磁芯损耗的变化规律。整体建模过程总结如下。

a.确定磁芯的工作条件。如根据输入电压、输出电压确定磁芯工作的占空比范围；根据最大输出电流确定直流偏置条件；计算占空比为0.5时的Bpp。

b.测量正弦磁损数据。根据步骤a所确定的f、Idc和Bpp条件下的正弦损耗数据，分离出相应的磁滞损耗分量和涡流损耗分量。

c.预估工作区间内的磁损。根据步骤b所确定的磁损分量，结合Buck和Boost变换器电路工作特征确定占空比变化时的磁损变化趋势。

上述模型简单实用，且实验表明所提出的磁损分析模型能够满足工程应用精度。同时，本文中所提的磁损建模思路同样可适用于任意开关变换器拓扑，建模方法具有一般性。

参考文献：

［1］叶曙光，胡蕊，刘钊，等.基于LCL滤波器的双向储能变流器研究［J］. 电力自动化设备，2014，34（7）：88-92.YE Shuguang，HU Rui，LIU Zhao，etal.Bi-directionalpower conversion system based on LCL filter［J］.Electric Power Automation Equipment，2014，34（7）：88-92.

［2］叶建盈，陈为，汪晶慧.PWM波及直流偏磁励磁下磁芯损耗模型研究［J］. 中国电机工程学报，2015，35（10）：2601-2606.YE Jianying，CHEN Wei，WANG Jinghui.Research on the core loss model under PWM wave and DC bias excitations［J］.Proceedings of the CSEE，2015，35（10）：2601-2606.

［3］曹林，何金良，张波．直流偏磁状态下电力变压器铁心动态磁滞损耗模型及验证［J］．中国电机工程学报，2008，28（24）：141-146．CAO Lin，HE Jinliang，ZHANG Bo.Dynamic hysteresisloss model of power transformer under DC current biasing and its verification［J］.Proceedings of the CSEE，2008，28（24）：141-146．

［4］龚宇，崔巍，章跃进．考虑局部磁滞损耗的复合电机铁损耗计算［J］．中国电机工程学报，2014，34（30）：5396-5400．GONG Yu，CUI Wei，ZHANG Yuejin.Iron loss calculation of compound motors considering minor hysteresis losses［J］.Proceedings of the CSEE，2014，34（30）：5396-5400．

［5］张艳丽，李玉梅，刘洋，等．考虑不同磁特性模型的感应电机铁心损耗分析［J］．中国电机工程学报，2013，33（27）：120-126．ZHANG Yanli，LI Yumei，LIU Yang，et al.Analysis of core losses in induction motors considering different magnetic property models［J］.Proceedings of the CSEE，2013，33（27）：120-126．

［6］夏向阳，孔祥霁，帅智康，等.基于磁集成结构DC-DC变换器的超级电容储能系统［J］. 电力自动化设备，2014，34（11）：95-99.XIA Xiangyang，KONG Xiangji，SHUAIZhikang，etal.Supercapacitor energy storage system based on DC-DC converter［J］.Electric Power Automation Equipment，2014，34（11）：95-99.

［7］MUHLETHALER J，BIELA J，KOLAR J W，et al．Core losses under the DC bias condition based on Steinmetz parameters［J］．IEEE Transactions on Power Electronics，2012，27（2）：953-963．

［8］MUHLETHALER J，BIELA J，KOLAR J W，et al．Improved coreloss calculation for magnetic components employed in power electronic systems［J］．IEEE Transactions on Power Electronics，2012，27（2）：964-973．

［9］MAYERGOYZ I D，FRIEMAN G．Generalized preisach model of hysteresis（invited）［J］．IEEE Transactions on Magnetics，1988，24（1）：212-217．

［10］BERTOTTI G.General properties of power loss in soft magnetic material［J］．IEEE Transactions on Magnetics，1988，24（1）：621-630.

［11］ROSHEN W A.Ferrite core loss for power magnetic components design［J］．IEEE Transactions on Magnetics，1991，27（6）：4407-4415.

［12］ROSHEN W A.A practical，accurate and very general core loss model for nonsinusoidal waveforms［J］.IEEE Transactions on Power Electronics，2007，22（1）：30-40.

［13］SASAKI Y，MATSUKI T.Hysteresis loss in Mn-Zn ferrites［J］．IEEE Transactions on Magnetics，1986，22（5）：623-625.

［14］SEIICHI Y，ETSUO O，TSUTOMU O.AC resistivity of Mn-Zn ferrites［C］∥IEEE Intelec Conference Record.Kyoto，Japan：IEEE，1991：703-708.

［15］LIN D，ZHOU P，FU W N，et al．A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis［J］．IEEE Transactions on Magnetics，2004，40（2）：1318-1321．

［16］周岩，杨长业.高频铁氧体功率损耗分离方法及其应用［J］.磁性材料及器件，2013，44（6）：50-54.ZHOU Yan，YANG Changye.Separation of high frequency ferrite core power loss and its application［J］.Journal of Magnetic Materials and Devices，2013，44（6）：50-54.

［17］ZHOU Yan，SUN Aiming.A simplified ferrite core loss separation model for switched mode power converter［J］.IET Power Electronics，2016，9（3）：529-535.

［18］周岩.高频矩形波激励下磁芯损耗的研究［J］.电力自动化设备，2013，33（1）：91-95.ZHOU Yan.Magnetic core loss excited by high-frequency rectangle waveform［J］.Electric Power Automation Equipment，2013，33（1）：91-95.

［19］周岩，孙爱鸣，张俊波，等.基于ArbExpress软件的开关变换器典型激励波形生成方法研究［J］. 电测与仪表，2016，53（5）：11-15.ZHOU Yan，SUN Aimin，ZHANG Junbo，et al.The research on how to generate typical excitation waveforms based on ArbExpress in the switching converter［J］.Electrical Measurement&Instrumentation，2016，53（5）：11-15.

［20］ZHOU Yan，CHEN Qimi.Predicting core losses under the DC bias based on the separation model［J］.IEEE Journal of Emerging and Selected Topicsin PowerElectronics，2017，5（2）：833-840.