基于阻尼转矩分析法的UPFC阻尼通道选取与附加稳定器的协调设计

任必兴 ，杜文娟 ，王海风 ，黄俊辉 ，张 琰 ，王相锋，蔡 晖

（1.华北电力大学 电气与电子工程学院，北京 102206；2.国网江苏省电力公司经济技术研究院，江苏 南京 210008）

0 引言

统一潮流控制器UPFC（Unified Power Flow Controller）的概念由美国西屋科技中心的L.Gyugyi博士首先提出，是迄今为止FACTS（Flexible AC Transmission Systems）家族中性能最强的一种综合补偿器，其成功投入商业化运行被称为FACTS技术发展的重要里程碑。中国第一台UPFC于2015年底在江苏南京建成并投入商业运行［1］。

电力系统中装设FACTS装置通常是实现电压支撑、潮流控制等作用。在FACTS装置上附加稳定器，不仅能够有效抑制区域内低频振荡（功能类似发电机电力系统稳定器（PSS）），还能够有效抑制系统区间振荡［2-5］。基于复频率域的阻尼转矩分析（DTA）法是建立在发电机转子运动所获得的阻尼转矩这一实际概念上，能够清晰看到稳定器提供阻尼的产生、传递和分配过程，并成功应用于FACTS装置和储能系统的安装定位与稳定器参数设计［6-8］。电力系统中若采用相位补偿法设计多个稳定器，极易导致稳定器之间发生负交互作用，影响总体控制效果。因此，很多学者致力于稳定器协调设计研究［9-12］。

本文在关于UPFC提高系统低频振荡稳定机理研究的基础上［4-5］，将文献［13］中主要针对发电机 PSS的DTA方法延伸至包含UPFC的多机电力系统，并提出了基于DTA的UPFC最佳阻尼通道选取方法。鉴于UPFC多个控制回路可安装多个稳定器以抑制多个低频振荡模态，本文结合DTA指标有效定位UPFC多个阻尼通道，提出一种UPFC多个稳定器的协调优化算法，仿真算例验证了所提方法的有效性。

1 UPFC基本结构与控制策略［4-5］

UPFC的主要工作原理是通过电压源逆变器（VSC）及控制系统来改变串联变压器的输出电压的幅值与相角，从而起到调节线路潮流和支撑电压的作用。UPFC的基本结构与控制策略如图1所示，它主要由串联变压器、并联变压器、串联VSC、并联VSC及其共用直流电容器组成。

图1 UPFC原理图Fig.1 Schematic diagram of UPFC

从图1可见，UPFC装设在线路节点1和2之间，用来控制线路上的有功和无功功率S=P+jQ，同时调节并联连接点的电压幅值UEt。图中，Cdc为UPFC电容参数；Udc为UPFC直流电容电压；xE和xB分别为UPFC并联侧、串联侧变压器的等效电抗；UE和UB分别为UPFC并联、串联侧VSC的端口电压；me、mb和δe、δb分别为并联、串联侧VSC端口电压的幅值调制比率和相角［4-5］。一般采用比例-积分（PI）控制器构成UPFC的主控制回路，UPFC总共有4对控制变量，即 me-UE、δe-Udc、mb-Q 和 δb-P。

在UPFC主控制回路上附加稳定器，能有效提高系统阻尼，抑制低频振荡。UPFC附加稳定器结构见图2。图中，X 为UPFC的 4个控制目标量（UEt、Udc、Q和P）的统称；KPSS为稳定器增益；T1—T4为稳定器时间常数；XPSS为稳定器输出信号；XIN为稳定器输入信号，一般取本地线路功率；Δ表示各量的变化量。

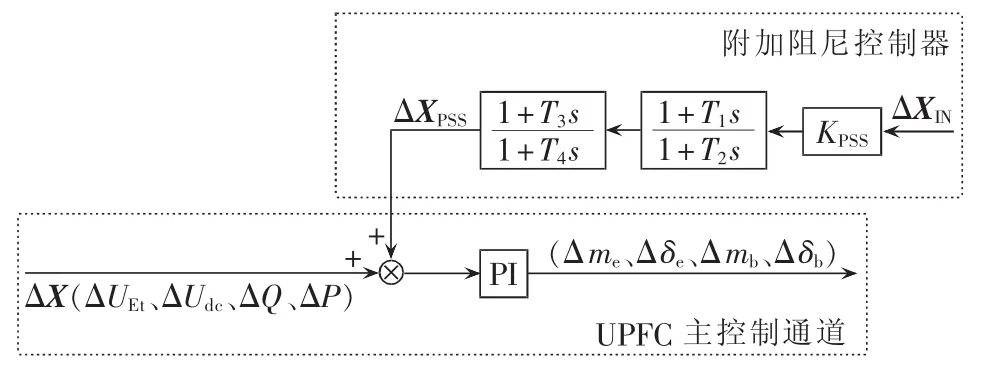
图2 UPFC附加稳定器框图Fig.2 Block diagram of auxiliary stabilizer added to UPFC

在主控制器闭环的情况下考虑附加阻尼信号的引入，UPFC的线性化方程为：

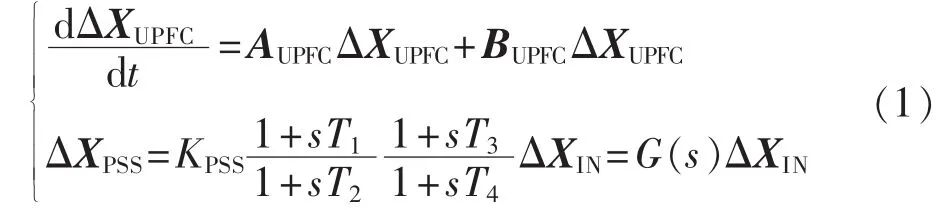
其中，状态变量XUPFC为UPFC的全部状态量（包含电容电压状态量，以及 PI控制器输出量 me、δe、mb和δb，详见文献［4-5］）；G（s）为稳定器传递函数。

通过网络代数方程接口，将UPFC线性化方程与发电机状态方程整合，得到含UPFC的全系统线性化方程［13］：

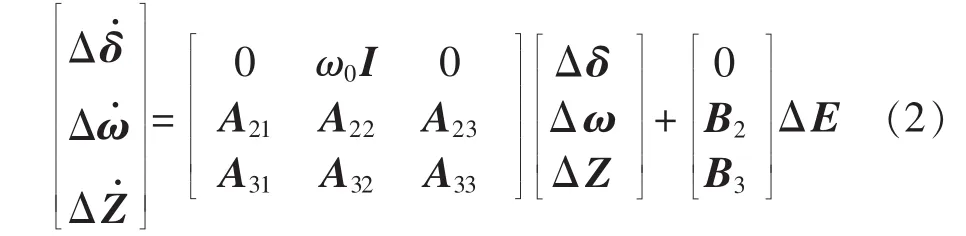
其中，δ为发电机功角状态变量向量；ω为发电机转速状态变量；Z为除了功角和转速之外的发电机状态变量，还包括UPFC自身的状态变量；E为稳定器变量；ω0I 为对角阵，ω0为额定角速度；A21、A22、A23、A31、A32、A33为分块矩阵；B2和 B3为输出分块矩阵。

2 含UPFC的系统DTA理论

UPFC附加阻尼控制信号到发电机机电振荡环节的前向通道为［13］：

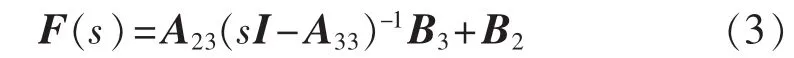
依据线性控制理论，可用各台发电机的转速状态变量Δω重构稳定器输出信号：

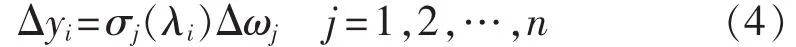
其中，λi为目标机电振荡模态；Δωj为全部n台发电机中的第j台发电机的转速变量；σj（λi）为重构系数。

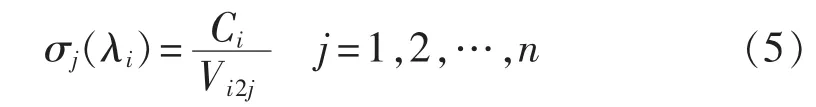
其中，Vi2j为Vi中对应于 Δωj的分量，Vi为对应于 λi的右特征向量；Ci为传递函数对应于λi的分量。

针对机电振荡模态λi，稳定器向系统中第j台发电机机电振荡回路提供的阻尼转矩系数Dij为：

式（6）表明稳定器向每一台发电机都提供阻尼转矩。其中，MjFj（λi）σj（λi）=Hij∠φij，Hij和 φij分别为目标模态λi下稳定器向第j台发电机提供阻尼贡献的幅值和相角；Mj为第j台发电机的惯性常数。

定义Sij为λi的阻尼对第j台发电机机电振荡回路提供的阻尼转矩系数Dij的灵敏度［13］：

UPFC附加阻尼控制的DTA指标定义为：

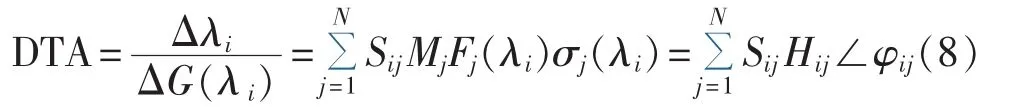
式（8）表明，UPFC稳定器向目标模态的阻尼传递过程可分为2个阶段：先是稳定器向各发电机组提供阻尼转矩；再是各机组对目标模式的参与程度。

DTA表征了模态Δλi对稳定器ΔG（s）的灵敏度,其值越大表明阻尼控制器对模态提供的阻尼越多，因此可通过DTA指标选择UPFC最佳阻尼通道。理论上DTA是一个复数，表示为幅值、相位的组合。下文中稳定器参数设计采用相位补偿法，理想条件下相位得到完全补偿。假设DTA=KDTA∠φ，类比于PSS相位补偿法，稳定器传递函数理想设计为G（s）=Kp∠（-φ），相位信息主要决定阻尼控制器的时间常数，因此DTA幅值信息亦可作为判别指标。

3 UPFC多个稳定器的协调设计

由DTA分析结果可知，稳定器向全体发电机均提供阻尼。为简化计算，本节中，每个模态下只考虑参与因子最大的发电机，定义为模态主发电机。

UPFC附加稳定器后，全系统闭环线性化方程可表示为：

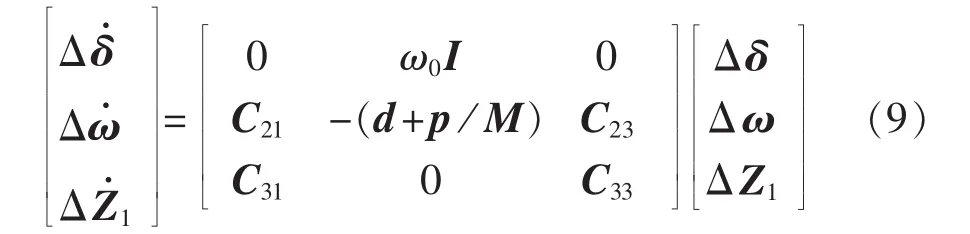
其中，d为发电机固有阻尼系数与转子惯性常数的比值；p为稳定器向主发电机的机电振荡回路提供的等效阻尼系数；Z1为系统其他状态变量向量（包括UPFC及其附加稳定器的状态变量）。

本节提出的协调设计整体思路如下。

a.选定目标模态，利用参与因子确定每个模态的主发电机。

b.构造无约束优化问题，目标函数为：

其中，p=［D1，D2，…，DN］；λi为系统中第i个优化模态；为第i个模态的理想整定值；N为主发电机台数，N≤n。整定多模态时，若，则 f（p）≈0，表明结果达到优化目标。

c.利用 Hooke-Jeeves直接搜索法［14］求解上述无约束优化问题，计算得到稳定器分别向N台主发电机提供的等效阻尼系数 Di（i=1，2，…，N）。该算法具有很强的局部搜索能力，收敛速度快，精度高。虽然其优化结果比较依赖于初值的选取，但是本文主要研究小干扰稳定性，阻尼模态前后变化幅度不是很大，因此初值问题可不予考虑。

d.依据DTA指标选取UPFC阻尼通道，采用相位补偿法分别设计每个稳定器的参数。

图3 协调设计算法流程图Fig.3 Flowchart of coordinated design

UPFC多个稳定器参数的协调优化算法整体流程如图3所示。图3中，α为计算步长；β为加速因子；ε 为收敛精度；e（k）=（0，…，0，1，0，…，0）T，k=1，2，…，N表示N个坐标轴方向（N台主发电机对应有N个坐标轴方向）。

4 算例分析

4.1 UPFC最佳阻尼通道选取

装设UPFC的四机两区域系统如图4所示。经特征值分析，可得该系统存在3个模态：λ1=-0.15+j5.77，λ2=-0.16+j6.01，λ3=-0.06+j2.92。本节对区域振荡模态 λ3（G1G2-G3G4，即发电机 G1、G2与发电机G3、G4对振）选取UPFC最佳阻尼通道。四机系统UPFC附加阻尼控制的DTA指标计算结果见表1。

图4 装设UPFC的四机系统Fig.4 Four-machine power system with UPFC

表1 UPFC的DTA指标Table 1 Values of UPFC DTA index

通过比较表1中DTA指标大小可发现，4个阻尼通道的优先级应依次为me-UE、δe-Udc、mb-Q、δb-P；me-UE为UPFC的最佳阻尼通道，该通道安装稳定器在四机系统中的阻尼传递框图如图5所示。

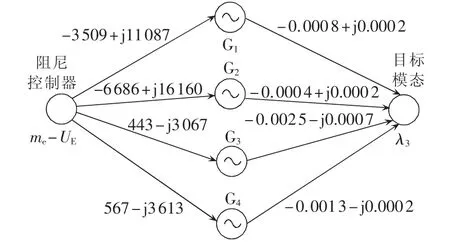
图5 UPFC阻尼分配图Fig.5 Diagram of UPFC damping assignment

非线性仿真结果如图6所示（δG1-G3为G1与G3之间的功角差），系统运行0.1 s时节点8处发生三相短路故障，0.2 s时故障清除。从图6中结果可知，me-UE通道附加阻尼效果最为明显，4个通道附加阻尼效果优先级顺序依次为me-UE、δe-Udc、mb-Q、δb-P，与DTA计算结果相一致，可见DTA指标能够有效选择UPFC的最佳阻尼通道。

图6 阻尼通道对比仿真结果Fig.6 Comparison of simulative result among damping channels

4.2 UPFC多个稳定器协调设计

装设UPFC的IEEE 9节点标准算例系统如图7所示。特征值和DTA计算结果见表2。

图7 装设UPFC的IEEE 9节点系统Fig.7 IEEE 9-bus system with UPFC

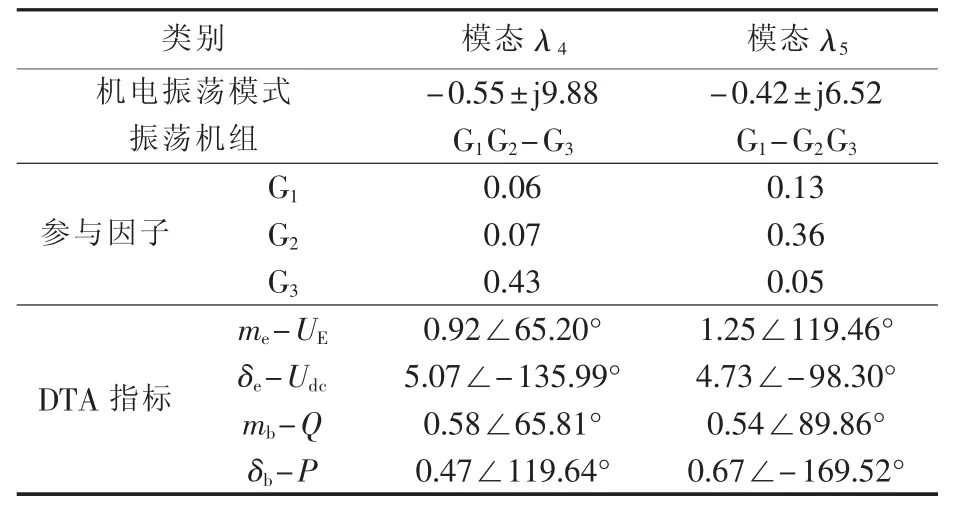
表2 特征值和DTA计算结果Table 2 Eigenvalues and calculated values of DTA index

由表2可知，针对模态λ4，G3的参与因子最大，确定为主发电机；针对模态λ5，G2的参与因子最大，确定为主发电机。依据DTA指标，优先级较高的阻尼通道为me-UE和δe-Udc。因此，选择me-UE通道装设稳定器抑制模态λ4，δe-Udc通道装设稳定器抑制振荡模态λ5。

通过装设2个稳定器，将2个目标振荡模态分别整定到（2个模态的阻尼比均提高至0.1）。表3给出了通过直接寻优法得到的主发电机阻尼系数，以及应用相位补偿法设计的控制器参数，直接寻优法的寻优过程如图8所示。

非线性仿真结果如图9和图10所示（δG1-G2为G1与G2之间的功角差），系统运行0.5 s时节点5处发生三相短路故障，0.6 s时故障清除。从仿真结果可知，当不采取协调设计（即依据DTA指标，将UPFC多通道整合成单向通道，采用相位补偿法设计参数［6，15］）时，图9 中模态 λ4能够得到抑制，但是图10中模态λ5情形发生恶化。依据表2中DTA指标，阻尼通道me-UE和δe-Udc的相位角相差近140°；相位角大于90°的稳定器，若2个稳定器均单一采用相位补偿法独立设计会因相互作用产生负交互影响，恶化稳定器性能［9］；通过本文提出的协调设计方法求得的稳定器参数，图9和图10中的发电机功角振荡均能够得到有效抑制，克服了相位补偿法整定多模态的不足。

表3 协调设计结果统计Table 3 Results of coordinated design

图8 Hooke-Jeeves算法的寻优过程Fig.8 Optimization process of Hooke-Jeeves method

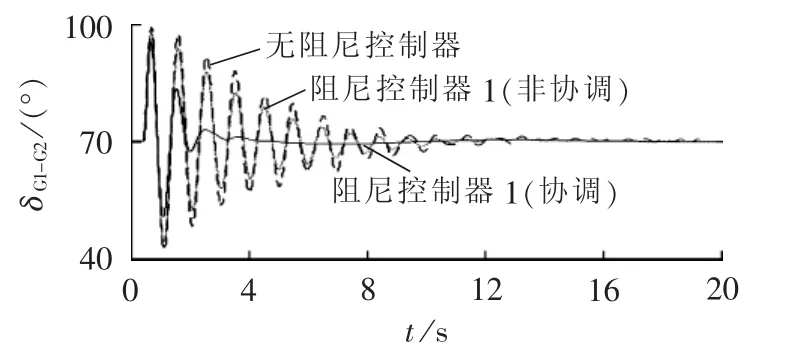
图9 发电机G1与G2功角差仿真曲线Fig.9 Simulative waveforms of generator angle difference between G1and G2

图10 发电机G1与G3功角差仿真曲线Fig.10 Simulative waveforms of generator angle difference between G1and G3

下面通过对功角振荡曲线的Prony分析［16-17］辅证上述结论，为简化说明，分析结果各自筛选出幅值较大的3组数据，详见表4。

由表4可知，对于图9中的功角差曲线，协调设计与非协调设计均提高了阻尼比，其中协调设计的改善效果更为明显；对于图10中的功角差曲线，协调设计结果提高了阻尼比，但是非协调设计的结果恶化了阻尼比。

表4 发电机功角差曲线的Prony分析结果Table 4 Prony analysis of generator angle difference

4.3 区间模态与区内模态协调整定

在UPFC的me-UE和δe-Udc阻尼通道上附加稳定器，协调整定四机系统中模态λ2（G3-G4，即发电机G3与G4对振）和λ3。优化设计参数见表5。

表5 协调设计结果统计Table 5 Results of coordinated design

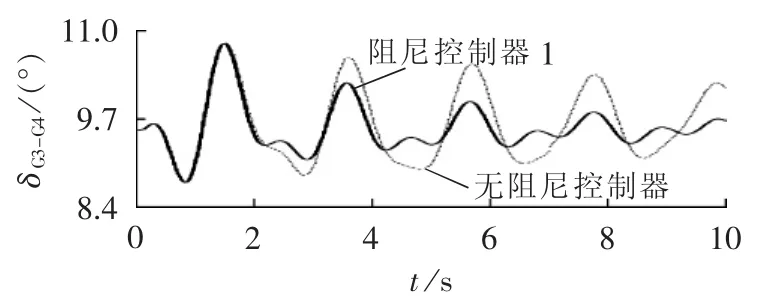
图11 发电机G3与G4功角差仿真曲线Fig.11 Simulative waveforms of generator angle difference between G3and G4

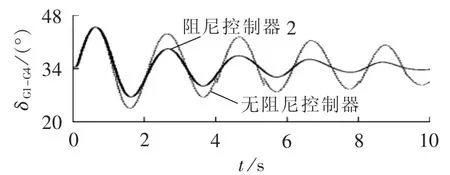
图12 发电机G1与G4功角差仿真曲线Fig.12 Simulative waveforms of generator angle difference between G1and G4

非线性仿真结果如图11和图12所示（δG3-G4、δG1-G4分别为G3与G4、G1与G4之间的功角差），系统设置同4.1节。从仿真结果可知，通过本文提出的协调设计方法求得的稳定器参数，区间振荡模式和区内振荡模式均能够得到有效抑制。

4.4 应用DTA指标比较UPFC附加稳定器与发电机PSS的阻尼效果

针对4.3节的区间与区内两模态，通过DTA指标比较UPFC附加稳定器与发电机PSS［13］的阻尼效果，DTA幅值计算结果详见表6。UPFC稳定器输入信号通常取线路功率信号Pline，而发电机PSS输入信号通常取本地发电机转速信号ωj。为综合比较，表6中UPFC取了本地功率信号和远端发电机转速信号（同PSS输入信号）。

由表6中DTA指标计算结果可知，UPFC附加稳定器选择远端发电机转速信号作为稳定器输入信号时，其阻尼效果不如发电机PSS；若UPFC附加稳定器选取本地线路功率信号作为反馈信号时，其阻尼效果区强于PSS；UPFC主要安装在系统主联络线位置，相比于阻尼区内模态λ2，UPFC附加稳定器阻尼区间模态λ3的效果尤为明显。

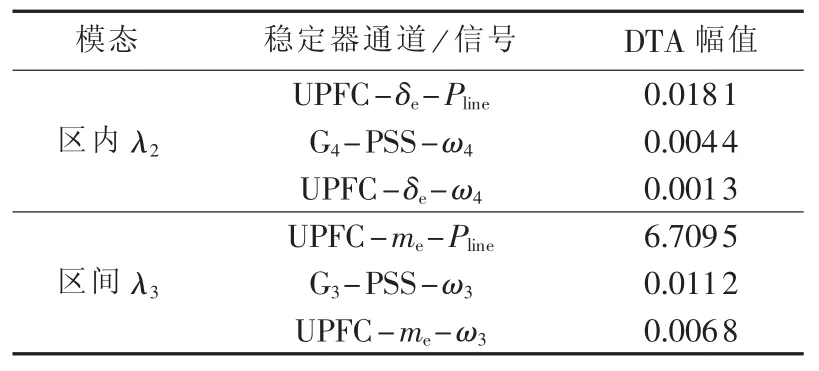
表6 2类稳定器的DTA指标Table 6 Values of DTA index for two stabilizers

5 结论

本文在关于UPFC提高系统低频振荡稳定机理研究的基础上，将DTA方法扩展至包含UPFC的多机电力系统，提出了基于DTA的UPFC最佳阻尼通道选取方法；针对UPFC多个控制回路附加稳定器可阻尼多个低频振荡模态，结合DTA指标优选UPFC多个阻尼通道，提出一种UPFC多个稳定器的协调设计方法，得出如下结论。

a.基于DTA指标能够有效判定UPFC阻尼通道的优先级，能够有效指导稳定器的安装设计。

b.相位补偿法设计的多稳定器之间易发生负交互影响，本文所提出的UPFC多稳定器协调设计方法能够有效克服相位补偿法整定多模态的不足。

c.UPFC安装多个稳定器抑制低频振荡，能够同时兼顾区间振荡模式和区内振荡模式。UPFC通常安装在系统主联络线位置，相比发电机PSS，UPFC附加稳定器阻尼区间振荡效果更为显著，具有更广阔的适用范围和应用前景。

基于DTA计算结果，UPFC的4个阻尼通道中只有me-UE和δe-Udc通道附加稳定器效果明显。大型电力系统中的低频振荡情况复杂，往往一个模态由多台发电机组共同参与，可能需要稳定器与发电机PSS的协调优化［12］。因此，下一步研究重点是基于本文提出的协调设计思路进行UPFC稳定器与发电机PSS的协调优化整定。

参考文献：

［1］祁万春，杨林，宋鹏程，等.南京西环网UPFC示范工程系统级控制策略研究［J］.电网技术，2016，40（1）：92-96.QI Wanchun，YANG Lin，SONG Pengcheng，et al.UPFC system control strategy research in Nanjing western power grid［J］.Power System Technology，2016，40（1）：92-96.

［2］WANG H F，SWIFT F J.A unified model for the analysis of FACTS devices in damping power system oscillations.I.singlemachine infinite-bus power systems［J］.IEEE Transactions on Power Delivery，1997，12（2）：941-946.

［3］WANG H F，SWIFT F J，LI M.A unified model for the analysis of FACTS devices in damping power system oscillations.Ⅱ.multimachine power systems［J］.IEEE Transactions on Power Delivery，1998，13（4）：1355-1362.

［4］WANG H F.Applications of modelling UPFC into multi-machine power systems［J］.IEE Proceedings-Generation，Transmission and Distribution，1999，146（3）：306-312.

［5］WANG H F.A unified model for the analysis of FACTS devices in damping power system oscillations.Ⅲ.unified power flow controller［J］.IEEE Transactions on Power Delivery，2000，15（3）：978-983.

［6］陈中，杜文娟，王海风，等.基于阻尼转矩分析法的储能系统抑制系统低频振荡［J］.电力系统自动化，2009，33（12）：8-11.CHEN Zhong，DU Wenjuan，WANG Haifeng，et al.Power system low-frequency oscillations suppression with energy storage system based on DTA［J］.Automation of Electric Power Systems，2009，33（12）：8-11.

［7］史林军，张磊，陈少哺，等.飞轮储能系统在抑制电力系统多模式振荡中的应用［J］.东南大学学报（自然科学版），2012，42（2）：323-327.SHI Linjun，ZHANG Lei，CHEN Shaobu，et al.Power system lowfrequency oscillations suppression with energy storage system based on DTA［J］.Journal of Southeast University（Natural Science Edition），2012，42（2）：323-327.

［8］蒋平，栗楠，顾伟，等.PSS和SVC联合抑制特高压网络低频振荡［J］.电力自动化设备，2009，29（7）：13-16.JIANG Ping，LI Nan，GU Wei，et al.Restraining low frequency oscillation of UHV power grid using PSS and SVC［J］.Electric Power Automation Equipment，2009，29（7）：13-16.

［9］WANG H F.Design of non-negatively interactive FACTS-based stabilizers in multi-machine power systems［J］.Electric Power Systems Research，1999，50（3）：169-174.

［10］赵登福，孙瑜，孟岩，等.复杂电力系统多方式下低频振荡抑制器优化配置的研究［J］.中国电机工程学报，2006，26（增刊 1）：27-30.ZHAO Dengfu，SUN Yu，MENG Yan，et al.Optimal allocation of oscillation-damping devices for complex power system considering multiple operating conditions［J］.Proceedings of the CSEE，2006，26（Supplement 1）：27-30.

［11］胡晓波，杨利民，陈中，等.基于人工鱼群算法的PSS参数优化［J］.电力自动化设备，2009，29（2）：47-50.HU Xiaobo，YANG Limin，CHEN Zhong，et al.PSS parameter optimization based on artificial fish-swarm algorithm［J］.Electric Power Automation Equipment，2009，29（2）：47-50.

［12］史林军，张磊，陈少哺，等.多机系统中飞轮储能系统稳定器与PSS 的协调优化［J］.中国电机工程学报，2011，31（28）：1-8.SHI Linjun，ZHANG Lei，CHEN Shaobu，et al.Coordination and optimization of FESS-based stabilizers and PSS in multi-machine power systems［J］.Proceedings of the CSEE，2011，31（28）：1-8.

［13］陈中.阻尼转矩分析法在大规模区域互联电力系统中的应用研究［J］.电力系统保护与控制，2011，39（12）：102-105.CHEN Zhong.Study of the DTA application in large scale interconnected power system［J］.Power System Protection and Control，2011，39（12）：102-105.

［14］HOOKE R，JEEVES T A.Direct search solution of numerical and statistical problems［J］.Journal of ACM，1961，8（22）：212-229.

［15］杜文娟，王海风.电力系统低频功率振荡阻尼转矩分析分析理论与方法［M］.北京：科学出版社，2015：40-45.

［16］竺炜，唐颖杰，周有庆，等.基于改进Prony算法的电力系统低频振荡模式识别［J］.电网技术，2009，33（5）：44-47.ZHU Wei，TANG Yingjie，ZHOU Youqing，et al.Identification of power system low frequency oscillation mode based on improved Prony algorithm［J］.Power System Technology，2009，33（5）：44-47.

［17］王家林，夏立，吴正国，等.采用改进Prony算法的电力系统故障暂态信号分析［J］.电力自动化设备，2012，32（7）：89-93.WANG Jialin，XIA Li，WU Zhengguo，et al.Analysis of power system transient signal based on improved Prony algorithm ［J］.Electric Power Automation Equipment，2012，32（7）：89-93.