新型三相PWM整流器无交流电压传感器控制方法
卢子广 ,林 远 ,胡立坤 ,2,黄太昱 ,2,张文元
(1.广西大学 电气工程学院,广西 南宁 530004;2.广西电力系统最优化与节能技术重点实验室,广西 南宁 530004)
0 引言
在广泛采用的三相电压型脉冲宽度调制(PWM)整流器控制系统中,一般需要3种传感器,分别用来检测直流母线电压、逆变器输出交流电流、电网电压。众多传感器的存在会使得系统结构变得复杂,同时造成高额硬件成本。在实际控制系统中,直流母线电压传感器用于控制外环电压,从而稳定直流侧电压、提供过压保护信号,交流电流传感器用于反馈电流内环、提供过流保护信号,两者均难以省去[1]。因此,关于无交流电压传感器的方法研究较多[2-9]。
文献[2]直接利用整流器的电压方程对电压进行估算,由于电压方程中包含电流的微分量,这很容易产生高频信号,同时放大噪声干扰。因此,为了避免对电流的微分运算,现有较多的无电网电压传感器技术采用虚拟磁链定向的方法[3-9]。其将整流器的交流侧等效为一个虚拟电动机,电网电压可以看作是虚拟磁链的微分,通过对电网电压的积分可以得到虚拟磁链,但在实际应用中需要解决积分初值、积分饱和与直流偏移问题。文献[3]提出带饱和限幅反馈环节的积分器代替纯积分,解决积分饱和问题。文献[4-10]均采用低通滤波器代替纯积分对虚拟磁链进行估计,抑制积分饱和与直流偏移,其中文献[6]提出带初值估计的虚拟磁链观测器估算磁链,通过低通滤波器代替纯积分,能够增强系统的抗干扰能力,改善系统动态性能,但不可避免地带来相位延迟与幅值误差;文献[7]采用滑模观测器观测电网电压,采用带反馈补偿自适应调节的低通滤波器代替纯积分得到虚拟磁链信号,滤去了高次谐波分量;文献[8-9]采用串联2个低通滤波器对传统低通滤波器进行改进,不同的是文献[9]中忽略电感两端的电压,直接对逆变器侧电压进行积分得到机端虚拟磁链;文献[10]提出在不平衡电网状态下利用二阶广义积分器 SOGI(Second-Order Generalized Integrator)实现频率自适应,并对低通滤波器的信号进行幅值与相位补偿,但运算复杂。实际计算中,虚拟磁链与交流电机估算定子磁链非常相似,需要解决积分初值和积分偏移问题。文献[11-12]提出改进低通滤波器,解决交流电机需要对反电动势进行纯积分运算的问题。上述方法中或解决初值问题,或采用低通滤波器,再对其造成的幅值与相位偏差进行补偿,这都增加了系统的复杂性,且无法从根本上消除积分初值、积分饱和与直流偏移问题。
由于SOGI能够对特定频率的正弦信号进行无静差跟踪并产生同幅值的正交量,因此常被用于构建静止坐标系下的锁频环,尤其是在电网电压畸变的情况下实现频率自适应。文献[13]应用SOGI在两相静止坐标系下实现正负序分离,同时提出双二阶广义积分器锁频环(DSOGI-FLL)锁频。但SOGI无法消除输出电流中存在的直流偏置。在此基础上,文献[14]提出三阶广义积分器 TOGI(Third-Order Generalized Integrator),构造正交信号发生器OSG(Orthogonal Signal Generator),分析其跟踪特定频率正弦信号的特性及抑制输入信号所含直流分量的原理,并实现锁频;文献[15]应用多级的TOGI构造OSG交叉对消电流反馈控制,滤除输入信号中的谐波与直流分量。
本文根据文献[14]提出的TOGI-OSG,能够在基于SOGI构造的正交滤波器的基础上,消除输出电流中存在的直流偏置问题。因此,本文提出应用TOGIOSG重构三相电网电压的方法,进而实现三相PWM整流器的无交流电压传感器控制。理论分析TOGIOSG能够实现电网电压观测的原理及其参数整定过程,研究了一种基于TOGI-OSG的三相PWM整流器无交流电压传感器的控制策略,相比基于虚拟磁链的无交流电压传感器控制,所提方法能有效消除电网电压、整流器输入电流中存在的直流分量。
1 TOGI-OSG的基本原理
图1为TOGI-OSG的结构图。该结构以信号u(t)和该信号的频率值ωn作为输入,输出得到3个信号 u1(t)、u2(t)、u3(t)。特别地,当输入为正弦信号时,通过构造可以得到输入信号的估计值以及该估计值的正交量,同时分析可知该结构相当于对输入信号进行了滤波处理,下文将具体说明。
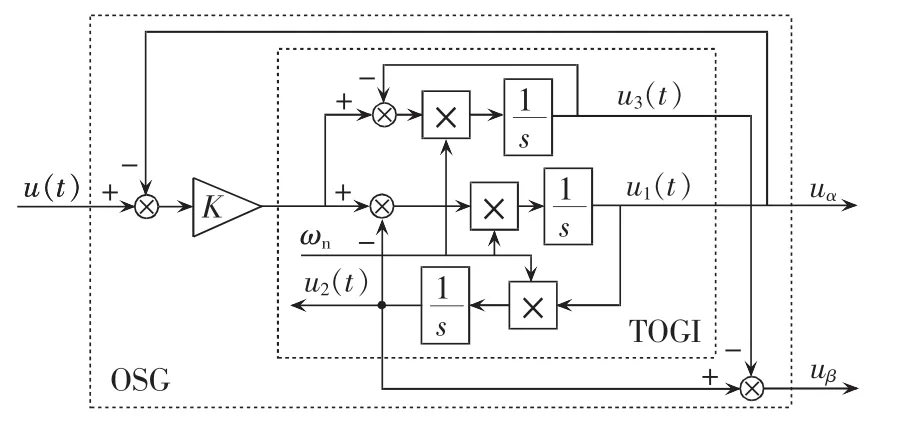
图1 TOGI-OSG结构图Fig.1 Structure of TOGI-OSG
由图1可以得出3个输出信号到输入信号的传递函数分别为:

其中,K 为增益系数;U(s)、U1(s)、U2(s)、U3(s)分别为u(t)、u1(t)、u2(t)、u3(t) 的拉氏变换;F1(s)、F2(s)、F3(s)为闭环传递函数,其 Bode 图如图2、3、4 所示。

图2 K取不同值时 F1(s)的 Bode图Fig.2 Bode diagram of F1(s) for different values of K

图3 K取不同值时 F2(s)的 Bode图Fig.3 Bode diagram of F2(s) for different values of K

图4 K取不同值时 F3(s)的 Bode图Fig.4 Bode diagram of F3(s) for different values of K
由图2、3、4 可以看出:F1(s)实为带通滤波器,而F2(s)实为低通滤波器;增益系数K越大,滤波器的通频带越大,但滤波效果不可避免地变差;而K越小,滤波器的滤波效果越好,但响应速度变慢;在谐振频率 ωn处,F1(s)和 F2(s)始终保持为单位增益,且F1(s)没有相位误差,F2(s)的相位滞后 90°,因此滤波器的两输出信号正交且频率相同;F3(s)实为陷波滤波器,只在频率ωn处的增益无穷小,且无相移。所以TOGI对输出信号有一定的滤波功能,即有一定的谐波抑制能力。因此以TOGI为基础构造OSG,可以抑制直流分量对系统的影响。
假设输入信号为含有直流分量的正弦信号,以此来说明TOGI-OSG及其抑制直流分量的原理。输入信号的表达式如下:
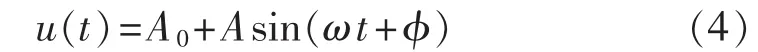
其中,A0为直流偏移量;A为正弦信号幅值;φ为初相位。
如果TOGI的输入频率ωn等于输入信号的频率ω,由文献[14]可知,TOGI的3个输出信号分别为:

其中,u1∞(t)、u2∞(t)、u3∞(t)分别为u1(t)、u2(t)、u3(t)在某个时刻达到稳态后的量。由式(5)—(7)可见:输出信号 u1(t)不包含直流分量,这是因为式(1)分子包含一阶微分项;输出信号u2(t)包含直流分量,其交流分量与输入信号幅值相同,相位滞后90°,这也说明SOGI无法消除输入信号中直流分量对输出交流信号β轴分量的影响;输出信号u3(t)仅含直流量,且与 u2(t)中的直流分量相等。由 u1(t)、u2(t)、u3(t) 的表达式可以得出,u2(t)-u3(t)与 u1(t)正交,即 u2(t)-u3(t)与 u1(t)幅值相同、相位相差 90°,且都不包含直流分量。由此可见,应用TOGI能够构造与输入信号同幅同相的两相正交信号,且能够消除输入信号中包含的直流分量。
2 参数K的整定方法
由图2、3、4可以看出K取值对响应速度和滤波效果的变化趋势,但无法给出精确分析。下面从经典控制理论角度分析参数K的选取。
以输出信号u2(t)为例。根据经典控制理论,为了获得系统所要求的性能,包括响应速度和超调量,需要选择合适的阻尼比,本节选择阻尼比。比较F2(s)与二阶闭环系统标准传递函数(如式(8)所示),可得,因此。
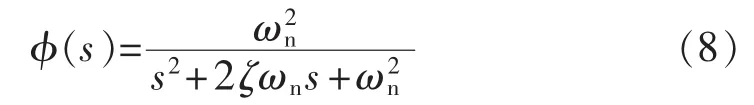
为了具体说明参数选择是否恰当,在MATLAB/Simulink环境中建立TOGI-OSG的仿真模型。对给定的 3 个输入信号 ua=100 sin(314 t)、ub=100×,将其通过坐标变换为两相静止坐标系下的量 uα、uβ,并输入TOGI-OSG,再经过旋转变换得到相应的直流分量ud、uq。通过观察ud的阶跃响应来具体说明K的取值对TOGI-OSG阶跃响应的影响。当K取值为0.1、0.5、0.707、1、1.414、1.6、2、5 时,阶跃响应和输出响应结果分别如图5和图6所示。

图5 K取不同值时TOGI-OSG的阶跃响应Fig.5 Step response of TOGI-OSG for different values of K
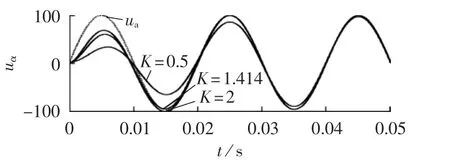
图6 K取不同值时TOGI-OSG的输出响应Fig.6 Output response of TOGI-OSG for different values of K
从图5和图6可以看出,K取值大则响应速度快,但K过大会导致超调严重甚至振荡;K过小则响应速度慢,无法满足控制要求。当K取1.414时能保证较快的响应速度和较小的超调,与理论计算一致。
3 基于TOGI-OSG的三相PWM整流器无交流电压传感器控制策略
3.1 电压估算方法
三相PWM整流器在两相静止坐标系下的数学模型[6]为:
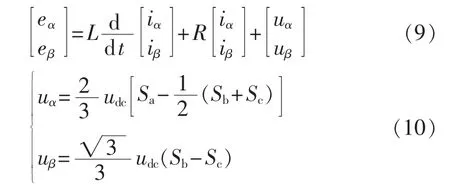
其中,分别为网侧电压和电流的 α、β 轴分量;uα、uβ分别为整流器交流侧三相电压的α、β轴分量;L为滤波电感;R为滤波电感等效电阻;udc为直流侧电压;Sa、Sb、Sc为整流器的开关函数,Sa=Sb=Sc=1表示相应的上桥臂导通、下桥臂关断,Sa=Sb=Sc=0表示相应的下桥臂导通、上桥臂关断。
根据式(9)可直接得到基本的电压观测器模型,但式(9)包含电流的微分量,如果直接根据其估算电压计算将很容易产生高频信号。虚拟磁链的控制方法可以避免对电流直接微分,然而常规的虚拟磁链控制方法存在直流偏移问题。基于SOGI的正交滤波器可以避免对电流的微分运算,降低谐波干扰,但其无法消除输出电流中存在的直流分量。事实上,TOGI-OSG无需微分运算,能较好抑制谐波的干扰,同时能有效消除交流电压、电流中存在的直流分量。
由于电网电压、电流均为正弦信号,而正弦信号的微分量与原信号正交,所以可通过TOGI-OSG得到电流的微分。于是由式(9)可推导得到基于TOGIOSG的电压观测器的数学模型为:

其中,带“^”的变量均为经过TOGI-OSG的估计量;与与相互正交;ωs为电网频率;G1、G2分别为原信号估计与正交信号估计的传递函数;G为电压观测器的传递函数。
因此可以得到电压观测器的结构框图如图7所示。
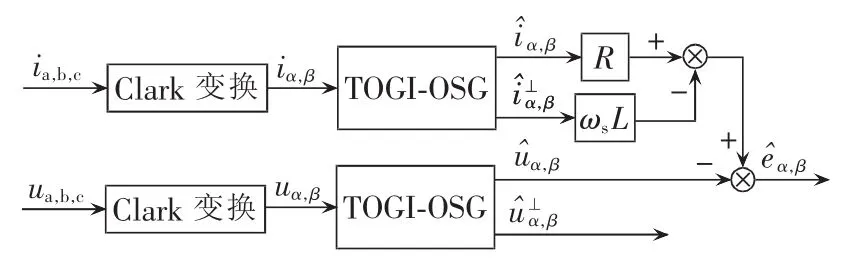
图7 电压观测器结构框图Fig.7 Block diagram of voltage observer
3.2 系统控制结构
本文研究的无交流电压传感器三相PWM整流器控制系统采用直流母线电压、无功功率外环(简称UQ控制),电流内环的控制方法。其中,电网电压由TOGI-OSG估算得到两相静止坐标系下的α、β轴分量,并用于无功功率的计算;直流母线电压环采用比例积分 PI(Proportional Integral)控制器,用于稳定、控制直流母线电压,生成内环有功电流指令值;无功功率环采用PI控制器用于控制无功功率流动,生成内环无功电流指令值;电流环采用比例谐振PR(Proportion Resonant)控制器。基本控制框图见图8。
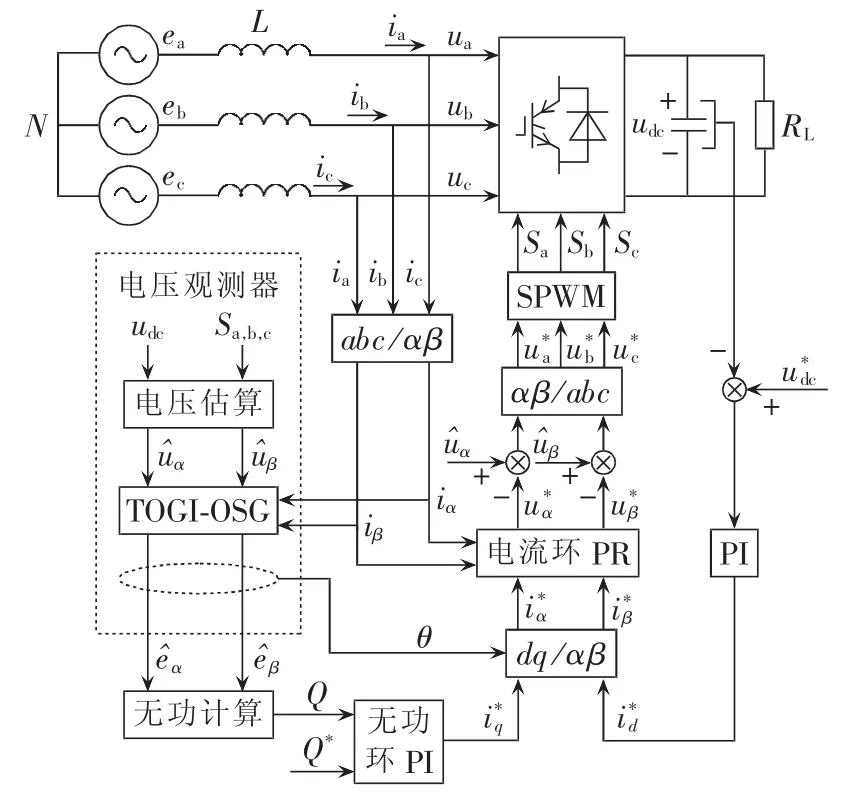
图8 三相PWM整流器控制框图Fig.8 Block diagram of three-phase PWM rectifier control
4 仿真及实验分析
4.1 仿真分析
为了验证所提控制方法的有效性,在MATLAB/Simulink环境下,基于图8的控制框图建立仿真模型。仿真参数为:直流侧电容C=4400 μF,进线电抗器电感L=2 mH,进线电抗器电阻R=0.05 Ω,直流侧电压给定udc=150 V,交流电压观测器参数K=1.414。
对于有电压传感器的并网控制系统,在电网电压与并网电流中叠加直流分量,开环估算电网电压,给出估算电压α轴分量的仿真结果如图9所示。可以看出,纯积分运算无相位滞后,但当存在直流偏移量时,出现积分漂移,无法用于实际控制;低通滤波器能较好地抑制直流偏置,但存在相位与幅值偏差;TOGI-OSG估算的电网电压能够在较短时间后与实际电网电压重合,说明基于TOGI-OSG的观测方法可以很好地解决纯积分存在的问题,快速准确地估计电网电压。

图9 uα的仿真结果Fig.9 Simulative results of uα
为了说明所提方法的有效性,将TOGI-OSG估算的电网电压接入闭环,实现三相PWM整流器无交流电压传感器控制。图10为投切负载的仿真波形。在0.2 s时刻,直流侧接入30 Ω电阻负载,直流母线电压经过短暂波动后迅速恢复,估算电网电压稍有跌落后迅速恢复,由图10(d)可知,输出电流与电网电压同相位。在0.3 s时刻,给定无功功率Q*=-500 var,直流母线电压基本无波动,估算电压稍有变大后迅速稳定。对比图10(a)、(b)可知,在整个过程中,电压观测器均能够准确估计电网电压。由图10(f)可知有功、无功实现准确解耦。从仿真结果可知,基于TOGI-OSG的电压观测器能准确快速地估计电网电压用于实际控制系统,实现无交流电压传感器控制。
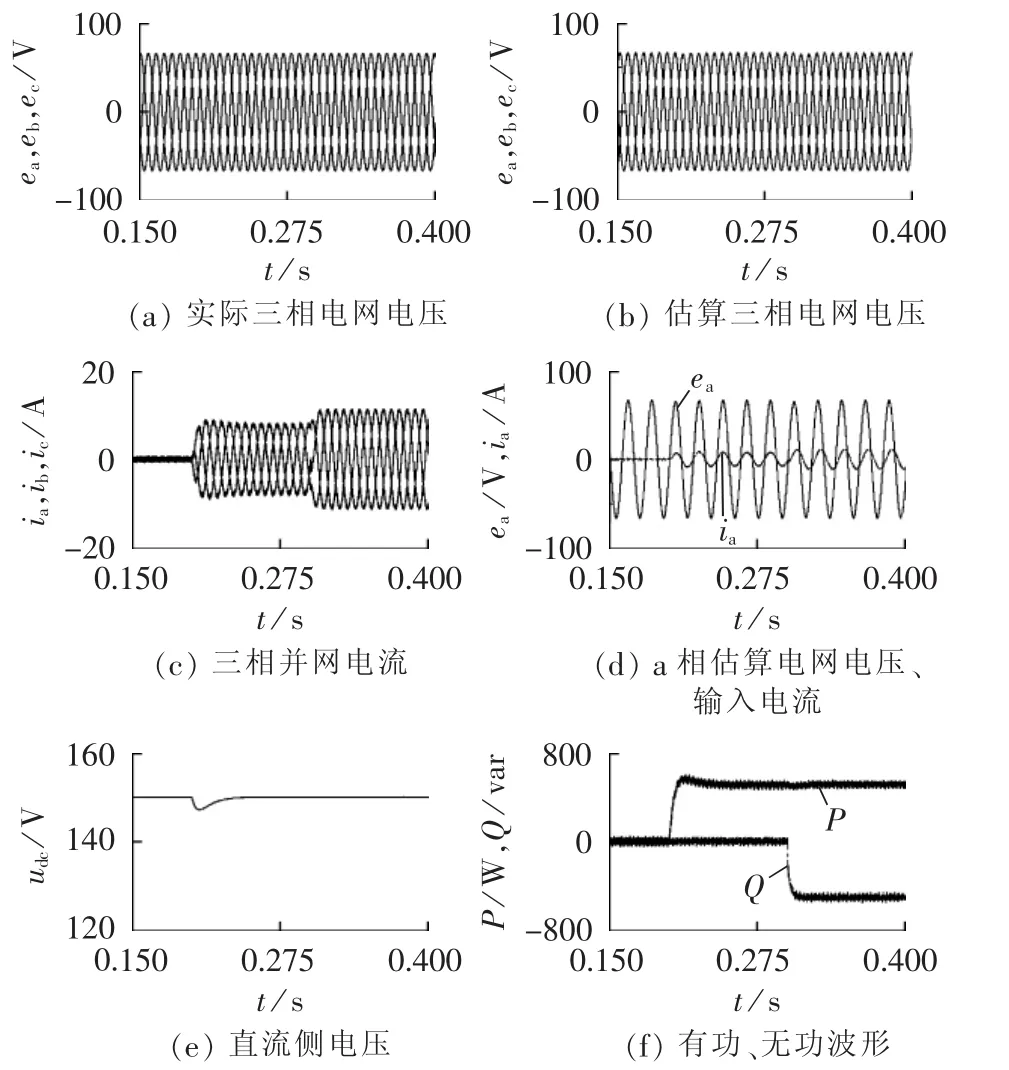
图10 投切负载的仿真结果Fig.10 Simulative results of sudden load changes
为了说明所提方法抑制直流偏置的有效性,将基于虚拟磁链(使用低通滤波器代替纯积分)的无电压传感器控制方法(方法一)与本文所提方法进行对比。在输入电流与电网电压中叠加一定的直流量,保持各控制器参数一致,对比2种控制方法估算的电网电压、直流母线电压与网侧输入电流波形。仿真结果如图11所示。
在0.2 s时刻投入30 Ω电阻负载,由图11(e)、(f)可知2种方法均能使得直流母线电压在短暂下跌后迅速恢复。但基于虚拟磁链无电压传感器控制的电网估算电压偏大,直流母线电压下跌较大,在无负载时,三相并网电流不为0。0.3 s时刻在输入电压中叠加10 V的直流电压、在网侧输入电流中叠加1 A的直流电流,可以看出基于TOGI-OSG的无交流电压传感器控制可以正确估计电网电压,网侧输入电流不受影响,直流母线电压保持稳定;而基于虚拟磁链的无交流电压传感器控制估算的电网电压、网侧输入电流、直流母线电压均出现较大波动。因此,基于TOGI-OSG的无交流电压传感器控制方法不存在直流偏置问题,能够准确地估算电网电压。
4.2 实验结果分析
为了验证本文所提方法的性能,根据图8搭建了以dSPACE平台的DS1104为核心的三相PWM整流电路,实验主电路参数与仿真参数一致。
图12给出了整流器投入负载过程的实验结果(图中,Pv、Qv分别为由估算电压计算的有功、无功功率;Pu、Qu分别为由实际电压计算的有功、无功功率;Pdc为直流侧有功功率),可以看出估算电网电压可以快速收敛到稳态值,估算电压与输入电网电流同相位,直流母线电压能够在投入负载过程中快速地稳定在给定值,三相电流波形正弦度较好。由于实际系统存在能量损耗,由图12(i)可以看出直流侧功率与由估算电网电压计算的有功功率相等;给定无功指令Q*=0,由估算电压计算的无功功率为0,从参与控制的角度来看,无电压传感器控制方法无法将系统的损耗考虑进去,这就导致估算的电网电压在投入负载时发生跌落,但当电压升高、功率等级提升后,系统能量消耗与电压降落可忽略不计。

图12 投入负载实验结果Fig.12 Experimental results of sudden load changes
为了说明所提方法抑制直流偏置的效果,将本文所提方法与基于虚拟磁链的无电压传感器控制方法(传统方法)进行对比实验。由于电网电压、电流的检测不可避免地存在直流分量,在估算整流器侧交流电压叠加5 V的直流电压、输入电网电流中加入0.5 A的直流电流。实验结果如图13所示。
由图13可知,基于TOGI-OSG的无交流电压传感器控制方法可以正确估计电网电压、保持母线电压稳定无波动;而基于虚拟磁链的无电压传感器控制方法中估算电网电压发生偏移、直流电压发生波动。因此,基于TOGI-OSG的电网电压估计方法能有效地消除直流分量的影响,准确估算电网电压。

图13 叠加直流分量的实验结果对比Fig.13 Comparison of experimental results when DC components are superposed
5 结论
所提三相电压型PWM整流器无交流电压传感器控制方法是由TOGI-OSG观测得到电网电压,并将其应用于PWM整流器控制系统中,达到省去交流电压传感器、降低PWM整流器硬件成本的目的;准确估算出电网电压是进行控制的关键,本文分析了应用虚拟磁链、基于SOGI正交滤波器估算电网电压存在的主要问题,在此基础上,应用TOGI-OSG观测电网电压,避免了电流微分与纯积分运算,有效地消除了估算电网电压存在的直流偏置误差问题,同时改善了输入电流波形。由于电压估算过程采用的是固定的电网频率,在下一步研究中可以考虑实现频率自适应以应对电网及负载波动。
参考文献:
[1]MALINOWISKI M,MARIUSZ S C.Sensorless control strategies for three-phase PWM rectifiers[D].Warsaw,Poland:Warsaw University of Technology,2001.
[2]OHNUKI T,MIYASHITA O,LATAIRE P,et al.A three-phase PWM rectifier without voltage sensors[C]∥Proceedings of the European Conference on PowerElectronicsand Applications(EPE).Trondheim,Norway:EPE,1997:881-886.
[3]吴凤江,孙秀冬,孙力,等.无交流电压传感器并网逆变器的控制策略及其改进[J].电力自动化设备,2009,29(7):33-37.WU Fengjiang,SUN Xiudong,SUN Li,et al.Control strategy of grid-connected converterwithoutAC voltage sensorand its improvement[J].Electric Power Automation Equipment,2009,29(7):33-37.
[4]WRONA G,MALON K.Sensorless operation of an active front end converter with LCL filter[C]∥2014 IEEE 23rd International Symposium on Industrial Electronics(ISIE).Santiago,Chile:IEEE,2014:2697-2702.
[5]SUUL J A,LUNA A,RODRIGUEZ P,et al.Virtual-flux-based voltage-sensor-less power control for unbalanced grid conditions[J].IEEE Transactions on Power Electronics,2012,27(9):4071-4087.
[6]赵仁德,贺益康.无电网电压传感器三相PWM整流器虚拟电网磁链定向矢量控制研究[J].中国电机工程学报,2005,25(20):56-61.ZHAO Rende,HE Yikang.Virtual line-flux-linkage oriented vector controlofthree-phasevoltagesource PWM rectifierwithout voltage sensors[J].Proceedings of the CSEE,2005,25(20):56-61.
[7]肖雄,张勇军,王京,等.无电压传感PWM整流器的虚拟磁链自适应滑模观测研究[J].电工技术学报,2015,30(12):152-161.XIAO Xiong,ZHANG Yongjun,WANG Jing,et al.PWM rectifiers based on adaptive sliding-mode observer with virtual flux orientation under non-line voltage sensors control[J].Transactions of China Electrotechnical Society,2015,30(12):152-161.
[8]王晗,窦真兰,张建文,等.基于LCL的风电并网逆变器无传感器控制[J].电工技术学报,2013,28(1):188-194.WANG Han,DOU Zhenlan,ZHANG Jianwen,etal.Studyon voltage sensor-less control for wind grid connection inverter with LCL filter[J].Transactions of China Electrotechnical Society,2013,28(1):188-194.
[9]卢子广,王淼,胡立坤,等.分布式发电并网逆变器的虚拟电机自然坐标控制[J].中国电机工程学报,2014,34(36):6435-6441.LU Ziguang,WANG Miao,HU Likun,et al.Virtual-machine natural coordinate controlofgrid-connected inverters in distributed power systems[J].Proceedings of the CSEE,2014,34(36):6435-6441.
[10]战杰,张彦,刘其辉,等.基于电网虚拟磁链的变速恒频风力发电机柔性并网技术[J].电力自动化设备,2009,29(12):74-78.ZHAN Jie,ZHANG Yan,LIU Qihui,et al.Flexible grid-connection technology based on virtual flux linkage for VSCF wind generator[J].Electric Power Automation Equipment,2009,29(12):74-78.
[11]OHTANI T,TAKADA N,TANAKA K.Vector control of induction motor without shaft encoder[J].IEEE Transactions on Industry Applications,1992,28(1):157-164.
[12]李彪,李黎川.基于同步旋转坐标系下矢量旋转的新型磁链算法[J].中国电机工程学报,2016,36(5):1421-1429.LI Biao,LI Lichuan.New flux estimation algorithms based on vector rotation under synchronously rotating reference frame[J].Proceedings of the CSEE,2016,36(5):1421-1429.
[13]RODRIGUEZP,LUNA A,MUNOZ-AGUILAR RS,etal.A stationary reference frame grid synchronization system for threephase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics,2012,27(1):99-112.
[14]FEDELE G,FERRISE A,MURACA P.An adaptive quasi-notch filter for a biased sinusoidal signal estimation[C]∥9th IEEE International Conference on Control and Automation (ICCA).Santiago,Chile:IEEE,2011:1060-1065.
[15]黄媛,罗安,陈燕东,等.一种三阶广义积分交叉对消电流反馈控制的多逆变器并联控制策略[J].中国电机工程学报,2014,34(28):4855-4864.HUANG Yuan,LUO An,CHEN Yandong,et al.A current feed-
(continued on page 47)(continued from page 33)back control strategy for parallel operation of multi-inverters using third-order general-integrator crossover cancellation method[J].Proceedings of the CSEE,2014,34(28):4855-4864.

