限幅环节对DFIG故障中输出特性的影响研究
薛安成 ,耿继瑜 ,2,刘瑞煌 ,3,赵成爽 ,王 清 ,毕天姝
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.国网上海市电力公司松江供电公司,上海 201600;3.国网江苏省电力公司电力科学研究院,江苏 南京 211100;4.国网江苏省电力公司苏州供电公司,江苏 苏州 215000)
0 引言
近年来,我国风电产业增长势头强劲,其中双馈感应电机 DFIG(Doubly-Fed Induction Generator)在风电场中得到了广泛应用[1]。大规模DFIG风电机组接入系统,改变了电力系统的结构,给电网安全稳定运行带来了新的挑战[2-5]。因此,准确认识风电机组动态特性成为当前研究的热点之一。
另一方面,在风机控制中,存在广泛的限幅环节[6-7],如空气动力模块中有桨距角限幅,发电机部分有电压、电流限幅和有功功率、无功功率限幅,变流器中包含着PI控制器以及调制器件的限幅等。限幅不仅代表着实际物理设备的能力限制,也体现了控制系统一些特定的考虑因素。限幅是模型中不可缺少的重要部分,对限制系统过电流、过电压及保证风电机组安全稳定运行有重要作用。
然而,值得注意的是,现有的DFIG风电机组动态特性研究主要是对故障后电磁暂态和机电暂态特性的研究[8-11],且主要集中在不同控制策略对其特性的影响上[12-14]。
虽然限幅环节广泛存在于风机系统模型中,但仅有少数文献涉及限幅模型对于风电系统特性的影响。文献[15]探讨了风机中变流器限幅和桨距角限幅导致系统出现切换死区的机理及对动态特性的影响。文献[16]分析DFIG等值模型时初步涉及了限幅模块,但未讨论其影响。文献[17]研究了不对称电压跌落下DFIG风电机组的无功约束过程。文献[18]比较了有无限幅环节对直流电压的影响。总体上,目前在限幅环节对风电系统特性影响方面的研究较少,还不够充分。
本文主要研究限幅环节对DFIG风电机组故障特性的影响,着重分析其对DFIG故障中稳态有功输出特性的影响。
1 故障中稳态的有功输出特性
应用DIgSILENT软件,仿真搭建了某地区实际风电场结构如图1所示。
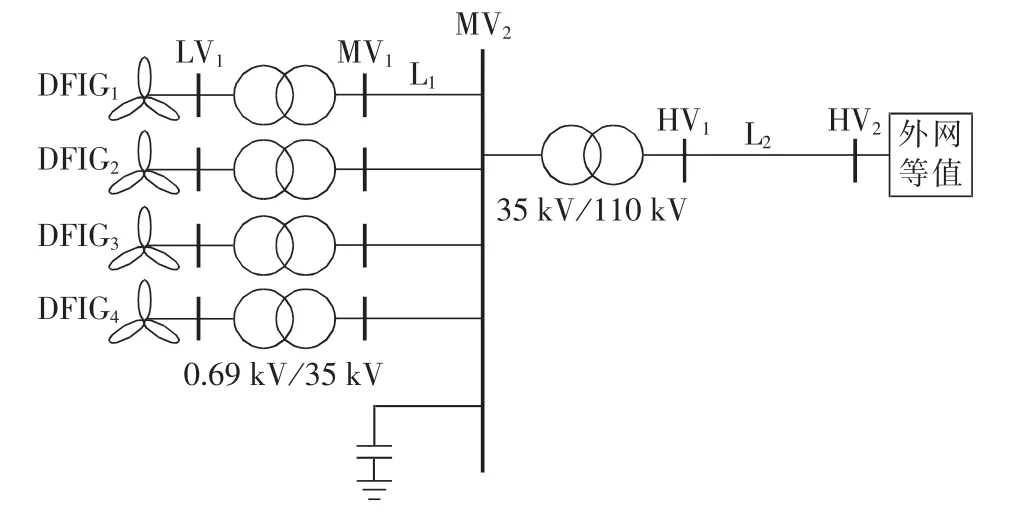
图1 某外送风电场结构图Fig.1 Structure of a wind generation system
风电场相关参数如下:风电机组,DFIG1、DFIG2、DFIG3为 16×1.5 MW 风机,DFIG4为 18×1.5 MW 风机,定子漏抗为0.167 p.u.,转子漏抗为0.1323 p.u.,励磁电抗为5.419 p.u.,定子电阻为0.0084 p.u.,转子电阻为0.0083 p.u.;箱式变压器,容量为1600 kV·A,变比为0.69/35±2×2.5%,阻抗为6.5%,空载电流为0.6%,空载损耗为1.69 kW,负载损耗为16.67 kW;35 kV集电线(L1),平均长度为4.25 km,阻抗为 0.17+j0.365 Ω/km;升压站主变压器,容量为 120 MV·A,变比为 35/110±8×1.25%,阻抗为 10.6%,空载电流为0.1%,空载损耗为65.5kW,负载损耗为359.2 kW;110kV送出线(L2),长度为17.55km,阻抗为0.07232+j0.396 Ω/km;110 kV母线正序等值阻抗,最大运行方式下为0.01385+j0.08409 p.u.,最小运行方式下为0.01511+j0.16978 p.u.。
假设1.0 s时在MV1处发生经电阻的三相对称接地故障,1.5 s时故障切除。考虑不同接地电阻R,可得故障情况下机端电压和有功输出(均为标幺值)变化分别如图2和图3所示。

图2 不同接地电阻下DFIG1机端电压的变化情况Fig.2 Terminal voltage of DFIG1under different grounding resistances

图3 不同接地电阻下DFIG1的有功输出Fig.3 Active power output of DFIG1under different grounding resistances
图2和图3表明,故障期间,机端电压U和有功输出P在经历一个暂态过程后分别达到稳定值U0和P0,其数值基本保持不变,且该机端电压稳态值和有功输出稳态值随着接地电阻值的减小(故障程度加重)而降低。
因此,通过设置不同接地电阻来控制故障中DFIG的机端电压。当接地电阻值较大时,故障中DFIG机端电压较高,此时转子变流器电流较小,Crowbar装置不会触发;当接地电阻值较小时,故障中DFIG机端电压较低,转子变流器上流过的电流超过阈值,将会触发Crowbar装置。Crowbar装置动作后,DFIG的控制系统被屏蔽,此时DFIG输出特性将不再受限幅环节影响,以类异步机模式运行,其模型可等效为一台异步机。因此调节本文中的接地电阻值,控制转子变流器电流始终未达到Crowbar装置的动作限值,Crowbar装置不动作。在此前提下,通过改变接地电阻值,获得不同严重程度的故障中稳态有功输出与稳态电压(均为标幺值)关系,如图4所示。
图4表明,不触发Crowbar动作时,故障中稳态有功输出P0与稳态电压U0关系存在2个拐点,分别在故障中稳态电压为0.7988 p.u.和0.57 p.u.处。当U0≥0.7988 p.u.,即故障较轻时,P0与故障前相同;当 0.57p.u.<U0<0.7988 p.u.时,P0与 U0呈近似线性关系;当U0≤0.57 p.u.时,P0与U0同样呈近似线性的关系,但此时的线性系数与前段的线性系数不同。下文重点分析图4曲线具有上述近似三段折线关系的机理。

图4 故障中稳态有功输出与稳态电压关系Fig.4 Relationship between steady-state active power output and steady-state voltage during fault
2 功率控制模块中的限幅环节
上文分析表明,故障中稳态有功输出和稳态机端电压近似呈三段折线关系,该现象与限幅环节有关。DFIG的控制中包含诸多限幅,鉴于其功率输出特性主要由功率控制模块决定,故本文主要研究功率控制模块中的限幅环节对DFIG暂态特性的影响,即有功功率限幅和转子电流限幅环节。
2.1 有功功率限幅环节
DFIG有功控制模块有多种数学模型,在IEC 61400-27-1[19]中,其等效模型如图5 所示。

图5 IEC标准中DFIG有功控制模块Fig.5 Active power control module of DFIG in IEC standard
图5中,有功功率的限幅包括2个方面:一个是有功功率变化率dPmax的限制;另一个是有功功率幅值PmaxP的限制。其中有功功率变化率dPmax的限制又称作功率恢复缓变率,为一固定值。有功功率幅值PmaxP为机端电压UWT(t)和有功电流最大值ipmax的乘积,其中 ipmax为固定参数,其典型值为 1.47p.u.[2],故有:

其输入与输出的数学描述可写为:

其中,Pref1为输入变量;Pref2为输出变量,与实际有功输出保持一致;x为状态变量,由实际系统决定;dPmax=99 p.u./s为固定参数,下同。
进一步,为考虑控制装置死区等外在因素的限制,DIgSILENT软件采用图6所示模型描述功率控制模块中有功功率的限幅过程。

图6 DIgSILENT中DFIG有功控制模块Fig.6 Active power control module of DFIG in DIgSILENT
其数学描述如下:

其中,λ为中间变量;ipmax取值为1.46154 p.u.(与上文1.47 p.u.接近);ΔP为功率偏移量,取值为0.16923 p.u.。
从安全裕度考虑,有功功率最大限幅值PmaxP限定在 0~1.1 之间,当 UWT(t)≥0.8684 p.u.时,PmaxP=1.1;当 0.1158 p.u.<UWT(t)<0.8684 p.u.时,PmaxP与 UWT(t)呈线性关系,此时曲线的斜率与IEC模型算法中有功限幅曲线的斜率基本一致;当UWT(t)≤0.115 8 p.u.时,PmaxP=0。后续讨论中采用DIgSILENT模型中的有功限幅算法。
2.2 转子电流限幅环节
对于DFIG,在电网电压定向的矢量控制下,忽略定子电阻Rs的影响,可得DFIG定子输出有功功率如下:

其中,Lm为励磁电感;Ls为定子自感;ird为转子电流d轴分量。
进一步,风电机组向电网输出的有功功率如下:

其中,s为运行转差。式(11)表明,当转速基本不变时,风电机组向电网输出的有功功率Pg与转子电流d轴分量ird和机端电压UWT的乘积近似呈正比。
由于故障时间较短,故障期间转速可视为恒定值,即s为一常数。故障过程中,DFIG机端电压降低,转子电流增大,可能达到其极限幅值,此时转子电流的d轴分量ird也达到极限值。当转子电流限幅起作用时,风电机组向电网输出的有功功率如下:
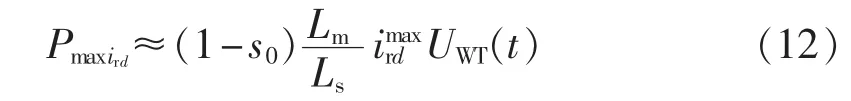
其中,为转子电流限幅下DFIG所能达到的最大有功输出;s0为稳态的转差率。显然,同一机端电压下,转子电流d轴分量的极限幅值取值越大,有功功率的极限值越大。
3 限幅对故障中输出动态特性的影响
利用DIgSILENT软件仿真分析限幅环节对系统故障中动态输出功率的影响。仿真采用图1所示等效模型系统,考虑系统在MV1处发生三相经电阻R的接地故障。Crowbar装置设定如下:若转子电流超过1.47 p.u.,则触发Crowbar投入0.03 s。对比分析考虑/不考虑有功功率限幅和转子电流限幅对DFIG功率输出特性的影响。仿真中考虑如下4种模型:模型①,无限幅环节作用;模型②,仅存在有功功率限幅;模型③,仅存在转子电流限幅;模型④,有功功率与转子电流限幅同时存在。
考虑上述4种模型,可得在接地电阻R=2.4 Ω故障下动态无功和有功功率输出分别见图7和图8。

图7 限幅环节对无功输出的影响Fig.7 Impact of limiter on reactive power output

图8 限幅环节对有功输出的影响Fig.8 Impact of limiter on active power output
图7和图8表明,故障期间,模型①中,无功输出和有功输出均出现大幅振荡,振荡频率与Crowbar装置的投切频率一致。这是因为故障期间无限幅作用时转子电流超过Crowbar装置整定值,造成Crowbar装置频繁投切,使得DFIG不断在感应电机和异步电机间频繁切换。这导致了模型①中风电机组从系统吸收大量无功功率,且无功功率不断波动。在模型②和③中,限幅作用有效减少了故障期间的转子电流,Crowbar装置的投切次数减少。模型④因同时存在有功功率限幅与转子电流限幅环节,转子电流受到双重限制未达到Crowbar装置的动作限值,Crowbar装置不动作。即采用限幅环节可减少模型中Crowbar装置的投切次数。
图7表明,从无功角度看,模型②和③中,系统在故障发生初期会吸收较多无功功率,故障中的稳态时期,无功功率为0;模型④中,故障期间的无功功率几乎为0,与故障前保持一致。因此,模型中采用限幅环节可抑制故障中稳态无功的吸收和波动。
图8表明,从有功角度看,模型②和③中,系统在故障发生初期有功输出呈现一定的波动,故障中的稳态时期波动较小;模型④中,有功输出波动幅度非常小。因此,模型中采用限幅环节可有效抑制故障中稳态有功输出的波动。
上述对比分析表明,在模型中引入限幅环节,可在故障中有效减少Crowbar装置的投切次数,减少风电机组吸收的无功功率,同时抑制功率输出的波动。
4 故障中稳态有功输出的决定因素分析
下面重点研究限幅环节对故障中稳态有功输出特性的影响。
考虑限幅环节影响,由式(8)和(9)可得有功功率限幅下最大有功输出PmaxP和故障严重程度(电压跌落)的关系曲线,如图9中点划线所示;同样,由式(12)可获得转子电流限幅下最大有功输出Pmaxird和故障严重程度(电压跌落)的关系曲线,如图9中点线所示。进一步,考虑系统额定有功输出Pref1的限制,可得到包括有功功率限幅、转子电流限幅、额定有功输出限制(见图9中双点划线)的限幅包络线,由图9中a、b、c段曲线组成。同时,由第1节仿真可获得不同故障严重程度(电压跌落)下DFIG的稳态有功输出,如图9中实线所示。
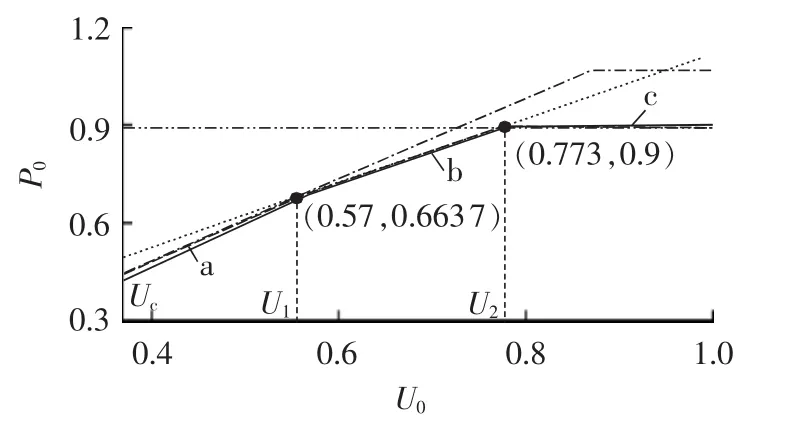
图9 故障中稳态有功输出与稳态电压关系特性Fig.9 Relationship between steady-state active power output and steady-state voltage during fault
图9表明,在满足Crowbar不投入的情形下,故障稳态时期仿真获得的实际有功输出曲线与经有功限幅PmaxP、转子电流限幅Pmaxird及额定输出限制Pref1后的限幅包络线相一致。因此,可认为该限幅包络线上U1、U2处所对应的点即本文第1节中所要探索的非线性拐点;故障后稳态有功输出特性由有功限幅PmaxP、转子电流限幅Pmaxird及额定输出限制Pref1确定。
进一步,可得限幅包络线数学表达式如下:
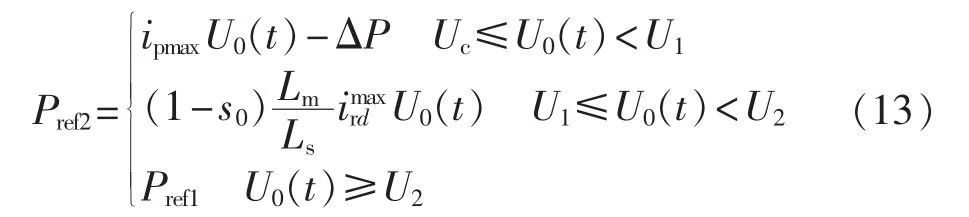
其中,Uc为触发Crowbar装置投入所对应的故障中稳态机端电压值;U1为有功功率限幅与转子电流限幅曲线相交处的机端电压值;U2为使有功功率以额定值输出的最小机端电压值。
式(13)反映了限幅环节和故障中稳态电压U0对DFIG故障中稳态有功功率输出的影响机理。即:当Uc≤U0<U1时,有功输出由有功限幅环节决定,即为图9中限幅包络线的a段;当U1≤U0<U2时,有功输出由转子电流限幅环节决定,即为图9中限幅包络线的b段;当U0≥U2时,有功输出为额定有功输出,即为图9中限幅包络线的c段。
5 结论
本文研究了在不同严重程度的三相对称故障下,限幅环节对DFIG故障中输出特性,特别是稳态有功输出特性的影响机理。其主要影响如下。
a.故障过程中,限幅环节可以有效减少Crowbar装置的投切次数,减少风电机组吸收的无功功率,同时抑制功率输出的波动。
b.在不触发Crowbar装置的情形下,DFIG故障中的稳态有功输出和稳态机端电压近似呈三段折线关系,分别由功率控制模块中的有功功率限幅环节、转子电流限幅环节和额定有功功率决定。
c.对于严重程度不同的故障,风机的有功输出特性不同。当故障较轻时,DFIG通过功率控制保持其额定有功输出;当故障程度加重时,DFIG稳态有功输出受转子电流限幅环节约束;当故障程度进一步加重时,DFIG稳态有功输出受有功功率限幅环节约束;当故障很严重时,会引起Crowbar投入,DFIG的控制环节被屏蔽,风机运行在类异步机模式。
研究揭示了在不同严重程度的故障下,DFIG故障中功率输出受到不同限幅环节影响的机理,可为更准确地描述DFIG暂态特性、为含风电的电力系统建模及相关的故障分析与控制提供理论参考。
另一方面,本文研究含诸多假设,且未考虑风机厂商控制策略和限幅环节的不同。因此,针对不同型号的风机,仍需进一步研究其限幅环节对风机输出的影响。
参考文献:
[1]AKHMATOV V.风力发电用感应发电机[M].本书翻译组,译.北京:中国电力出版社,2009:1-10.
[2]贺益康,胡家兵,Lie XU.并网双馈异步风力发电机运行控制[M].北京:中国电力出版社,2011:2-13.
[3]张保会,李光辉,王进,等.风电接入电力系统故障电流的影响因素分析及对继电保护的影响[J].电力自动化设备,2012,32(2):1-8.ZHANG Baohui,LI Guanghui,WANG Jin,et al.Affecting factors of grid-connected wind power on fault current and impact on protection relay[J].Electric Power Automation Equipment,2012,32(2):1-8.
[4]蒋长江,刘俊勇,刘友波,等.计及风电随机激励的电力系统暂态稳定分析[J].电力自动化设备,2016,36(3):100-108.JIANG Changjiang,LIU Junyong,LIU Youbo,etal.Transient stability analysis of power system considering wind-power stochastic excitation[J].Electric Power Automation Equipment,2016,36(3):100-108.
[5]金海峰,吴涛.风电接入系统后的电压稳定问题[J].电力自动化设备,2010,30(9):82-84.JIN Haifeng,WU Tao.Voltage stability after grid-connection of wind farm[J].Electric Power Automation Equipment,2010,30(9):82-84.
[6]ELLIS A,MULJADIE.Wind powerplantrepresentation in large-scale power flow simulations in WECC[C]∥Power and Energy Society GeneralMeeting-Conversion and Delivery of Electrical Energy in the 21st Century.Pittsburgh,USA:IEEE,2008:1-6.
[7]ELLIS A,POURBEIK P,SANCHEZ-GASCa J J,et al.Generic wind turbine generator models for WECC-a second status report[C]∥Power&Energy Society General Meeting.Denver,USA:IEEE,2015:1-5.
[8]张保会,李光辉,王进,等.风电接入对继电保护的影响(二)——双馈式风电场电磁暂态等值建模研究[J].电力自动化设备,2013,33(2):1-7.ZHANG Baohui,LI Guanghui,WANG Jin,et al.Impact of wind farm integration on relay protection(2):DFIG-based wind farm electromagnetic transient equivalent model[J].Electric Power Automation Equipment,2013,33(2):1-7.
[9]张文娟,马浩淼,张国慨,等.基于转子串联电阻的双馈风力发电机低电压穿越[J].电力自动化设备,2015,35(12):28-33.ZHANG Wenjuan,MA Haomiao,ZHANG Guokai,et al.Low voltage ride-through of doubly-fed induction generator based on rotor series resistor[J].Electric Power Automation Equipment,2015,35(12):28-33.
[10]訾鹏,周孝信,安宁,等.提高双馈式风力发电机机电暂态模型Crowbar保护仿真精度的方法[J].中国电机工程学报,2015,35(6):1322-1328.ZIPeng,ZHOU Xiaoxin,AN Ning,etal.A methodofimproving the accuracy ofdoubly-fed wind generatorelectromechanical transient model with Crowbar protection [J].Proceedings of the CSEE,2015,35(6):1322-1328.
[11]顾卓远,汤涌,刘文焯,等.双馈风力发电机组的电磁暂态-机电暂态混合仿真研究[J].电网技术,2015,39(3):615-620.GU Zhuoyuan,TANG Yong,LIU Wenzhuo,et al.Electromechanicaltransient-electromagnetic transienthybrid simulation of doubly-fed induction generator[J].Power System Technology,2015,39(3):615-620.
[12]赵卓立,杨苹,蔡泽祥,等.含风电孤立中压微电网暂态电压稳定协同控制策略[J].电力自动化设备,2015,35(10):1-9.ZHAO Zhuoli,YANG Ping,CAIZexiang,etal.Cooperative control of transient voltage stability for islanded medium-voltage microgrid with wind power[J].Electric Power Automation Equipment,2015,35(10):1-9
[13]侯俊贤,陶向宇,张静,等.基于低电压穿越控制策略的风电场等值方法[J].电网技术,2015,39(5):1281-1286.HOU Junxian,TAO Xiangyu,ZHANG Jing,et al.A low-voltage ride-through control strategy based equivalence method for wind farms[J].Power System Technology,2015,39(5):1281-1286.
[14]陈波,吴政球.基于约束因子限幅控制的双馈感应发电机有功功率平滑控制[J].中国电机工程学报,2011,31(27):130-137.CHEN Bo,WU Zhengqiu.Power smoothing control strategy of doubly-fed induction generator based on constraint factor extent-limit control[J].Proceedings of the CSEE,2011,31(27):130-137.
[15]HISKENS I A.Dynamics of type-3 wind turbine generator models[J].IEEE Transactions on Power Systems,2012,27(1):465-474.
[16]李治艳.双馈风力发电机降阶模型研究[D].北京:华北电力大学,2014.LI Zhiyan.The study of reduced order model for doubly-fed wind power generator[D].Beijing:North China Electric Power University,2014.
[17]丘晓明,赵斌,王玲玲,等.不对称电压跌落下双馈风电机组无功极限分析[J].可再生能源,2013,31(6):43-46.QIU Xiaoming,ZHAO Bin,WANG Lingling,et al.Reactive power capabilityanalysisofdoubly-fed induction generatorsunder unbalanced grid voltage drop conditions[J].Renewable Energy,2013,31(6):43-46.
[18]汪万伟,尹华杰,管霖.双闭环矢量控制的电压型PWM整流器参数整定[J].电工技术学报,2010,25(2):67-72.WANG Wanwei,YIN Huajie,GUAN Lin.Parameter setting for double closed-loop vector controlofvoltage source PWM rectifier[J].Transactions of China Electrotechnical Society,2010,25(2):67-72.
[19]IEC.Wind turbines-part 27-1:electrical simulation models-wind turbines:IEC61400-27-1[S].[S.l.]:IEC,2015.

