结合序列分布概率的储能系统典型功率曲线提取方法
杨锡运 ,任 杰,李相俊 ,董德华,贾学翠
(1.华北电力大学 控制与计算机工程学院,北京 102206;2.中国电力科学研究院 新能源与储能运行控制国家重点实验室,北京 100192)
0 引言
光伏发电受太阳辐照强度和温度的影响,其输出功率具有随机性和波动性,光伏发电直接并网会给电网的运行带来一定冲击[1-3]。在发电侧配置储能系统,利用储能系统快速响应和动态调节能力,平抑光伏电站短时功率波动[4-6],提高光伏发电跟踪计划出力能力[7],可改善光伏发电的电能品质,增加电网对光伏发电的接纳能力。
目前,国内外虽有多个光储联合发电示范项目,但对储能系统的研究主要集中在储能出力的优化控制和最优容量配置等方面,在平滑光伏电站功率波动应用情形下,挖掘储能系统典型功率曲线的研究成果较少。储能系统典型功率曲线是对实际功率的概括与提炼,能够反映储能系统的充放电特征。基于典型功率曲线不仅能掌握储能系统运行工况特征,增加对储能出力的整体认知,还能分析储能容量配置与典型功率曲线的关联关系,解决容量的最优配置问题。
挖掘典型曲线在电力系统负荷曲线等研究中经常提及。文献[8]提出一种基于云模型的典型运行曲线挖掘算法。文献[9]从电力负荷曲线形态出发,提出基于云模型和模糊聚类的典型电力负荷曲线挖掘方法。文献[10]提出基于经典聚类算法的集成聚类算法,通过bootstrap重采样、划分聚类和层次聚类来提取典型负荷曲线。文献[11]将不同天气类型下光伏出力与对应负荷叠加,形成负荷-光伏等效负荷曲线。文献[12]提出基于因子分析和模糊聚类的工况构建方法,利用该方法得到典型工况曲线。
本文针对利用储能系统平抑光伏电站功率波动的应用背景,提出一种结合序列分布概率的储能系统典型功率曲线挖掘方法。该方法基于储能系统功率在纵向时序(若干天的同一时刻)的区间分布特性,采用基于Bloch球面的量子遗传算法,寻找所有分布概率大于阈值ε的分布概率区间及相应区间的特征功率值,根据特征功率值得到该时刻典型功率值,整合所有时刻典型功率值得到典型功率曲线。将典型天气类型聚类为4种,根据所提挖掘算法得到4种天气类型下的储能系统典型功率曲线,并从典型参数、分布情况、相关性等角度出发对典型功率曲线进行综合分析,分析结果验证了该方法的有效性。
1 不同天气类型下储能系统充放电功率特征
光伏发电具有波动性,为光伏电站配置储能系统,利用储能系统平抑光伏电站功率波动,能够增加光伏发电的可利用率。
某装机容量为30MW的光伏电站,在晴天、多云、阴天和雨雪4种不同天气类型下的光伏电站日输出功率曲线如图1所示。由图1可知,4种天气类型下光伏功率曲线呈现不同特征,且具有明显的差别。晴天时光伏电站输出功率较高,且变化比较平稳;多云时光伏电站具有较高的输出功率,但受到云层的影响波动剧烈;阴天和雨雪天光伏电站输出功率整体偏低,但阴天时光伏功率略高于雨雪天。
不同天气类型下光伏电站功率波动情况不同,进而使得储能系统功率曲线呈现不同特征。图1中示例的晴天和雨雪天光伏电站功率的分钟级波动率主要在2%以内,光伏功率波动较小,对储能系统出力要求不高;多云和阴天时光伏电站功率的分钟级波动率集中在[0,20%]区间内,远高于晴天和雨雪天情况,对储能系统出力的要求提高。在平滑光伏功率波动率应用场景下,采用基于斜率控制的平滑策略[3]来确定储能系统的功率,图2显示了4种典型天气类型下储能系统功率曲线。

图1 典型天气类型下光伏功率曲线Fig.1 PV power curves under typical weather patterns

图2 典型天气类型下储能系统功率曲线Fig.2 Energy storage system power curves under typical weather patterns
由图2可知,不同天气类型下储能系统功率曲线特征不同,晴天时储能系统基本不出力,储能系统功率在[-0.2,0.2]MW以内;雨雪天时储能系统功率主要集中在[-2.5,2.5]MW区间内,功率曲线幅值小且变化平缓;多云和阴天时储能系统功率在[-10,10]MW区间内波动,功率曲线幅值较大且波动剧烈。
上述分析表明,储能系统功率曲线随光伏电站功率波动的不同而呈现不同运行特征,仅提取一条典型功率曲线难以表征不同天气下储能系统运行的特点,本文基于此提出一种结合序列分布概率的储能系统典型功率曲线挖掘方法:将储能系统众多运行曲线根据不同天气类型,聚类成晴天、多云、阴天和雨雪天四大类;用结合序列分布概率的挖掘方法提取4条不同天气类型下的典型功率曲线来表征储能系统的典型运行工况;并综合对比分析4条挖掘的功率曲线的信息,揭示储能系统运行特征。
2 储能系统典型功率曲线挖掘算法
2.1 储能系统典型功率曲线挖掘总体框图
挖掘4种天气类型下的储能系统典型功率曲线面临的主要问题是4种天气类型下储能系统功率数据的获取问题和典型功率值的挖掘问题。为解决上述问题,本文采用模糊C均值聚类方法[13]对光伏电站功率数据进行聚类,获得4种天气类型下的光伏功率数据;再采用文献[4]的平滑控制策略对光伏功率进行平滑,即可得到相应四大类的储能系统功率数据。基于获得的储能系统功率数据,提出基于序列分布概率的典型功率曲线挖掘算法获得储能系统的典型功率曲线。
图3给出了典型功率曲线挖掘总体流程图。

图3 储能系统典型功率曲线挖掘流程Fig.3 Flowchart of typical power curve mining for energy storage system
2.2 模糊C均值聚类
模糊C均值聚类算法聚类公式为:

其中,J(U,V)为目标函数;U为各数据点隶属度矩阵;μc(i)为第i个数据点相对于第c个聚类中心的隶属度;C 为聚类中心数;Xi(i=1,2,…,M)为聚类的第i个数据点,M为参与聚类的光伏电站数据天数;Vc为第c个聚类中心的位置向量;q为加权指数。
模糊C均值聚类算法对光伏电站数据进行聚类的步骤如下。
a.选取聚类特征。
本文将典型天气类型分为晴天、多云、阴天、雨雪天4种类型,即聚类中心数C=4。选取辐照度波动量、最大辐照比例、平均温度作为聚类特征,即:

其中,Vi为第i日辐照度波动量;Ki为第i日最大辐照比例;Ti为第i日平均温度。
辐照度波动量Vi反映太阳能电池板实际受辐射波动情况,计算公式为:
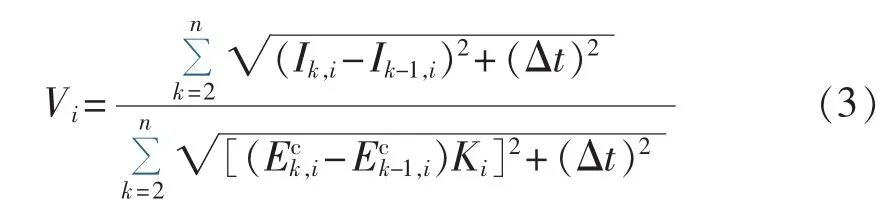
其中,n为辐照度数据采样点数;Ik,i为第i日第k个数据点的地表水平面实际辐照度;为第i日第k个数据点的地外水平面最大辐照度;Δt为辐照度数据点时间间隔。
最大辐照比例Ki是太阳能电池板接受到的实际太阳辐照度Ii与同时间段地外水平面最大辐照度的比值,计算公式为:

b.初始化各数据点隶属度矩阵U。
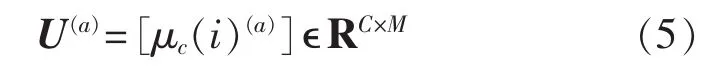
c.计算第a+1次迭代的聚类c的中心位置向量。

d.更新各数据点Xi的隶属度:

其中,b=1,2,…,C。
e.判断迭代结束条件。
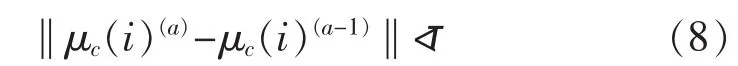
其中,τ为判断聚类终止条件的阈值。
采用文献[3]的平滑控制策略对聚类后的光伏电站功率数据进行平滑,即可得到相应四大类的储能系统功率数据。
2.3 基于序列分布概率的典型功率曲线挖掘算法
2.3.1 基于序列分布概率的典型功率曲线挖掘算法基本思想
从储能系统分散的功率数据挖掘典型功率曲线的挖掘算法主要思想可概括为:
a.针对某一时刻k,从不同天储能系统功率中,挖掘最能反映该时刻充放电特征的典型功率值Pk;
b.挖掘并整合所有时刻的典型功率值,得到储能系统典型功率曲线 Ptypical=[P1,P2,…,Pn]。
上述挖掘思想中,一个关键问题是如何从凌乱的储能数据中挖掘出k时刻能够代表储能系统充放电特征的典型功率值Pk。由于不同天同一k采样时刻的储能功率历史数据非常分散,本文利用储能系统功率在纵向时序的频率分布特性,提出采用基于Bloch球面的量子遗传算法,首先寻找大于设定阈值ε的最大分布概率区间,该区间具有聚集更多功率点的特征;然后再利用Bloch球面的量子遗传算法寻找各分布区间相应的特征功率值;最后结合特征功率值的概率信息得到k时刻典型功率值。
2.3.2 基于Bloch球面的量子遗传算法的寻优流程
如何优化找到最大分布概率区间Lopt1及相对应的特征功率值Ek1是算法的难点。遗传算法能够解决无梯度信息的优化问题。但传统遗传算法一般采用二进制编码,使得基因状态单一,容易发生陷入局部最优问题[14]。Bloch球面的量子遗传算法采用量子位编码形式,带来了种群多样性,为获得更好的优化效果,本文采用基于Bloch球面的量子遗传算法,针对目标函数,寻找储能系统功率值的最大分布概率区间Lopt1及相应特征功率值Ek1。
设m天内k时刻的储能系统历史数据构成的纵向功率向量为 Pk1= [p1k,p2k,…,pmk]T。从向量 Pk1中寻找功率值pgk分布最为集中的区间,作为最大分布概率区间 Lopt1=[xopt1,xopt1+d],区间长度 d 可根据储能系统最大功率值确定,本文选取区间长度d为储能系统最大功率值的10%。采用基于Bloch球面的量子遗传算法,寻找最大分布概率区间下限xopt1值。
定义优化目标函数J为:
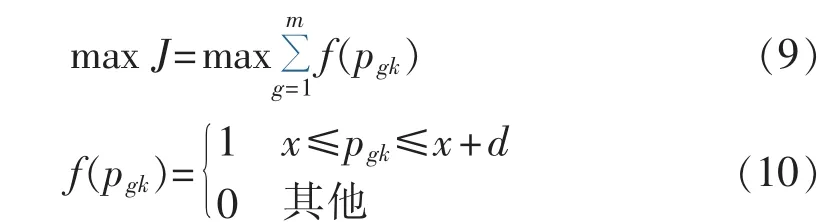
在Bloch球面的量子遗传算法中,区间下限x的编码表示为:

其中,i=1,2,…,S,S 为种群规模。
寻优过程中,x 的取值区间为[pmin,pmax],pmax为向量Pk1最大值,pmin为向量Pk1最小值。使用量子旋转门对2个角度参量φi、θi进行更新,完成种群的选择、交叉操作,使用变异算子完成种群的变异操作。同时引入灾变思想,增加量子非门操作,引导跳出局部最优[15]。
xopt1的具体优化流程可描述如下。
a.设定算法相关参数,种群规模为S,最大迭代次数为rmax。令迭代次数r=1,采用Bloch球面坐标对x值进行编码,随机产生角度参量φi和θi,得到初始化种群 Y(t)。
b.根据x的取值范围,对种群中个体进行反归一化处理,得到各变量值。
c.根据式(9)评价每个个体适应度,记录个体最优适应度和对应参数 φi、θi。
d.令迭代次数r=r+1,采用量子旋转门对角度参量 φi、θi进行更新,完成种群的选择、交叉操作,采用变异算子完成种群的变异操作,得到新一代种群Y(r)。
e.对新一代种群中个体进行反归一化处理,重新评价个体适应度,更新个体最优适应度和对应参数 φi、θi。
f.当最优个体长期不变时,对种群进行灾变处理,增加种群变异率。
g.若达到最大迭代次数,则搜索停止,输出xopt1寻优结果,否则转步骤d。
提取Pk1中落在最大概率区间Lopt1内的功率值,组成向量 Ik1= [p′1k,p′2k,…,p′tk]T,设向量 Ik1的最大值为 p′max,最小值为 p′min,在区间[p′min,p′max]内选取特征功率值Ek1,选取的原则为Ek1到向量Ik1中其他元素的欧氏距离最短。该区间的最优特征功率值Ek1获得同样采用基于Bloch球面的量子遗传算法寻优。算法寻优过程与区间下限xopt1的步骤相似,这里不再详述。但是需注意的是,此时Ek1的取值区间为[p′min,p′max],寻优的目标函数 T 定义为:
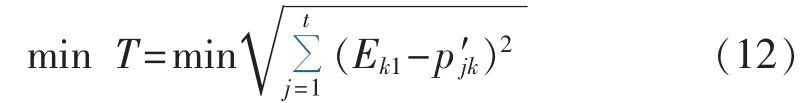
2.3.3 典型功率曲线挖掘算法流程
基于序列分布概率的典型功率曲线挖掘算法具体步骤可描述如下。
a.读取m天储能系统功率数据,组成功率值矩阵 H,矩阵中元素 pgk(g=1,2,…,m)为第g天k时刻储能系统功率。

b.提取m天内k时刻储能系统功率向量:Pk1=[p1k,p2k,…,pmk]T。
c.从向量Pk1中寻找功率值pgk分布最为集中的区间,作为最大分布概率区间 Lopt1=[xopt1,xopt1+d]。采用基于Bloch球面的量子遗传算法确定最大分布概率区间下限xopt1值,详细过程可参见2.3.2节。
提取Pk1中落在最大概率区间Lopt1内的功率值,组成向量Ik1=[p′1k,p′2k,…,p′tk,]T,并计算分布概率Fk1。

图4(a)给出该步骤示意图。图4(a)显示了采用基于Bloch球面的量子遗传算法对k时刻10个功率值进行优化分析后,得到功率值分布最为集中的区间,该分布区间内共有4个功率值。
d.采用基于Bloch球面的量子遗传算法计算特征功率值Ek1,详见2.3.2节。
e.从向量Pk1中减去向量Ik1中的功率值,得到新的向量Pk2。参照步骤c,得到最大分布概率区间Lopt2和向量 Ik2,并计算分布概率 Fk2,如图4(b)所示。
f.若Fk2小于阈值ε,则k=k+1,即进入寻找下一时刻的典型功率值;若Fk2不小于阈值ε,则参照步骤d找出特征功率值Ek2。参照步骤c、d,找到所有h个特征功率值,直到Fki小于阈值ε。阈值ε的取值可根据功率值分布的离散程度确定,功率值分布较为分散时,可适当减小ε的取值,反之可适当增加ε的取值。
g.从 k 时刻的特征功率值向量[Ek1,Ek2,…,Ekh]中,应用赌轮盘原理按概率原则选出某个元素Eki作为储能系统在k时刻的典型功率值Pk,Pk取值为Eki的概率为:

h.依次计算各个时刻储能系统典型功率值,得到储能系统典型功率曲线 Ptypical=[P1,P2,…,Pn]。

图4 储能系统典型功率曲线挖掘示意图Fig.4 Schematic diagram of typical power curve mining for energy storage system
图5为挖掘部分具体流程图。
3 仿真分析
3.1 4种天气类型的典型功率曲线

图5 挖掘部分具体流程图Fig.5 Specific flowchart of mining part
本文利用储能系统平滑光伏电站功率波动,挖掘该应用背景下储能系统运行过程中的典型功率曲线。以某30 MW光伏电站实际输出功率为分析处理对象,时间跨度为1 a,数据采样间隔Δt=1 min。采用模糊C均值聚类方法对光伏电站功率数据进行聚类,得到晴天、多云、阴天、雨雪天4种典型天气类型下的光伏功率,根据平滑控制策略得到相应的储能系统功率数据,如图6所示。

图6 储能系统功率数据(部分数据)Fig.6 Power data of energy storage system(partial data)
图6数据表明,4种天气类型下储能系统出力差异很大。根据本文提出的挖掘方法,得到4种天气类型下储能系统的典型功率曲线如图7所示。从图7可知,晴天时典型功率曲线显示储能系统出力最小,在[-0.2,0.2]MW区间内,多云天气下典型功率曲线在[-10,10]MW区间内波动,阴天时典型功率曲线在[-5,5]MW区间内,雨雪天的典型功率曲线在[-2.5,2.5]MW区间内,且各种天气类型下的典型功率曲线特征不同。

图7 典型天气类型下储能系统典型功率曲线Fig.7 Typical power curves of energy storage system under typical weather patterns
3.2 典型功率曲线特征分析
3.2.1 充放电功率分布对比分析
为进一步反映提取的典型功率曲线中蕴含的充放电功率分布信息,统计4种天气类型下储能系统典型功率的概率分布,如图8所示。由于光伏电站在夜间和太阳辐照度较低时段输出功率为0,图8统计的数据时段为06:00—19:00。

图8 储能系统典型功率分布直方图及拟合曲线Fig.8 Histogram of typical power distribution and its fitting curve for energy storage system
图8显示,晴天时储能系统典型功率的概率密度拟合曲线在0值处集中,表明储能系统出力变化范围小,典型功率曲线波动最为平缓。多云天气下的概率密度拟合曲线覆盖范围最宽,拟合曲线向0值两侧拉伸,表明此种天气类型对储能系统出力的需要最大,功率波动剧烈。尽管储能系统典型功率波动区间覆盖了[-10,10]MW,但大数值功率所占频率不高,典型功率主要集中在[-5,5]MW区间内。阴天和雨雪天的典型功率曲线波动相对较为剧烈,阴天时典型功率概率密度曲线覆盖范围略宽于雨雪天,尽管阴天时典型功率波动范围为[-5,5]MW,雨雪天的典型功率波动范围为[-2.5,2.5]MW,但2种天气类型下的典型功率都主要集中在[-1.5,1.5]MW区间内。
3.2.2 典型工况参数对比
从充电电量、放电电量、最大充电功率、最大放电功率和最大功率变化率等工况参数出发,定量分析4种天气下典型功率曲线的特征,如表1所示。
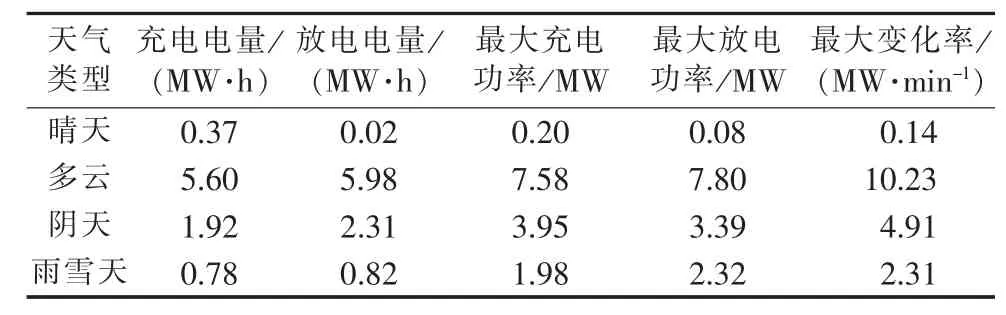
表1 典型功率曲线工况参数Table 1 Working parameters of typical power curves
由表1可知,在天气类型由晴天、雨雪天、阴天到多云的变化过程中,各个工况参数的数值不断增大,多云天气下典型功率曲线具有最大的充放电电量、最大充放电功率和最大功率变化率,代表储能系统运行过程中的最大充放电功率和最大使用容量信息,可进一步应用于储能系统的最优功率配置和容量配置,这也正是储能系统典型功率曲线挖掘的价值。
3.2.3 典型功率曲线相关性分析
以晴天时典型功率曲线为基准,引入纵向偏差[16]评价指标IR,分析晴天时典型功率曲线与不同天气类型下典型功率曲线的差别。
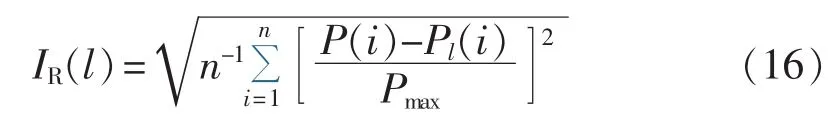
其中,IR(l)为晴天时典型功率曲线与第l种天气类型下典型功率曲线的纵向偏差;P为晴天时典型功率曲线;Pl为第l种天气类型下典型功率曲线;Pmax为典型功率曲线的最大值。
表2给出了晴天时典型功率曲线与不同天气类型下曲线的纵向偏差。由表2可知,晴天时典型功率曲线与多云天气下曲线的纵向偏差最大,与雨雪天气下的纵向偏差最小,但纵向偏差之间的差别较大。

表2 偏差评价指标IRTable 2 Deviation evaluation index IR
表3进一步给出了4种天气类型下典型功率曲线之间的相关系数。
由表3可知,不同天气类型下典型功率曲线之间的相关系数很小,曲线之间不存在相关性或相关性很低。表2和表3表明一条典型功率曲线难以表征不同天气下储能系统运行曲线的整体特点,提取不同天气类型下的典型功率曲线表征储能系统运行工况信息更具合理性。

表3 典型功率曲线的相关系数Table 3 Correlation coefficient of typical power curves
3.2.4 基于典型功率曲线的容量配置
利用提取的典型功率曲线,可以辅助解决储能系统容量的最优配置问题。由于不必再选用长时间跨度(例如1 a)的数据配置储能容量,具有压缩数据量、节省计算量的优点。
采用文献[17]容量配置计算公式:

其中,Cap为所配置的储能系统容量;Pi为典型功率曲线在 i时刻的充放电功率;1— m1、m2—m3、…、mn-1—mn为储能不间断充电/放电的数据采样时刻。
将典型功率曲线的数据代入式(17)—(19),计算得出所配置的储能系统容量如表4所示。

表4 基于典型功率曲线的容量配置Table 4 Capacity allocation based on typical power curves
表4表明,不同天气类型下配置的储能系统容量相差较大,其数值为储能系统的容量配置提供了参考。晴天时光伏电站输出功率波动率较低,对储能系统充放电要求不高,此时求出储能系统容量配置为0.32 MW·h;多云天气下光伏电站输出功率波动率较高,对储能系统出力要求高,此时求出储能系统容量配置为3.26 MW·h;阴天和雨雪天气下求出的储能系统容量配置介于晴天和多云之间。考虑到适应各种天气的容量配置需求,可采用多云天气下的3.26 MW·h作为光伏电站应配置的储能容量。
4 结论
本文提出了平滑光伏电站功率波动应用背景下的储能系统不同天气类型下典型功率曲线的挖掘方法,主要内容如下。
a.在分析不同天气类型下储能系统充放电功率特征不同的基础上,本文采用模糊C均值聚类方法对光伏电站功率数据进行聚类,获得不同天气类型下4类表征储能系统运行特征的充放电功率数据。
b.提出了一种基于纵向时序上概率分布特性的储能系统典型功率曲线的挖掘方法,利用储能系统功率分布概率信息挖掘典型功率曲线功率值。该方法基于Bloch球面的量子遗传算法,寻优得到储能功率的最大分布概率区间和特征功率值,依照概率信息挖掘出典型功率曲线。
c.根据挖掘算法得到4种天气类型下的储能系统典型功率曲线的典型参数、分布情况、相关性分析和容量配置表明,提取不同天气类型下的储能系统典型功率曲线表征储能系统运行工况信息更具合理性,对进一步应用于储能系统的最优功率配置和容量配置具有一定参考价值。
参考文献:
[1]丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报,2014,34(1):1-14.DING Ming,WANG Weisheng,WANG Xiuli,et al.A review on the effect of large-scale PV generation on power systems [J].Proceedings of the CSEE,2014,34(1):1-14.
[2]LI X,YAO L,HUI D.Optimal control and management of a large-scale battery energy storage system to mitigate fluctuation and intermittence of renewable generations[J].Journal of Modern Power Systems&Clean Energy,2016,4(4):593-603.
[3]陈炜,艾欣,吴涛,等.光伏并网发电系统对电网的影响研究综述[J].电力自动化设备,2013,33(2):26-32.CHEN Wei,AI Xin,WU Tao,et al.Influence of grid-connected photovoltaic system on power network[J].Electric Power Automation Equipment,2013,33(2):26-32.
[4]LI X,HUI D,LAI X.Battery Energy Storage Station(BESS)-based smoothing control of PhotoVoltaic(PV) and wind power generation fluctuations[J].IEEE Transactions on Sustainable Energy,2013,4(2):464-473.
[5]吕超贤,李欣然,户龙辉,等.基于小波分频与双层模糊控制的多类型储能系统平滑策略[J].电力系统自动化,2015,39(2):21-29.LÜ Chaoxian,LI Xinran,HU Longhui,et al.A smoothing strategy for hybrid energy storage system based on wavelet frequency allocation and two-level fuzzy control[J].Automation of Electric Power Systems,2015,39(2):21-29.
[6]吴振威,蒋小平,马会萌,等.用于混合储能平抑光伏波动的小波包-模糊控制[J].中国电机工程学报,2014,34(3):317-324.WU Zhenwei,JIANG Xiaoping,MA Huimeng,etal.Wavelet packet-fuzzy control of hybrid energy storage systems for PV power smoothing[J].Proceedings of the CSEE,2014,34(3):317-324.
[7]LI Q,CHOI S S,YUAN Y,et al.On the determination of battery energy storage capacity and short-term power dispatch of a wind farm[J].IEEE Transactions on Sustainable Energy,2011,2(2):148-158.
[8]韩晓娟,籍天明,李蓓,等.确定应用场景下的储能系统典型运行曲线挖掘[J].中国电机工程学报,2016,36(4):978-985.HAN Xiaojuan,JI Tianming,LI Bei,et al.Typical operation curve mining of energy storage system oriented to specific application scenario[J].Proceedings of the CSEE,2016,36(4):978-985.
[9]宋易阳,李存斌,祁之强.基于云模型和模糊聚类的电力负荷模式提取方法[J].电网技术,2014,38(12):3378-3383.SONG Yiyang,LI Cunbin,QI Zhiqiang.Extraction of power load patterns based on cloud model and fuzzy clustering[J].Power System Technology,2014,38(12):3378-3383.
[10]张斌,庄池杰,胡军,等.结合降维技术的电力负荷曲线集成聚类算法[J].中国电机工程学报,2015,35(15):3741-3749.ZHANG Bin,ZHUANG Chijie,HU Jun,et al.Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J].Proceedings of the CSEE,2015,35(15):3741-3749.
[11]陈禹,唐巍,陈昕玥,等.基于负荷-光伏等效负荷曲线动态分段的配电线路联络开关优化配置[J].电力自动化设备,2015,35(3):47-53.CHEN Yu,TANG Wei,CHEN Xinyue,etal.Tie switch allocation optimization based on dynamic segment of equivalent load-PV curve[J].Electric Power Automation Equipment,2015,35(3):47-53.
[12]石琴,郑与波.因子分析在汽车行驶工况构建过程中的应用[J].中国机械工程,2011,22(9):1123-1127.SHIQin,ZHENG Yubo.Application offactoranalysisin driving cycle development[J].China Mechanical Engineering,2011,22(9):1123-1127.
[13]MOSADEGHY M,YAN R,SAHA T K.Impact of PV penetration level on the capacity value of South Australian wind farms[J].Renewable Energy,2016,85:1135-1142.
[14]马速良,马会萌,蒋小平,等.基于Bloch球面的量子遗传算法的混合储能系统容量配置[J].中国电机工程学报,2015,35(3):592-599.MA Suliang,MA Huimeng,JIANG Xiaoping,etal.Capacity configuration of the hybrid energy storage system based on Bloch spherical quantum genetic algorithm[J].Proceedings of the CSEE,2015,35(3):592-599.
[15]李盼池.基于量子位Bloch坐标的量子遗传算法及其应用[J].控制理论与应用,2008,25(6):985-989.LI Panchi.Quantum genetic algorithm based on Bloch coordinates of qubits and its application[J].Control Theory&Applications,2008,25(6):985-989.
[16]徐曼,乔颖,鲁宗相.短期风电功率预测误差综合评价方法[J].电力系统自动化,2011,35(12):20-26.XU Man,QIAO Ying,LU Zongxiang.A comprehensiveerror evaluation method forshort-term wind powerprediction[J].Automation of Electric Power Systems,2011,35(12):20-26.
[17]修晓青,李建林,惠东.用于电网削峰填谷的储能系统容量配置及经济性评估[J].电力建设,2013,34(2):1-5.XIU Xiaoqing,LI Jianlin,HUI Dong.Capacity configuration and economic evaluation of energy storage system for grid peak load shifting[J].Electric Power Construction,2013,34(2):1-5.

